https://github.com/DedalusProject/dedalus
A flexible framework for solving PDEs with modern spectral methods.
https://github.com/DedalusProject/dedalus
fluid-dynamics pde-solver spectral-methods
Last synced: about 1 month ago
JSON representation
A flexible framework for solving PDEs with modern spectral methods.
- Host: GitHub
- URL: https://github.com/DedalusProject/dedalus
- Owner: DedalusProject
- License: gpl-3.0
- Created: 2020-05-16T19:02:11.000Z (almost 5 years ago)
- Default Branch: master
- Last Pushed: 2024-09-07T18:34:50.000Z (7 months ago)
- Last Synced: 2024-09-25T23:41:37.208Z (7 months ago)
- Topics: fluid-dynamics, pde-solver, spectral-methods
- Language: Python
- Homepage: http://dedalus-project.org/
- Size: 59.2 MB
- Stars: 495
- Watchers: 20
- Forks: 117
- Open Issues: 51
-
Metadata Files:
- Readme: README.md
- License: LICENSE.txt
- Citation: CITATION.cff
Awesome Lists containing this project
- awesome-fluid-dynamics - DedalusProject/dedalus - A flexible framework for solving PDEs with modern spectral methods.  [](https://github.com/DedalusProject/dedalus/search?l=jupyter-notebook) (Computational Fluid Dynamics / Spectral Methods)
- awesome-scientific-computing - GitHub
- awesome-sciml - DedalusProject/dedalus: A flexible framework for solving PDEs with modern spectral methods.
README
Dedalus Project
Dedalus is a flexible framework for solving partial differential equations using modern spectral methods.
The code is open-source and developed by a team of researchers studying astrophysical, geophysical, and biological fluid dynamics.
Dedalus is written primarily in Python and features an easy-to-use interface with symbolic vectorial equation specification.
For example, to simulate incompressible hydrodynamics in a ball, you can symbolically enter the equations, including [gauge conditions](https://dedalus-project.readthedocs.io/en/latest/pages/gauge_conditions.html) and [boundary conditions enforced with the tau method](https://dedalus-project.readthedocs.io/en/latest/pages/tau_method.html), as:
```python
problem.add_equation("div(u) + tau_p = 0")
problem.add_equation("dt(u) - nu*lap(u) + grad(p) + lift(tau_u) = - u@grad(u)")
problem.add_equation("u(r=1) = 0")
problem.add_equation("integ(p) = 0")
```
Our numerical algorithms produce sparse and spectrally accurate discretizations of PDEs on simple domains, including Cartesian domains of any dimension, disks, annuli, spheres, spherical shells, and balls:
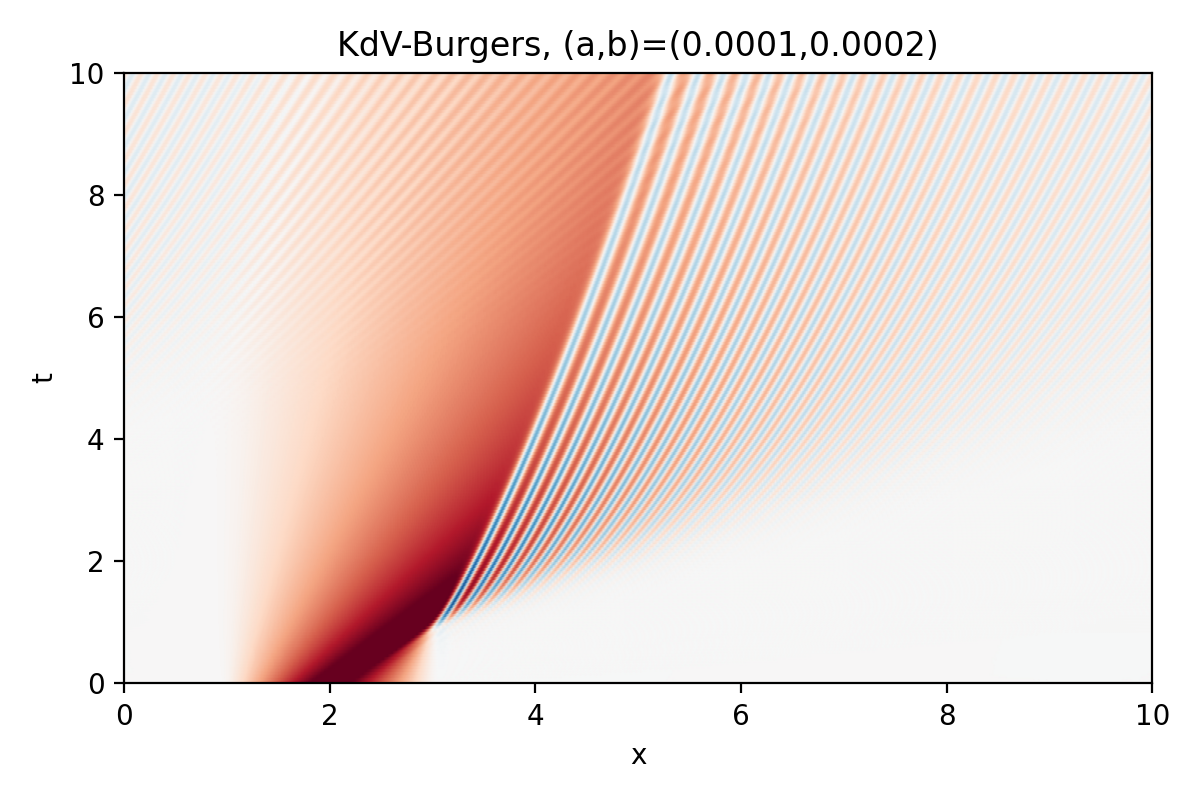
KdV-Burgers equation (1D IVP)
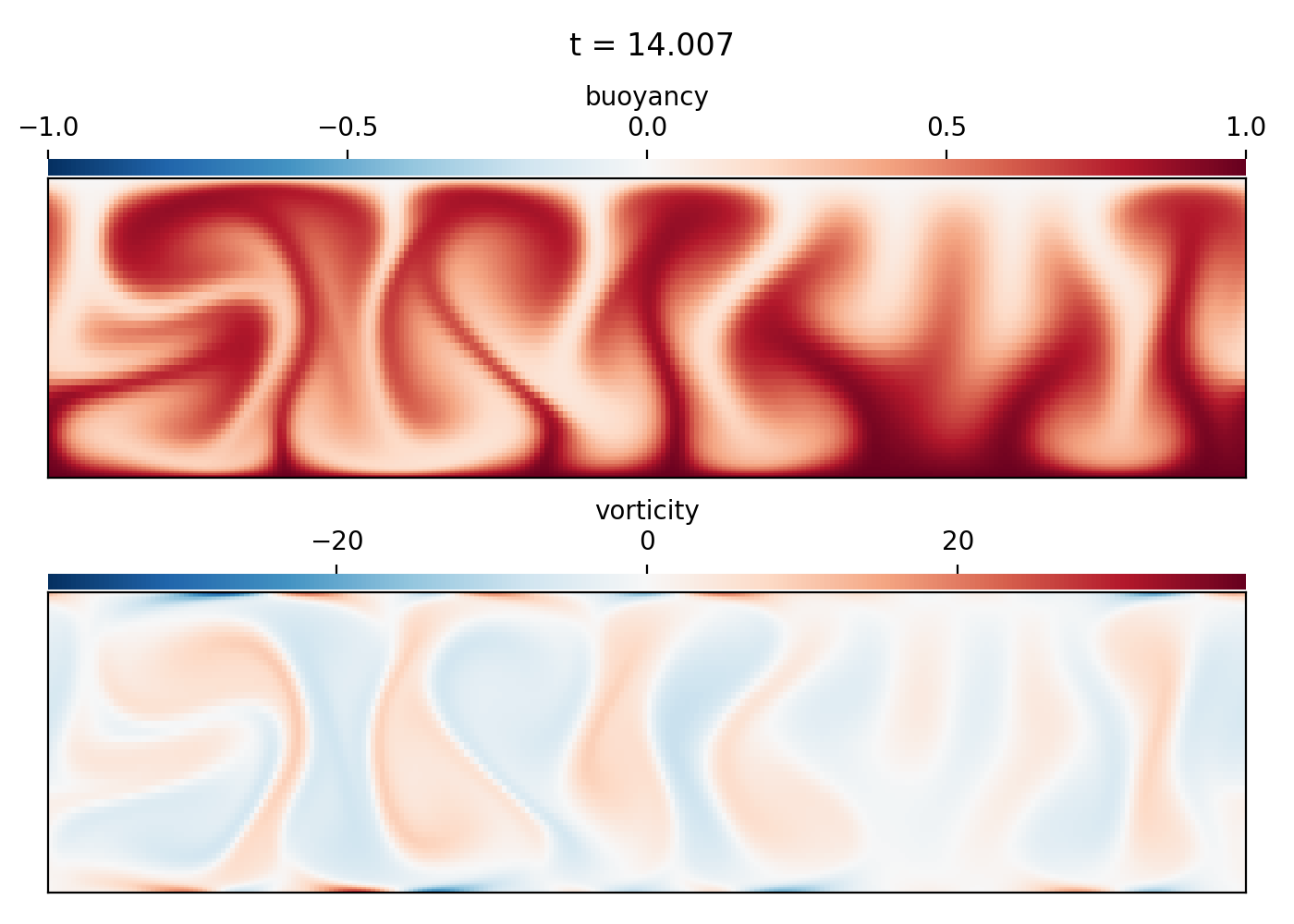
Rayleigh-Benard convection (2D IVP)
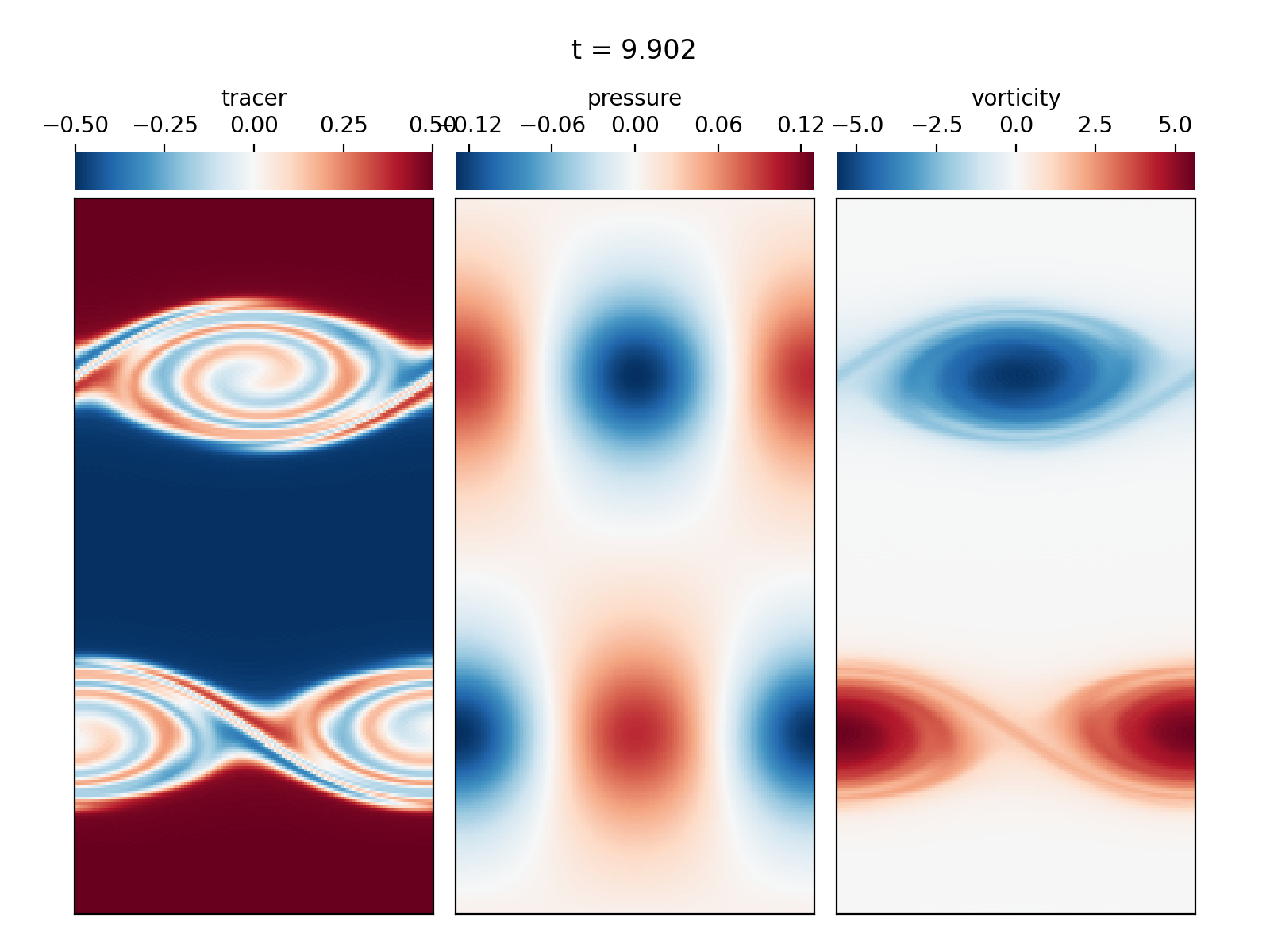
Periodic shear flow (2D IVP)
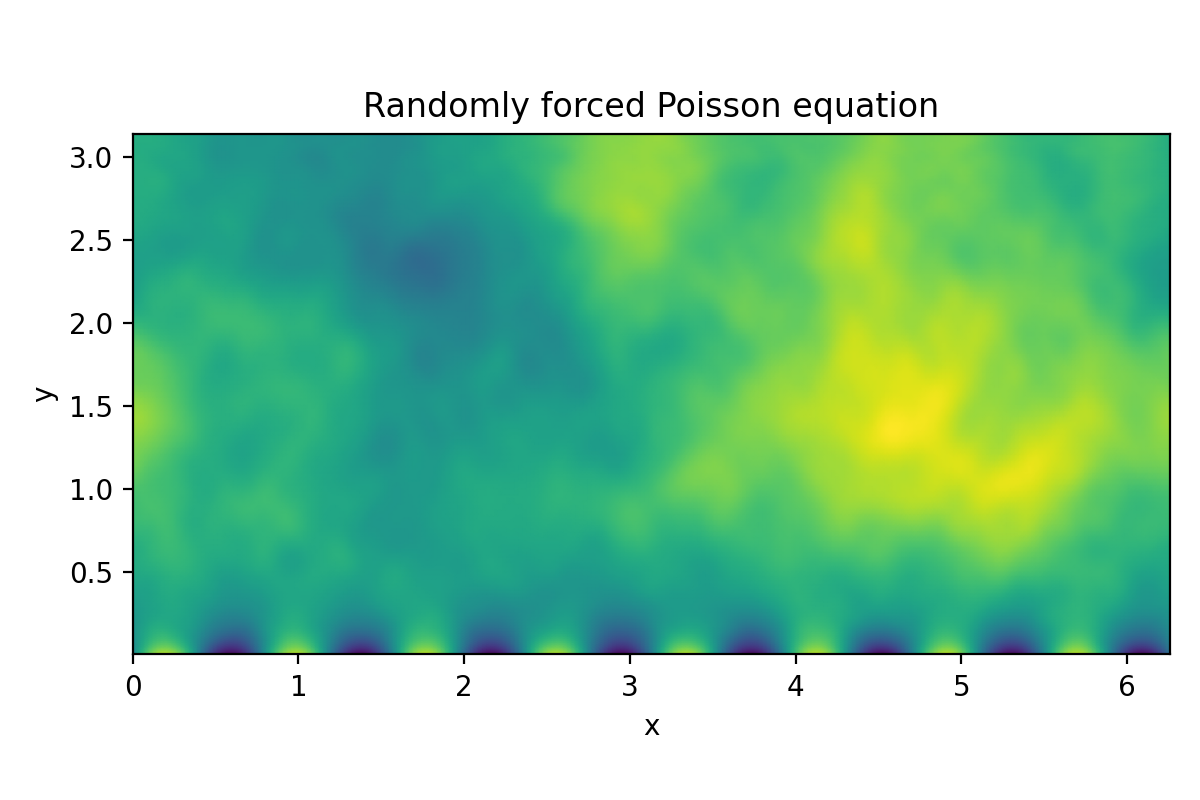
Poisson equation (2D LBVP)
Librational instability (disk IVP)
Spherical shallow water (sphere IVP)
Spherical shell convection (shell IVP)
Internally heated convection (ball IVP)
The resulting systems are efficiently solved using compiled libraries and are automatically parallelized using MPI.
See the [documentation](http://dedalus-project.readthedocs.org) for tutorials and additional examples.
## Links
* Project homepage:
* Code repository:
* Documentation:
* Mailing list:
## Developers
* [Keaton Burns (@kburns)](https://github.com/kburns)
* [Geoff Vasil (@geoffvasil)](https://github.com/geoffvasil)
* [Jeff Oishi (@jsoishi)](https://github.com/jsoishi)
* [Daniel Lecoanet (@lecoanet)](https://github.com/lecoanet/)
* [Ben Brown (@bpbrown)](https://github.com/bpbrown)