Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/JeremyBYU/FastGaussianAccumulator

Performs Gaussian Integration
https://github.com/JeremyBYU/FastGaussianAccumulator

Last synced: about 2 months ago
JSON representation

Performs Gaussian Integration

Awesome Lists containing this project

README 

        
# Fast Gaussian Accumulator



[![PyPI](https://img.shields.io/pypi/v/fastgac.svg)](https://pypi.org/project/fastgac/)

[![Docs](https://img.shields.io/badge/API-docs-blue)](https://jeremybyu.github.io/FastGaussianAccumulator/)

[![Run Tests](https://github.com/JeremyBYU/FastGaussianAccumulator/actions/workflows/tests.yml/badge.svg)](https://github.com/JeremyBYU/FastGaussianAccumulator/actions/workflows/tests.yml)

[![License](https://img.shields.io/pypi/l/fastgac.svg)](https://github.com/JeremyBYU/FastGaussianAccumulator/blob/master/LICENSE)



A Gaussian Sphere Accumulator refers to the notion of discretizing the **surface** of the unit sphere (a gaussian surface) into buckets/cells. One can then integrate/accumulate a list of **unit normals** into these buckets.

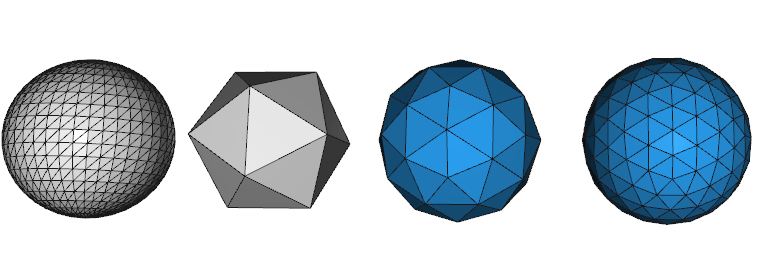
The end result is then a histogram of the sphere. There are many choices for the discretization process, however this library uses equilateral triangles because each cell will have nearly the same **area** and **shape**. This process is done by recursively subdividing (called "refining") the primary faces of an icosahedron. The following image shows our discretization strategy. The first object discretizes a sphere with uniform spacing of phi/theta (note small cells at poles, this represenation is not used), the second object is an icosahedron, the third object is the first level of recursion for an icosahedron, the last object is the second level of recursion of an icosahedron.



![Icosahedron](https://raw.githubusercontent.com/JeremyBYU/FastGaussianAccumulator/master/assets/imgs/refined_icosahedron.png)



Once a level of refinement is chosen, one can then integrate the surface normals of 3D triangular mesh into the cells/buckets. For example integrating the normals into a level four (4) icosahedron would look like the image below. Bright yellow indicates more counts for the triangle cells. This is basically showing that the floor [0, 0, 1] and walls [0, +/-1, 0] are common. Documenation can be found [here](https://jeremybyu.github.io/FastGaussianAccumulator/).



GaussianAccumulator



## Integrating Normals into the Gaussian Accumulator



To integrate normals into the Gaussian Accumulator one must **find** the cell that corresponds to the normal. This is a search process that has been implemented in several fashions in this repo. The main ways are as follows:



* 3D KD Tree - Do a nearest neighbor search using a binary tree.

    - `GaussianAccumulatorKDPY` - One implementation using scipy kdtree.

    - `GaussianAccumulatorKD` One implementation uses C++ nanoflann.

* Global Index and Local Search - A 3D point is transformed to a unique integer id. The unique ids have the property that ids close to each other will be close to each other in 3D space. The closest id is found corresponding to a triangle cell. A local search of triangle neighbors is performed to find closest triangle cell to the point.

    - `GaussianAccumulatorOpt` - Works good on **only** on the top hemisphere. Projects 3D point to plane using Azimuth Equal Area projection. Convert 2D point to int32 index using Hilbert Curve. This implementation is severely limited and is not recommended.

    - `GaussianAccumulatorS2Beta` - Works on full sphere! Uses Googles S2 space filling curve (uint64). 3D point is projected to unit cube, assigned to a face of the cube, and then a Hilbert curve index is found for that cube face. This is recommended, and what I use.



Use GaussianAccumulatorS2Beta! Look at `python -m examples.python.run_normals`

## Peak Detection



There are two (2) peak detection methods used within this repository. The user can choose which one best suit their needs.



### 2D Image Peak Detection



This method basically unwraps the icosahedron as a 2D image in a very particular way as described by [Gauge Equivariant Convolutional Networks and the Icosahedral CNN]("https://arxiv.org/abs/1902.04615). This unwrapping is hardcoded and fixed once a refinement level is chosen so it is very fast. The library then uses a 2D peak detector algorithm followed up with agglomerative hierarchial clustering (AHC) to group similar peaks. All of this is user configurable.



### 1D Signal Peak Detection



This performs peak detection on the 1D thread following the hilbert curve. This produces more peaks which are actually near each other on S2 and are then grouped with AHC. This actually works pretty well, but I recommend to use the 2D Image Peak Detector.



## Installation



For python there are pre-built binary wheel on PyPI for Windows and Linux. You can install with `pip install fastgac`.



Below are instruction to build the C++ Package (and python package) manaully with CMake. Installation is entirely through CMake now. You must have CMake 3.14 or higher installed and a C++ compiler with C++ 14 or higher.



### For C++ Users



1. `mkdir cmake-build && cd cmake-build`. - create build folder directory 

2. `cmake ../ -DCMAKE_BUILD_TYPE=Release` . For windows also add `-DCMAKE_GENERATOR_PLATFORM=x64` 

3. `cmake --build . -j4 --config Release`  - Build FastGA



### For Python Users (Requires CMake)



1. Install [conda](https://conda.io/projects/conda/en/latest/) or create a python virtual environment ([Why?](https://medium.freecodecamp.org/why-you-need-python-environments-and-how-to-manage-them-with-conda-85f155f4353c)). I recommend conda for Windows users.

2. `pip install .`



If you want to run the examples then you need to install the following (from main directory):



1. `pip install -r dev-requirements.txt` 



### Build and Install Python Extension and C++



Here building is entirely in CMake. You will build C++ Library and Python extension manually with CMake Commands.



1. Install [conda](https://conda.io/projects/conda/en/latest/) or create a python virtual environment ([Why?](https://medium.freecodecamp.org/why-you-need-python-environments-and-how-to-manage-them-with-conda-85f155f4353c)). I recommend conda for Windows users.

2. `cd cmake-build && cmake --build . --target python-package --config Release -j$(nproc)` 

3. `cd lib/python_package &&  pip install -e .`



If you want to run the examples then you need to install the following (from main directory):



1. `pip install -r dev-requirements.txt` 



## Documentation



Please see [documentation website](https://jeremybyu.github.io/FastGaussianAccumulator/) for more details.



## Citation



To support our work please cite:



```

@Article{s20174819,

author = {Castagno, Jeremy and Atkins, Ella},

title = {Polylidar3D-Fast Polygon Extraction from 3D Data},

journal = {Sensors},

volume = {20},

year = {2020},

number = {17},

article-number = {4819},

url = {https://www.mdpi.com/1424-8220/20/17/4819},

issn = {1424-8220}

}

```