Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/JsonChao/Awesome-Algorithm-Study
从零到一构建算法核心知识地图,打通你的任督二脉~
https://github.com/JsonChao/Awesome-Algorithm-Study
List: Awesome-Algorithm-Study
Last synced: 1 day ago
JSON representation
从零到一构建算法核心知识地图,打通你的任督二脉~
- Host: GitHub
- URL: https://github.com/JsonChao/Awesome-Algorithm-Study
- Owner: JsonChao
- License: apache-2.0
- Created: 2020-01-18T10:26:39.000Z (almost 5 years ago)
- Default Branch: master
- Last Pushed: 2023-03-23T13:58:16.000Z (over 1 year ago)
- Last Synced: 2024-05-23T00:03:26.830Z (6 months ago)
- Language: Java
- Homepage:
- Size: 1.96 MB
- Stars: 135
- Watchers: 5
- Forks: 29
- Open Issues: 1
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# Awesome-Algorithm-Study
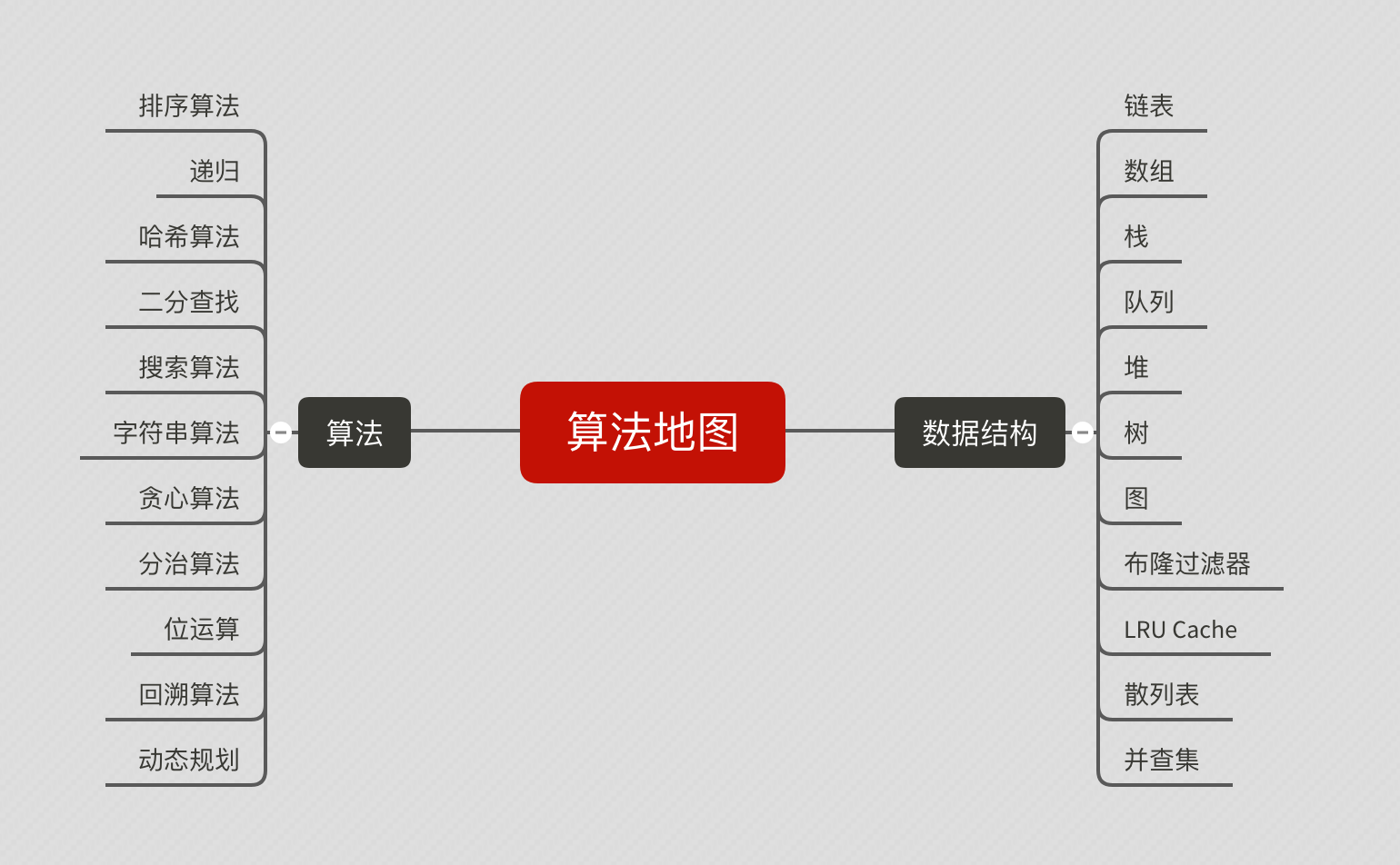
从零构建算法核心知识地图,打通你的任督二脉~
# 什么是算法面试?
- 1、不代表能够"正确"回答每一个算法问题,但是合理的思考方向其实更重要,也是正确完成算法面试的前提。
- 2、算法面试优秀并不意味着技术面试优秀,而技术面试优秀也并不意味着能够拿到 Offer。
- 3、把面试的过程看作是和面试官一起探讨一个问题的解决方案。对于问题的细节和应用场景,可以和面试官沟通。而这种沟通本身也是非常重要的,它暗示着你思考问题的方式。
- 4、如果是非常难的问题,对于你的竞争对手来说,也是难的。关键在于你所表达出的解决问题的思路。甚至通过表达解题思路的方向,得出结论:这个问题的解决方案,应该在哪一个领域,我们可以通过查阅或者进一步学习解决问题。例如:对于一组数据进行排序?思考:这组数据有什么特征?
- 1)、有没有可能包含有大量重复元素?如果有这种可能的话,三路快排是更好的选择。否则使用普通快排即可。
- 2)、是否大部分数据距离它正确的位置很近?是否近乎有序?如果是这样的话,插入排序是更好的选择。
- 3)、是否数据的取值范围非常有限?比如对学生成绩排序,如果是这样的话,计数排序是更好的选择。
- 4)、是否需要稳定的排序?如果是的话,归并排序是更好地选择。
- 5)、是否是使用链表存储的?如果是的话,归并排序是更好地选择,因为快排非常依赖于数组的随机访问。
- 6)、数据的大小是否可以装载到内存里?不能的话,需要使用外排序。
# 如何准备算法面试?
在学习和实践做题之间,要掌握平衡。
# 如何回答算法面试问题?
## 1、注意题目中的条件,例如
- 1)、给定一个有序的数组。
- 2)、设计一个 O(nlogn) 的算法。
- 3)、无需考虑额外的空间。
- 4)、数据规模大概是10000。
## 2、当没有思路时
- 1)、设计几个简单的测试用例,试验一下。
- 2)、不要忽视暴力解法。暴力解法通常是思考的起点。
## 3、优化算法
- 1)、遍历常见的算法思路。
- 2)、遍历常见的数据结构。
- 3)、空间和时间的交互(哈希表)。
## 4、预处理信息(排序)
## 5、在瓶颈处寻找答案:O(nlogn) + O(n^2)、O(n^3)
## 6、实际编写问题
- 1)、极端条件的判断:数组为空?字符串为空?数量为0?指针为 NULL?
- 2)、合理的变量名。
- 3)、注意代码的模块化、复用性。
## 7、面试答题四件套:
- 1、询问:题目细节、边界条件、可能的极端错误情况。
- 2、可能的解决方案:1)、时间 & 空间。2)、最优解。
- 3、编码。
- 4、测试用例。
# 时间复杂度
## 1、到底什么是大 O?
n 表示数据规模,O(f(n)) 表示运行算法所需要执行的指令数,和 f(n) 成正比。
## 2、数据规模的概念——如果想在1s之内解决问题
- 1)、O(n^2) 的算法可以处理大约10^4级别的数据。
- 2)、O(n) 的算法可以处理大约10^8级别的数据。
- 3)、O(nlogn) 的算法可以处理大约10^7级别的数据。
## 3、空间复杂度
- 1)、多开一个辅助的数组:O(n)。
- 2)、多开一个辅助的二维数组:O(n^2)。
- 3)、多开常数空间:O(1)。
- 4)、递归是有空间代价的,递归 n 次,空间复杂度就为 O(n)。
## 4、简单的时间复杂度分析
### 为什么要用大O,叫做大O(n)?
忽略了常数,实际时间 T = c1 * n + c2。
### 为甚不加上其中每一个常数项,而是要忽略它?
比如说把一个数组中的元素取出来这个操作,很有可能不同的语音基于不同的实现,它实际运行的时间是不等的。
就算转换成机器码,它对应的那个机器码的指令数也有可能是不同的。就算指令数是相同的,同样一个指令在 CPU
的底层,你使用的 CPU 不同,很有可能执行的操作也是不同的。所以,在实际上我们大概能说出来这个 c1
是多少,但是很难准确判断其具体的值。
大O的表示的是渐进时间复杂度,当 n 趋近于无穷大的时候,其算法谁快谁慢。
## 5、亲自试验自己算法的时间复杂度
O(log(n)) 与 O(n) 有着本质的差别。
## 6、递归算法的复杂度分析
- 1)、不是有递归的函数就是一定是 O(nlogn) 的。
- 2)、递归中进行一次递归调用:递归函数的时间复杂度为 O(T * depth)。
- 3)、递归中进行多次递归调用:画出递归树,计算调用次数。例如2次递归调用:2^0 + ... 2^n = 2^(n+1) - 1 = O(2^n)
- 4)、主定理:归纳了递归函数所计算时间复杂度的所有情况。
## 7、均摊时间复杂度分析(Amortized Time Analysis)与 避免复杂度的震荡
### 均摊时间复杂度分析
假设 capacity = n,n + 1 次 addLast/removeLast,触发 resize,总共进行 2n + 1 次基本操作平均来看,每次 addLast/removeLast 操作,进行 2 次基本操作均摊计算,时间复杂度为 O(1)。
### 复杂度震荡
当反复先后调用 addLast/removeLast 进行操作时,会不断地进行 扩容/缩容,此时时间复杂度为 O(n)出现问题的原因:removeLast 时 resize 过于着急。
解决方案:Lazy (在这里是 Lazy 缩容)等到 size == capacity / 4 时,才将 capacity 减半。
# 目录
## 一、排序算法
- 待排序的元素需要实现 Java 的 Comparable 接口,该接口有 compareTo() 方法,可以用它来判断两个元素的大小关系。
- 使用辅助函数 less() 和 swap() 来进行比较和交换的操作,使得代码的可读性和可移植性更好。
- 排序算法的成本模型是比较和交换的次数。
算法 | 稳定性 | 时间复杂度 | 空间复杂度 | 备注
---|---|---|---|---|
选择排序 | × | N2 | 1 |
冒泡排序 | √ | N2 | 1 |
插入排序 | √ | N ~ N2 | 1 | 时间复杂度和初始顺序有关
希尔排序 | × | N 的若干倍乘于递增序列的长度 | 1 | 改进版插入排序
快速排序 | × | NlogN | logN
三向切分快速排序 | × | N ~ NlogN | logN | 适用于有大量重复主键
归并排序 | √ | NlogN | N |
堆排序 | × | NlogN | 1 | 无法利用局部性原理 |
快速排序是最快的通用排序算法,它的内循环的指令很少,而且它还能利用缓存,因为它总是顺序地访问数据。它的运行时间近似为 ~cNlogN,这里的 c比其它线性对数级别的排序算法都要小。
使用三向切分快速排序,实际应用中可能出现的某些分布的输入能够达到线性级别,而其它排序算法仍然需要线性对数时间。
Java 主要排序方法为 java.util.Arrays.sort(),对于原始数据类型使用三向切分的快速排序,对于引用类型使用归并排序。
### Hot Question
- [**选择**](data_struct_study/src/sort_problem/Selection.java)
- [**冒泡**](data_struct_study/src/sort_problem/Bubble.java)
- [**插入**](data_struct_study/src/sort_problem/Insertion.java)
- [**希尔**](data_struct_study/src/sort_problem/Shell.java)
- [**归并**](data_struct_study/src/sort_problem/MergeSort.java)
- [**快速**](data_struct_study/src/sort_problem/QuickSort.java)
- [**三向切分快速**](data_struct_study/src/sort_problem/ThreeWayQuickSort.java)
- [**堆**](data_struct_study/src/sort_problem/HeapSort.java)
## 二、数组
数组最大的优点:快速查询,动态数组实现:
- 数组最好应用于"索引有语义"的情况(但并非所有有语义的索引都适用于数组,例如身份证号码)
- 我们需要额外处理索引有语义的情况
- 数组的容量:capacity,数组的大小:size,初始为0
- 1、实现基本功能:增删改查、各种判断方法等等
- 2、使用 泛型 让我们的数据结构可以放置 "任何"(不可以是基本数据类型,只能是类对象,好在每一个基本类型都有一个对应的包装类,它们之间可以自动进行装箱和拆箱的操作) 的数据类型
- 3、数组的扩容与缩容,手写时的易错点:
- 1、注意数组的下标
- 2、注意 size 与 capacity 的区别
### Hot Question
- [实现动态数组](data_struct_study/src/array/Array.java)
- [**二分搜索-1**](data_struct_study/src/array_problem/BinarySearch.java)
- [**二分搜索-2**](data_struct_study/src/array_problem/BinarySearch2.java)
- [**lengthOfLongestSubstring-1**](data_struct_study/src/array_problem/Solution3.java)
- [**lengthOfLongestSubstring-2**](data_struct_study/src/array_problem/Solution3_2.java)
- [**lengthOfLongestSubstring-3**](data_struct_study/src/array_problem/Solution3_3.java)
- [**lengthOfLongestSubstring-4**](data_struct_study/src/array_problem/Solution3_4.java)
- [**maxArea**](data_struct_study/src/array_problem/Solution11.java)
- [**合并区间**](data_struct_study/src/array_problem/Solution56.java)
- [**合并两个有序数组**](data_struct_study/src/array_problem/Solution88.java)
- [**findKthLargest**](data_struct_study/src/array_problem/Solution215.java)
- [**reverseRecursive**](data_struct_study/src/array_problem/Solution344.java)
- [**FindNumsAppearOnce**](data_struct_study/src/array_problem/Solution_1.java)
- [**数组中出现次数超过一半的数字**](data_struct_study/src/array_problem/Solution_2.java)
- [**数组中未出现的最小正整数字**](data_struct_study/src/array_problem/Solution_3.java)
- [longestPalindrome](data_struct_study/src/array_problem/Solution5.java)
- [search旋转排序数组](data_struct_study/src/array_problem/Solution33.java)
- [trap(接雨水)](data_struct_study/src/array_problem/Solution42.java)
- [sortColors-1](data_struct_study/src/array_problem/Solution75.java)
- [sortColors-2](data_struct_study/src/array_problem/Solution75_2.java)
- [longestConsecutive](data_struct_study/src/array_problem/Solution128.java)
- [twoSum-1](data_struct_study/src/array_problem/Solution167.java)
- [twoSum-2](data_struct_study/src/array_problem/Solution167_2.java)
- [twoSum-3](data_struct_study/src/array_problem/Solution167_3.java)
- [productExceptSelf](data_struct_study/src/array_problem/Solution238.java)
- [moveZeroes-1](data_struct_study/src/array_problem/Solution283.java)
- [moveZeroes-2](data_struct_study/src/array_problem/Solution283_2.java)
- [moveZeroes-3](data_struct_study/src/array_problem/Solution283_3.java)
- [moveZeroes-4](data_struct_study/src/array_problem/Solution283_4.java)
- [reverseVowels](data_struct_study/src/array_problem/Solution345.java)
- [findAnagrams](data_struct_study/src/array_problem/Solution438.java)
- [findCircleNNum](data_struct_study/src/array_problem/Solution547.java)
- [maxAreaOfIsland](data_struct_study/src/array_problem/Solution695.java)
## 三、队列
队列的基本应用 - 广度优先遍历
### Hot Question
- [实现ArrayQueue](data_struct_study/src/queue/ArrayQueue.java)
- [实现LoopQueue](data_struct_study/src/queue/LoopQueue.java)
- [**levelOrder**](data_struct_study/src/queue_problem/Solution102.java)
- [**二叉树的左视图**](data_struct_study/src/queue_problem/Solution199.java)
- [numSquares-1](data_struct_study/src/sort_problem/Solution279.java)
- [numSquares-2](data_struct_study/src/sort_problem/Solution279_2.java)
- [topKFrequent](data_struct_study/src/sort_problem/Solution347.java)
## 四、栈
栈的应用:
- 1)、无处不在的撤销操作
- 2)、系统栈的调用(操作系统)
- 3)、括号匹配(编译器)
### Hot Question
- [使用动态数组实现栈](data_struct_study/src/stack/ArrayStack.java)
- [**isValid**](data_struct_study/src/stack_problem/Solution20.java)
- [**inorderTraversal-1**](data_struct_study/src/stack_problem/Solution94.java)
- [**inorderTraversal-2**](data_struct_study/src/stack_problem/Solution94_2.java)
- [**preorderTraversal-1**](data_struct_study/src/stack_problem/Solution144.java)
- [**preorderTraversal-2**](data_struct_study/src/stack_problem/Solution144_2.java)
- [**postorderTraversal-1**](data_struct_study/src/stack_problem/Solution145.java)
- [**postorderTraversal-2**](data_struct_study/src/stack_problem/Solution145_2.java)
- [**最小值栈**](data_struct_study/src/stack_problem/Solution155.java)
- [**两个队列实现一个栈**](data_struct_study/src/stack_problem/Solution_1.java)
- [**表达式求值**](data_struct_study/src/stack_problem/Solution_2.java)
## 五、链表
> 链表,在节点间穿针引线。
为什么链表很重要?
- 不同于 动态数组、栈、队列的实现:其底层是依托静态数组,靠 resize 解决固定容量问题,
- 链表是真正的动态数据结构,也是最简单的动态数据结构。
- 能够帮助我们更深入地理解引用(指针)与递归。
- 优势:真正的动态,不需要处理固定容量的问题。
- 逆势:不同于数组其底层的数据是连续分布的,链表底层的数据分布是随机的,紧靠next(pre)指针连接,因此链表相对于数组丧失了随机访问的能力。
数组和链表的区别?
- 数组最好被应用于索引有语义的情况,例如 Students[1]。最大的优势:支持动态查询。
- 链表不能被应用于索引有语义的情况。最大的优势:动态。
链表的时间复杂度:
- 增: O(n)
- 删: O(n)
- 改: O(n)
- 查: O(n)
总结:链表不适合去修改,且只适合 增、删、查 链表头的元素,此时时间复杂度为 O(1)。
### Hot Question
- [实现链表](data_struct_study/src/LinkedList/LinkedList.java)
- [链表实现队列](data_struct_study/src/LinkedList/LinkedListQueue.java)
- [链表实现栈](data_struct_study/src/LinkedList/LinkedListStack.java)
- [**removeNthFromEnd-1**](data_struct_study/src/LinkedList_problem/Solution19.java)
- [**removeNthFromEnd-2**](data_struct_study/src/LinkedList_problem/Solution19_2.java)
- [**mergeTwoLists**](data_struct_study/src/LinkedList_problem/Solution21.java)
- [**mergeKLists**](data_struct_study/src/LinkedList_problem/Solution23.java)
- [**reverseKGroup**](data_struct_study/src/LinkedList_problem/Solution25.java)
- [**deleteDuplicates**](data_struct_study/src/LinkedList_problem/Solution83.java)
- [**hasCycle**](data_struct_study/src/LinkedList_problem/Solution141.java)
- [**detectCycle**](data_struct_study/src/LinkedList_problem/Solution142.java)
- [**reverseList-1**](data_struct_study/src/LinkedList_problem/Solution206.java)
- [**reverseList-2**](data_struct_study/src/LinkedList_problem/Solution206_2.java)
- [**addTwoNumbers**](data_struct_study/src/LinkedList_problem/Solution445.java)
- [**FindFirstCommonNode**](data_struct_study/src/LinkedList_problem/Solution_1.java)
- [**单链表的选择排序**](data_struct_study/src/LinkedList_problem/Solution_2.java)
- [**链表中倒数第k个节点**](data_struct_study/src/LinkedList_problem/Solution_3.java)
- [**判断一个链表是否为回文结构点**](data_struct_study/src/LinkedList_problem/Solution_4.java)
- [addTwoNumbers](data_struct_study/src/LinkedList_problem/Solution2.java)
- [swapPairs](data_struct_study/src/LinkedList_problem/Solution24.java)
- [sortList](data_struct_study/src/LinkedList_problem/Solution148.java)
- [getIntersectionNode](data_struct_study/src/LinkedList_problem/Solution160.java)
- [removeElements](data_struct_study/src/LinkedList_problem/Solution203.java)
- [isPalindrome](data_struct_study/src/LinkedList_problem/Solution234.java)
- [deleteNode](data_struct_study/src/LinkedList_problem/Solution237.java)
- [oddEvenList](data_struct_study/src/LinkedList_problem/Solution328.java)
## 六、哈希表
什么是哈希函数?
哈希函数:将 "键" 转换为 "索引",每一个 "键" 对应唯一的一个索引。
- 很难保证每一个 "键" 通过哈希函数的转换对应不同的 "索引",因此会产生哈希冲突。
- "键" 通过哈希函数得到的 "索引" 分布越均匀越好。
- 在哈希表(空间换时间)上操作,主要要考虑如何解决哈希冲突。
哈希函数的设计
通用的方法——转换为整形处理:
1、小范围正整数直接使用。
2、小范围负整数进行偏移。(-100~100 => 0~200)
3、大整数:通常做法——取模,例如对身份证号取模后6位,即取最后6位,
因为倒数第5、6位是表示1~31,所以会导致分布不均匀的情况。
一个简单的解决办法就是模一个素数,例如7.
素数取值表:http://planetmath.org/goodhashtableprimes
4、浮点型:在计算机中都是32位或64位的二进制表示,只不过计算机解析成了浮点数。我们可以直接将二进制转换为整形来处理。
5、字符串:
```Java
166 = 1 * 10^2 + 6 * 10^1 + 6 * 10^0
code = c * 26^3 + o * 26^2 + d * 26^1 + e * 26^0
code = c * B^3 + o * B^2 + d * B^1 + e * B^0
hash(code) = (c * B^3 + o * B^2 + d * B^1 + e * B^0) % M(素数)
降低计算量:
hash(code) = ((((c * B) + o) * B + d) * B) + e) % M
避免整形溢出:
hash(code) = ((((c % M) * B + o) % M * B + d) % M * B + e) % M
代码形式:
int hash = 0;
for(int i = 0;i < s.length();i++) {
hash = (hash * B + s.charAt(i)) % M;
}
```
6、复合类型:也是利用字符串的上述公式,例如 Date:year、month、day。
hash(code) = (((date.year % M) * B + date.month) % M * B + date.day) % M
设计原则:
- 1、一致性:如果 a == b,则 hash(a) == hash(b)
- 2、高效性:计算高效简便
- 3、均匀性:哈希值均匀分布
Java 中 Object 的 hashCode 是根据每一个对象的地址映射成整形。
哈希冲突的处理
1、链地址法(Separate Chaining):
- 去掉 k1 符号:(hashCode(k1) & 0x7fffffff) % M,& 0x7fffffff 表示将 k1 最高位变为0。
- HashMap 本质就是一个 TreeMap 数组。
- HashSet 本质就是一个 TreeSet 数组。
- Java8 之前,每一个位置对应一个链表,Java8 开始,当哈希冲突达到一定程度
(平均来讲,每一个位置存储的元素树多于某一个程度了),每一个位置从链表转成红黑树。
- HashMap 容量的选取非常重要,恰当的容量能够避免数组扩容和尽量减少 hash 冲突。
算法复杂度分析:
总共有 M 个地址,如果放入哈希表的元素为 N。
- 如果地址是链表:O(N/M)
- 如果地址是平衡树:O(log(N/M))
为了实现均摊复杂度 O(1),需要对哈希表进行动态空间处理,即
- 1、平均每个地址承载的元素多过一定程度,即扩容 N/M >= upperTol
- 2、平均每个地址承载的元素少过一定程度,即缩容 N/M < lowerTol
- 3、对于哈希表来说,元素树从 N 增加到 upperTol * N,地址空间翻倍
- 4、每个操作在 O(LOWER_TOL)~O(UPPER_TOL) => O(1)
更复杂的动态空间处理方法
扩容 M -> 2 * M => 不是素数
解决方案:使用素数取值表中的值:http://planetmath.org/goodhashtableprimes
哈希表相比 AVL、红黑树 而言,牺牲了顺序性,换来了更好的性能。
集合、映射:
- 1、有序集合(TreeSet)、有序映射(TreeMap):平衡树。
- 2、无序集合(HashSet)、无序映射(HashMap):哈希表。
更多的哈希冲突处理方法:
1、开发地址法(线性探测法):对于开放地址法来说,每一个地址就是直接存元素,
即每一个地址都对所有的元素是开放的。如果有冲突,直接存到当前索引的下一个索引对应的位置,
如果位置还被占用,继续往下寻找即可。
(平方探测法): +1、+4、+9、+16。
(二次哈希法):使用另外一个 hash 算法来计算出下一个位置要去哪儿,hash2(key)。
负载率(LoaderFactory):元素占总容量比,超过它就需要进行扩容,
一般选取为50%,选取合适时间复杂度可以到达 O(1)。
2、再哈希法(Rehashing):使用另外一个 hash 算法来计算出下一个位置要去哪儿。
3、Coalesced Hashing:综合了 Separate Chaining 和 Open Addressing。
两类查找问题:
- 1、查找有无:元素 a 是否存在?set;集合。
- 2、查找对应关系(键值对应):元素 a 出现了几次?map;字典。
常见操作:
- 1、insert
- 2、find
- 3、erase
- 4、change(map)
### Hot Question
- [实现哈希表](data_struct_study/src/hash_table/HashTable.java)
- [**twoSum-1**](data_struct_study/src/hash_table_problem/Solution1.java)
- [**twoSum-2**](data_struct_study/src/hash_table_problem/Solution1_2.java)
- [**threeSum**](data_struct_study/src/hash_table_problem/Solution15.java)
- [firstUniqChar](data_struct_study/src/hash_table/Solution1.java)
- [groupAnagrams](data_struct_study/src/hash_table_problem/Solution49.java)
- [isIsomorphic](data_struct_study/src/hash_table_problem/Solution205.java)
- [containsDuplicate](data_struct_study/src/hash_table_problem/Solution217.java)
- [containsNearbyDuplicate](data_struct_study/src/hash_table_problem/Solution219.java)
- [containsNearbyAlmostDuplicate](data_struct_study/src/hash_table_problem/Solution220.java)
- [isAnagram](data_struct_study/src/hash_table_problem/Solution242.java)
- [intersection-1](data_struct_study/src/hash_table_problem/Solution349.java)
- [intersection-2](data_struct_study/src/hash_table_problem/Solution_349_2.java)
- [intersect-1](data_struct_study/src/hash_table_problem/Solution350.java)
- [intersect-2](data_struct_study/src/hash_table_problem/Solution350_2.java)
- [numberOfBoomerangs](data_struct_study/src/hash_table_problem/Solution447.java)
- [frequencySort](data_struct_study/src/hash_table_problem/Solution451.java)
- [fourSumCount-1](data_struct_study/src/hash_table_problem/Solution454.java)
- [fourSumCount-2](data_struct_study/src/hash_table_problem/Solution454_2.java)
## 七、(二分搜索)树
树结构本身是一种天然的的组织结构,用树存储数据能更加高效地搜索。
二叉树:和链表一样,动态数据结构。二叉树天然的递归结构,空也是一颗二叉树。
- 1)、对于每一个节点,最多能分成2个节点,即左孩子和右孩子。
- 2)、没有孩子的节点称为叶子节点。
- 3)、每一个孩子节点最多只能有一个父亲节点。
- 4)、二叉树具有天然的递归结构,即每个节点的左右子树都是二叉树。
注意:一个节点也是二叉树、空也是二叉树。
满二叉树:除了叶子节点外,每个节点都有两个子节点。
二分搜索树:
- 1)、二分搜索树是一个二叉树,且其每一颗子树也是二分搜索树。
- 2)、二分搜索树的每个节点的值大于其左子树的所有节点的值,小于其右子树的所有节点的值。
- 3)、存储的元素必须有可比较性。
- 4)、通常来说,二分搜索树不包含重复元素。如果想包含重复元素的话,只需定义:
左子树小于等于节点;或者右子树大于等于节点。注意:数组和链表可以有重复元素。
什么是遍历操作?
- 1)、遍历就是把所有的节点都访问一遍。
- 2)、访问的原因和业务相关。
- 3)、在线性结构下,遍历是极其容易的,但是在树结构中,遍历会稍微有点难度。
如何对二叉树进行遍历?
对于遍历操作,两颗子树都要顾及。
- 前序遍历:最自然和常用的遍历方式。规律:根左右
- 中序遍历:规律:左根右
- 后序遍历:中序遍历的结果就是我们在二叉搜索树中所有数据排序后的结果。规律:左右根。应用:为二分搜索树释放内存。
心算出二叉搜索树的前中后序遍历:每一个二叉树都会被访问三次,从根节点出发,
- 前序遍历:当一个节点被访问第一次就记录它。
- 中序遍历:当一个节点被访问第二次的时候记录它。
- 后序遍历:当一个节点被访问第三次的时候才记录它。
前序遍历的非递归实现(深度优先遍历):需要使用栈记录下一步被访问的元素。
对于二叉搜索树的非递归实现一般有两种写法:
- 1)、经典教科书写法。
- 2)、完全模拟系统调用栈的写法。
层序遍历(广度优先遍历):需要使用队列记录当前出队元素的左右子节点。
广度优先遍历的意义:
- 1)、在于快速地查询要搜索的元素。
- 2)、更快地找到问题的解。
- 3)、常用于算法设计中——无权图最短路径。
- 4)、联想对比图的深度优先遍历与广度优先遍历。
从二分搜索树中删除最小值与最大值:往左走的最后一个节点即是存有最小值的节点,往右走的最后一个节点即是存有最大值的节点。
删除二分搜索树种的任意元素:
- 1)、删除只有左孩子的节点。
- 2)、删除只有右孩子的节点。
- 3)、删除具有左右孩子的节点:
1、找到 s = min(d->right),
s 是 d 的后继(successor)节点,也即 d 的右子树中的最小节点。
s->right = delMin(d->right),
s->left = d->left,
删除 d,s 是新的子树的根。
2、找到 p = max(d->left),
p 是 d 的前驱(predecessor)节点。
如何高效实现 rank(E 是排名第几的元素)?
如何高效实现 select(查找排名第10的元素)?
最好的方式是实现一个维护 size 的二分搜索树:给 Node 节点添加新的成员变量 size。
### Hot Question
- [实现二分搜索树](data_struct_study/src/binary_search_tree/BST.java)
- [实现 AVL 树](data_struct_study/src/avl/AVLTree.java)
- [实现红黑树](data_struct_study/src/red_black_tree/RBTree.java)
- [实现分段树](data_struct_study/src/segment_tree/SegmentTree.java)
- [实现前缀树](data_struct_study/src/trie)
- [实现并查集](data_struct_study/src/union_find)
- [**maxDepth**](data_struct_study/src/binary_search_tree_problem/Solution104.java)
- [**lowestCommonAncestor-1**](data_struct_study/src/binary_search_tree_problem/Solution235.java)
- [**lowestCommonAncestor-2**](data_struct_study/src/binary_search_tree_problem/Solution236.java)
- [**二叉树根节点到叶子节点的所有路径和**](data_struct_study/src/binary_search_tree_problem/Solution_1.java)
- [**二叉树的之字形遍历**](data_struct_study/src/binary_search_tree_problem/Solution_2.java)
- [isValidBST](data_struct_study/src/binary_search_tree_problem/Solution101.java)
- [isSymmetric](data_struct_study/src/binary_search_tree_problem/Solution101.java)
- [sortedArrayToBST](data_struct_study/src/binary_search_tree_problem/Solution108.java)
- [isBalanced](data_struct_study/src/binary_search_tree_problem/Solution110.java)
- [minDepth](data_struct_study/src/binary_search_tree_problem/Solution111.java)
- [hasPathSum](data_struct_study/src/binary_search_tree_problem/Solution112.java)
- [rob](data_struct_study/src/binary_search_tree_problem/Solution198_8.java)
- [invertTree](data_struct_study/src/binary_search_tree_problem/Solution226.java)
- [kthSmallest](data_struct_study/src/binary_search_tree_problem/Solution230.java)
- [binaryTreePaths](data_struct_study/src/binary_search_tree_problem/Solution257.java)
- [sumOfLeftLeaves](data_struct_study/src/binary_search_tree_problem/Solution404.java)
- [pathSum](data_struct_study/src/binary_search_tree_problem/Solution437.java)
## 八、映射
映射 Map
- 1)、存储 Key:value 数据对的数据结构。
- 2)、根据 Key,寻找 Value。
非常容易使用链表或者二分搜索树来实现。
LinkedListMap BSTMap 平均 最差
add、remove、set、get、contains O(n) O(h) O(logn) O(n)
### Hot Question
- [二分搜索树实现映射](data_struct_study/src/map/BSTMap.java)
- [链表实现映射](data_struct_study/src/map/Bubble.java)
- [intersect](data_struct_study/src/map/Solution1.java)
## 九、堆、优先队列
- 普通队列:先进先出,后进后出
- 优先队列:出队顺序和入队顺序无关,和优先级相关
应用场景:操作系统的任务调度,动态 选择优先级最高的任务进行处理。医生和患者之间的关系。
优先队列底层实现 | 入队 | 出队 |
---|---|---|
普通线性结构 | O(1) | O(n) |
顺序线性结构 | O(n) | O(n) |
堆 | O(logn) | O(logn) |
堆的基本结构
二叉堆:满足特殊性质的二叉树。
- 1、二叉堆是一颗完全二叉树,完全二叉树即把元素顺序一层一层地排列成树的形状。
- 2、堆中每一个元素的值都大于等于它的孩子节点。
用数组存储二叉树:
```Java
parent = (i - 1) / 2
leftNode = 2 * i + 1
rightNode = 2 * i + 2
```
### Hot Question
- [动态数组实现最大堆](data_struct_study/src/heap_and_priority_queue/MaxHeap.java)
- [最大堆实现优先队列](data_struct_study/src/heap_and_priority_queue/PriorityQueue.java)
- [**topKFrequent-1**](data_struct_study/src/heap_and_priority_queue/Solution.java)
- [**topKFrequent-2**](data_struct_study/src/heap_and_priority_queue/Solution2.java)
## 十、递归与回溯
递归:本质就是将原来的问题转换为更小的问题。
- 1)、注意递归函数的宏观语义。
- 2)、递归函数就是一个普通的函数,仅完成一个功能而已。
递归算法通常分为两步:
- 1)、求解基本问题。
- 2)、把原问题转化为更小的问题。
递归调用是有代价的:函数调用 + 系统栈空间
其它常见的链表类型:
- 1)、双向链表,每一个 ListNode 同时具有 pre、next 指针
- 2)、双向循环链表:能够更进一步地封装很多便利的操作,Java 中的 LinkedList 的本质就是双向循环链表。
- 3)、数组链表:如果明确知道要存储元素的总数,使用数组链表会更加方便,数组中存储一个个的 Node,Node 包含元素 e 与 int 型的 next 指针。
### Hot Question
- [**permute**](data_struct_study/src/backstracking_problem/Solution46.java)
- [**permuteUnique**](data_struct_study/src/backstracking_problem/Solution47.java)
- [removeElements-1](data_struct_study/src/recursion/Solution.java)
- [removeElements-2](data_struct_study/src/recursion/Solution2.java)
- [removeElements-3](data_struct_study/src/recursion/Solution3.java)
- [removeElements-4](data_struct_study/src/recursion/Solution4.java)
- [removeElements-5](data_struct_study/src/recursion/Solution.java)
- [letterCombinations](data_struct_study/src/backstracking_problem/Solution17.java)
- [generateParenthesis](data_struct_study/src/backstracking_problem/Solution22.java)
- [combinationSum](data_struct_study/src/backstracking_problem/Solution39.java)
- [combinationSum2](data_struct_study/src/backstracking_problem/Solution40.java)
- [solveNQueens](data_struct_study/src/backstracking_problem/Solution51.java)
- [combine](data_struct_study/src/backstracking_problem/Solution77.java)
- [combine-2](data_struct_study/src/backstracking_problem/Solution77_2.java)
- [subsets](data_struct_study/src/backstracking_problem/Solution78.java)
- [exist](data_struct_study/src/backstracking_problem/Solution79.java)
- [subsetsWithDup](data_struct_study/src/backstracking_problem/Solution90.java)
- [restoreIpAddresses](data_struct_study/src/backstracking_problem/Solution93.java)
- [floodfill](data_struct_study/src/backstracking_problem/Solution130.java)
- [partition](data_struct_study/src/backstracking_problem/Solution131.java)
- [numIslands](data_struct_study/src/backstracking_problem/Solution200.java)
- [combinationSum3](data_struct_study/src/backstracking_problem/Solution216.java)
## 十一、动态规划
什么是动态规划?
斐波那契数列——解决递归中的 重叠子问题 && 最优子结构:通过求子问题的最优解,可以获得原问题的最优解:
- 1、记忆化搜索避免重复运算,自上而下的解决问题。
- 2、动态规划,自下而上的解决问题。
动态规划将是将原问题拆解成若干个子问题,同时保存子问题的答案,使得每个子问题只求解一次,最终获得原问题的答案。
### Hot Question
- [背包问题](data_struct_study/src/dynamic_problem/Solution.java)
- [**climbStairs-1**](data_struct_study/src/dynamic_problem/Solution70.java)
- [**climbStairs-2**](data_struct_study/src/dynamic_problem/Solution70_2.java)
- [**climbStairs-3**](data_struct_study/src/dynamic_problem/Solution70_3.java)
- [**maxProfit_k_1**](data_struct_study/src/dynamic_problem/Solution121.java)
- [**maxProfit_k_inf**](data_struct_study/src/dynamic_problem/Solution122.java)
- [**lengthOfLIS-1**](data_struct_study/src/dynamic_problem/Solution300.java)
- [**lengthOfLIS-2**](data_struct_study/src/dynamic_problem/Solution300_2.java)
- [**longestCommonSubsequence-1**](data_struct_study/src/dynamic_problem/Solution1143.java)
- [**longestCommonSubsequence-2**](data_struct_study/src/dynamic_problem/Solution1143_2.java)
- [maxSubArray](data_struct_study/src/dynamic_problem/Solution53.java)
- [uniquePaths](data_struct_study/src/dynamic_problem/Solution62.java)
- [minPathSum](data_struct_study/src/dynamic_problem/Solution64.java)
- [minDistance](data_struct_study/src/dynamic_problem/Solution72.java)
- [numDecodings](data_struct_study/src/dynamic_problem/Solution91.java)
- [wordBreak](data_struct_study/src/dynamic_problem/Solution139.java)
- [rob-1](data_struct_study/src/dynamic_problem/Solution198.java)
- [rob-2](data_struct_study/src/dynamic_problem/Solution198_2.java)
- [rob-3](data_struct_study/src/dynamic_problem/Solution198_3.java)
- [rob-4](data_struct_study/src/dynamic_problem/Solution198_4.java)
- [rob-5](data_struct_study/src/dynamic_problem/Solution198_5.java)
- [rob-6](data_struct_study/src/dynamic_problem/Solution198_6.java)
- [rob-7](data_struct_study/src/dynamic_problem/Solution198_7.java)
- [rob+](data_struct_study/src/dynamic_problem/Solution213.java)
- [maximalSquare](data_struct_study/src/dynamic_problem/Solution221.java)
- [maxInWindows](data_struct_study/src/dynamic_problem/Solution239.java)
- [numSquare](data_struct_study/src/dynamic_problem/Solution279.java)
- [maxProfit](data_struct_study/src/dynamic_problem/Solution309.java)
- [coinChange](data_struct_study/src/dynamic_problem/Solution322.java)
- [rob](data_struct_study/src/dynamic_problem/Solution337.java)
- [integerBreak-1](data_struct_study/src/dynamic_problem/Solution343.java)
- [integerBreak-2](data_struct_study/src/dynamic_problem/Solution343_2.java)
- [integerBreak-3](data_struct_study/src/dynamic_problem/Solution343_3.java)
- [wiggleMaxLength](data_struct_study/src/dynamic_problem/Solution376.java)
- [canPartition-1](data_struct_study/src/dynamic_problem/Solution416.java)
- [canPartition-2](data_struct_study/src/dynamic_problem/Solution416_2.java)
- [findTargetSumWays-1](data_struct_study/src/dynamic_problem/Solution494.java)
- [findTargetSumWays-2](data_struct_study/src/dynamic_problem/Solution494_2.java)
- [fib-1](data_struct_study/src/dynamic_problem/Solution509.java)
- [fib-2](data_struct_study/src/dynamic_problem/Solution509_2.java)
- [fib-3](data_struct_study/src/dynamic_problem/Solution509_3.java)
## 十二、贪心算法
贪心算法: 它也存在最小生成树与最短路径中。
### Hot Question
- [isSubsequence](data_struct_study/src/dynamic_problem/Solution392.java)
- [eraseOverlapIntervals-1](data_struct_study/src/dynamic_problem/Solution435.java)
- [eraseOverlapIntervals-2](data_struct_study/src/dynamic_problem/Solution435_2.java)
- [findContentChildren-1](data_struct_study/src/dynamic_problem/Solution455.java)
- [findContentChildren-2](data_struct_study/src/dynamic_problem/Solution455_2.java)
## 十三、其它问题
Bloom Filter 布隆过滤器:
- 1、一个很长的二进制向量和一个映射函数。
- 2、用于检索一个元素是否在一个集合中。
- 3、优点是空间和查询时间效率越超一般算法,缺点是有一定的误识别率(仅当存在时)和删除困难,所以仅仅是一个预先处理模块。
位运算操作:
- 1、X & 1 == 1 OR == 0 判断奇偶(X % 2 == 1)
- 2、X = X & (X-1) => 清零最低位的1
- 3、X & -X => 得到最低位的1。
0s 表示一串 0,1s 表示一串 1。
```
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
```
利用 x ^ 1s = \~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
```
1^1^2 = 2
```
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
```
01011011 &
00111100
--------
00011000
```
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
```
01011011 |
00111100
--------
01111111
```
**位与运算技巧**
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
```
01011011 &
01011010
--------
01011010
```
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=\~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
```
10110100 &
01001100
--------
00000100
```
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
**移位运算**
\>\> n 为算术右移,相当于除以 2n,例如 -7 \>\> 2 = -2。
```
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
```
\>\>\> n 为无符号右移,左边会补上 0。例如 -7 \>\>\> 2 = 1073741822。
```
11111111111111111111111111111001 >>> 2
--------
00111111111111111111111111111111
```
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
```
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
```
**mask 计算**
- 要获取 111111111,将 0 取反即可,\~0。
- 要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
- 要得到 1 到 i 位为 1 的 mask,(1<

### 出身普通的人,如何真正改变命运?
这是我过去七年一直研究的命题。首先,是为自己研究,因为我是从小城镇出来的,通过持续不断地逆袭立足深圳。**越是出身普通的人,就越需要有耐心,去进行系统性地全面提升,这方面,我有非常丰富的实践经验和方法论**。因此,我开启了 “JsonChao” 的成长社群,希望和你一起完成系统性地蜕变。
### 星球目前有哪些服务?
- 每周会提供一份让 **个人增值,避免踩坑 的硬干货**。
- 每日以文字或语音的形式分享我个人学习和实践中的 **思考精华或复盘记录**。
- 提供 **每月 三 次成长**、技术或面试指导的咨询服务。
- 更多服务正在研发中...
### 超哥的知识星球适合谁?
- **如果你希望持续提升自己,获得更高的薪资或是想加入大厂**,那么超哥的知识星球会对你有很大的帮助。
- **如果你既努力,又焦虑**,特别适合加入超哥的知识星球,因为我经历过同样的阶段,而且最后找到了走出焦虑,靠近梦想的地方。
- **如果你希望改变自己的生活状态**,欢迎加入超哥的知识星球,和我一起每日迭代,持续精进。

## 公众号
我的公众号 `JsonChao` 开通啦,专注于构建一套未来Android开发必备的知识体系。每个工作日为您推送高质量文章,让你每天都能涨知识。如果您想第一时间获取最新文章和最新动态,欢迎扫描关注~
