Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/adonath/gmmx
Gaussian Mixture Models in Jax
https://github.com/adonath/gmmx
Last synced: 12 days ago
JSON representation
Gaussian Mixture Models in Jax
- Host: GitHub
- URL: https://github.com/adonath/gmmx
- Owner: adonath
- License: bsd-3-clause
- Created: 2024-10-28T14:53:20.000Z (2 months ago)
- Default Branch: main
- Last Pushed: 2024-12-18T20:36:15.000Z (16 days ago)
- Last Synced: 2024-12-18T21:30:52.850Z (16 days ago)
- Language: Python
- Homepage:
- Size: 1.25 MB
- Stars: 1
- Watchers: 1
- Forks: 0
- Open Issues: 1
-
Metadata Files:
- Readme: README.md
- Contributing: CONTRIBUTING.md
- License: LICENSE
- Citation: CITATION.cff
Awesome Lists containing this project
README
# GMMX: Gaussian Mixture Models in Jax
[](https://img.shields.io/github/v/release/adonath/gmmx)
[](https://github.com/adonath/gmmx/actions/workflows/main.yml?query=branch%3Amain)
[](https://codecov.io/gh/adonath/gmmx)
[](https://img.shields.io/github/commit-activity/m/adonath/gmmx)
[](https://img.shields.io/github/license/adonath/gmmx)
[](https://doi.org/10.5281/zenodo.14515326)
A minimal implementation of Gaussian Mixture Models in Jax
- **Github repository**:
- **Documentation**
## Installation
`gmmx` can be installed via pip:
```bash
pip install gmmx
```
## Usage
```python
from gmmx import GaussianMixtureModelJax, EMFitter
# Create a Gaussian Mixture Model with 16 components and 32 features
gmm = GaussianMixtureModelJax.create(n_components=16, n_features=32)
# Draw samples from the model
n_samples = 10_000
x = gmm.sample(n_samples)
# Fit the model to the data
em_fitter = EMFitter(tol=1e-3, max_iter=100)
gmm_fitted = em_fitter.fit(x=x, gmm=gmm)
```
If you use the code in a scientific publication, please cite the Zenodo DOI from the badge above.
## Why Gaussian Mixture models?
What are Gaussian Mixture Models (GMM) useful for in the age of deep learning? GMMs might have come out of fashion for classification tasks, but they still
have a few properties that make them useful in certain scenarios:
- They are universal approximators, meaning that given enough components they can approximate any distribution.
- Their likelihood can be evaluated in closed form, which makes them useful for generative modeling.
- They are rather fast to train and evaluate.
I would strongly recommend to read [In Depth: Gaussian Mixture Models](https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html) from the Python Data Science Handbook for a more in-depth introduction to GMMs and their
application as density estimators.
One of these applications in my research is the context of image reconstruction, where GMMs can be used to model the distribution and pixel correlations of local (patch based)
image features. This can be useful for tasks like image denoising or inpainting. One of these methods I have used them for is [Jolideco](https://github.com/jolideco/jolideco).
Speed up the training of O(10^6) patches was the main motivation for `gmmx`.
## Benchmarks
Here are some results from the benchmarks in the [examples/benchmarks](https://github.com/adonath/gmmx/tree/main/examples/benchmarks) folder comparing against Scikit-Learn. The benchmarks were run on an "Intel(R) Xeon(R) Gold 6338" CPU and a single "NVIDIA L40S" GPU.
### Prediction Time
| Time vs. Number of Components | Time vs. Number of Samples | Time vs. Number of Features |
| ----------------------------------------------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------- |
|  |  |  |
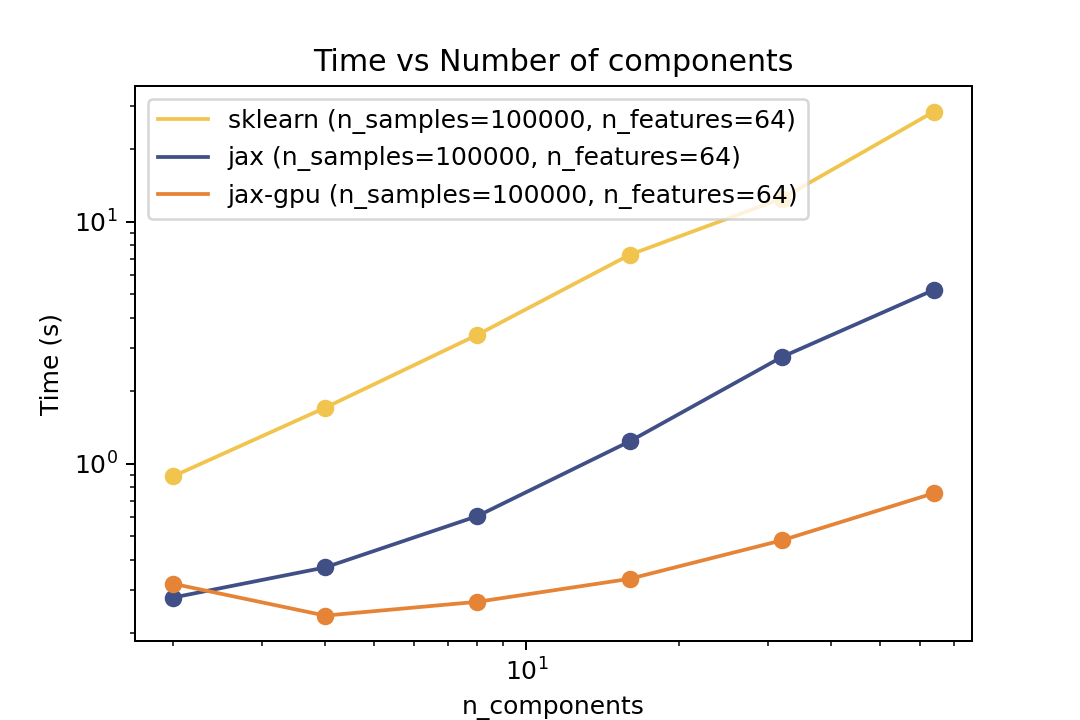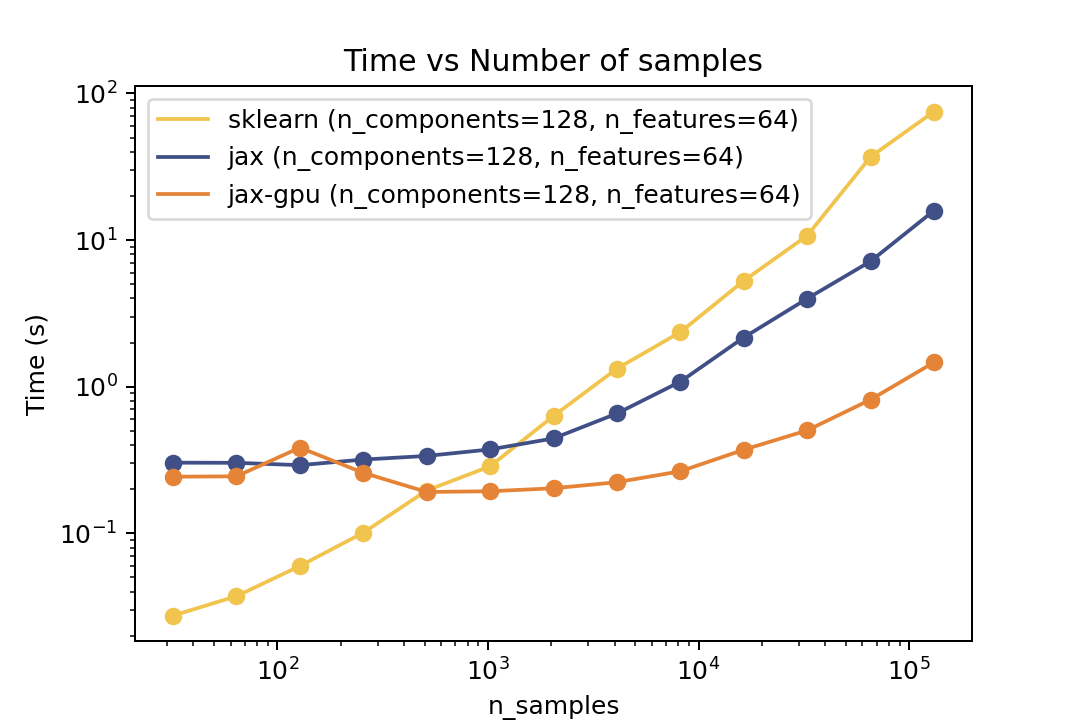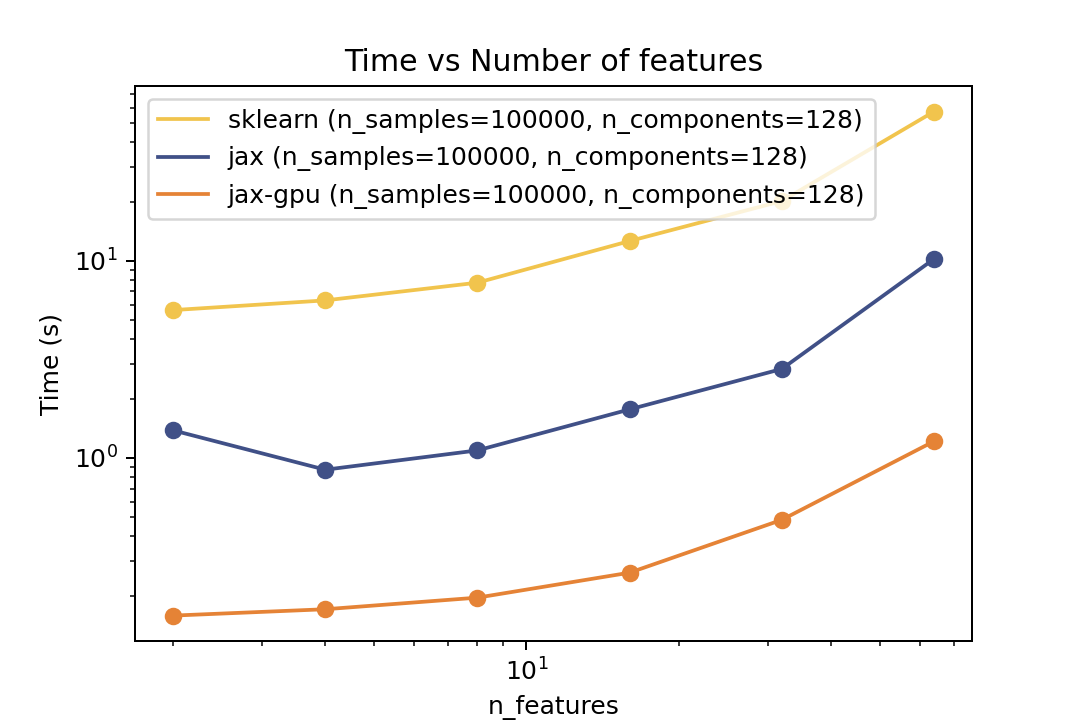For prediction the speedup is around 5-6x for varying number of components and features and ~50x speedup on the GPU. For the number of samples the cross-over point is around O(10^3) samples.
### Training Time
| Time vs. Number of Components | Time vs. Number of Samples | Time vs. Number of Features |
| ------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------------------------------------- |
|  |  |  |
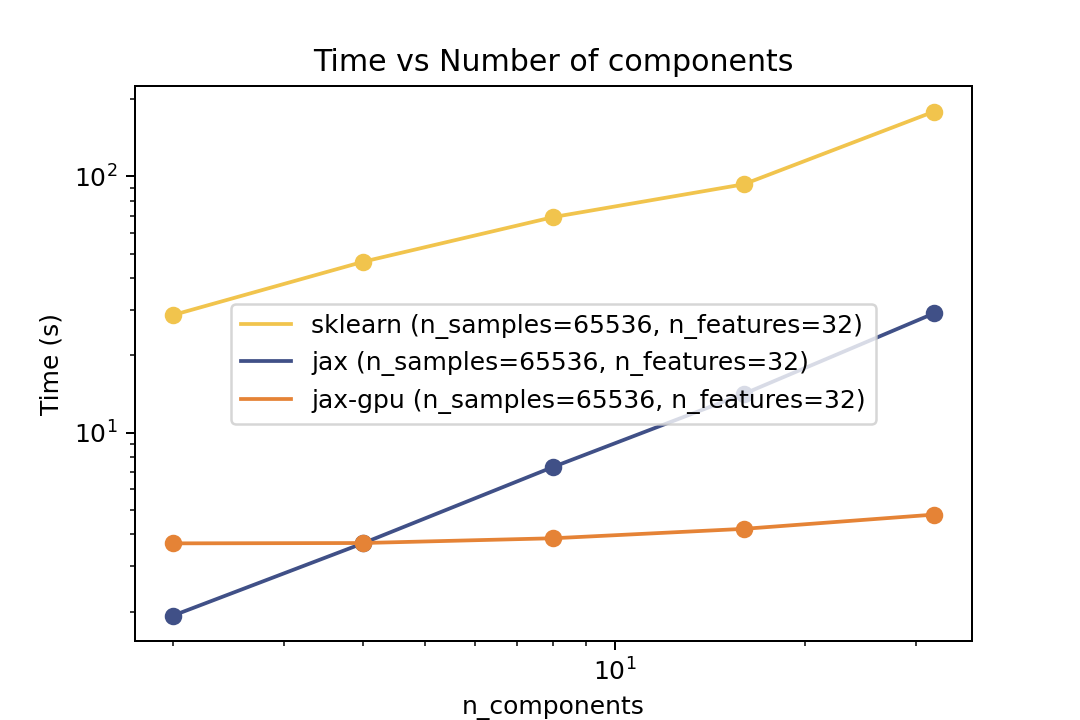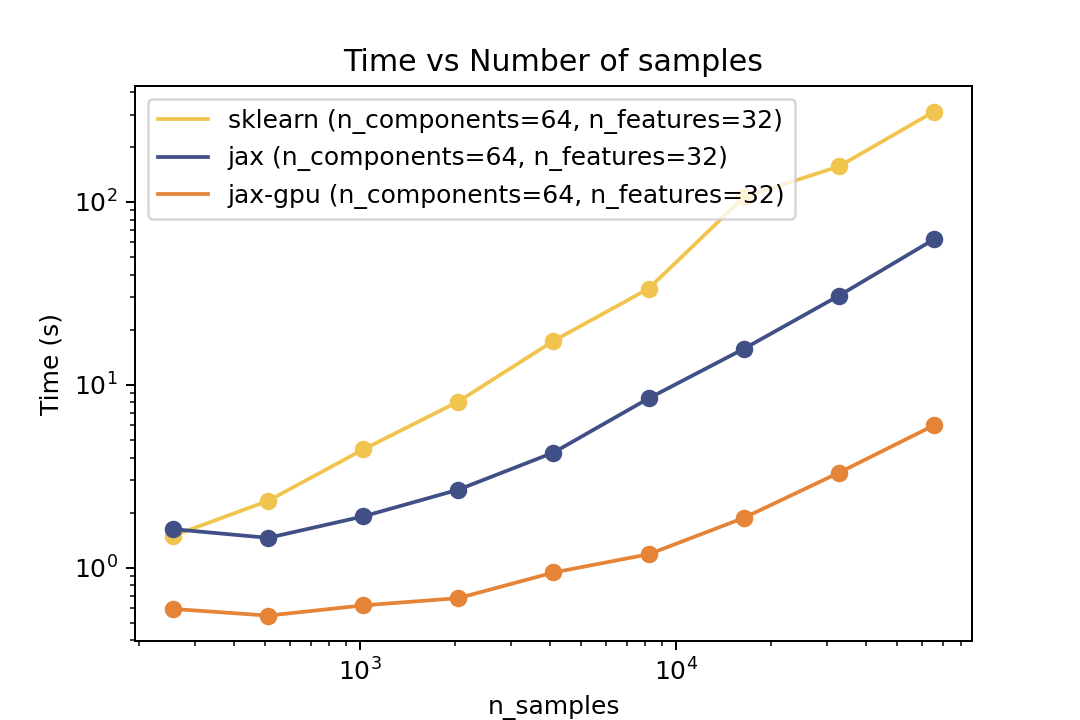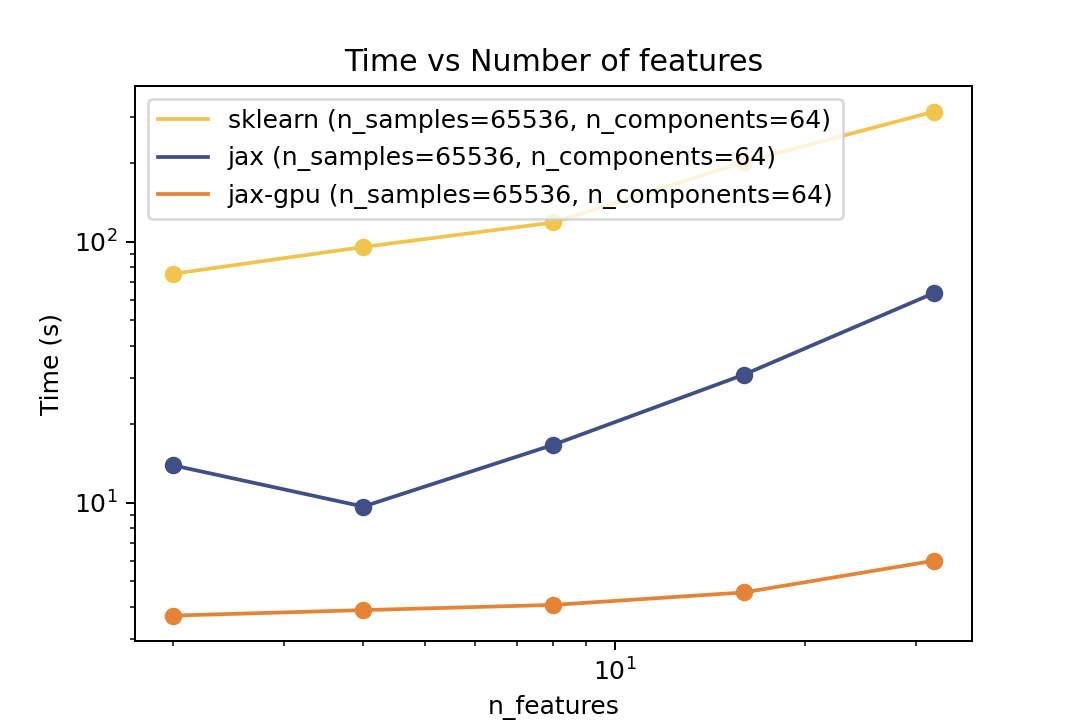For training the speedup is around ~5-6x on the same architecture and ~50x speedup on the GPU. In the bechmark I have forced both fitters to evaluate exactly the same number of iterations. However in general there is no guarantee that GMMX converges to the same solution as Scikit-Learn. But there are some tests in the `tests` folder that compare the results of the two implementations which shows good agreement.