https://github.com/alejo1630/4bar_mechanism

This Python Notebook is a tool to calculate the kinematic model (position, velocity and acceleration) for a 4-bar mechanism in several configurations
https://github.com/alejo1630/4bar_mechanism

4barmechanism jupyter-notebook kinematic-modeling python

Last synced: 8 days ago
JSON representation

This Python Notebook is a tool to calculate the kinematic model (position, velocity and acceleration) for a 4-bar mechanism in several configurations

• Host: GitHub
• URL: https://github.com/alejo1630/4bar_mechanism
• Owner: alejo1630
• Created: 2023-07-02T22:29:58.000Z (over 1 year ago)
• Default Branch: main
• Last Pushed: 2023-10-01T18:50:40.000Z (about 1 year ago)
• Last Synced: 2023-10-01T22:32:33.751Z (about 1 year ago)
• Topics: 4barmechanism, jupyter-notebook, kinematic-modeling, python
• Language: Jupyter Notebook
• Homepage:
• Size: 7.67 MB
• Stars: 1
• Watchers: 1
• Forks: 0
• Open Issues: 0
• Metadata Files:
  • Readme: README.md

Awesome Lists containing this project

README

        
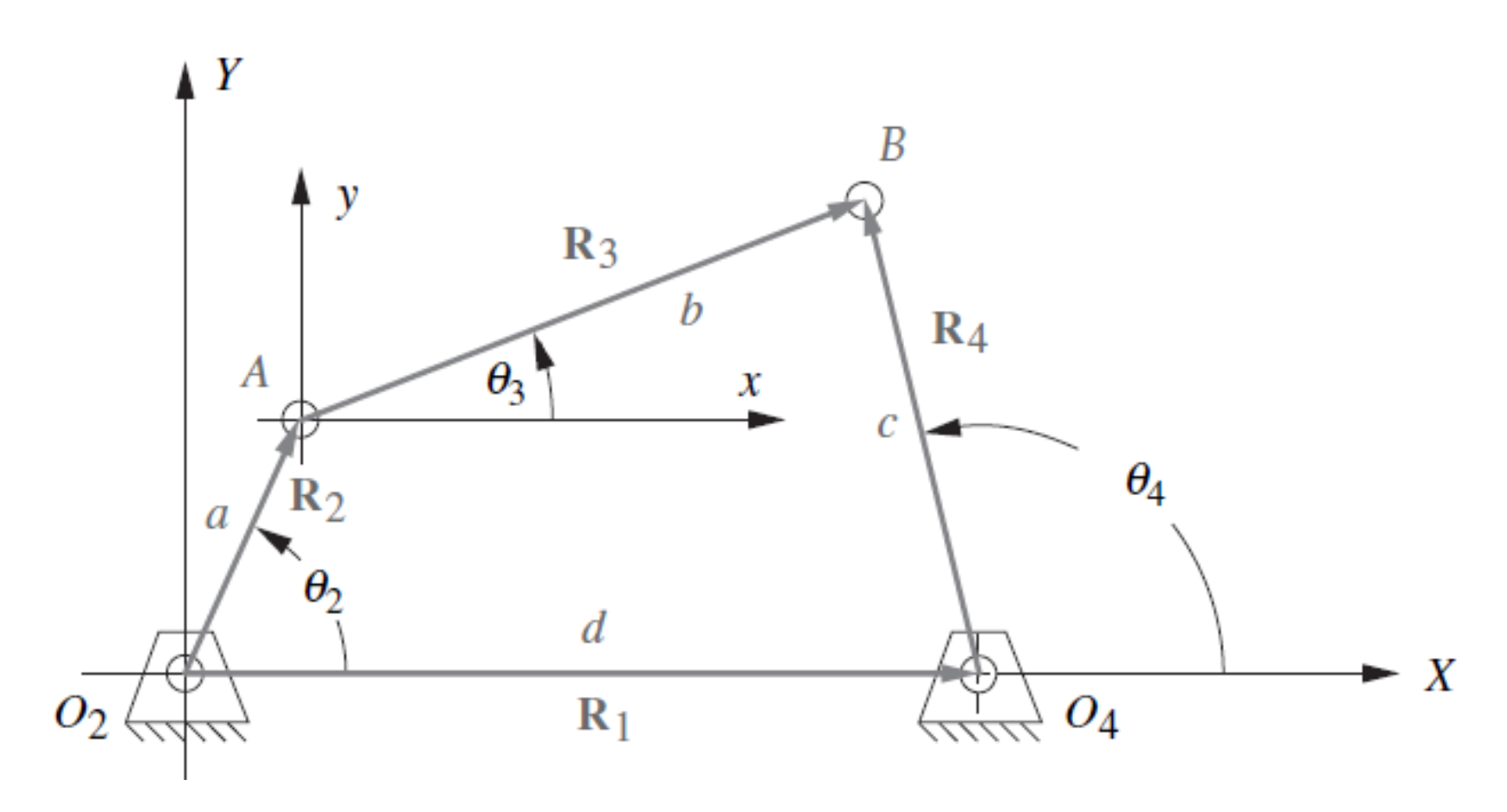
# 4 bar Mechanism

This Python Notebook is a tool to calculate the kinematic model (position, velocity and acceleration) for a 4-bar mechanism in several configurations



## 🔰 How does it work?

* User has to input the size of the 4 linkage bars $(a, b, c, d)$

* Linkage bars are classified based on their sizes

  * $S:$ Shortest member

  * $L:$ Longest member

  * $P, Q:$ Remaining members

* Grashof condition is applied in order to classify the 4-bar mechanism

### Grashof Mechanism

$$S + L < P + Q$$

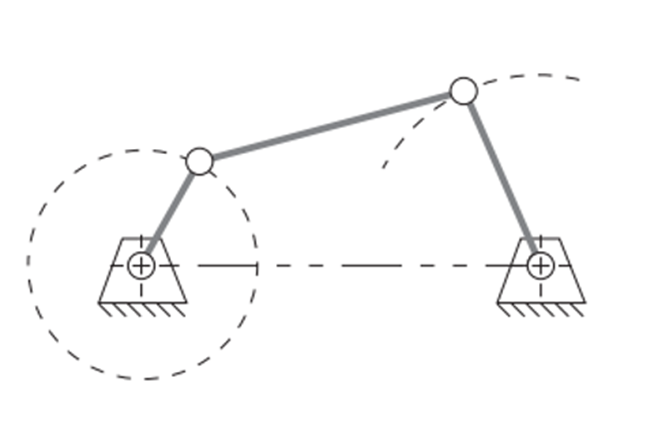
* **Crank and Rocker Mechanism**: Occurs when the ground link $d$ is the shortest member $(S)$



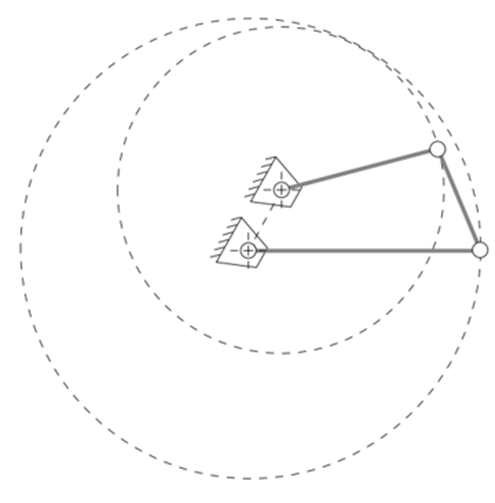
* **Double Crank Mechanism**: Occurs when linkage bars $a$ or $c$ are the shortest member $(S)$



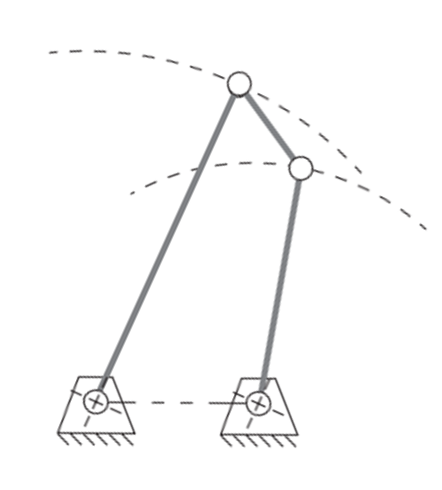
* **Double Rocker Mechanism**: Occurs when the couples link $b$ is the shortest member $(S)$



### Triple Rocker Mechanism

$$S + L > P + Q$$



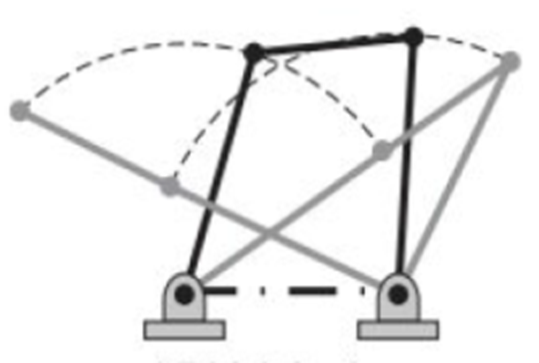
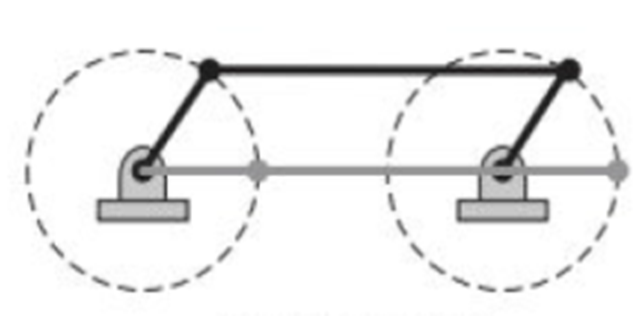
### Change Point State

$$S + L = P + Q$$



* User hast to enter the initial angular position, angular velocity and angular acceleration. In addtion, time and time-step have to be defined.

* The kinematics models is derived using the vectorial representation of the 4 bar mechanism, getting the **Freudenstein's Equations**

### Position Analysis

Position analysis is performed solving the following equations. One of the three angles had to have been defined by the user, so it would be a system of two equations and two unknowns. 

**Real Part**

$$a\cos{\theta_2} + b\cos{\theta_3} - c\cos{\theta_4} - d = 0$$

**Imaginary Part**

$$a\sin{\theta_2} + b\sin{\theta_3} - c\sin{\theta_4} = 0$$

Due to the angles are related with trigonometric functions, Newton-Raphson method is used for solving the equations.



### Velocity Analysis



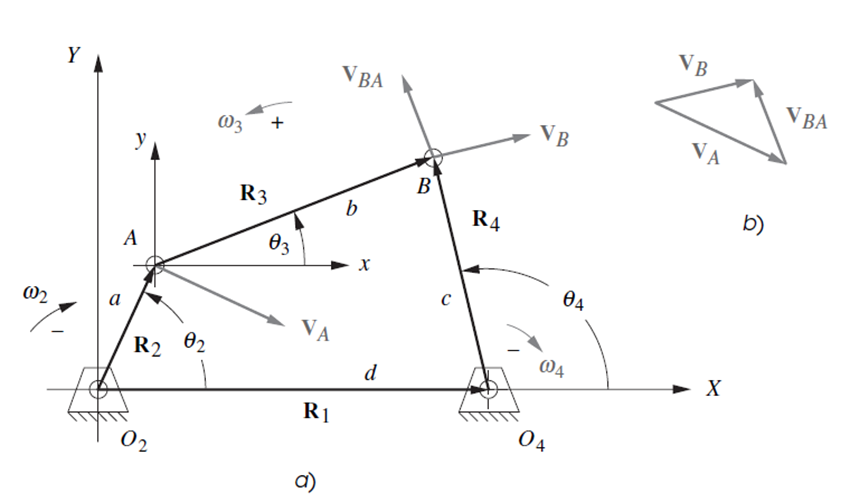
The velocity analysis is performed based on the following systems of linear equations

**Real Part**

$$-a\omega_2\sin{\theta_2} - b\omega_3\sin{\theta_3} + c\omega_4\sin{\theta_4} = 0$$

**Imaginary Part**

$$a\omega_2\cos{\theta_2} + b\omega_3\cos{\theta_3} - c\omega_4\cos{\theta_4} = 0$$

## Acceleration Analysis



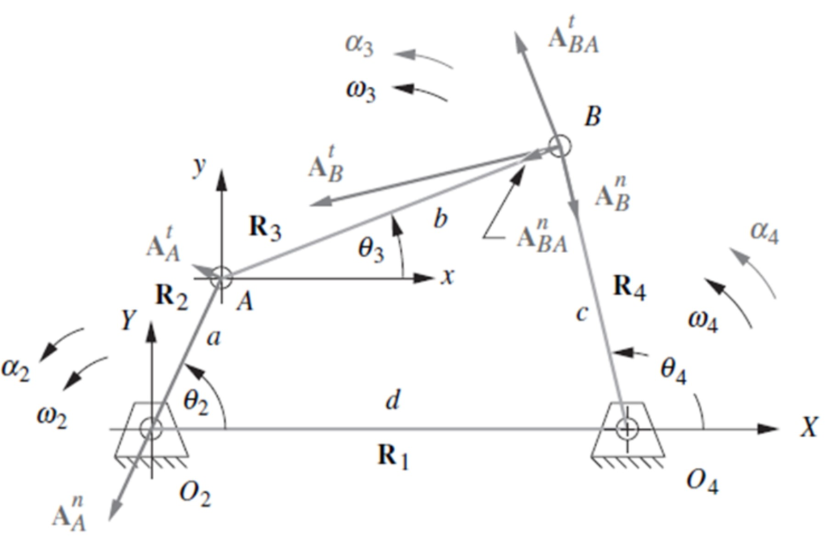
The acceleration analysis is performed based on the following systems of linear equations

**Real Part**

$$-a\alpha_2\sin{\theta_2}-a\omega_2^2\cos{\theta_2}-b\alpha_3\sin{\theta_3}-b\omega_3^2\cos{\theta_3}+c\alpha_4\sin{\theta_4}+c\omega_4^2\cos{\theta_4} = 0$$

**Imaginary Part**

$$a\alpha_2\cos{\theta_2}-a\omega_2^2\sin{\theta_2}+b\alpha_3\cos{\theta_3}-b\omega_3^2\sin{\theta_3}-c\alpha_4\cos{\theta_4}+c\omega_4^2\sin{\theta_4} = 0$$