https://github.com/andrew-johnson-4/ai4p
An inference that always brings peace
https://github.com/andrew-johnson-4/ai4p
Last synced: 8 months ago
JSON representation
An inference that always brings peace
- Host: GitHub
- URL: https://github.com/andrew-johnson-4/ai4p
- Owner: andrew-johnson-4
- License: mit
- Created: 2024-07-28T06:45:00.000Z (about 1 year ago)
- Default Branch: main
- Last Pushed: 2025-02-07T06:10:59.000Z (8 months ago)
- Last Synced: 2025-02-22T03:47:24.409Z (8 months ago)
- Size: 52.7 KB
- Stars: 2
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# AI4P
An inference that always brings peace
### Problem Statement
There are features in programming languages that are desirable by themselves but also run at odds to one another. I have 6 such features and a language that contains all of them but the type inference algorithm is not obvious.
I suspect that strong normalization is possible in this language, but it remains an open problem. When type inference is complete we can say that the program is "at peace" so that is where this project name comes from.
### Language Specification
[Term]
A Term can always be represented as a lambda calculus term.
[Type]
A Type can always be represented nominally with possible internal structure expressable as a lambda calculus term.
Types can be viewed as ordinals or literal strings etc, so these Types are equivalent to types in Simply Typed Lambda Calculus.
[Split]
A Split is a symbolic link to multiple ambiguous Terms.
Any Term position that accepts a Term must accept a Split.
[Join]
A Join is a symbolic link to multiple ambiguous Types.
Any Type position that accepts a Type must accept a Join.
[Projection]
A Projection is a lambda calculus term that can be applied to a Type structure to return another Type.
A Projection must be strongly normalizing.
[Relation]
A relation is a property of comparison of some Terms and Types.
A relation is considered a Boolean Term even though it may reference both Terms AND Types.
Any Term position that accepts a Boolean Term must accept a Relation.
### Constraints
There are some constraints on what constitutes a well-formed language program:
* Each individual Term in a Split is explicitly ascripted with a Type.
* Join Reduction (is only meant to add ad-hoc polymorphism, but there may be other reductions)
There may be additional constraints added to reach strong normalization, but for now I am just considering the shape of the most general problem.
### Example
There have been several attempts so far to implement languages with the above feature set.
Type inference in these languages does seem to be strongly normalizing, but in practice the inference is often intractable.
The following algorithm has been discovered as effective to bring this inference in line with expectations for runtime efficiency.
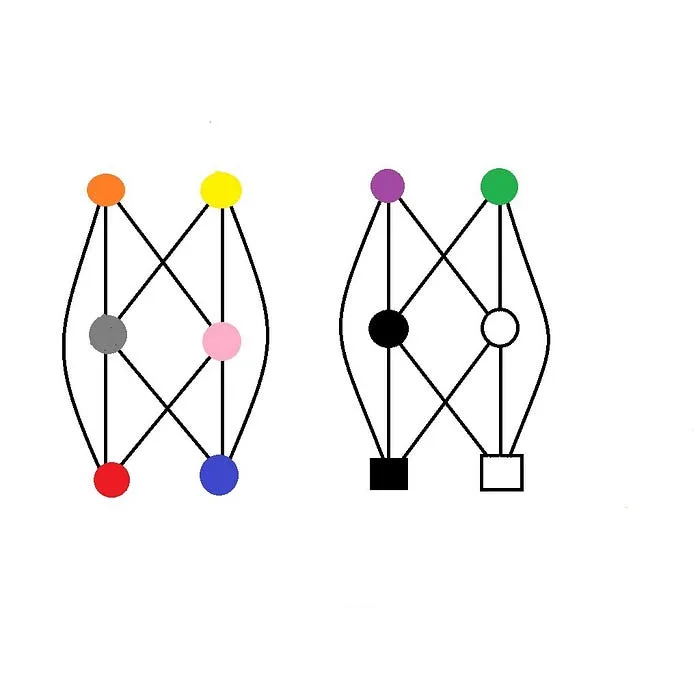
To read this diagram, the left and the right are both state machines, having a "position" at one of the nodes at any given time.
To use this during inference the following information is tracked:
* Current location (t) + embedding
* Previous location (t-1) + embedding
Then the inference tries to predict the best embedding to move towards.
An embedding is a single step of natural induction.
Each color is assigned by the inference algorithm and can be used to explore a high-dimensional space.
Depending on the algorithm used, inference may fail, and back-tracking can be used to reground the state.
Here is an embedding from one particular inference algorithm.
| name | descriptive name | definition
|------------|------------------------------|--------------------------
| black circle | term | a
| black line | term | a(b)
| white circle | type | B
| white line | type | A->B
| yellow circle | join | let a: A; let b: A
| yellow line | join | let f: A->C; let f: B->C
| orange circle | split | let a: A; let a: B
| orange line | split | let f: A->B; let f: A->C
| red circle | less | ≤
| red line | less | ≤
| blue circle | more | ≥
| blue line | more | ≥
| purple circle | up | +
| purple line | up | +
| green circle | down | -
| green line | down | -
| pink circle | parallel | \|\|
| pink line | parallel | \|\|
| grey circle | perpendicular | ⊥
| grey line | perpendicular | ⊥
This embedding only uses 10 colors. So the state machine is customizable, although there tends to be overlap.