Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/andyobtiva/perfect-shape

Perfect Shape is a collection of geometric algorithms that are mostly useful for GUI manipulation like checking containment of a point in popular geometric shapes such as rectangle, square, arc, circle, polygon, and paths containing lines, quadratic bézier curves, and cubic bezier curves. Also, some general math algorithms like IEEE-754 Remainder.
https://github.com/andyobtiva/perfect-shape

algorithm algorithms even-odd-rule geometry nonzero-rule ray-casting-algorithm raycasting-algorithm ruby ruby-gem rubygem winding-number-algorithm

Last synced: 19 days ago
JSON representation

Perfect Shape is a collection of geometric algorithms that are mostly useful for GUI manipulation like checking containment of a point in popular geometric shapes such as rectangle, square, arc, circle, polygon, and paths containing lines, quadratic bézier curves, and cubic bezier curves. Also, some general math algorithms like IEEE-754 Remainder.

Awesome Lists containing this project

README 

        
# Perfect Shape 1.0.8

## Geometric Algorithms

[![Gem Version](https://badge.fury.io/rb/perfect-shape.svg)](http://badge.fury.io/rb/perfect-shape)

[![Test](https://github.com/AndyObtiva/perfect-shape/actions/workflows/ruby.yml/badge.svg)](https://github.com/AndyObtiva/perfect-shape/actions/workflows/ruby.yml)



([Used by Fukuoka 2022 Special Award Winning Glimmer DSL for LibUI Ruby Desktop Development GUI Library](https://github.com/AndyObtiva/glimmer-dsl-libui))



[`PerfectShape`](https://rubygems.org/gems/perfect-shape) is a collection of pure Ruby geometric algorithms that are mostly useful for GUI (Graphical User Interface) manipulation like checking viewport rectangle intersection or containment of a mouse click [point](#perfectshapepoint) in popular geometry shapes such as [rectangle](#perfectshaperectangle), [square](#perfectshapesquare), [arc](#perfectshapearc) (open, chord, and pie), [ellipse](#perfectshapeellipse), [circle](#perfectshapecircle), [polygon](#perfectshapepolygon), and [paths](#perfectshapepath) containing [lines](#perfectshapeline), [quadratic bézier curves](#perfectshapequadraticbeziercurve), and [cubic bezier curves](#perfectshapecubicbeziercurve), potentially with [affine transforms](#perfectshapeaffinetransform) applied like translation, scale, rotation, shear/skew, and inversion (including both the [Ray Casting Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon#Ray_casting_algorithm), aka [Even-odd Rule](https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule), and the [Winding Number Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon#Winding_number_algorithm), aka [Nonzero Rule](https://en.wikipedia.org/wiki/Nonzero-rule)).



Additionally, [`PerfectShape::Math`](#perfectshapemath) contains some purely mathematical algorithms, like [IEEE 754-1985 Remainder](https://en.wikipedia.org/wiki/IEEE_754-1985).



To ensure accuracy and precision, this library does all its mathematical operations with [`BigDecimal`](https://ruby-doc.org/stdlib-3.0.2/libdoc/bigdecimal/rdoc/BigDecimal.html) numbers.



## Setup



Run:



```

gem install perfect-shape -v 1.0.8

```



Or include in Bundler `Gemfile`:



```ruby

gem 'perfect-shape', '~> 1.0.8'

```



And, run:



```

bundle

```



## API



### `PerfectShape::Math`



Module



- `::degrees_to_radians(angle)`: converts degrees to radians

- `::radians_to_degrees(angle)`: converts radians to degrees

- `::normalize_degrees(angle)`: normalizes the specified angle into the range -180 to 180.

- `::ieee_remainder(x, y)` (alias: `ieee754_remainder`): [IEEE 754-1985 Remainder](https://en.wikipedia.org/wiki/IEEE_754-1985) (different from standard `%` modulo operator as it operates on floats and could return a negative result)



### `PerfectShape::Shape`



Class



This is a base class for all shapes. It is not meant to be used directly. Subclasses implement/override its methods as needed.



- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width

- `#height`: height

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height just as those of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside if `outline` is `false` or if point is on the outline if `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a shape from its outline more successfully



### `PerfectShape::PointLocation`



Module



- `#initialize(x: 0, y: 0)`: initializes a point location, usually representing the top-left point in a shape

- `#x`: top-left x

- `#y`: top-left y

- `#min_x`: min x (x by default)

- `#min_y`: min y (y by default)

- `#first_point`: first point for shape including this module (always assumes top-left corner)



### `PerfectShape::RectangularShape`



Module



Includes `PerfectShape::PointLocation`



- `#initialize(x: 0, y: 0, width: 1, height: 1)`: initializes a rectangular shape

- `#x`: top-left x

- `#y`: top-left y

- `#width`: width

- `#height`: height

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y



### `PerfectShape::MultiPoint`



Module



- `::normalize_point_array`: normalizes `Array` of multiple points into (x,y) point coordinate `Array` format per point

- `#initialize(points: [])`: initializes `points` with `Array` of multiple points (e.g. useful for shapes like `Line` and `Polygon`).

- `#points`: `Array` of multiple points

- `#min_x`: min x of all points

- `#min_y`: min y of all points

- `#max_x`: max x of all points

- `#max_y`: max y of all points

- `#first_point`: first point for shape including this module



### `PerfectShape::AffineTransform`



Class



Affine transforms have the following matrix:



[ xxp xyp xt ]


[ yxp yyp yt ]



The matrix is used to transform (x,y) point coordinates as follows:



[ xxp xyp xt ] * [x] = [ xxp * x + xyp * y + xt ]


[ yxp yyp yt ] * [y] = [ yxp * x + yyp * y + yt ]



`xxp` is the x coordinate x product (`m11`)


`xyp` is the x coordinate y product (`m12`)


`yxp` is the y coordinate x product (`m21`)


`yyp` is the y coordinate y product (`m22`)


`xt` is the x coordinate translation (`m13`)


`yt` is the y coordinate translation (`m23`)



Affine transform mutation operations ending with `!` can be chained as they all return `self`.



- `::new(xxp_element = nil, xyp_element = nil, yxp_element = nil, yyp_element = nil, xt_element = nil, yt_element = nil,

         xxp: nil, xyp: nil, yxp: nil, yyp: nil, xt: nil, yt: nil,

         m11: nil, m12: nil, m21: nil, m22: nil, m13: nil, m23: nil)`:

  The constructor accepts either the (x,y)-operation related argument/kwarg names or traditional matrix element kwarg names. If no arguments are supplied, it constructs an identity matrix (i.e. like calling `::new(xxp: 1, xyp: 0, yxp: 0, yyp: 1, xt: 0, yt: 0)`).

- `#matrix_3d`: Returns Ruby `Matrix` object representing affine transform in 3D (used internally for performing multiplication)

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#identity!` (alias: `reset!`): Resets to identity matrix (i.e. like calling `::new(xxp: 1, xyp: 0, yxp: 0, yyp: 1, xt: 0, yt: 0)`)

- `#invertible?` Returns `true` if matrix is invertible and `false` otherwise

- `#invert!`: Inverts affine transform matrix if invertible or raises an error otherwise

- `#multiply!(other)`: Multiplies affine transform with another affine transform, storing resulting changes in matrix elements

- `#translate!(x_or_point, y=nil)`: Translates affine transform with (x, y) translation values

- `#scale!(x_or_point, y=nil)`: Scales affine transform with (x, y) scale values

- `#rotate!(degrees)`: Rotates by angle degrees counter-clockwise if angle value is positive or clockwise if angle value is negative. Note that it returns very close approximate results for rotations that are 90/180/270 degrees (good enough for inverse-transform GUI point containment checks needed when checking if mouse-click-point is inside a transformed shape).

- `#shear!(x_or_point, y=nil)`: Shears by x and y factors

- `#clone`: Returns a new AffineTransform with the same matrix elements

- `#transform_point(x_or_point, y=nil)`: returns `[xxp * x + xyp * y + xt, yxp * x + yyp * y + yt]`. Note that result is a close approximation, but should be good enough for GUI mouse-click-point containment checks.

- `#transform_points(*xy_coordinates_or_points)`: returns `Array` of (x,y) pair `Array`s transformed with `#transform_point` method

- `#inverse_transform_point(x_or_point, y=nil)`: returns inverse transform of a point (x,y) coordinates (clones self and inverts clone, and then transforms point). Note that result is a close approximation, but should be good enough for GUI mouse-click-point containment checks.

- `#inverse_transform_points(*xy_coordinates_or_points)`: returns inverse transforms of a point `Array` of (x,y) coordinates



Example:



```ruby

xxp = 2

xyp = 3

yxp = 4

yyp = 5

xt = 6

yt = 7

affine_transform1 = PerfectShape::AffineTransform.new(xxp: xxp, xyp: xyp, yxp: yxp, yyp: yyp, xt: xt, yt: yt) # (x,y)-operation kwarg names

affine_transform2 = PerfectShape::AffineTransform.new(m11: xxp, m12: xyp, m21: yxp, m22: yyp, m13: xt, m23: yt) # traditional matrix element kwarg names

affine_transform3 = PerfectShape::AffineTransform.new(xxp, xyp, yxp, yyp, xt, yt) # standard arguments



affine_transform2.matrix_3d == affine_transform1.matrix_3d # => true

affine_transform3.matrix_3d == affine_transform1.matrix_3d # => true



affine_transform = PerfectShape::AffineTransform.new.translate!(30, 20).scale!(2, 3)



affine_transform.transform_point(10, 10) # => approximately [50, 50]

affine_transform.inverse_transform_point(50, 50) # => approximately [10, 10]

```



### `PerfectShape::Point`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::PointLocation`



![point](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/point.png)



Points are simply represented by an `Array` of `[x,y]` coordinates when used within other shapes, but when needing point-specific operations like `point_distance`, the `PerfectShape::Point` class can come in handy.



- `::point_distance(x, y, px, py)`: Returns the distance from a point to another point

- `::normalize_point(x_or_point, y = nil)`: Normalizes point args whether two-number `point` `Array` or `x`, `y` args, returning normalized point `Array` of two `BigDecimal`'s

- `::new(x_or_point=nil, y_arg=nil, x: nil, y: nil)`: constructs a point with (x,y) pair (default: 0,0) whether specified as `Array` of (x,y) pair, flat `x,y` args, or `x:, y:` kwargs.

- `#min_x`: min x (always x)

- `#min_y`: min y (always y)

- `#max_x`: max x (always x)

- `#max_y`: max y (always y)

- `#width`: width (always 0)

- `#height`: height (always 0)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x (always x)

- `#center_y`: center y (always y)

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: true, distance_tolerance: 0)`: checks if point matches self, with a distance tolerance (0 by default). Distance tolerance provides a fuzz factor that for example enables GUI users to mouse-click-select a point shape more successfully. `outline` option makes no difference on point

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#point_distance(x_or_point, y=nil)`: Returns the distance from a point to another point



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Point.new(x: 200, y: 150)



shape.contain?(200, 150) # => true

shape.contain?([200, 150]) # => true

shape.contain?(200, 151) # => false

shape.contain?([200, 151]) # => false

shape.contain?(200, 151, distance_tolerance: 5) # => true

shape.contain?([200, 151], distance_tolerance: 5) # => true

```



### `PerfectShape::Line`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::MultiPoint`



![line](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/line.png)



- `::relative_counterclockwise(x1, y1, x2, y2, px, py)`: Returns an indicator of where the specified point (px,py) lies with respect to the line segment from (x1,y1) to (x2,y2). The return value can be either 1, -1, or 0 and indicates in which direction the specified line must pivot around its first end point, (x1,y1), in order to point at the specified point (px,py). A return value of 1 indicates that the line segment must turn in the direction that takes the positive X axis towards the negative Y axis. In the default coordinate system, this direction is counterclockwise. A return value of -1 indicates that the line segment must turn in the direction that takes the positive X axis towards the positive Y axis. In the default coordinate system, this direction is clockwise. A return value of 0 indicates that the point lies exactly on the line segment. Note that an indicator value of 0 is rare and not useful for determining collinearity because of floating point rounding issues. If the point is colinear with the line segment, but not between the end points, then the value will be -1 if the point lies “beyond (x1,y1)” or 1 if the point lies “beyond (x2,y2)”.

- `::point_distance_square(x1, y1, x2, y2, px, py)`: Returns the square of distance from a point to a line segment.

- `::point_distance(x1, y1, x2, y2, px, py)`: Returns the distance from a point to a line segment.

- `::new(points: [])`: constructs a line with two `points` as `Array` of `Array`s of `[x,y]` pairs or flattened `Array` of alternating x and y coordinates

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: true, distance_tolerance: 0)`: checks if point lies on line, with a distance tolerance (0 by default). Distance tolerance provides a fuzz factor that for example enables GUI users to mouse-click-select a line shape more successfully. `outline` option makes no difference on line

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#relative_counterclockwise(x_or_point, y=nil)`: Returns an indicator of where the specified point (px,py) lies with respect to the line segment from (x1,y1) to (x2,y2). The return value can be either 1, -1, or 0 and indicates in which direction the specified line must pivot around its first end point, (x1,y1), in order to point at the specified point (px,py). A return value of 1 indicates that the line segment must turn in the direction that takes the positive X axis towards the negative Y axis. In the default coordinate system, this direction is counterclockwise. A return value of -1 indicates that the line segment must turn in the direction that takes the positive X axis towards the positive Y axis. In the default coordinate system, this direction is clockwise. A return value of 0 indicates that the point lies exactly on the line segment. Note that an indicator value of 0 is rare and not useful for determining collinearity because of floating point rounding issues. If the point is colinear with the line segment, but not between the end points, then the value will be -1 if the point lies “beyond (x1,y1)” or 1 if the point lies “beyond (x2,y2)”.

- `#point_distance(x_or_point, y=nil)`: Returns the distance from a point to a line segment.

- `#rect_crossings(rxmin, rymin, rxmax, rymax, crossings = 0)`: rectangle crossings (adds to crossings arg)



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Line.new(points: [[0, 0], [100, 100]]) # start point and end point



shape.contain?(50, 50) # => true

shape.contain?([50, 50]) # => true

shape.contain?(50, 51) # => false

shape.contain?([50, 51]) # => false

shape.contain?(50, 51, distance_tolerance: 5) # => true

shape.contain?([50, 51], distance_tolerance: 5) # => true

```



### `PerfectShape::QuadraticBezierCurve`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::MultiPoint`



![quadratic_bezier_curve](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/quadratic_bezier_curve.png)



- `::tag(coord, low, high)`: Determine where coord lies with respect to the range from low to high.  It is assumed that low < high.  The return value is one of the 5 values BELOW, LOWEDGE, INSIDE, HIGHEDGE, or ABOVE.

- `::eqn(val, c1, cp, c2)`: Fill an array with the coefficients of the parametric equation in t, ready for solving against val with solve_quadratic. We currently have: val = Py(t) = C1*(1-t)^2 + 2*CP*t*(1-t) + C2*t^2 = C1 - 2*C1*t + C1*t^2 + 2*CP*t - 2*CP*t^2 + C2*t^2 = C1 + (2*CP - 2*C1)*t + (C1 - 2*CP + C2)*t^2; 0 = (C1 - val) + (2*CP - 2*C1)*t + (C1 - 2*CP + C2)*t^2; 0 = C + Bt + At^2; C = C1 - val; B = 2*CP - 2*C1; A = C1 - 2*CP + C2

- `::solve_quadratic(eqn)`: Solves the quadratic whose coefficients are in the eqn array and places the non-complex roots into the res array, returning the number of roots. The quadratic solved is represented by the equation: 
eqn = {C, B, A}; ax^2 + bx + c = 0
 A return value of `-1` is used to distinguish a constant equation, which might be always 0 or never 0, from an equation that has no zeroes.

- `::eval_quadratic(vals, num, include0, include1, inflect, c1, ctrl, c2)`: Evaluate the t values in the first num slots of the vals[] array and place the evaluated values back into the same array.  Only evaluate t values that are within the range <, >, including the 0 and 1 ends of the range iff the include0 or include1 booleans are true.  If an "inflection" equation is handed in, then any points which represent a point of inflection for that quadratic equation are also ignored.

- `::new(points: [])`: constructs a quadratic bézier curve with three `points` (start point, control point, and end point) as `Array` of `Array`s of `[x,y]` pairs or flattened `Array` of alternating x and y coordinates

- `#points`: points (start point, control point, and end point)

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a quadratic bezier curve shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#curve_center_point`: point at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#curve_center_x`: point x coordinate at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#curve_center_y`: point y coordinate at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#subdivisions(level=1)`: subdivides quadratic bezier curve at its center into into 2 quadratic bezier curves by default, or more if `level` of recursion is specified. The resulting number of subdivisions is `2` to the power of `level`.

- `#point_distance(x_or_point, y=nil, minimum_distance_threshold: OUTLINE_MINIMUM_DISTANCE_THRESHOLD)`: calculates distance from point to curve segment. It does so by subdividing curve into smaller curves and checking against the curve center points until the distance is less than `minimum_distance_threshold`, to avoid being an overly costly operation.

- `#rect_crossings(rxmin, rymin, rxmax, rymax, level, crossings = 0)`: rectangle crossings (adds to crossings arg)



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::QuadraticBezierCurve.new(points: [[200, 150], [270, 320], [380, 150]]) # start point, control point, and end point



shape.contain?(270, 220) # => true

shape.contain?([270, 220]) # => true

shape.contain?(270, 220, outline: true) # => false

shape.contain?([270, 220], outline: true) # => false

shape.contain?(280, 235, outline: true) # => true

shape.contain?([280, 235], outline: true) # => true

shape.contain?(281, 235, outline: true) # => false

shape.contain?([281, 235], outline: true) # => false

shape.contain?(281, 235, outline: true, distance_tolerance: 1) # => true

shape.contain?([281, 235], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::CubicBezierCurve`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::MultiPoint`



![cubic_bezier_curve](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/cubic_bezier_curve.png)



- `::new(points: [])`: constructs a cubic bézier curve with four `points` (start point, two control points, and end point) as `Array` of `Array`s of `[x,y]` pairs or flattened `Array` of alternating x and y coordinates

- `#points`: points (start point, two control points, and end point)

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a cubic bezier curve shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#curve_center_point`: point at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#curve_center_x`: point x coordinate at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#curve_center_y`: point y coordinate at the center of the curve outline (not the center of the bounding box area like `center_x` and `center_y`)

- `#subdivisions(level=1)`: subdivides cubic bezier curve at its center into into 2 cubic bezier curves by default, or more if `level` of recursion is specified. The resulting number of subdivisions is `2` to the power of `level`.

- `#point_distance(x_or_point, y=nil, minimum_distance_threshold: OUTLINE_MINIMUM_DISTANCE_THRESHOLD)`: calculates distance from point to curve segment. It does so by subdividing curve into smaller curves and checking against the curve center points until the distance is less than `minimum_distance_threshold`, to avoid being an overly costly operation.

- `#rectangle_crossings(rectangle)`: rectangle crossings (used to determine rectangle interior intersection), optimized to check if line represented by cubic bezier curve crosses the rectangle first, and if not then perform expensive check with `#rect_crossings`

- `#rect_crossings(rxmin, rymin, rxmax, rymax, level, crossings = 0)`: rectangle crossings (adds to crossings arg)



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::CubicBezierCurve.new(points: [[200, 150], [235, 235], [270, 320], [380, 150]]) # start point, two control points, and end point



shape.contain?(270, 220) # => true

shape.contain?([270, 220]) # => true

shape.contain?(270, 220, outline: true) # => false

shape.contain?([270, 220], outline: true) # => false

shape.contain?(261.875, 245.625, outline: true) # => true

shape.contain?([261.875, 245.625], outline: true) # => true

shape.contain?(261.875, 246.625, outline: true) # => false

shape.contain?([261.875, 246.625], outline: true) # => false

shape.contain?(261.875, 246.625, outline: true, distance_tolerance: 1) # => true

shape.contain?([261.875, 246.625], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Rectangle`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::RectangularShape`



![rectangle](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/rectangle.png)



- `::new(x: 0, y: 0, width: 1, height: 1)`: constructs a rectangle

- `#x`: top-left x

- `#y`: top-left y

- `#width`: width

- `#height`: height

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a rectangle shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#edges`: edges of rectangle as `PerfectShape::Line` objects

- `#out_state(x_or_point, y = nil)`: Returns "out state" of specified point (x,y) (whether it lies to the left, right, top, bottom of rectangle). If point is outside rectangle, it returns a bit mask combination of `Rectangle::OUT_LEFT`, `Rectangle::OUT_RIGHT`, `Rectangle::OUT_TOP`, or `Rectangle::OUT_BOTTOM`. Otherwise, it returns `0` if point is inside the rectangle.

- `#empty?`: Returns `true` if width or height are 0 (or negative) and `false` otherwise

- `#to_path_shapes`: Converts `Rectangle` into basic `Path` shapes made up of `Point`s and `Line`s. Used by `Path` when adding a `Rectangle` to `Path` `shapes`



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Rectangle.new(x: 15, y: 30, width: 200, height: 100)



shape.contain?(115, 80) # => true

shape.contain?([115, 80]) # => true

shape.contain?(115, 80, outline: true) # => false

shape.contain?([115, 80], outline: true) # => false

shape.contain?(115, 30, outline: true) # => true

shape.contain?([115, 30], outline: true) # => true

shape.contain?(115, 31, outline: true) # => false

shape.contain?([115, 31], outline: true) # => false

shape.contain?(115, 31, outline: true, distance_tolerance: 1) # => true

shape.contain?([115, 31], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Square`



Class



Extends `PerfectShape::Rectangle`



![square](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/square.png)



- `::new(x: 0, y: 0, length: 1)` (`length` alias: `size`): constructs a square

- `#x`: top-left x

- `#y`: top-left y

- `#length`: length

- `#width`: width (equal to length)

- `#height`: height (equal to length)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a square shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#edges`: edges of square as `PerfectShape::Line` objects

- `#empty?`: Returns `true` if length is 0 (or negative) and `false` otherwise

- `#to_path_shapes`: Converts `Square` into basic `Path` shapes made up of `Point`s and `Line`s. Used by `Path` when adding a `Square` to `Path` `shapes`



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Square.new(x: 15, y: 30, length: 200)



shape.contain?(115, 130) # => true

shape.contain?([115, 130]) # => true

shape.contain?(115, 130, outline: true) # => false

shape.contain?([115, 130], outline: true) # => false

shape.contain?(115, 30, outline: true) # => true

shape.contain?([115, 30], outline: true) # => true

shape.contain?(115, 31, outline: true) # => false

shape.contain?([115, 31], outline: true) # => false

shape.contain?(115, 31, outline: true, distance_tolerance: 1) # => true

shape.contain?([115, 31], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Arc`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::RectangularShape`



Arcs can be of type `:open`, `:chord`, or `:pie`



Open Arc | Chord Arc | Pie Arc

---------|-----------|--------

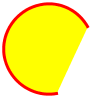![arc-open](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/arc-open.png) | ![arc-chord](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/arc-chord.png) | ![arc-pie](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/arc-pie.png)



- `::new(type: :open, x: 0, y: 0, width: 1, height: 1, start: 0, extent: 360, center_x: nil, center_y: nil, radius_x: nil, radius_y: nil)`: constructs an arc of type  `:open` (default), `:chord`, or `:pie`

- `#type`: `:open`, `:chord`, or `:pie`

- `#x`: top-left x

- `#y`: top-left y

- `#width`: width

- `#height`: height

- `#start`: start angle in degrees

- `#extent`: extent angle in degrees

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#start_point`: start point as `Array` of (x,y) coordinates

- `#end_point`: end point as `Array` of (x,y) coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#radius_x`: radius along the x-axis

- `#radius_y`: radius along the y-axis

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select an arc shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#contain_angle?(angle)`: returns `true` if the angle is within the angular extents of the arc and `false` otherwise

- `#to_path_shapes`: Converts `Arc` into basic `Path` shapes made up of `Point`s, `Line`s, and `CubicBezierCurve`s. Used by `Path` when adding an `Arc` to `Path` `shapes`

- `#btan(increment)`: btan computes the length (k) of the control segments at the beginning and end of a cubic bezier that approximates a segment of an arc with extent less than or equal to 90 degrees.  This length (k) will be used to generate the 2 bezier control points for such a segment.



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Arc.new(type: :open, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)

shape2 = PerfectShape::Arc.new(type: :open, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)



shape.contain?(39.5, 33.0) # => true

shape.contain?([39.5, 33.0]) # => true

shape2.contain?(39.5, 33.0) # => true

shape2.contain?([39.5, 33.0]) # => true

shape.contain?(39.5, 33.0, outline: true) # => false

shape.contain?([39.5, 33.0], outline: true) # => false

shape2.contain?(39.5, 33.0, outline: true) # => false

shape2.contain?([39.5, 33.0], outline: true) # => false

shape.contain?(2.0, 33.0, outline: true) # => true

shape.contain?([2.0, 33.0], outline: true) # => true

shape2.contain?(2.0, 33.0, outline: true) # => true

shape2.contain?([2.0, 33.0], outline: true) # => true

shape.contain?(3.0, 33.0, outline: true) # => false

shape.contain?([3.0, 33.0], outline: true) # => false

shape2.contain?(3.0, 33.0, outline: true) # => false

shape2.contain?([3.0, 33.0], outline: true) # => false

shape.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape2.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape2.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape.contain?(shape.center_x, shape.center_y, outline: true) # => false

shape.contain?([shape.center_x, shape.center_y], outline: true) # => false

shape2.contain?(shape2.center_x, shape2.center_y, outline: true) # => false

shape2.contain?([shape2.center_x, shape2.center_y], outline: true) # => false



shape3 = PerfectShape::Arc.new(type: :chord, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)

shape4 = PerfectShape::Arc.new(type: :chord, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)



shape3.contain?(39.5, 33.0) # => true

shape3.contain?([39.5, 33.0]) # => true

shape4.contain?(39.5, 33.0) # => true

shape4.contain?([39.5, 33.0]) # => true

shape3.contain?(39.5, 33.0, outline: true) # => false

shape3.contain?([39.5, 33.0], outline: true) # => false

shape4.contain?(39.5, 33.0, outline: true) # => false

shape4.contain?([39.5, 33.0], outline: true) # => false

shape3.contain?(2.0, 33.0, outline: true) # => true

shape3.contain?([2.0, 33.0], outline: true) # => true

shape4.contain?(2.0, 33.0, outline: true) # => true

shape4.contain?([2.0, 33.0], outline: true) # => true

shape3.contain?(3.0, 33.0, outline: true) # => false

shape3.contain?([3.0, 33.0], outline: true) # => false

shape4.contain?(3.0, 33.0, outline: true) # => false

shape4.contain?([3.0, 33.0], outline: true) # => false

shape3.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape3.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape4.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape4.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape3.contain?(shape3.center_x, shape3.center_y, outline: true) # => false

shape3.contain?([shape3.center_x, shape3.center_y], outline: true) # => false

shape4.contain?(shape4.center_x, shape4.center_y, outline: true) # => false

shape4.contain?([shape4.center_x, shape4.center_y], outline: true) # => false



shape5 = PerfectShape::Arc.new(type: :pie, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)

shape6 = PerfectShape::Arc.new(type: :pie, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)



shape5.contain?(39.5, 33.0) # => false

shape5.contain?([39.5, 33.0]) # => false

shape6.contain?(39.5, 33.0) # => false

shape6.contain?([39.5, 33.0]) # => false

shape5.contain?(9.5, 33.0) # => true

shape5.contain?([9.5, 33.0]) # => true

shape6.contain?(9.5, 33.0) # => true

shape6.contain?([9.5, 33.0]) # => true

shape5.contain?(39.5, 33.0, outline: true) # => false

shape5.contain?([39.5, 33.0], outline: true) # => false

shape6.contain?(39.5, 33.0, outline: true) # => false

shape6.contain?([39.5, 33.0], outline: true) # => false

shape5.contain?(2.0, 33.0, outline: true) # => true

shape5.contain?([2.0, 33.0], outline: true) # => true

shape6.contain?(2.0, 33.0, outline: true) # => true

shape6.contain?([2.0, 33.0], outline: true) # => true

shape5.contain?(3.0, 33.0, outline: true) # => false

shape5.contain?([3.0, 33.0], outline: true) # => false

shape6.contain?(3.0, 33.0, outline: true) # => false

shape6.contain?([3.0, 33.0], outline: true) # => false

shape5.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape5.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape6.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true

shape6.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true

shape5.contain?(shape5.center_x, shape5.center_y, outline: true) # => true

shape5.contain?([shape5.center_x, shape5.center_y], outline: true) # => true

shape6.contain?(shape6.center_x, shape6.center_y, outline: true) # => true

shape6.contain?([shape6.center_x, shape6.center_y], outline: true) # => true

```



### `PerfectShape::Ellipse`



Class



Extends `PerfectShape::Arc`



![ellipse](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/ellipse.png)



- `::new(x: 0, y: 0, width: 1, height: 1, center_x: nil, center_y: nil, radius_x: nil, radius_y: nil)`: constructs an ellipse

- `#x`: top-left x

- `#y`: top-left y

- `#width`: width

- `#height`: height

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#radius_x`: radius along the x-axis

- `#radius_y`: radius along the y-axis

- `#type`: always `:open`

- `#start`: always `0`

- `#extent`: always `360`

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select an ellipse shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#to_path_shapes`: Converts `Ellipse` into basic `Path` shapes made up of `Point`s, `Line`s, and `CubicBezierCurve`s. Used by `Path` when adding an `Ellipse` to `Path` `shapes`



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Ellipse.new(x: 2, y: 3, width: 50, height: 60)

shape2 = PerfectShape::Ellipse.new(center_x: 27, center_y: 33, radius_x: 25, radius_y: 30)



shape.contain?(27, 33) # => true

shape.contain?([27, 33]) # => true

shape2.contain?(27, 33) # => true

shape2.contain?([27, 33]) # => true

shape.contain?(27, 33, outline: true) # => false

shape.contain?([27, 33], outline: true) # => false

shape2.contain?(27, 33, outline: true) # => false

shape2.contain?([27, 33], outline: true) # => false

shape.contain?(2, 33, outline: true) # => true

shape.contain?([2, 33], outline: true) # => true

shape2.contain?(2, 33, outline: true) # => true

shape2.contain?([2, 33], outline: true) # => true

shape.contain?(1, 33, outline: true) # => false

shape.contain?([1, 33], outline: true) # => false

shape2.contain?(1, 33, outline: true) # => false

shape2.contain?([1, 33], outline: true) # => false

shape.contain?(1, 33, outline: true, distance_tolerance: 1) # => true

shape.contain?([1, 33], outline: true, distance_tolerance: 1) # => true

shape2.contain?(1, 33, outline: true, distance_tolerance: 1) # => true

shape2.contain?([1, 33], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Circle`



Class



Extends `PerfectShape::Ellipse`



![circle](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/circle.png)



- `::new(x: 0, y: 0, diameter: 1, width: 1, height: 1, center_x: nil, center_y: nil, radius: nil, radius_x: nil, radius_y: nil)`: constructs a circle

- `#x`: top-left x

- `#y`: top-left y

- `#diameter`: diameter

- `#width`: width (equal to diameter)

- `#height`: height (equal to diameter)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#radius`: radius

- `#radius_x`: radius along the x-axis (equal to radius)

- `#radius_y`: radius along the y-axis (equal to radius)

- `#type`: always `:open`

- `#start`: always `0`

- `#extent`: always `360`

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: checks if point is inside when `outline` is `false` or if point is on the outline when `outline` is `true`. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a circle shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#to_path_shapes`: Converts `Circle` into basic `Path` shapes made up of `Point`s, `Line`s, and `CubicBezierCurve`s. Used by `Path` when adding a `Circle` to `Path` `shapes`



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Circle.new(x: 2, y: 3, diameter: 60)

shape2 = PerfectShape::Circle.new(center_x: 2 + 30, center_y: 3 + 30, radius: 30)



shape.contain?(32, 33) # => true

shape.contain?([32, 33]) # => true

shape2.contain?(32, 33) # => true

shape2.contain?([32, 33]) # => true

shape.contain?(32, 33, outline: true) # => false

shape.contain?([32, 33], outline: true) # => false

shape2.contain?(32, 33, outline: true) # => false

shape2.contain?([32, 33], outline: true) # => false

shape.contain?(2, 33, outline: true) # => true

shape.contain?([2, 33], outline: true) # => true

shape2.contain?(2, 33, outline: true) # => true

shape2.contain?([2, 33], outline: true) # => true

shape.contain?(1, 33, outline: true) # => false

shape.contain?([1, 33], outline: true) # => false

shape2.contain?(1, 33, outline: true) # => false

shape2.contain?([1, 33], outline: true) # => false

shape.contain?(1, 33, outline: true, distance_tolerance: 1) # => true

shape.contain?([1, 33], outline: true, distance_tolerance: 1) # => true

shape2.contain?(1, 33, outline: true, distance_tolerance: 1) # => true

shape2.contain?([1, 33], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Polygon`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::MultiPoint`



A polygon can be thought of as a special case of [path](#perfectshapepath), consisting of lines only, is closed, and has the [Even-Odd](https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule) winding rule by default.



![polygon](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/polygon.png)



- `::new(points: [], winding_rule: :wind_even_odd)`: constructs a polygon with `points` as `Array` of `Array`s of `[x,y]` pairs or flattened `Array` of alternating x and y coordinates and specified winding rule (`:wind_even_odd` or `:wind_non_zero`)

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: When `outline` is `false`, it checks if point is inside using either the [Ray Casting Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon) (aka [Even-Odd Rule](https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule)) or [Winding Number Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon#Winding_number_algorithm) (aka [Nonzero-Rule](https://en.wikipedia.org/wiki/Nonzero-rule)). Otherwise, when `outline` is `true`, it checks if point is on the outline. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a polygon shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#edges`: edges of polygon as `PerfectShape::Line` objects



Example:



```ruby

require 'perfect-shape'



shape = PerfectShape::Polygon.new(points: [[200, 150], [270, 170], [250, 220], [220, 190], [200, 200], [180, 170]])



shape.contain?(225, 185) # => true

shape.contain?([225, 185]) # => true

shape.contain?(225, 185, outline: true) # => false

shape.contain?([225, 185], outline: true) # => false

shape.contain?(200, 150, outline: true) # => true

shape.contain?([200, 150], outline: true) # => true

shape.contain?(200, 151, outline: true) # => false

shape.contain?([200, 151], outline: true) # => false

shape.contain?(200, 151, outline: true, distance_tolerance: 1) # => true

shape.contain?([200, 151], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::Path`



Class



Extends `PerfectShape::Shape`



Includes `PerfectShape::MultiPoint`



![path](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/path.png)



- `::new(shapes: [], closed: false, winding_rule: :wind_even_odd, line_to_complex_shapes: false)`: constructs a path with `shapes` as `Array` of shape objects, which can be `PerfectShape::Point` (or `Array` of `[x, y]` coordinates), `PerfectShape::Line`, `PerfectShape::QuadraticBezierCurve`, `PerfectShape::CubicBezierCurve`, or complex shapes that decompose into the aforementioned basic path shapes, like `PerfectShape::Arc`, `PerfectShape::Ellipse`, `PerfectShape::Circle`, `PerfectShape::Rectangle`, and `PerfectShape::Square`. If a path is closed, its last point is automatically connected to its first point with a line segment. The winding rule can be `:wind_non_zero` (default) or `:wind_even_odd`. `line_to_complex_shapes` can be `true` or `false` (default), indicating whether to connect to complex shapes, meaning `Arc`, `Ellipse`, `Circle`, `Rectangle`, and `Square`, with a line, or otherwise move to their start point instead.

- `#shapes`: the shapes that the path is composed of (must always start with `PerfectShape::Point` or Array of `[x,y]` coordinates representing start point)

- `#basic_shapes`: the basic shapes that the path is composed of, meaning only `Point`, `Line`, `QuadraticBezierCurve`, and `CubicBezierCurve` shapes (decomposing complex shapes like `Arc`, `Ellipse`, `Circle`, `Rectangle`, and `Square`, using their `#to_path_shapes` method)

- `#closed?`: returns `true` if closed and `false` otherwise

- `#winding_rule`: returns winding rule (`:wind_non_zero` or `:wind_even_odd`)

- `#points`: path points calculated (derived) from shapes

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: When `outline` is `false`, it checks if point is inside path utilizing the configured winding rule, which can be the [Nonzero-Rule](https://en.wikipedia.org/wiki/Nonzero-rule) (aka [Winding Number Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon#Winding_number_algorithm)) or the [Even-Odd Rule](https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule) (aka [Ray Casting Algorithm](https://en.wikipedia.org/wiki/Point_in_polygon#Ray_casting_algorithm)). Otherwise, when `outline` is `true`, it checks if point is on the outline. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a path shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing

- `#point_crossings(x_or_point, y=nil)`: calculates the number of times the given path crosses the ray extending to the right from (x,y)

- `#disconnected_shapes`: Disconnected shapes have their start point filled in so that each shape does not depend on the previous shape to determine its start point. Also, if a point is followed by a non-point shape, it is removed since it is augmented to the following shape as its start point. Lastly, if the path is closed, an extra shape is added to represent the line connecting the last point to the first



Example:



```ruby

require 'perfect-shape'



path_shapes = []

path_shapes << PerfectShape::Point.new(x: 200, y: 150)

path_shapes << PerfectShape::Line.new(points: [250, 170]) # no need for start point, just end point

path_shapes << PerfectShape::QuadraticBezierCurve.new(points: [[300, 185], [350, 150]]) # no need for start point, just control point and end point

path_shapes << PerfectShape::CubicBezierCurve.new(points: [[370, 50], [430, 220], [480, 170]]) # no need for start point, just two control points and end point



shape = PerfectShape::Path.new(shapes: path_shapes, closed: false, winding_rule: :wind_non_zero)



shape.contain?(275, 165) # => true

shape.contain?([275, 165]) # => true

shape.contain?(275, 165, outline: true) # => false

shape.contain?([275, 165], outline: true) # => false

shape.contain?(shape.disconnected_shapes[1].curve_center_x, shape.disconnected_shapes[1].curve_center_y, outline: true) # => true

shape.contain?([shape.disconnected_shapes[1].curve_center_x, shape.disconnected_shapes[1].curve_center_y], outline: true) # => true

shape.contain?(shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y, outline: true) # => false

shape.contain?([shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y], outline: true) # => false

shape.contain?(shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y, outline: true, distance_tolerance: 1) # => true

shape.contain?([shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y], outline: true, distance_tolerance: 1) # => true

```



### `PerfectShape::CompositeShape`



Class



Extends `PerfectShape::Shape`



A composite shape is simply an aggregate of multiple shapes (e.g. square and triangle polygon)



![composite shape](https://raw.githubusercontent.com/AndyObtiva/perfect-shape/master/images/composite-shape.png)



- `::new(shapes: [])`: constructs a composite shape with `shapes` as `Array` of `PerfectShape::Shape` objects

- `#shapes`: the shapes that the composite shape is composed of

- `#min_x`: min x

- `#min_y`: min y

- `#max_x`: max x

- `#max_y`: max y

- `#width`: width (from min x to max x)

- `#height`: height (from min y to max y)

- `#center_point`: center point as `Array` of `[center_x, center_y]` coordinates

- `#center_x`: center x

- `#center_y`: center y

- `#bounding_box`: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)

- `#==(other)`: Returns `true` if equal to `other` or `false` otherwise

- `#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0)`: When `outline` is `false`, it checks if point is inside any of the shapes owned by the composite shape. Otherwise, when `outline` is `true`, it checks if point is on the outline of any of the shapes owned by the composite shape. `distance_tolerance` can be used as a fuzz factor when `outline` is `true`, for example, to help GUI users mouse-click-select a composite shape from its outline more successfully

- `#intersect?(rectangle)`: Returns `true` if intersecting with interior of rectangle or `false` otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing



Example:



```ruby

require 'perfect-shape'



shapes = []

shapes << PerfectShape::Square.new(x: 120, y: 215, length: 100)

shapes << PerfectShape::Polygon.new(points: [[120, 215], [170, 165], [220, 215]])



shape = PerfectShape::CompositeShape.new(shapes: shapes)



shape.contain?(170, 265) # => true inside square

shape.contain?([170, 265]) # => true inside square

shape.contain?(170, 265, outline: true) # => false

shape.contain?([170, 265], outline: true) # => false

shape.contain?(170, 315, outline: true) # => true

shape.contain?([170, 315], outline: true) # => true

shape.contain?(170, 316, outline: true) # => false

shape.contain?([170, 316], outline: true) # => false

shape.contain?(170, 316, outline: true, distance_tolerance: 1) # => true

shape.contain?([170, 316], outline: true, distance_tolerance: 1) # => true



shape.contain?(170, 190) # => true inside polygon

shape.contain?([170, 190]) # => true inside polygon

shape.contain?(170, 190, outline: true) # => false

shape.contain?([170, 190], outline: true) # => false

shape.contain?(145, 190, outline: true) # => true

shape.contain?([145, 190], outline: true) # => true

shape.contain?(145, 189, outline: true) # => false

shape.contain?([145, 189], outline: true) # => false

shape.contain?(145, 189, outline: true, distance_tolerance: 1) # => true

shape.contain?([145, 189], outline: true, distance_tolerance: 1) # => true

```



## Process



[Glimmer Process](https://github.com/AndyObtiva/glimmer/blob/master/PROCESS.md)



## Resources



- Rubydoc: https://www.rubydoc.info/gems/perfect-shape

- Point in Polygon: https://en.wikipedia.org/wiki/Point_in_polygon

- Even-Odd Rule: https://en.wikipedia.org/wiki/Even%E2%80%93odd_rule

- Nonzero Rule: https://en.wikipedia.org/wiki/Nonzero-rule

- IEEE 754-1985 Remainder: https://en.wikipedia.org/wiki/IEEE_754-1985



## TODO



[TODO.md](TODO.md)



## Change Log



[CHANGELOG.md](CHANGELOG.md)



## Contributing



-   Check out the latest master to make sure the feature hasn't been

    implemented or the bug hasn't been fixed yet.

-   Check out the issue tracker to make sure someone already hasn't

    requested it and/or contributed it.

-   Fork the project.

-   Start a feature/bugfix branch.

-   Commit and push until you are happy with your contribution.

-   Make sure to add tests for it. This is important so I don't break it

    in a future version unintentionally.

-   Please try not to mess with the Rakefile, version, or history. If

    you want to have your own version, or is otherwise necessary, that

    is fine, but please isolate to its own commit so I can cherry-pick

    around it.



## Copyright



[MIT](LICENSE.txt)



Copyright (c) 2021-2022 Andy Maleh. See

[LICENSE.txt](LICENSE.txt) for further details.