Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/averyanalex/quantpiler
Сompiler of classical algorithms into oracles for quantum computing
https://github.com/averyanalex/quantpiler
quantum-computing
Last synced: 2 months ago
JSON representation
Сompiler of classical algorithms into oracles for quantum computing
- Host: GitHub
- URL: https://github.com/averyanalex/quantpiler
- Owner: averyanalex
- License: agpl-3.0
- Created: 2023-07-12T15:58:11.000Z (over 1 year ago)
- Default Branch: main
- Last Pushed: 2024-06-25T18:37:14.000Z (7 months ago)
- Last Synced: 2024-10-12T00:31:58.292Z (3 months ago)
- Topics: quantum-computing
- Language: Rust
- Homepage:
- Size: 460 KB
- Stars: 10
- Watchers: 2
- Forks: 2
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
[](https://github.com/averyanalex/quantpiler/actions/workflows/ci.yml)
[](https://opensource.org/license/agpl-v3)
[](https://pypi.org/project/quantpiler/)
# Сompiler of classical algorithms into oracles for quantum computing
## Achievements:
- CRC32 hash function (4 byte input) - 116 qubits.
## Architecture:
1. Building expression.
2. Optimizing expression.
3. Constructing list of logical gates (logical expressions) for each bit of
optimized expression.
4. Logical gates optimization (minimizing unique logic operations and qubit
allocations).
5. Generation of a quantum circuit from a DAG of logical gates.
## Authors:
- Alexander Averyanov - author
- Evgeny Kiktenko - mentor
- Dmitry Ershov - helped with the optimizer design
## Example:
```python
import quantpiler
x_len = 4
x = quantpiler.argument("x", x_len)
a = 6
# N = 2**4
prod = 1
for i in range(x_len):
prod = ((x >> i) & 1).ternary(prod * a**(2**i), prod) & 0b1111
circ = prod.compile()
qc = quantpiler.circuit_to_qiskit(circ)
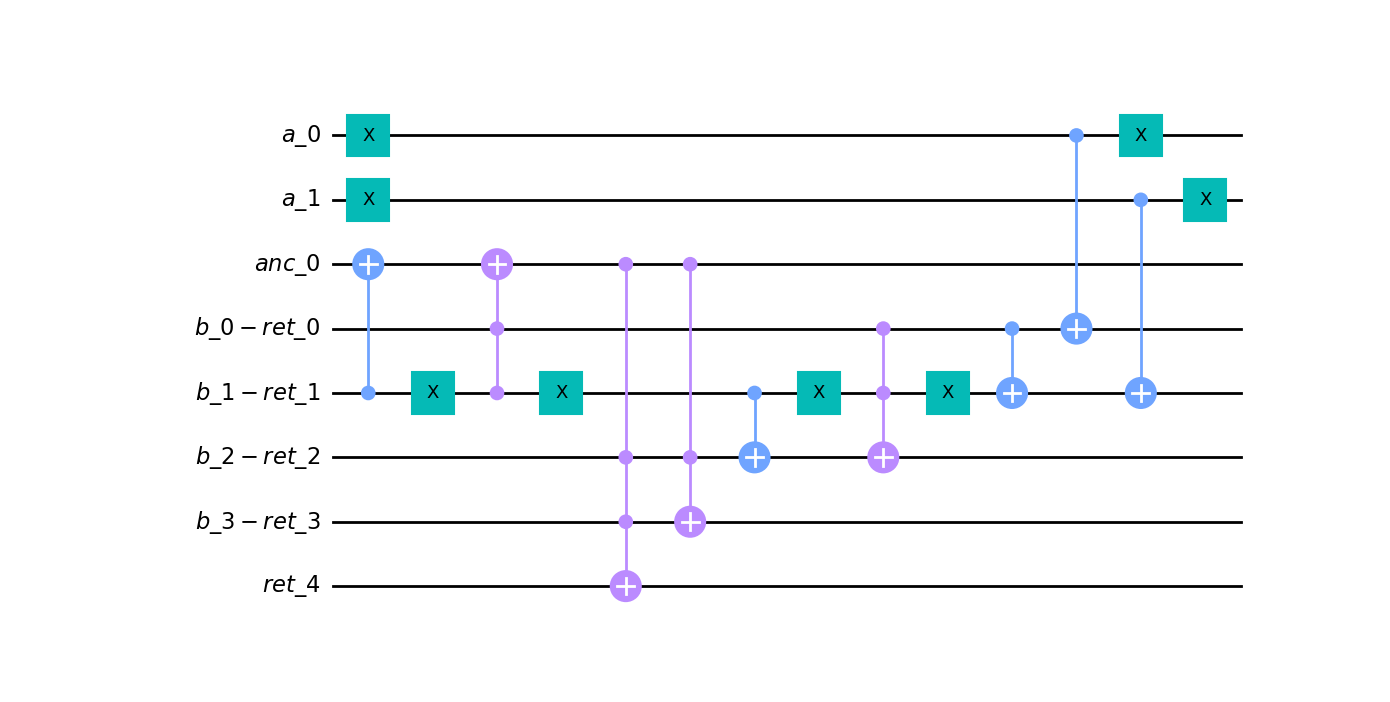
qc.draw("mpl")
```
```python
# returning ancillas and arguments to their original state
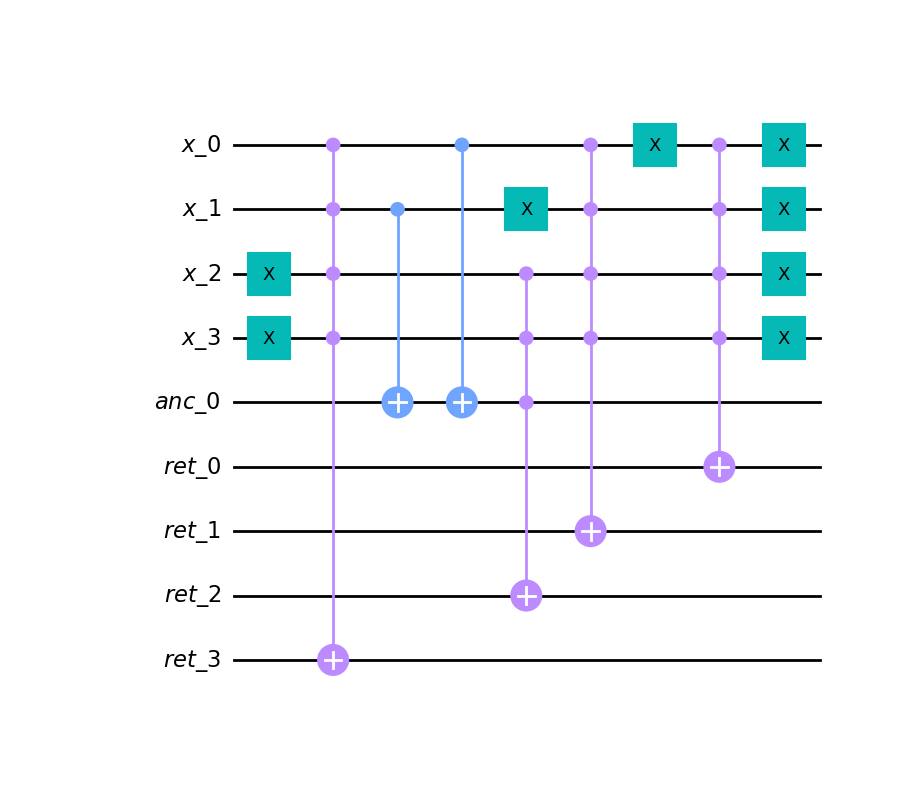
rqc = quantpiler.circuit_to_qiskit(circ, rev=True)
rqc.draw("mpl")
```
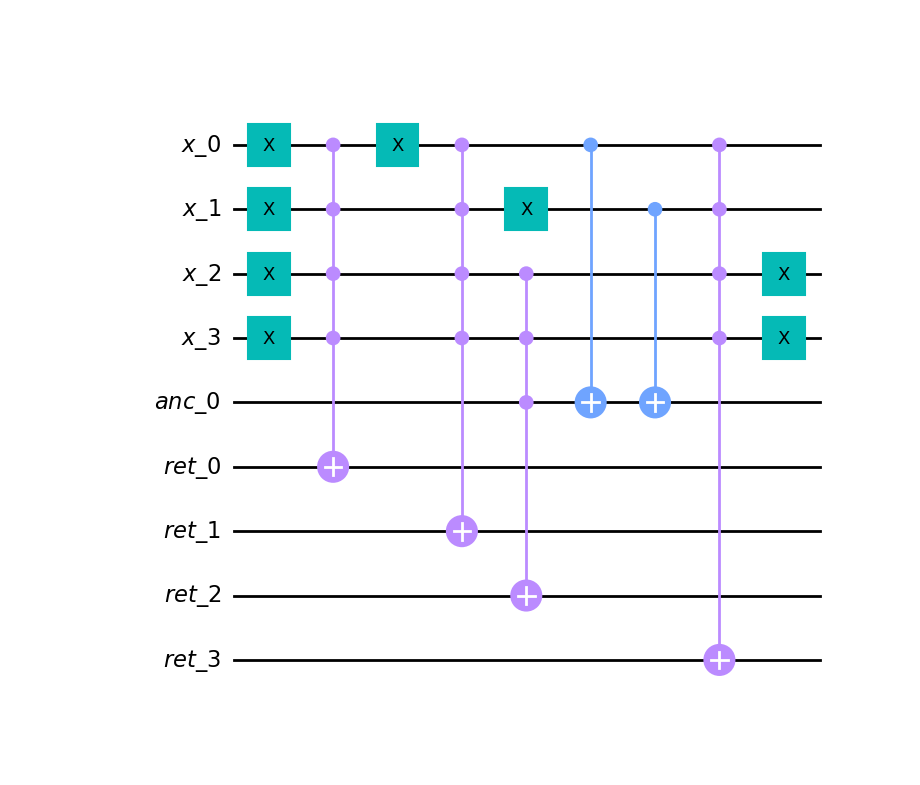
## User guide
### Installation
```shell
pip install quantpiler
```
Binary releases on PyPI only available for Windows (x86, x86_64) and
GNU/Linux (x86_64).
Now you can import library in Python:
```python
import quantpiler
```
### Creating input variables
```python
a = quantpiler.argument("a", 2)
b = quantpiler.argument("b", 4)
```
This will create argument "a" with length of 2 qubits and "b" with length of 4
qubits. You can't use arguments with same name but with
different lengths.
### Expressions
Any argument variable, constant, or combination thereof is an expression.
Expressions are actually lists of logic gates representing each bit. For
example, `a ^ b` is effectively `[[a[0] ^ b[0], [a[1] ^ b[1], b[2], b[3]]`.
#### Output expression lengths
Let's `a` -- length of first operand, `b` -- length (value for bitshifts) of
second operand.
| Name | Notation | Length |
| -------------- | -------- | ------------- |
| Binary invert | ~ | a |
| Bitwise XOR | ^ | max(a, b) |
| Bitwise OR | \| | max(a, b) |
| Bitwise AND | & | min(a, b) |
| Sum | + | max(a, b) + 1 |
| Product | \* | a + b |
| Right bitshift | >> | a - b |
| Left bitshift | << | a + b |
Length is the **maximum possible** length of result. Actual length depends on
optimizer decitions: for example, the length of `a ^ a` will be 0 (no qubits,
empty expression).
#### Estimating length of expression:
```python
# you can use builtin python's len to get estimated expression's length
length = len(a ^ b + 1)
```
Please note that this is an **estimated** length as actual length may vary depending
optimizer solutions.
#### Debugging expression:
```python
print(str(a ^ b + 1))
```
or, for jupyter:
```python
a ^ b + 1
```
This will print `(^ "a(2)" (+ 1 "4(2)"))` for `a` of length 2 and `b` of length 4.
### Bitwise binary operations
```python
r = ~a
r = a ^ b
r = a | b
r = a & b
```
You can also do this with constants:
```python
r = 0b101 ^ a
b |= 1
r = b & 0b11
```
### Bit shifting
```python
r = a << 2
r = b >> 3
```
Please note that only constant distance shifting is supported at this time.
### Arithmetic operations
```python
r = a + b
r = 2 * a * b
```
### Ternary operations
If you want to emulate if statements, i.e.
```python
if cond:
r = a + b
else:
r = b & 0b11
```
you can use ternary operators:
```python
r = cond.ternary(a + b, b & 0b11)
```
Note that cond must be an expression exactly 1 qubit long. You can
achieve this by using bitwise and with 1.
### Compiling
Let's compile something:
```python
r = a ^ b + 3
# internal circuit representation
circ = r.compile()
# QuantumCircuit from qiskit
qc = quantpiler.circuit_to_qiskit(circ)
# let's draw our circuit
qc.draw("mpl")
```
