https://github.com/benruijl/symbolica
A modern computer algebra library for Python and Rust.
https://github.com/benruijl/symbolica
arithmetic computer-algebra expansion expressions factorization greatest-common-divisor groebner-basis mathematics numerical-integration pattern-matching physics polynomial-arithmetic symbolic-computation symbolic-manipulation
Last synced: about 1 month ago
JSON representation
A modern computer algebra library for Python and Rust.
- Host: GitHub
- URL: https://github.com/benruijl/symbolica
- Owner: benruijl
- License: other
- Created: 2023-01-11T14:43:12.000Z (over 2 years ago)
- Default Branch: main
- Last Pushed: 2025-04-08T08:48:29.000Z (2 months ago)
- Last Synced: 2025-04-13T01:55:33.922Z (2 months ago)
- Topics: arithmetic, computer-algebra, expansion, expressions, factorization, greatest-common-divisor, groebner-basis, mathematics, numerical-integration, pattern-matching, physics, polynomial-arithmetic, symbolic-computation, symbolic-manipulation
- Language: Rust
- Homepage: https://symbolica.io
- Size: 3.52 MB
- Stars: 598
- Watchers: 13
- Forks: 27
- Open Issues: 3
-
Metadata Files:
- Readme: Readme.md
- Contributing: Contributing.md
- License: License.md
Awesome Lists containing this project
README

# Symbolica ⊆ Modern Computer Algebra
Symbolica is a blazing fast computer algebra system for Python and Rust, born of a need to push the boundaries of computations in science and enterprise.
Check out the live [Jupyter Notebook demo](https://colab.research.google.com/drive/1VAtND2kddgBwNt1Tjsai8vnbVIbgg-7D?usp=sharing)!
For documentation and more, see [symbolica.io](https://symbolica.io).
## Quick Example
Symbolica allows you to build and manipulate mathematical expressions, for example from a Jupyter Notebook:

You are able to perform these operations from the comfort of a programming language that you (probably) already know, by using Symbolica's bindings to Python and Rust:
# Installation
Visit the [Get Started](https://symbolica.io/docs/get_started.html) page for detailed installation instructions.
## Python
Symbolica can be installed for Python >3.5 using `pip`:
```sh
pip install symbolica
```
## Rust
If you want to use Symbolica as a library in Rust, simply include it in the `Cargo.toml`:
```toml
[dependencies]
symbolica = "0.16"
```
# Examples
Below we list some examples of the features of Symbolica. Check the [guide](https://symbolica.io/docs/) for a complete overview.
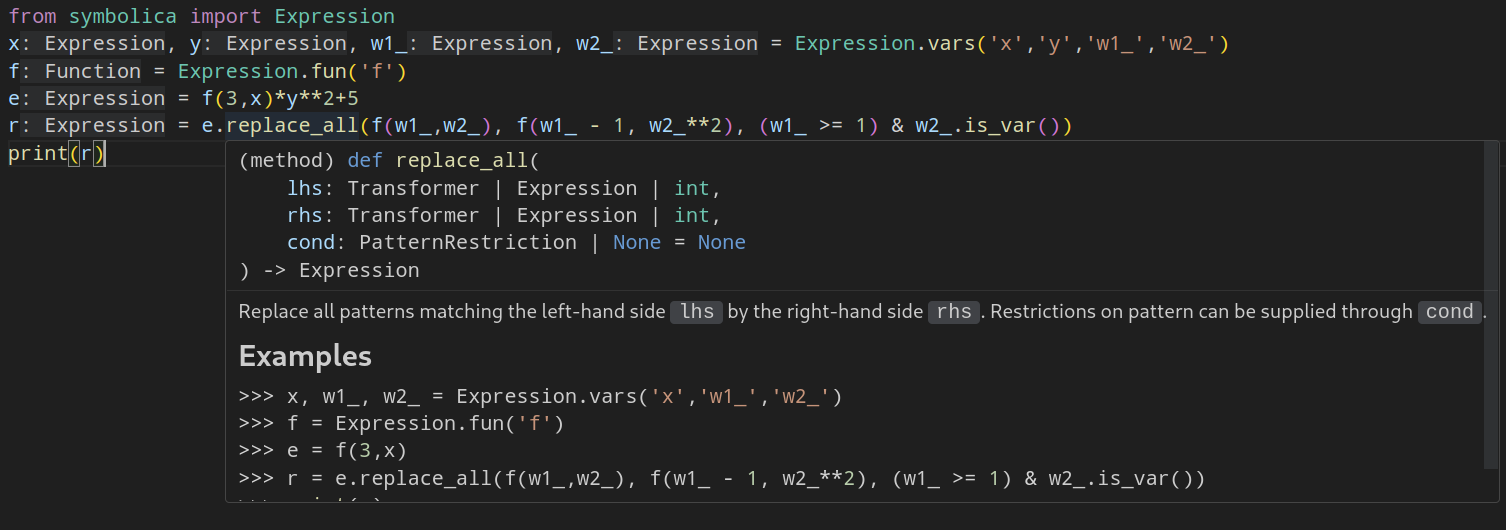
### Pattern matching
Variables ending with a `_` are wildcards that match to any subexpression.
In the following example we try to match the pattern `f(w1_,w2_)`:
```python
from symbolica import *
x, y, w1_, w2_, f = S('x','y','w1_','w2_', 'f')
e = f(3,x)*y**2+5
r = e.replace_all(f(w1_,w2_), f(w1_ - 1, w2_**2))
print(r)
```
which yields `y^2*f(2,x^2)+5`.
### Solving a linear system
Solve a linear system in `x` and `y` with a parameter `c`:
```python
from symbolica import *
x, y, c, f = S('x', 'y', 'c', 'f')
x_r, y_r = Expression.solve_linear_system(
[f(c)*x + y + c, y + c**2], [x, y])
print('x =', x_r, ', y =', y_r)
```
which yields `x = (-c+c^2)*f(c)^-1` and `y = -c^2`.
### Series expansion
Perform a series expansion in `x`:
```python
from symbolica import *
e = E('exp(5+x)/(1-x)').series(S('x'), 0, 3)
print(e)
```
which yields `(exp(5))+(2*exp(5))*x+(5/2*exp(5))*x^2+(8/3*exp(5))*x^3+𝒪(x^4)`.
### Rational arithmetic
Symbolica is world-class in rational arithmetic, outperforming Mathematica, Maple, Form, Fermat, and other computer algebra packages. Simply convert an expression to a rational polynomial:
```python
from symbolica import *
p = E('(x*y^2*5+5)^2/(2*x+5)+(x+4)/(6*x^2+1)').to_rational_polynomial()
print(p)
```
which yields `(45+13*x+50*x*y^2+152*x^2+25*x^2*y^4+300*x^3*y^2+150*x^4*y^4)/(5+2*x+30*x^2+12*x^3)`.
## Development
Follow the development and discussions on [Zulip](https://reform.zulipchat.com)!



