Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/bifurcationkit/BifurcationKit.jl
A Julia package to perform Bifurcation Analysis
https://github.com/bifurcationkit/BifurcationKit.jl
bifurcation bifurcation-diagram codim2 continuation deflation floquet gpu hopf-point newton-krylov pde periodic-orbits pseudo-arclength-continuation
Last synced: 3 months ago
JSON representation
A Julia package to perform Bifurcation Analysis
- Host: GitHub
- URL: https://github.com/bifurcationkit/BifurcationKit.jl
- Owner: bifurcationkit
- License: other
- Created: 2019-01-23T16:32:05.000Z (almost 6 years ago)
- Default Branch: master
- Last Pushed: 2023-12-18T21:10:08.000Z (11 months ago)
- Last Synced: 2023-12-19T13:24:24.401Z (11 months ago)
- Topics: bifurcation, bifurcation-diagram, codim2, continuation, deflation, floquet, gpu, hopf-point, newton-krylov, pde, periodic-orbits, pseudo-arclength-continuation
- Language: Julia
- Homepage: https://bifurcationkit.github.io/BifurcationKitDocs.jl/stable
- Size: 100 MB
- Stars: 268
- Watchers: 13
- Forks: 33
- Open Issues: 20
-
Metadata Files:
- Readme: README.md
- License: LICENSE.md
- Citation: CITATION.bib
- Authors: AUTHORS
Awesome Lists containing this project
- awesome-sciml - rveltz/BifurcationKit.jl: A Julia package to perform Bifurcation Analysis
README
# BifurcationKit.jl
| **Documentation** | **Build Status** | **Coverage** | **Version** |
| :-: | :-: | :-: | :-: |
| [![][docs-stable-img]][docs-stable-url] | | [](https://codecov.io/gh/bifurcationkit/BifurcationKit.jl) | [![ver-img]][ver-url] |
| [![][docs-dev-img]][docs-dev-url] | [](https://github.com/rveltz/BifurcationKit.jl/actions) | [](https://pkgs.genieframework.com?packages=BifurcationKit) | [![deps-img]][deps-url] |
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://bifurcationkit.github.io/BifurcationKitDocs.jl/stable
[docs-dev-img]: https://img.shields.io/badge/docs-dev-purple.svg
[docs-dev-url]: https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev
[ver-img]: https://juliahub.com/docs/BifurcationKit/version.svg
[ver-url]: https://juliahub.com/ui/Packages/BifurcationKit/UDEDl
[deps-img]: https://juliahub.com/docs/General/BifurcationKit/stable/deps.svg
[deps-url]: https://juliahub.com/ui/Packages/General/BifurcationKit?t=2
This Julia package aims at performing **automatic bifurcation analysis** of possibly large dimensional equations F(u, λ)=0 where λ is real by taking advantage of iterative methods, dense / sparse formulation and specific hardwares (*e.g.* GPU).
It incorporates continuation algorithms (PALC, deflated continuation, ...) based on a Newton-Krylov method to correct the predictor step and a Matrix-Free/Dense/Sparse eigensolver is used to compute stability and bifurcation points.
> The idea is to be able to seamlessly switch the continuation algorithm a bit like changing the time stepper (Euler, RK4,...) for ODEs.
`BifurcationKit` can also seek for [periodic orbits](https://bifurcationkit.github.io/BifurcationKitDocs.jl/stable/periodicOrbit/) of Cauchy problems. **It is by now, one of the only software which provides shooting methods *and* methods based on finite differences / collocation to compute periodic orbits.**
The current focus is on large scale nonlinear problems and multiple hardwares. Hence, the goal is to provide Matrix Free methods on **GPU** (see [PDE example](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorials2b/#The-Swift-Hohenberg-equation-on-the-GPU-(non-local)-1) and [Periodic orbit example](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorialsCGL/#Continuation-of-periodic-orbits-on-the-GPU-(Advanced)-1)) or on **cluster** to study non linear PDE, nonlocal problems, compute sub-manifolds...
> Despite this focus, the package can easily handle low dimensional problems and specific optimizations are regularly added.
## Support and citation
If you use `BifurcationKit.jl` in your work, we ask that you cite the following paper. Open source development as part of academic research strongly depends on this. Please also consider starring this repository if you like our work, this will help us to secure funding in the future. It is referenced on HAL-Inria as follows:
```
@misc{veltz:hal-02902346,
TITLE = {{BifurcationKit.jl}},
AUTHOR = {Veltz, Romain},
URL = {https://hal.archives-ouvertes.fr/hal-02902346},
INSTITUTION = {{Inria Sophia-Antipolis}},
YEAR = {2020},
MONTH = Jul,
KEYWORDS = {pseudo-arclength-continuation ; periodic-orbits ; floquet ; gpu ; bifurcation-diagram ; deflation ; newton-krylov},
PDF = {https://hal.archives-ouvertes.fr/hal-02902346/file/354c9fb0d148262405609eed2cb7927818706f1f.tar.gz},
HAL_ID = {hal-02902346},
HAL_VERSION = {v1},
}
```
## Installation
This package requires Julia >= v1.3.0
To install it, please run
`] add BifurcationKit`
To install the bleeding edge version, please run
`] add BifurcationKit#master`
## Plugins
Most plugins are located in the organization [bifurcationkit](https://github.com/bifurcationkit):
- [HclinicBifurcationKit.jl](https://github.com/bifurcationkit/HclinicBifurcationKit.jl) bifurcation analysis of homoclinic / heteroclinic orbits of ordinary differential equations (ODE)
- [DDEBifurcationKit.jl](https://github.com/bifurcationkit/DDEBifurcationKit.jl) bifurcation analysis of delay differential equations (DDE)
- [AsymptoticNumericalMethod.jl](https://github.com/bifurcationkit/AsymptoticNumericalMethod.jl) provides the numerical continuation algorithm **Asymptotic Numerical Method** (ANM) which can be used directly in `BifurcationKit.jl`
- [GridapBifurcationKit.jl](https://github.com/bifurcationkit/GridapBifurcationKit) bifurcation analysis of PDEs solved with the Finite Elements Method (FEM) using the package [Gridap.jl](https://github.com/gridap/Gridap.jl).
- [PeriodicSchurBifurcationKit.jl](https://github.com/bifurcationkit/PeriodicSchurBifurcationKit.jl) state of the art computation of Floquet coefficients, useful for computing the stability of periodic orbits.
## Overview of capabilities
The list of capabilities is available [here](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/capabilities/).
## Examples of bifurcation diagrams (ODEs and PDEs)
|  |  |
|:-------------:|:-------------:|
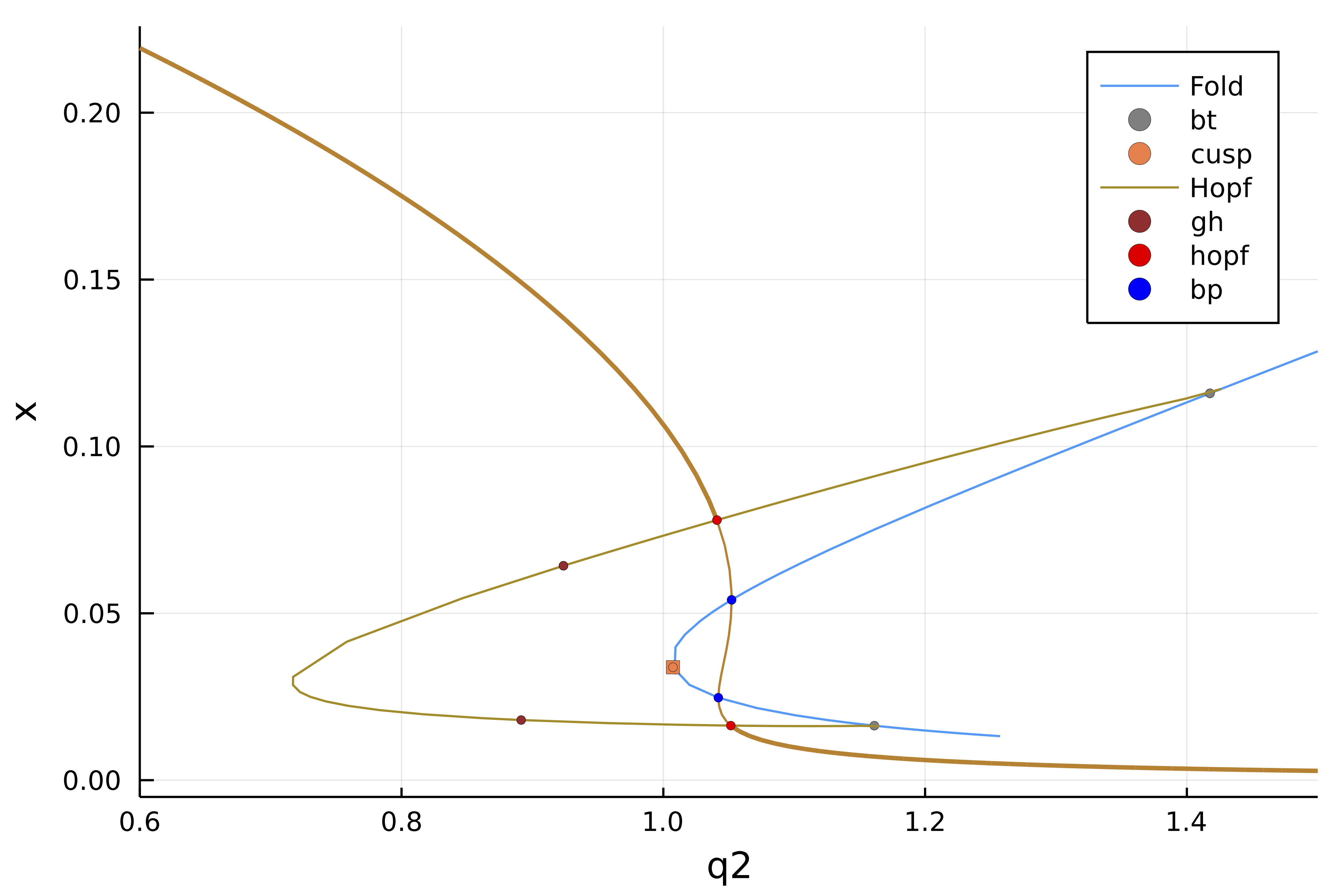| [simple ODE example](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/ode/tutorialsODE/#Neural-mass-equation-(Hopf-aBS)) | [Codimension 2 (ODE)](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/ode/tutorialCO/#CO-oxydation-(codim-2)) |
|  |  |
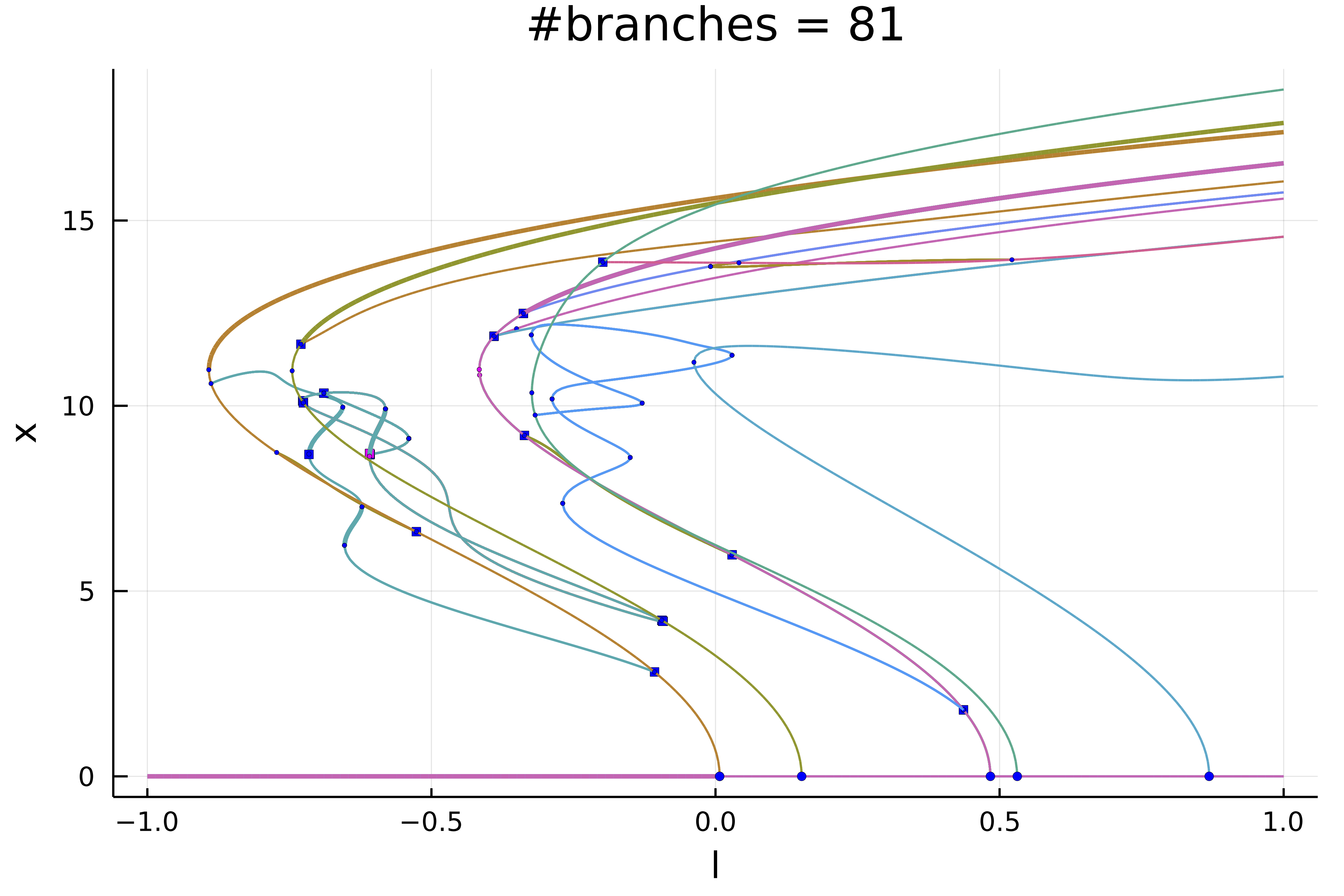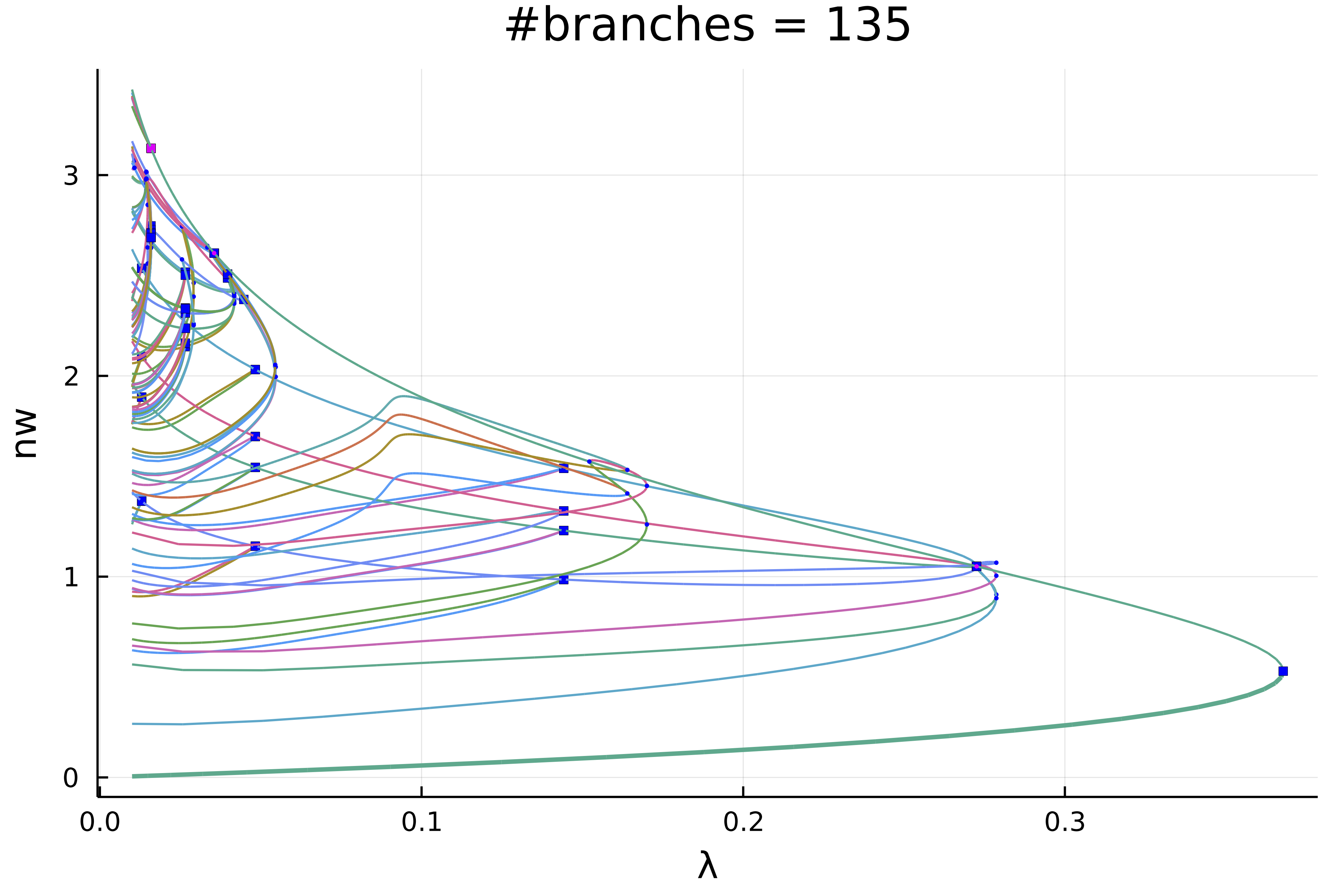| [Automatic Bif. Diagram in 1D Swift Hohenberg](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/Swift-Hohenberg1d/#d-Swift-Hohenberg-equation-(Automatic)) | [Automatic Bif. Diagram in 2D Bratu](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/mittelmannAuto/#Automatic-diagram-of-2d-Bratu–Gelfand-problem-(Intermediate)) |
|  |  |
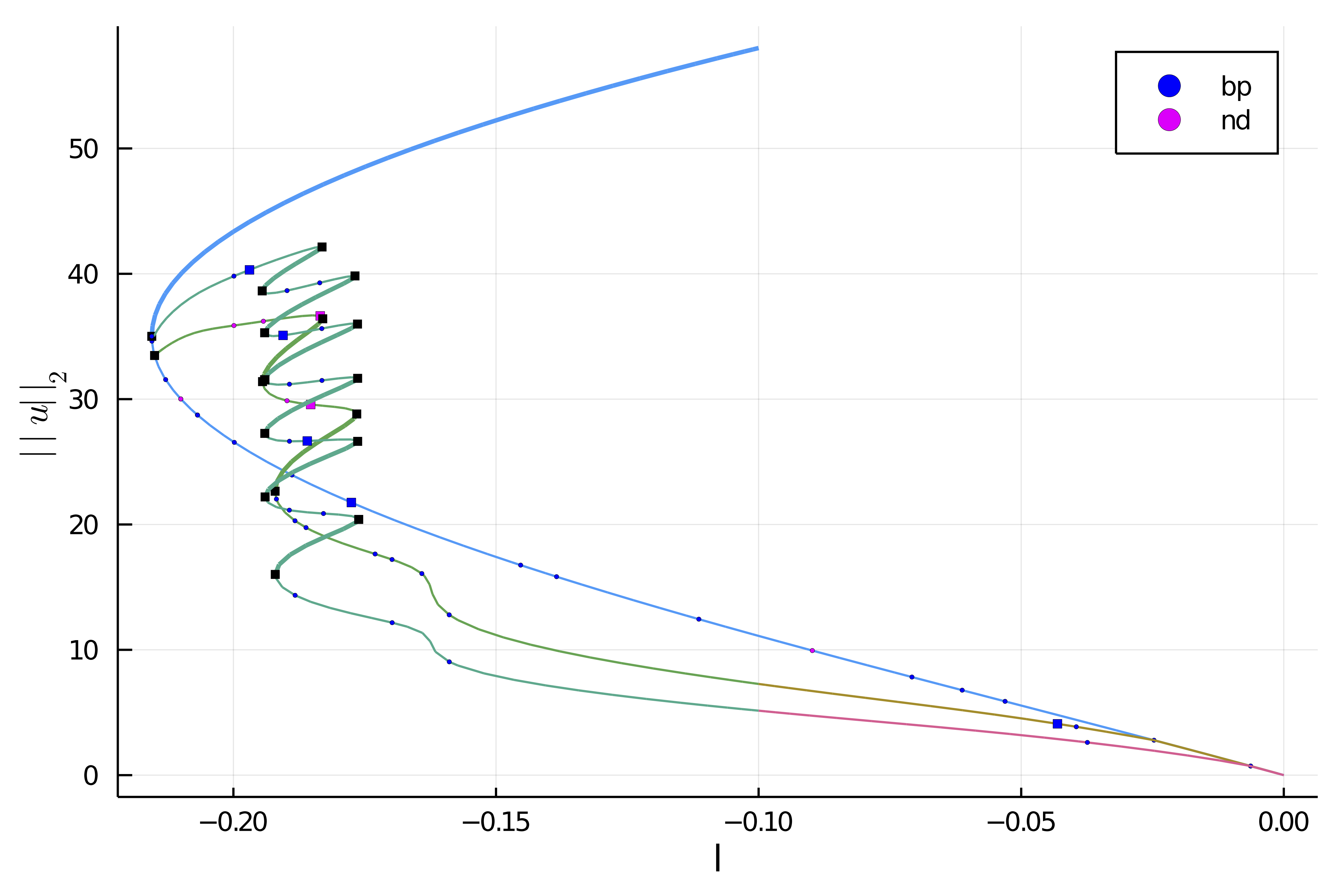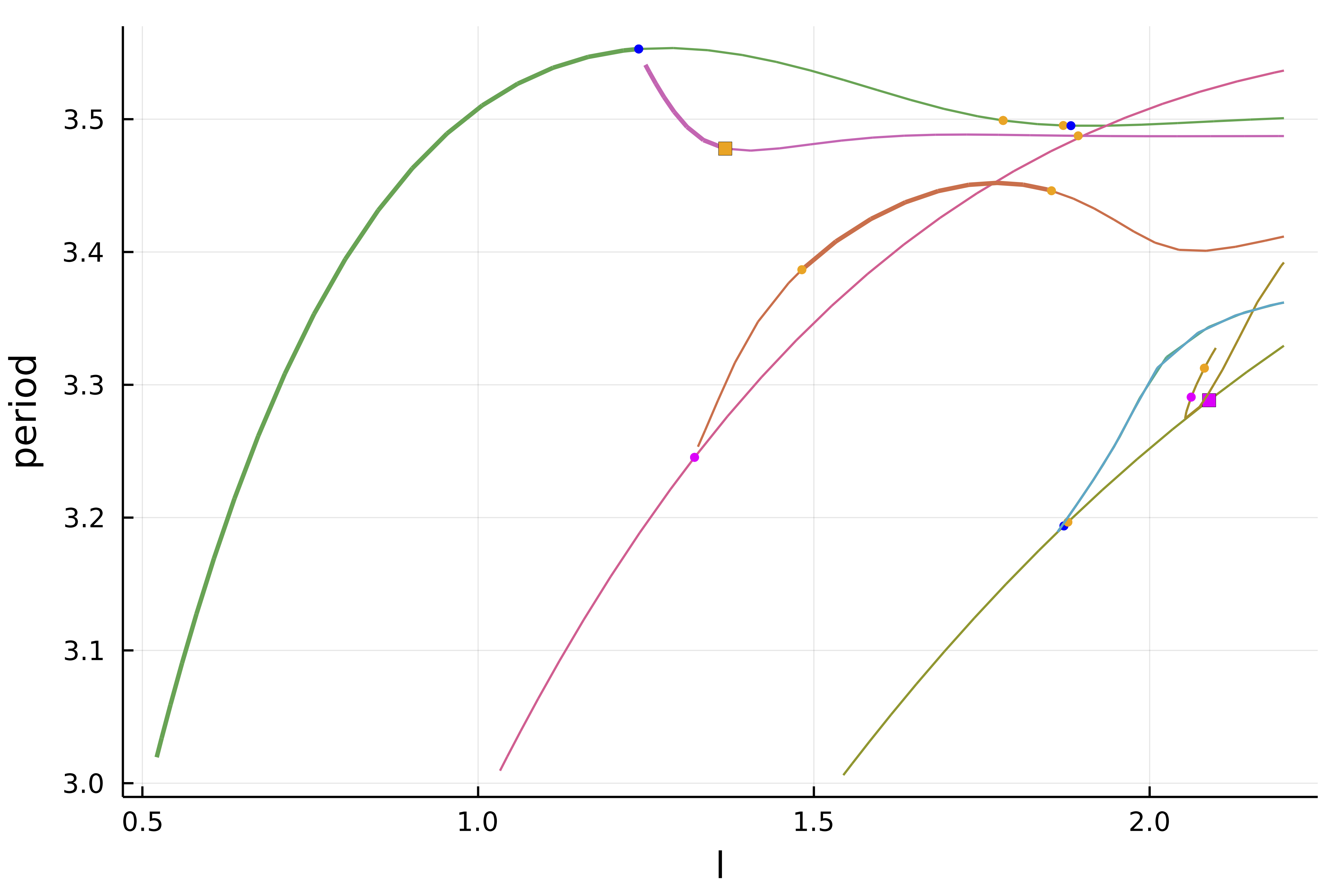| [Snaking in 2D Swift Hohenberg](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorials2/#d-Swift-Hohenberg-equation:-snaking,-Finite-Differences) | [Periodic orbits in 1D Brusselator](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorials3/#d-Brusselator-(automatic))
|  | |
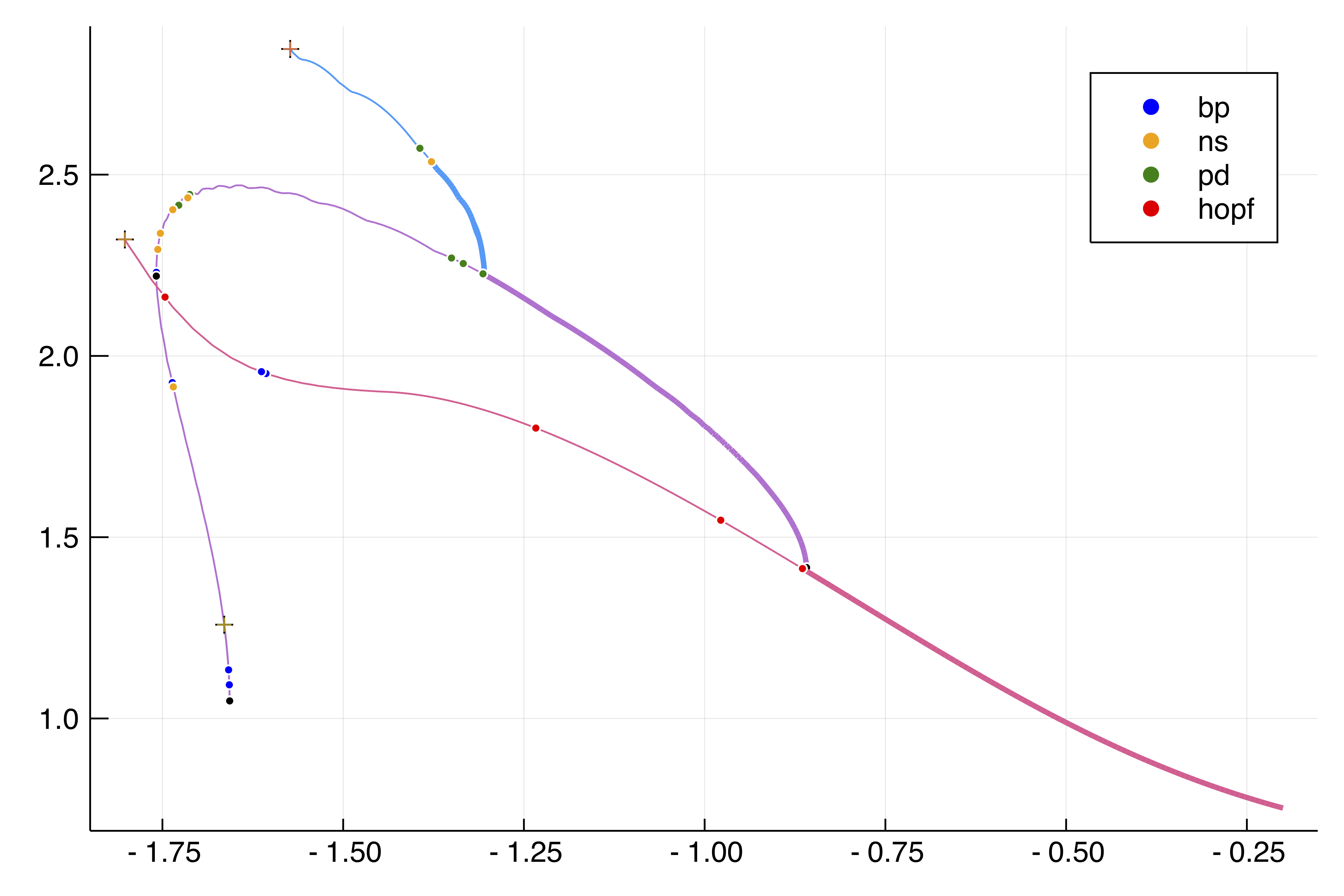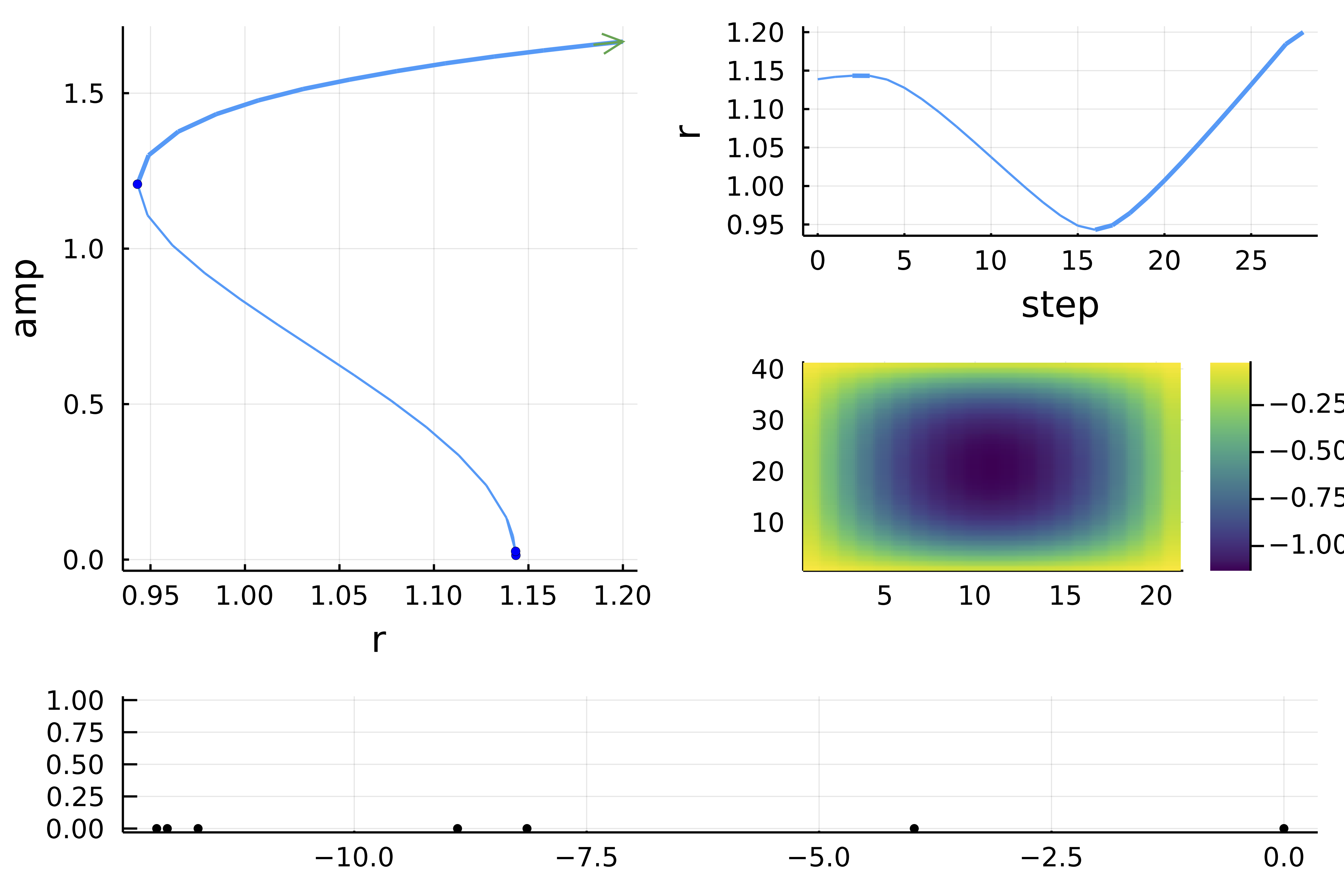| [Period doubling BVAM Model](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorialsPD/#Period-doubling-in-the-Barrio-Varea-Aragon-Maini-model) | [Periodic orbits in 2D Ginzburg-Landau](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorialsCGL/#d-Ginzburg-Landau-equation-(finite-differences)) |
|  |  |
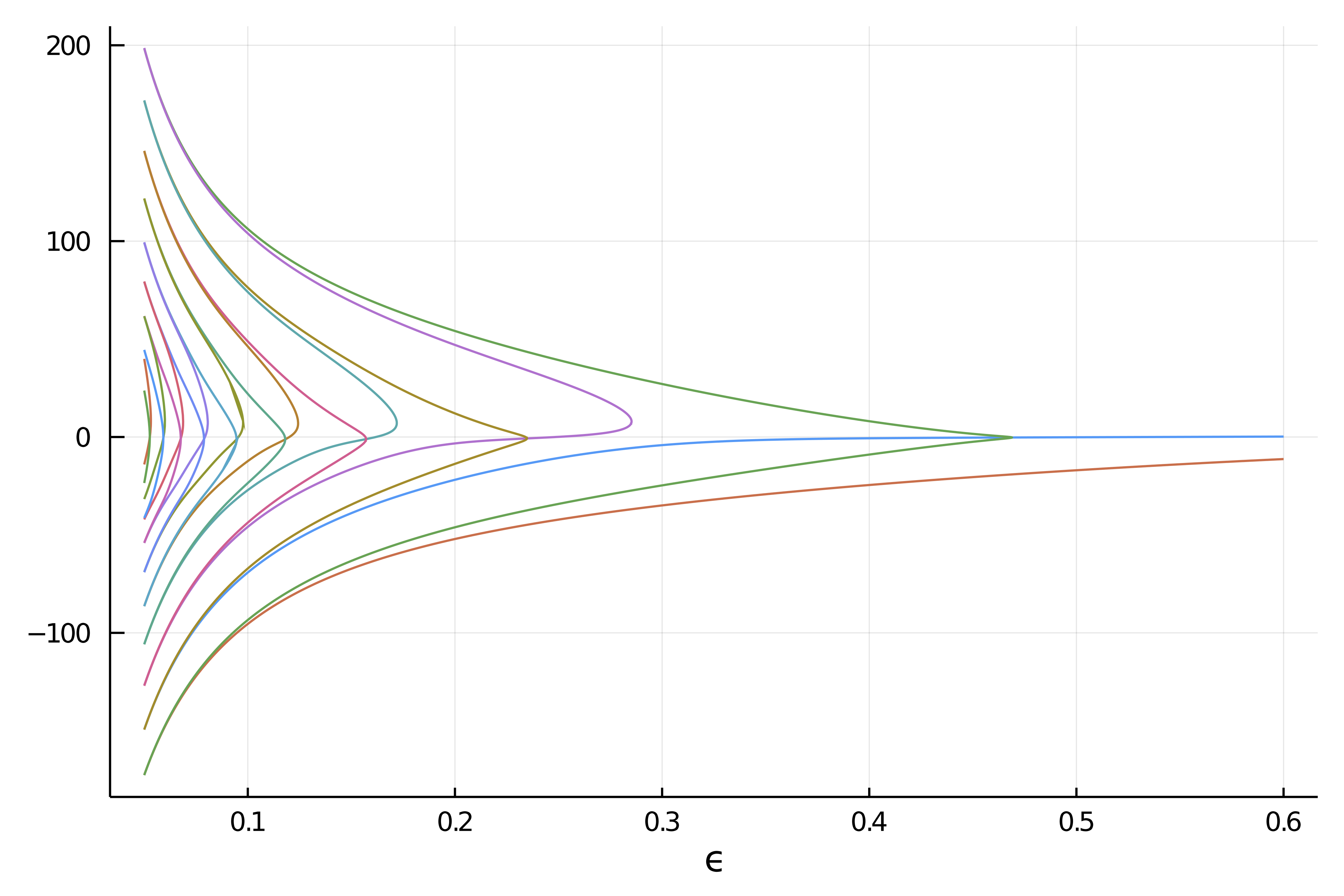| [Deflated Continuation in Carrier problem](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorialCarrier/#Deflated-Continuation-in-the-Carrier-Problem) | [2D Swift Hohenberg on GPU](https://bifurcationkit.github.io/BifurcationKitDocs.jl/dev/tutorials/tutorials2b/#d-Swift-Hohenberg-equation-(non-local)-on-the-GPU,-periodic-BC-(Advanced)) |