https://github.com/cduck/feynman_path
Visualization tool for the Feynman Path Integral applied to quantum circuits
https://github.com/cduck/feynman_path
feynman-integrals path-integral quantum-computing visualization
Last synced: 9 months ago
JSON representation
Visualization tool for the Feynman Path Integral applied to quantum circuits
- Host: GitHub
- URL: https://github.com/cduck/feynman_path
- Owner: cduck
- License: mit
- Created: 2021-03-24T03:42:47.000Z (almost 5 years ago)
- Default Branch: master
- Last Pushed: 2023-02-26T10:53:51.000Z (almost 3 years ago)
- Last Synced: 2024-11-09T08:07:19.828Z (about 1 year ago)
- Topics: feynman-integrals, path-integral, quantum-computing, visualization
- Language: Python
- Homepage:
- Size: 531 KB
- Stars: 51
- Watchers: 4
- Forks: 14
- Open Issues: 3
-
Metadata Files:
- Readme: README.md
- License: LICENSE.txt
Awesome Lists containing this project
README
# Feynman Path Sum Diagram for Quantum Circuits
A visualization tool for the Feynman Path Sum applied to quantum circuits.
The [path integral formulation](https://en.wikipedia.org/wiki/Path_integral_formulation) is an interpretation of quantum mechanics that can aid in understanding superposition and interference.
Path sum:
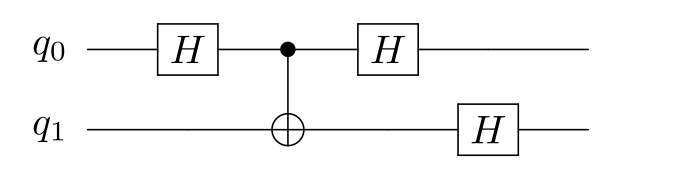
Circuit diagram:

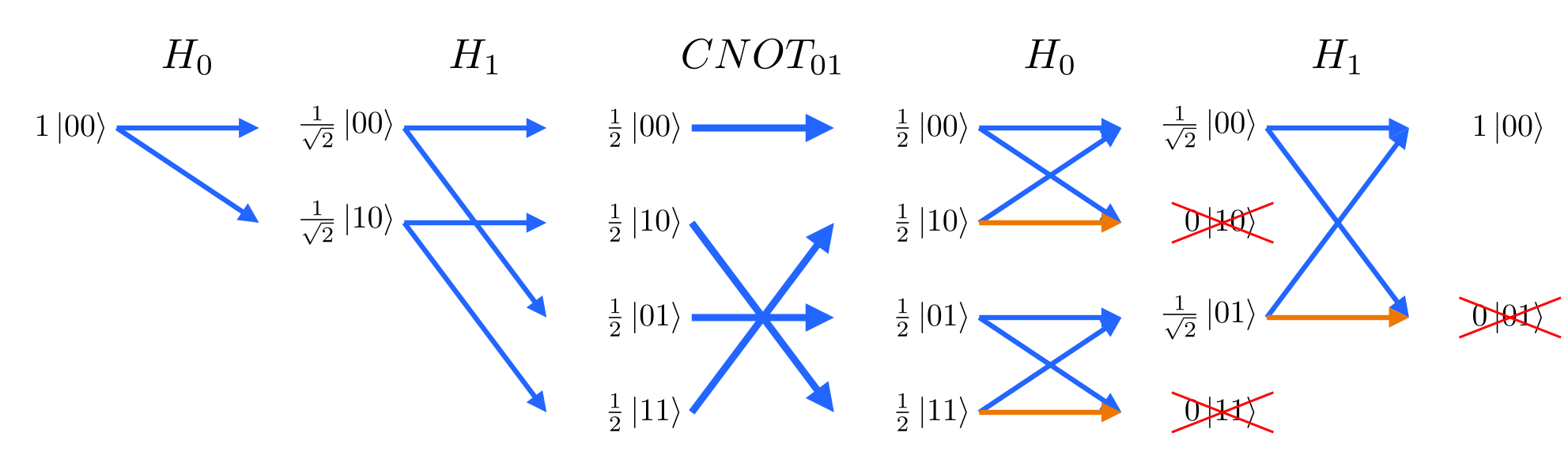
How to read a path sum diagram:
- Time flows from left to right as gates are executed on qubits.
- Arrows transition from one state to another and traversing the arrows gives a path to an output.
- Two diverging arrows indicate a split into two potential outcomes.
- An orange arrow indicates a negative sign is added to that outcome.
- When two arrows converge, the amplitudes are summed.
- Quantum interference is when positive and negative amplitudes cancel in this sum.
- The rightmost column lists the possible measurement outcomes along with the final probability amplitudes of measuring each outcome.
See also: [Bloch sphere visualization](https://github.com/cduck/bloch_sphere)
# Install
feynman\_path is available on PyPI:
```bash
python3 -m pip install feynman_path
```
## Prerequisites
Several non-python tools are used to generate the graphics and various output formats.
These non-python dependencies are listed below and platform-specific installation instructions can be found [here](https://github.com/cduck/latextools/#prerequisites).
- LaTeX: A distribution of LaTeX that provides the `pdflatex` command needs to be installed separately. Used to generate the gate and state labels.
- [pdf2svg](https://github.com/dawbarton/pdf2svg): Used to convert the LaTeX expressions into SVG elements.
- [Inkscape](https://inkscape.org/) (optional): Only required to convert the output to PDF format.
- [Cairo](https://www.cairographics.org/download/) (optional): Only required to convert the output to PNG format.
### Ubuntu
```bash
sudo apt install texlive pdf2svg inkscape libcairo2 # Or texlive-latex-recommended, or texlive-latex-extra
```
### macOS
Using [homebrew](https://brew.sh/):
```bash
brew install --cask mactex inkscape
brew install pdf2svg cairo
```
# Usage
This package provides a command line tool to generate diagrams.
### Examples
```bash
feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1
```
```bash
feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1 --circuit
```

### Command line options
```
$ feynman_path -h
usage: feynman_path [-h] [--svg] [--png] [--pdf] [--sequence] [--circuit]
[--scale SCALE] [--verbose]
name n_qubits gate [gate ...]
Renders a Feynman path sum diagram for a sequence of quantum gates.
positional arguments:
name The file name to save (excluding file extension)
n_qubits The number of qubits in the quantum circuit
gate List of gates to apply (e.g. h0 z1 cnot0,1)
optional arguments:
-h, --help show this help message and exit
--svg Save diagram as an SVG image (default)
--png Save diagram as a PNG image
--pdf Save diagram as a PDF document
--sequence Save a sequence of images that build up the diagram from left
to right as -nn.svg/png/pdf
--circuit Save a standard quantum circuit diagram named
-circuit.svg/png/pdf instead of a Feynman path diagram
--scale SCALE Scales the resolution of the diagram when saved as a PNG
--verbose Print extra progress information
```
### Python Package
feynman\_path also provides a Python 3 package as an alternative to the command line tool. Diagrams can be viewed directly in a Jupyter notebook or saved.
```python
import feynman_path
n_qubits = 3
font = 12
ws_label = 4+0.55*n_qubits # Label width relative to font size
w_time = 60+ws_label*font # Diagram column width
f = feynman_path.Diagram(
n_qubits, font=font, ws_label=ws_label, w_time=w_time)
f.perform_h(0)
f.perform_cnot(0, 1)
f.perform_z(1)
f.perform_cnot(1, 2, pre_latex=r'\color{red!80!black}')
f.perform_h(0)
f.perform_h(1)
f.perform_cnot(1, 0)
f.draw() # Display in Jupyter
```
```python
f.draw().save_svg('output.svg') # Save SVG
f.draw().set_pixel_scale(2).save_png('output.png') # Save PNG
import latextools
latextools.svg_to_pdf(f.draw()).save('output.pdf') # Save PDF
```
See [examples/render\_examples.py](https://github.com/cduck/feynman_path/blob/master/examples/render_examples.py) for more example code.
# Examples
### Using the CNOT gate to entangle qubits
The [CNOT gate](https://en.wikipedia.org/wiki/Controlled_NOT_gate) (⋅–⨁) can be used to entangle two qubits, creating a [Bell pair](https://en.wikipedia.org/wiki/Bell_state), but for certain input qubit states, the CNOT will have no effect.
**Create a Bell pair by using a CNOT on the |+0⟩ state (q0=|+⟩, q1=|0⟩):**
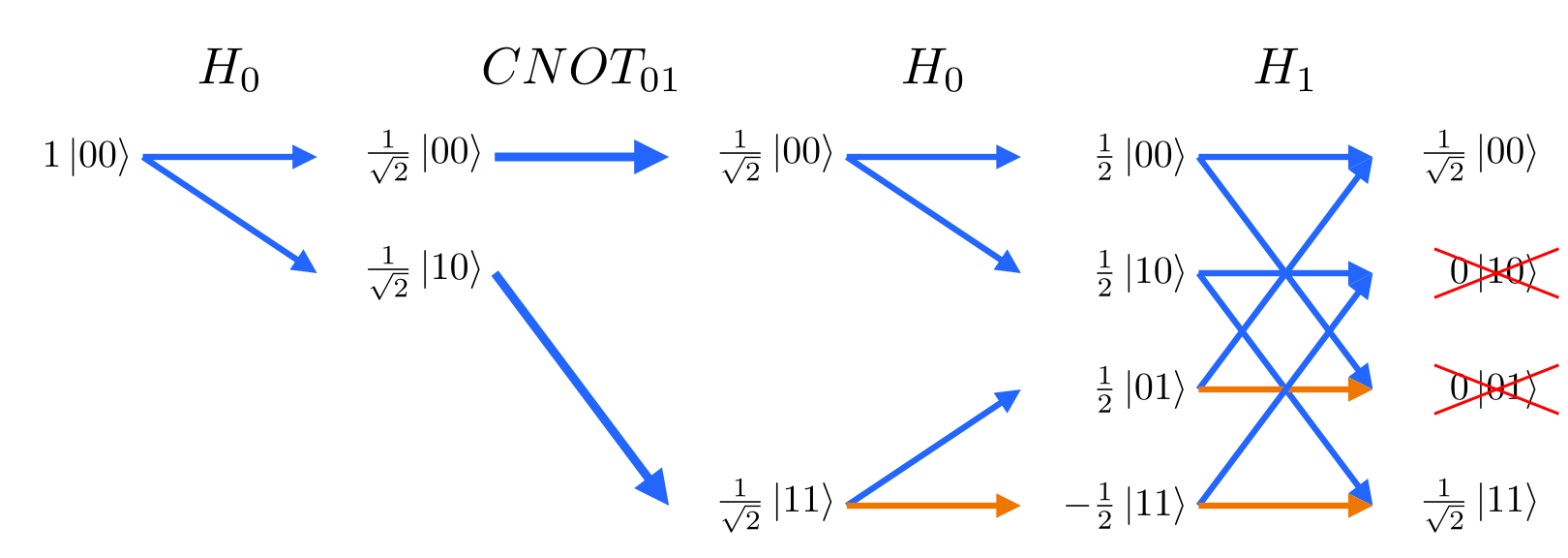
Note the output (rightmost) column is an entangled state: |00⟩+|11⟩
```bash
feynman_path no-entanglement 2 h0 cnot0,1 h0 h1
```
**Fail to create a bell pair by using a CNOT on the |++⟩ state (q0=|+⟩, q1=|+⟩):**


```bash
feynman_path no-entanglement 2 h0 h1 cnot0,1 h0 h1
```
Note the output (rightmost) column is a separable state: |00⟩
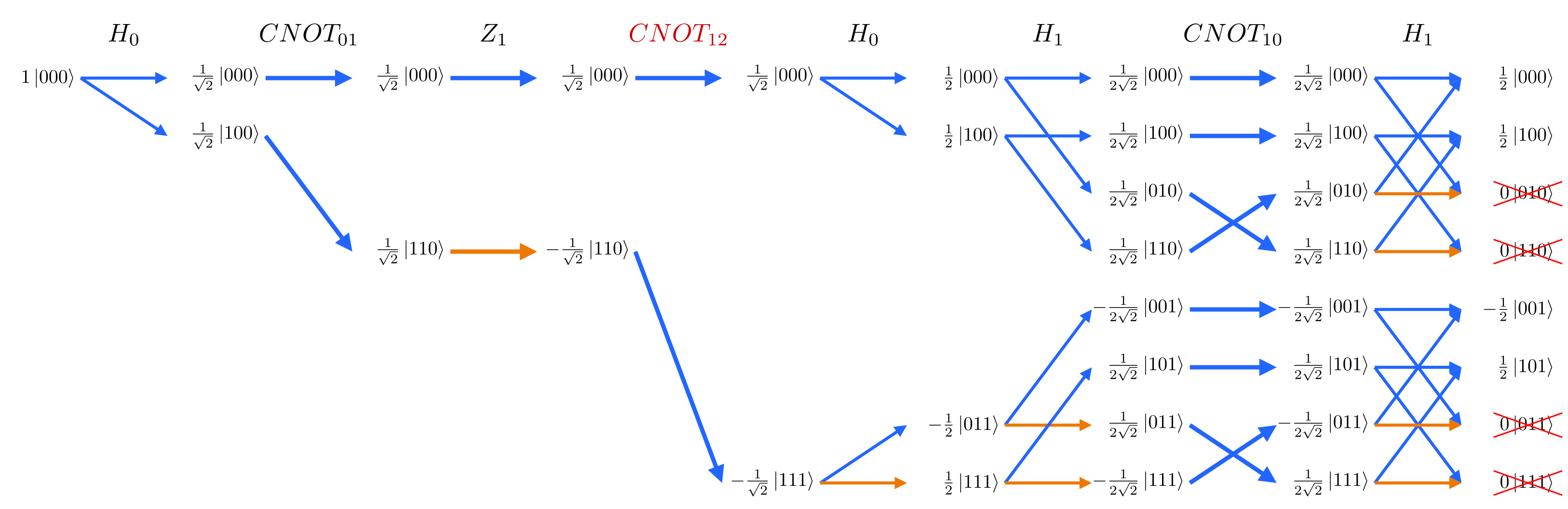
### Copying an intermediate qubit state onto an ancilla ruins interference
In classical computing, it is common to inspect intermediate steps of a computation. This can be very useful for debugging. In quantum computing however, this destroys the effect of interference. We can use a [CNOT gate](https://en.wikipedia.org/wiki/Controlled_NOT_gate) (⋅–⨁) to copy an intermediate value onto another qubit to inspect later. Shown below, copying the intermediate value of q1 to q2 changes the output of q0, q1.
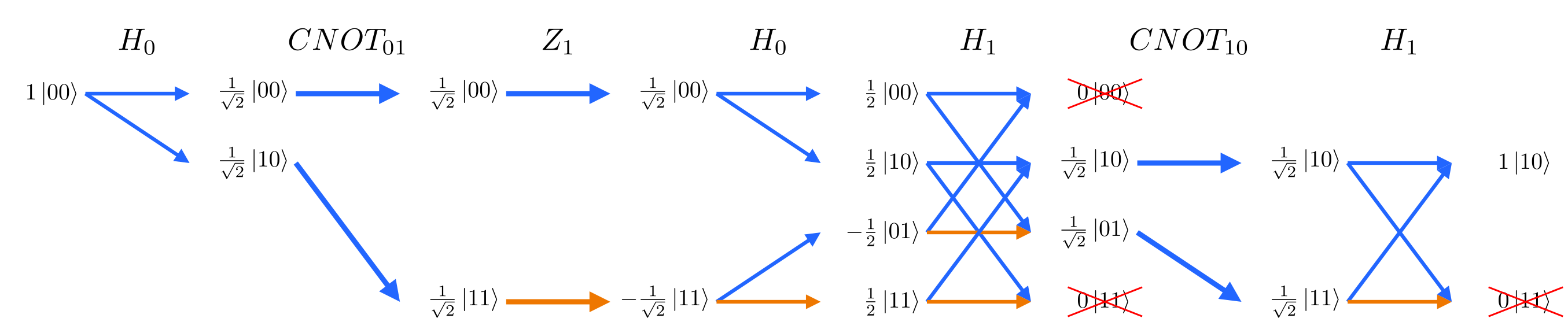
**Original circuit that compute the output q0=1, q1=0:**


```bash
feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1
```
**The addition of CNOT1,2 to inspect the intermediate value of q1 changes the output of q0:**
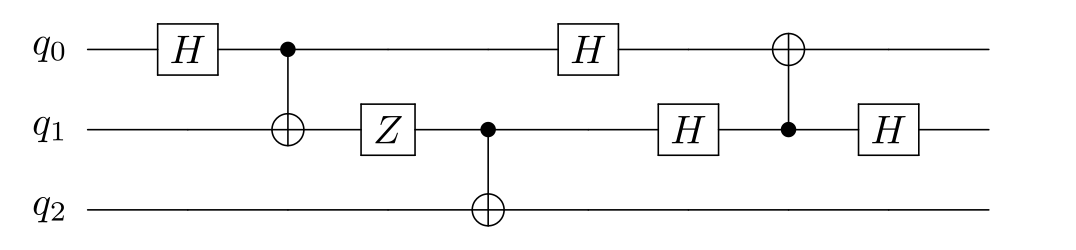

Note how the path diagram is the same except the arrows at H1 are now split into the upper and lower halves of the diagram and don't interfere anymore.
```bash
feynman_path no-interference 3 h0 cnot0,1 z1 cnot1,2 h0 h1 cnot1,0 h1
```