https://github.com/chakravala/dendriform.jl

Dendriform di-algebra algorithms to compute using Loday's arithmetic on groves of planar binary trees
https://github.com/chakravala/dendriform.jl

abstract-algebra binary-trees combinatorics discrete-mathematics graph graph-theory hopf-algebra math mathematics number-theory

Last synced: about 3 hours ago
JSON representation

Dendriform di-algebra algorithms to compute using Loday's arithmetic on groves of planar binary trees

• Host: GitHub
• URL: https://github.com/chakravala/dendriform.jl
• Owner: chakravala
• License: gpl-3.0
• Created: 2017-04-28T20:11:02.000Z (over 7 years ago)
• Default Branch: master
• Last Pushed: 2019-12-07T20:12:22.000Z (almost 5 years ago)
• Last Synced: 2024-05-09T23:42:34.717Z (6 months ago)
• Topics: abstract-algebra, binary-trees, combinatorics, discrete-mathematics, graph, graph-theory, hopf-algebra, math, mathematics, number-theory
• Language: Julia
• Homepage:
• Size: 114 KB
• Stars: 16
• Watchers: 4
• Forks: 5
• Open Issues: 0
• Metadata Files:
  • Readme: README.md
  • License: LICENSE

Awesome Lists containing this project

README

        


  



# Dendriform.jl

*Dendriform dialgebra algorithms to compute using Loday's arithmetic on groves of planar binary trees*

[![Build Status](https://travis-ci.org/chakravala/Dendriform.jl.svg?branch=master)](https://travis-ci.org/chakravala/Dendriform.jl) [![Build status](https://ci.appveyor.com/api/projects/status/j7t3oc1doeot6i72?svg=true)](https://ci.appveyor.com/project/chakravala/grovealg-jl) [![Coverage Status](https://coveralls.io/repos/github/chakravala/Dendriform.jl/badge.svg?branch=master)](https://coveralls.io/github/chakravala/Dendriform.jl?branch=master) [![codecov.io](http://codecov.io/github/chakravala/Dendriform.jl/coverage.svg?branch=master)](http://codecov.io/github/chakravala/Dendriform.jl?branch=master)

[![](https://img.shields.io/badge/docs-stable-blue.svg)](https://chakravala.github.io/Dendriform.jl/stable)

[![](https://img.shields.io/badge/docs-latest-blue.svg)](https://chakravala.github.io/Dendriform.jl/latest)

## Setup

Installation of latest release version using Julia:

```Julia

julia> Pkg.add("Dendriform")

```

Provides the types `PBTree` for planar binary trees, `Grove` for tree collections of constant degree, and `GroveBin` to compress grove data. This package defines various essential operations on planar binary trees and groves like `∪` for `union`; `∨` for `graft`; `left` and `right` for branching; `⋖`, `⋗`, `<`, `>`, `≤`, `≥` for Tamari's partial ordering; `⊴` for `between`; `/` and `\` (i.e. `over` and `under`); and the `dashv` and `vdash` operations `⊣`, `⊢`, `+`, `*` for dendriform algebra.

View the documentation [stable](https://chakravala.github.io/Dendriform.jl/stable) / [latest](https://chakravala.github.io/Dendriform.jl/latest) for more features and examples.

## Background

We call ![tree-symb](https://latex.codecogs.com/svg.latex?\omega(\tau)&space;:=&space;[\omega(\tau^l),n,&space;\omega(\tau^r)]&space;=&space;[d_1,d_2,\dots,d_n]) the *name* of a tree to represent it as a vector, where the sequence is made up of *n* integers.

Collections of planar binary trees are encoded into an equivalence class of matrices:

![matrix-equivalence-class](https://latex.codecogs.com/svg.latex?\mathbb{Y}_n^m&space;\cong&space;\Lambda_n^m&space;=&space;\left\\{A&space;\in&space;\text{Mat}_{m\times&space;n}(\mathbb{Z}^&plus;)&space;:&space;\forall&space;i(\exists!\tau\in\mathbb{Y}_n^1)&space;(A_{i,*}&space;=&space;\omega(\tau)),&space;\forall&space;i,j(A_{i,*}&space;\neq&space;A_{j,*})&space;\right\\}&space;/&space;\sim)

where ![A~B](https://latex.codecogs.com/svg.latex?A&space;\sim&space;B) if there exists a permutation ![f  in Sk](https://latex.codecogs.com/svg.latex?f\in&space;S_k) so that ![condition](https://latex.codecogs.com/svg.latex?\forall&space;i(&space;A_{i,*}&space;=&space;B_{f(i),*})).

The binary tree grafting operation is computed



The left and right addition are computed on the following recursive principle:



Together these non-commutative binary operations satisfy the properties of an associative dendriform dialgebra. The structures induced by Loday's definition of the sum have the partial ordering of the associahedron known as Tamari lattice.



  



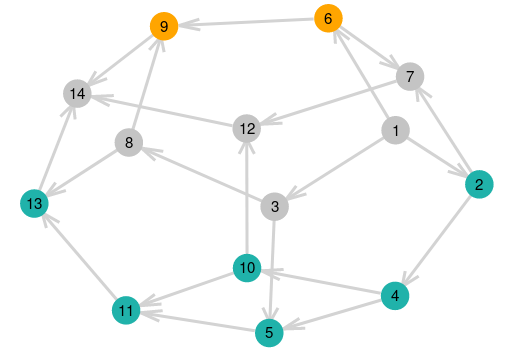
* **Figure**: *Tamari associahedron, colored to visualize noncommutative sums of \[1,2\] and \[2,1\], code: [gist](https://gist.github.com/chakravala/fbc1b1a34adaeb7fdac93b3d488c57a4)*

However, in this computational package, a stricter total ordering is constructed using a function that transforms the set-vector isomorphism obtained from the descending greatest integer index position search method:



The structure obtained from this total ordering is used to construct a reliable binary `groveindex` representation that encodes the essential data of any grove, using the formula



These algorithms are used in order to facilitate computations that provide insight into the Loday arithmetic.

## Usage

Basic usage examples:

```Julia

julia> using Dendriform

julia> Grove(3,7) ⊣ [1,2]∪[2,1]

[1,2,5,1,2]

[1,2,5,2,1]

[2,1,5,1,2]

[2,1,5,2,1]

[1,5,3,1,2]

[1,5,2,1,3]

[1,5,1,2,3]

[1,5,3,2,1]

[1,5,1,3,1]

Y5 #9/42

julia> Grove(2,3) * ([1,2,3]∪[3,2,1]) |> GroveBin

2981131286847743360614880957207748817969 Y6 #30/132 [54.75%]

julia> [2,1,7,4,1,3,1] < [2,1,7,4,3,2,1]

true

```

## References

* Dan Yasaki with Adriano Bruno, [The arithmetic of planar binary trees](http://libres.uncg.edu/ir/uncg/f/D_Yasaki_Arithmetic_2011.pdf), Involve 4 (2011), no. 1, 1-11. ([PDF](https://www.uncg.edu/mat/faculty/d_yasaki/publications/trees_for_print.pdf))

* Jean-Louis Loday, [Arithmetree](http://irma.math.unistra.fr/~loday/PAPERS/2002Loday(arithmetree).pdf), J. of Algebra (2002), no. 258, 275-309.