Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/crowsonkb/mdmm

The Modified Differential Multiplier Method (MDMM) for PyTorch
https://github.com/crowsonkb/mdmm

constrained-optimization optimization pytorch

Last synced: about 1 month ago
JSON representation

The Modified Differential Multiplier Method (MDMM) for PyTorch

Awesome Lists containing this project

README 

        
# mdmm



`mdmm` implements the Modified Differential Multiplier Method for PyTorch. It was proposed in Platt and Barr (1988), "[Constrained Differential Optimization](https://papers.nips.cc/paper/1987/file/a87ff679a2f3e71d9181a67b7542122c-Paper.pdf)". The MDMM minimizes a primary loss function subject to equality, inequality, and bound constraints on arbitrarily many secondary functions of your problem's parameters. It can be used for non-convex problems and problems with stochastic loss functions. It requires only one evaluation of the Lagrangian and its gradient per iteration, the same complexity as SGD.



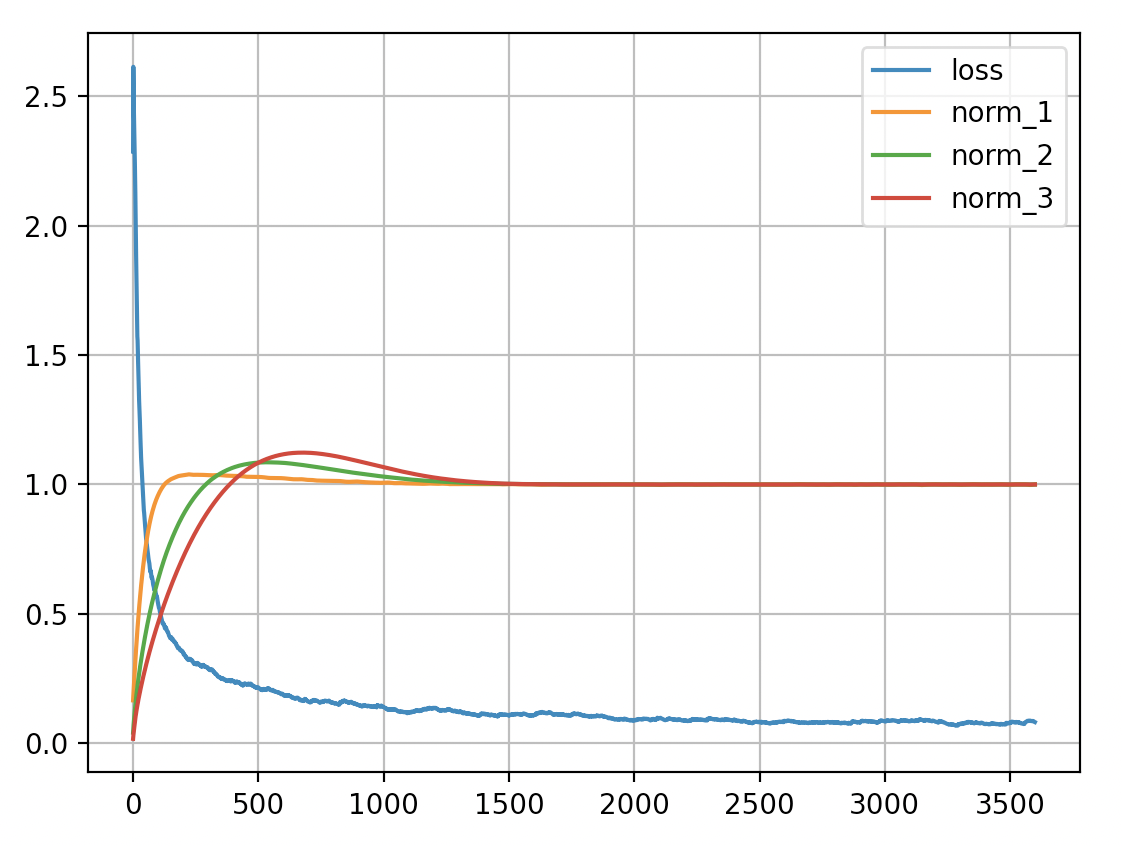
Here is a plot of the training loss and layer norms of `mdmm_demo_mnist.py`. Each of its three layers has an equality constraint that the mean absolute value of its weights be 1:






## Installation



`mdmm` is [on PyPI](https://pypi.org/project/mdmm/) and can be installed with:



```sh

pip install mdmm

```



## Basic usage



Creating a constraint instance, an `MDMM` instance, and the optimizer for the Lagrangian:



```python

import mdmm



constraint = mdmm.EqConstraint(fn_of_params, 1)

mdmm_module = mdmm.MDMM([constraint])

opt = mdmm_module.make_optimizer(model.parameters(), lr=2e-3)

```



The first argument to the constraint constructor should be a differentiable function that takes no arguments and returns a zero-dimensional PyTorch `Tensor` (a single value).



MDMM constraints introduce extra parameters (Lagrange multipliers and slack variables) which must be included in the optimizer. Each `MaxConstraint` and `MinConstraint` introduces two parameters each, while all of the other constraint types introduce one. `make_optimizer()` accepts an optional optimizer factory keyword argument, `optimizer`, which can be set to a `torch.optim` class; use `functools.partial()` on the class to set the optimizer's arguments to non-default values. The default optimizer type is Adamax.



Inside your training loop, do:



```python

outputs = model(inputs)

loss = loss_fn(outputs, targets)

mdmm_return = mdmm_module(loss)

opt.zero_grad()

mdmm_return.value.backward()

opt.step()

```



When an `MDMM` instance is called with the value of the primary loss function, it evaluates the functions originally passed to the constraints' constructors and returns a type containing a value augmented with terms involving the constraint functions. Calling `backward()` on this value will propagate gradients into your parameters and the parameters internal to the constraints. The type `MDMM` returns also contains a list of the constraint function values and a list of the computed infeasibilities (equal to 0 when the constraint is satisfied).



Since the constraints contain parameters internal to them, you must save and load the state dict of the `MDMM` instance (this contains all of the constraint buffers and parameters in the correct order) as well as the model and optimizer state dicts in order to be able to resume training from a checkpoint.



## Constraint details



There are six supported constraint types:



* `EqConstraint(fn, value)` represents an equality constraint on `fn`.



* `MaxConstraint(fn, max)` represents a maximum inequality constraint on `fn` which uses a slack variable.



* `MaxConstraintHard(fn, max)` represents a maximum inequality constraint on `fn` without a slack variable.



* `MinConstraint(fn, min)` represents a minimum inequality constraint on `fn` which uses a slack variable.



* `MinConstraintHard(fn, min)` represents a minimum inequality constraint on `fn` without a slack variable.



* `BoundConstraintHard(fn, min, max)` represents a bound constraint on `fn`. It does not use slack variables.



All MDMM constraints take a scale factor (`scale`) and a damping strength (`damping`) as optional arguments. The scale factor allows you to scale the computed infeasibility relative to the primary loss function's value. It may be needed if the magnitude of the primary loss function is very large or small compared to the constraint functions' magnitudes. The MDMM augments the Lagrangian with quadratic damping terms that help reduce oscillations in the infeasibilities. The damping strength can be manually decreased if there are no oscillations observed and increased if there are oscillations. The defaults for `scale` and `damping` are both 1.



## A warning about lambda expressions



The following code is incorrect:



```python

constraints = []

for layer in model:

    if hasattr(layer, 'weight'):

        constraints.append(mdmm.EqConstraint(lambda: layer.weight.abs.mean(), 1))

```



`layer` is a free variable inside the lambda expression and will be resolved at call time to the *current* value of `layer` in the enclosing code block, which is updated by the loop, so all of the constraints will refer to the last layer! A correct version is:



```python

from functools import partial



constraints = []

for layer in model:

    if hasattr(layer, 'weight'):

        fn = partial(lambda x: x.weight.abs().mean(), layer)

        constraints.append(mdmm.EqConstraint(fn, 1))

```



`partial()` captures the value of the `layer` argument inside the callable it returns, so `fn` acts on the layer it was created with.