Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/cyrildever/treee

Fast indexing engine for data identified by hashed id and stored in an immutable file
https://github.com/cyrildever/treee

file golang hash http-server immutable microservice search-engine

Last synced: 2 months ago
JSON representation

Fast indexing engine for data identified by hashed id and stored in an immutable file

Awesome Lists containing this project

README 

        
# treee

_Fast indexing engine for data identified by hashed id and stored in an immutable file_



![GitHub tag (latest by date)](https://img.shields.io/github/v/tag/cyrildever/treee)

![GitHub last commit](https://img.shields.io/github/last-commit/cyrildever/treee)

![GitHub issues](https://img.shields.io/github/issues/cyrildever/treee)

![GitHub](https://img.shields.io/github/license/cyrildever/treee)



This is the Go implementation of the Treee™ indexing engine.

It's both a [library](#usage) to use as a module in your Go projects and an [executable](#executable) to run as a micro-service over HTTP.



### Motivation



The challenge was to set up a powerful and safe search engine to use when the data is some linked list of items that could be themselves connected to each other in subchains, indexed through their identifiers that are only made of hashed values (like SHA-256 string representations), and all stored in an immutable file.



Its best application is for a Blockchain file where an item is a transaction embedding a smart contract, and each subchain of items the subsequent uses and/or modifications of this smart contract.

As such, the Treee™ index is currently used in the [Rooot™](https://rooot.io) blockchain.



### Formal description



We define here an algorithm for indexing the system based on identifiers that are hashed values which is at the same time very powerful to the writing and the reading.



#### 1) How the index works



The Treee™ index is constructed as an acyclic graph (a tree). Each node contains either the node address (its sons) or a set of *Leafs*, a *Leaf* corresponding to the information helping to retrieve one or more linked items.



The number of sons of a node is deterministic and depends on the depth of the tree. We denote by 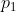 the number of sons of the nodes at depth 1,  the number of sons of the nodes at depth 2, ...,  the number of sons at depth .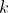



The goal is to create a balanced tree whose width is adaptive to decrease depth and optimize performance. We are looking to index numbers, in this case the numerical value of the items' unique identifiers.



Let's explain the course of the index.



For the binary tree, we write the number in binary form (for example,  `100`) which indicates its position in the tree.



At the step 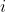, we pass to the child  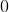if the  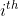bit is `0`, otherwise we pass to the child  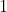if the  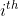bit is `1`. We stop when the node is a *Leaf*.



For the tree, we build a representation of this number by a sequence of numbers and we traverse the tree in the same way. At the step 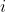 of depth 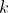, we pass to the child  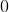if the  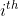representative is `0`, we pass to the child  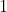if the  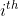representative is `1`, ..., we pass to the child  if the 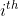 representative is . We stop when the node is a *Leaf*.



To construct the representation of a number, we will successively take the modulo of prime numbers. According to the theorem of the Chinese remains, each number has a unique representative that could be written as the continuation of these modulos. Indeed, a number 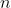 can be written in the following form: 



The value of the identifier of the item (its number) is denoted 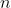 and the modulating number 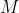. Modulos are calculated in  for fixed-sized integers. Since the multiplication is faster than the division (necessary for the calculation of the modulo), one can use multiplications by means of floating: .



Given the random nature of the numbers (or pseudo-random, since the identifiers of the items are generated by cryptographic hashing technologies), the tree is balanced. To unbalance the tree in a malicious way, it would be necessary to be able to generate hashes whose modulo follows a particular trajectory. 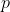However, the difficulty of such an operation increases exponentially (of the order of  where  is the depth).

As a reminder, the product of the first 16 prime numbers equals .

Therefore, as soon as the index contains a reasonably large amount of data, unbalancing the tree in a malicious way would become more and more impossible, if at all possible.



A *Leaf* contains the following list of information about an item:

 * Identifier of the current item as a hash string;

 * Position: start address of the current item in the file;

 * Size: the size (in bytes) of the saved item in the file;

 * Origin: unique identifier of the item that is at the origin of the item's subchain;

 * Previous: unique identifier of the previous item chained to it;

 * Next: optionally, unique identifier of the next item chained.



 A *Leaf* whose next item field is empty is the last item in the subchain.

 

 A *Leaf* whose origin item field is equal to the identifier of the current item is necessarily the origin of the subchain. As such, it has a particular operating since, if there were to be one or more items thereafter, the last item of the subchain will be identified here as the previous item. The last three fields of the *Leaf* therefore correspond to a circular linked list.



#### 2) Using the index



To add an element to the index:

* The new *Leaf* is written in the index;

* We update the 'Next' field of the *Leaf* that previously corresponded to the last item of the subchain;

* We modify the 'Previous' field of the *Leaf* of the original item by writing the identifier of the current item.



To read/search an item in the index:

* We find in the tree the *Leaf* corresponding to the identifier of the searched item:

  * If the 'Next' field of the *Leaf* is empty, this is the last item of the subchain;

  * Otherwise, we go to the next step;

* We find the *Leaf* corresponding to the identifier of the field 'Origin';

* We use the 'Previous' field of this *Leaf* to find the last item of the subchain.



When using the index, we can seen that we would perform at most 3 reads or 3 writes and index runs of  order, where 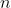 is the number of items in the index.



For more details, feel free to read the full [white paper](documentation/src/latex/treee_whitepaper.pdf).



### Usage



```console

$ go get github.com/cyrildever/treee

```



```golang

import (

  "github.com/cyrildever/treee/core/index"

  "github.com/cyrildever/treee/core/index/branch"

  "github.com/cyrildever/treee/core/model"

)



// Instantiate default index (could be any prime number up to the 1000th existing prime number,

// but should be much lower to better leverage the solution, and if 0 will use the default INIT_PRIME value)

treee, err := index.New(index.INIT_PRIME)

if err != nil {

  // Handle error

}



// Add to index

leaf := branch.Leaf{

  ID: model.Hash("1234567890abcdef"),

  Position: 0,

  Size: 100,

}

err = treee.Add(leaf)

if err != nil {

  // Handle error

}



// Search

if found, err := treee.Search(leaf.ID); err == nil {

  // Do something with found Leaf

}

```



For better performance, you should put your search requests in different goroutines (see `GetLeaf()` implementation in [api/handlers/leaf.go](api/handlers/leaf.go) file for example).



For debugging or storage purposes, you might want to use the `PrintAll()` method on the `Treee` index to print all recorded leaves to a writer (passing it `true` as argument for beautifying the printed JSON, or `false` for the raw string).

```golang

// To print to Stdout

fmt.Println(treee.PrintAll(true))

```



Persistence of the index is achieved through the use of the automatic save made upon insertion, and the use of the `Load()` function instead of Treee instantiation with `New()` at start-up.

```golang

treee, err := index.Load("path/to/treee.json") // If empty, will use "./saved/treee.json"

```

It could be disabled using the corresponding environment variable or flag in the command line, or even programmatically:

```golang

treee.UsePersistence(false) // If you're positive you don't want it

```



### Executable



You can simply build the executable and start an instance of the Treee™ indexing engine.



```console

$ git clone https://github.com/cyrildever/treee.git && cd treee && go build

$ ./treee -t.port 7001 -t.host localhost -t.init 101

```



```

Usage of ./treee:

  -t.file string

        File path to an existing index

  -t.host string

        Host address (default "0.0.0.0")

  -t.init string

        Initial prime number to use for the index (default "0")

  -t.persist

        Activate persistence (default true)

  -t.port string

        HTTP port number (default "7000")

```



##### Environment variables



If set, the following environment variables will override any corresponding default configuration or flag passed with the command line:

- `HOST`: the host address;

- `HTTP_PORT`: the HTTP port number to use;

- `INDEX_PATH`: the path to the index file in JSON format;

- `INIT_PRIME`: the initial prime number (note that it won't have any effect if using a file because the latter will prevail);

- `USE_PERSISTENCE`: set `false` to disable the use of saving the index into a file.



##### API



The following endpoints are available under the `/api` group:



* `DELETE /leaf`



This endpoint removes the passed items from the index.



It expects an array of IDs as `ids` query argument, eg.

```http

DELETE /api/leaf?ids=1235467890abcdef[...]&ids=fedcba0987654321[...]

User-Agent: Mozilla/4.0 (compatible; MSIE5.01; Windows NT)

Host: treee.io

Accept-Language: fr-FR

Accept-Encoding: gzip, deflate

Accept: application/json

```



It returns a `204` status code if all passed items were removed, or a `200` status code along with the following json list of undeleted IDs if some weren't removed:

```json

{

  "ids": ["fedcba0987654321[...]"]

}

```



* `GET /leaf`



This endpoint searches items based on the passed IDs.



It expects an array of IDs as `ids` query argument and an optional `takeLast` boolean (default to `false`), eg. `http://localhost:7000/api/leaf?ids=1234567890abcdef[...]&ids=fedcba0987654321[...]&takeLast=true`



It returns a status code `200` along with a JSON object respecting the following format:

```json

[

  {

    "id": "1234567890abcdef[...]",

    "position": 0,

    "size": 100,

    "origin": "1234567890abcdef[...]",

    "previous": "1234567890abcdef[...]",

    "next": ""

  },

  [...]

]

```



In case no item were found, it returns a `404` status code with an empty body.



* `GET /line`



This endpoint returns all the IDs in the same subchain/line.



It expects any ID of a line as `id` query argument, eg. `http://localhost:7000/api/line?id=1234567890abcdef[...]`



It returns a status code `200` long with the following JSON sorted array of IDs (index `0` being the origin):

```json

[

  "1234567890abcdef[...]",

  "fedcba0987654321[...]"

]

```



In case no item were found, it returns a `404` status code with an empty body.



* `POST /leaf`



This endpoint adds an item to the index.



It expects the following JSON object as body, the first three fields being mandatory:

```json

{

  "id": "",

  "position": 0,

  "size": 100,

  "previous": ""

}

```



It returns a status code and the following object as JSON:

```json

{

  "code": 200 | 303 | 400 | 404 | 412 | 500,

  "result": "",

  "error": ""

}

```



The list of status codes (and their meaning) is as follows:

  - `200`: item inserted;

  - `303`: item already exists (not updated as the file is supposed to be immutable);

  - `400`: wrong parameter (missing item, missing mandatory field, etc.);

  - `404`: passed previous item not found;

  - `412`: something in the passed data caused the server to fail (incorrect JSON format, ...);

  - `500`: an error occurred on the server.



### Performances



In average, a basic machine should be able to ingest over 100 millions new records and handle about 5 billions search queries per hour.



As an example, on an Apple MacBook Pro 2.3 GHz Intel Core i9 with 16 Go DDR4 RAM clocked at 2400 MHz, I observed the following performances when using `101` as init prime:

- insertion: 10,000 additions in ~300ms (120 millions per hour);

- search: 1,000,000 requests in ~500ms, ie. approx. 2 MHz (over 7 billions per hour).

And on an Apple iMac 3.1 Ghz Intel Core i5 with 16 Go DDR4 RAM clocked at 2667 MHz also using `101` as init prime:

- insertion: 10,000 additions in ~240ms (150 millions per hour);

- search: 1,000,000 requests in ~750ms, ie. approx. 1.3 MHz (over 4.8 billions per hour).



### License



This module is distributed under a MIT license. \

See the [LICENSE](LICENSE) file.





© 2018-2024 Cyril Dever. All rights reserved.