https://github.com/d-krupke/cpsat-primer
The CP-SAT Primer: Using and Understanding Google OR-Tools' CP-SAT Solver
https://github.com/d-krupke/cpsat-primer
combinatorial-optimization cp-sat operations-research optimization ortools
Last synced: 7 months ago
JSON representation
The CP-SAT Primer: Using and Understanding Google OR-Tools' CP-SAT Solver
- Host: GitHub
- URL: https://github.com/d-krupke/cpsat-primer
- Owner: d-krupke
- License: cc-by-4.0
- Created: 2022-07-10T08:00:40.000Z (over 3 years ago)
- Default Branch: main
- Last Pushed: 2024-10-24T19:01:13.000Z (about 1 year ago)
- Last Synced: 2024-10-30T03:42:41.468Z (about 1 year ago)
- Topics: combinatorial-optimization, cp-sat, operations-research, optimization, ortools
- Language: Jupyter Notebook
- Homepage: https://d-krupke.github.io/cpsat-primer/
- Size: 21.2 MB
- Stars: 367
- Watchers: 14
- Forks: 35
- Open Issues: 7
-
Metadata Files:
- Readme: README.md
- Contributing: CONTRIBUTING.md
- License: LICENSE
- Citation: CITATION.cff
Awesome Lists containing this project
- awesome_or-tools - CP-SAT Primer
README
*A book-style version of this primer is available at [https://d-krupke.github.io/cpsat-primer/](https://d-krupke.github.io/cpsat-primer/).*
# The CP-SAT Primer: Using and Understanding Google OR-Tools' CP-SAT Solver
_By [Dominik Krupke](https://krupke.cc), TU Braunschweig, with contributions
from Leon Lan, Michael Perk, and
[others](https://github.com/d-krupke/cpsat-primer/graphs/contributors)._
Many [combinatorially difficult](https://en.wikipedia.org/wiki/NP-hardness)
optimization problems can, despite their proven theoretical hardness, be solved
reasonably well in practice. The most successful approach is to use
[Mixed Integer Linear Programming](https://en.wikipedia.org/wiki/Integer_programming)
(MIP) to model the problem and then use a solver to find a solution. The most
successful solvers for MIPs are, e.g., [Gurobi](https://www.gurobi.com/),
[CPLEX](https://www.ibm.com/analytics/cplex-optimizer),
[COPT Cardinal Solver](https://www.copt.de/), and
[FICO Xpress Optimization](https://www.fico.com/en/products/fico-xpress-optimization),
which are all commercial and expensive (though, mostly free for academics).
There are also some open source solvers (e.g., [SCIP](https://www.scipopt.org/)
and [HiGHS](https://highs.dev/)), but they are often not as powerful as the
commercial ones (yet). However, even when investing in such a solver, the
underlying techniques
([Branch and Bound](https://en.wikipedia.org/wiki/Branch_and_bound) &
[Cut](https://en.wikipedia.org/wiki/Branch_and_cut) on
[Linear Relaxations](https://en.wikipedia.org/wiki/Linear_programming_relaxation))
struggle with some optimization problems, especially if the problem contains a
lot of logical constraints that a solution has to satisfy. In this case, the
[Constraint Programming](https://en.wikipedia.org/wiki/Constraint_programming)
(CP) approach may be more successful. For Constraint Programming, there are many
open source solvers, but they usually do not scale as well as MIP-solvers and
are worse in optimizing objective functions. While MIP-solvers are frequently
able to optimize problems with hundreds of thousands of variables and
constraints, the classical CP-solvers often struggle with problems with more
than a few thousand variables and constraints. However, the relatively new
[CP-SAT](https://developers.google.com/optimization/cp/cp_solver) of Google's
[OR-Tools](https://github.com/google/or-tools/) suite shows to overcome many of
the weaknesses and provides a viable alternative to MIP-solvers, being
competitive for many problems and sometimes even superior.
As a quick demonstration of CP-SAT's capabilities - particularly for those less
familiar with optimization frameworks - let us solve an instance of the NP-hard
Knapsack Problem. This classic optimization problem requires selecting a subset
of items, each with a specific weight and value, to maximize the total value
without exceeding a weight limit. Although a recursive algorithm is easy to
implement, 100 items yield approximately $2^{100} \approx 10^{30}$ possible
solutions. Even with a supercomputer performing $10^{18}$ operations per second,
it would take more than 31,000 years to evaluate all possibilities.
Here is how you can solve it using CP-SAT:
```python
from ortools.sat.python import cp_model # pip install -U ortools
# Specifying the input
weights = [395, 658, 113, 185, 336, 494, 294, 295, 256, 530, 311, 321, 602, 855, 209, 647, 520, 387, 743, 26, 54, 420, 667, 971, 171, 354, 962, 454, 589, 131, 342, 449, 648, 14, 201, 150, 602, 831, 941, 747, 444, 982, 732, 350, 683, 279, 667, 400, 441, 786, 309, 887, 189, 119, 209, 532, 461, 420, 14, 788, 691, 510, 961, 528, 538, 476, 49, 404, 761, 435, 729, 245, 204, 401, 347, 674, 75, 40, 882, 520, 692, 104, 512, 97, 713, 779, 224, 357, 193, 431, 442, 816, 920, 28, 143, 388, 23, 374, 905, 942]
values = [71, 15, 100, 37, 77, 28, 71, 30, 40, 22, 28, 39, 43, 61, 57, 100, 28, 47, 32, 66, 79, 70, 86, 86, 22, 57, 29, 38, 83, 73, 91, 54, 61, 63, 45, 30, 51, 5, 83, 18, 72, 89, 27, 66, 43, 64, 22, 23, 22, 72, 10, 29, 59, 45, 65, 38, 22, 68, 23, 13, 45, 34, 63, 34, 38, 30, 82, 33, 64, 100, 26, 50, 66, 40, 85, 71, 54, 25, 100, 74, 96, 62, 58, 21, 35, 36, 91, 7, 19, 32, 77, 70, 23, 43, 78, 98, 30, 12, 76, 38]
capacity = 2000
# Now we solve the problem
model = cp_model.CpModel()
xs = [model.new_bool_var(f"x_{i}") for i in range(len(weights))]
model.add(sum(x * w for x, w in zip(xs, weights)) <= capacity)
model.maximize(sum(x * v for x, v in zip(xs, values)))
solver = cp_model.CpSolver()
solver.solve(model)
print("Optimal selection:", [i for i, x in enumerate(xs) if solver.value(x)])
print("Total packed value:", solver.objective_value)
```
```
Optimal selection: [2, 14, 19, 20, 29, 33, 52, 53, 54, 58, 66, 72, 76, 77, 81, 86, 93, 94, 96]
Total packed value: 1161.0
```
How long did CP-SAT take? On my machine, it found the provably best solution
from $2^{100}$ possibilities in just 0.01 seconds. Feel free to try it on yours.
CP-SAT does not evaluate all solutions; it uses advanced techniques to make
deductions and prune the search space. While more efficient approaches than a
naive recursive algorithm exist, matching CP-SAT’s performance would require
significant time and effort. And this is just the beginning - CP-SAT can tackle
much more complex problems, as we will see in this primer.
> [!TIP]
>
> Not convinced yet of why tools like CP-SAT are amazing? Maybe Marco Lübbecke
> can convince you in his 12-minute TEDx talk
> [Anything you can do I can do better](https://www.youtube.com/watch?v=Dc38La-Xvog)
> about mathematical optimization.
### Content
Whether you are from the MIP community seeking alternatives or CP-SAT is your
first optimization solver, this book will guide you through the fundamentals of
CP-SAT in the first part, demonstrating all its features. The second part will
equip you with the skills needed to build and deploy optimization algorithms
using CP-SAT.
The first part introduces the fundamentals of CP-SAT, starting with a chapter on
installation. This chapter guides you through setting up CP-SAT and outlines the
necessary hardware requirements. The next chapter provides a simple example of
using CP-SAT, explaining the mathematical notation and its approximation in
Python with overloaded operators. You will then progress to basic modeling,
learning how to create variables, objectives, and fundamental constraints in
CP-SAT.
Following this, a chapter on advanced modeling will teach you how to handle
complex constraints, such as circuit constraints and intervals, with practical
examples. Another chapter discusses specifying CP-SAT's behavior, including
setting time limits and using parallelization. You will also find a chapter on
interpreting CP-SAT logs, which helps you understand how well CP-SAT is managing
your problem. Additionally, there is an overview of the underlying techniques
used in CP-SAT. The first part concludes with a chapter comparing CP-SAT with
other optimization techniques and tools, providing a broader context.
The second part delves into more advanced topics, focusing on general skills
like coding patterns and benchmarking rather than specific CP-SAT features. A
chapter on coding patterns offers basic design patterns for creating
maintainable algorithms with CP-SAT. Another chapter explains how to provide
your optimization algorithm as a service by building an optimization API. There
is also a chapter on developing powerful heuristics using CP-SAT for
particularly difficult or large problems. The second part concludes with a
chapter on benchmarking, offering guidance on how to scientifically benchmark
your model and interpret the results.
### Target Audience
I wrote this book for my computer science students at TU Braunschweig, and it is
used as supplementary material in my algorithm engineering courses. Initially,
we focused on Mixed Integer Programming (MIP), with CP-SAT discussed as an
alternative. However, we recently began using CP-SAT as the first optimization
solver due to its high-level interface, which is much easier for beginners to
grasp. Despite this shift, because MIP is more commonly used, the book includes
numerous comparisons to MIP. Thus, it is designed to be beginner-friendly while
also addressing the needs of MIP users seeking alternatives.
Unlike other books aimed at mathematical optimization or operations research
students, this one, aimed at computer science students, emphasizes coding over
mathematics or business cases, providing a hands-on approach to learning
optimization. The second part of the book can also be interesting for more
advanced users, providing content that I found missing in other books on
optimization.
### Table of Content
**Part 1: The Basics**
1. [Installation](#01-installation): Quick installation guide.
2. [Example](#02-example): A short example, showing the usage of CP-SAT.
3. [Basic Modeling](#04-modelling): An overview of variables, objectives, and
constraints.
4. [Advanced Modeling](#04B-advanced-modelling): More complex constraints, such
as circuit constraints and intervals.
5. [Parameters](#05-parameters): How to specify CP-SATs behavior, if needed.
Timelimits, hints, assumptions, parallelization, ...
6. [Understanding the Log](#understanding-the-log): How to interpret the log
7. [How does it work?](#07-under-the-hood): After we know what we can do with
CP-SAT, we look into how CP-SAT will do all these things.
8. [Alternatives](#03-big-picture): An overview of the different optimization
techniques and tools available. Putting CP-SAT into context.
**Part 2: Advanced Topics**
7. [Coding Patterns](#06-coding-patterns): Basic design patterns for creating
maintainable algorithms.
8. [(DRAFT) Building an Optimization API](#building_an_optimization_api) How to
build a scalable API for long running optimization jobs.
9. [(DRAFT) CP-SAT vs. ML vs. QC](#chapters-machine-learning): A comparison of
CP-SAT with Machine Learning and Quantum Computing.
10. [Large Neighborhood Search](#09-lns): The use of CP-SAT to create more
powerful heuristics.
11. [Benchmarking your Model](#08-benchmarking): How to benchmark your model and
how to interpret the results.
### Background
This book assumes you are fluent in Python, and have already been introduced to
combinatorial optimization problems. In case you are just getting into
combinatorial optimization and are learning on your own, I recommend starting
with the free Coursera course,
[Discrete Optimization](https://www.coursera.org/learn/discrete-optimization),
taught by Pascal Van Hentenryck and Carleton Coffrin. This course provides a
comprehensive introduction in a concise format.
For an engaging exploration of a classic problem within this domain,
[In Pursuit of the Traveling Salesman by Bill Cook](https://press.princeton.edu/books/paperback/9780691163529/in-pursuit-of-the-traveling-salesman)
is highly recommended. This book, along with this
[YouTube talk](https://www.youtube.com/watch?v=5VjphFYQKj8) by the author that
lasts about an hour, offers a practical case study of the well-known Traveling
Salesman Problem. It not only introduces fundamental techniques but also delves
into the community and historical context of the field.
Additionally, the article
[Mathematical Programming](https://www.gurobi.com/resources/math-programming-modeling-basics/)
by CP-SAT's competitor Gurobi offers an insightful introduction to mathematical
programming and modeling. In this context, the term "Programming" does not refer
to coding; rather, it originates from an earlier usage of the word "program",
which denoted a plan of action or a schedule. If this distinction is new to you,
it is a strong indication that you would benefit from reading this article.
> **About the Lead Author:** [Dr. Dominik Krupke](https://krupke.cc) is a
> postdoctoral researcher with the
> [Algorithms Division](https://www.ibr.cs.tu-bs.de/alg) at TU Braunschweig. He
> specializes in practical solutions to NP-hard problems. Initially focused on
> theoretical computer science, he now applies his expertise to solve what was
> once deemed impossible, frequently with the help of CP-SAT. This primer on
> CP-SAT, first developed as course material for his students, has been extended
> in his spare time to cater to a wider audience.
>
> **Contributors:** This primer has been enriched by the contributions of
> [several individuals](https://github.com/d-krupke/cpsat-primer/graphs/contributors).
> Notably, Leon Lan played a key role in restructuring the content and offering
> critical feedback, while Michael Perk significantly enhanced the section on
> the reservoir constraint. I also extend my gratitude to all other contributors
> who identified and corrected errors, improved the text, and offered valuable
> insights.
> **Found a mistake?** Please open an issue or a pull request. You can also just
> write me a quick mail to `krupked@gmail.com`.
> **Want to contribute?** If you are interested in contributing, please open an
> issue or email me with a brief description of your proposal. We can then
> discuss the details. I welcome all assistance and am open to expanding the
> content. Contributors to any section or similar input will be recognized as
> coauthors.
> **Want to use/share this content?** This tutorial can be freely used under
> [CC-BY 4.0](https://creativecommons.org/licenses/by/4.0/). Smaller parts can
> even be copied without any acknowledgement for non-commercial, educational
> purposes.
---
# Part 1: The Basics
## Installation
We are using Python 3 in this primer and assume that you have a working Python 3
installation as well as the basic knowledge to use it. There are also interfaces
for other languages, but Python 3 is, in my opinion, the most convenient one, as
the mathematical expressions in Python are very close to the mathematical
notation (allowing you to spot mathematical errors much faster). Only for huge
models, you may need to use a compiled language such as C++ due to performance
issues. For smaller models, you will not notice any performance difference.
The installation of CP-SAT, which is part of the OR-Tools package, is very easy
and can be done via Python's package manager
[pip](https://pip.pypa.io/en/stable/).
```shell
pip3 install -U ortools
```
This command will also update an existing installation of OR-Tools. As this tool
is in active development, it is recommended to update it frequently. We actually
encountered wrong behavior, i.e., bugs, in earlier versions that then have been
fixed by updates (this was on some more advanced features, do not worry about
correctness with basic usage).
I personally like to use [Jupyter Notebooks](https://jupyter.org/) for
experimenting with CP-SAT.
### What hardware do you need?
It is important to note that for CP-SAT usage, you do not need the capabilities
of a supercomputer. A standard laptop is often sufficient for solving many
problems. The primary requirements are CPU power and memory bandwidth, with a
GPU being unnecessary.
In terms of CPU power, the key is balancing the number of cores with the
performance of each individual core. CP-SAT leverages all available cores by
default, implementing different strategies on each.
[Depending on the number of cores, CP-SAT will behave differently](https://github.com/google/or-tools/blob/main/ortools/sat/docs/troubleshooting.md#improving-performance-with-multiple-workers).
However, the effectiveness of these strategies can vary, and it is usually not
apparent which one will be most effective. A higher single-core performance
means that your primary strategy will operate more swiftly. I recommend a
minimum of 4 cores and 16GB of RAM.
While CP-SAT is quite efficient in terms of memory usage, the amount of
available memory can still be a limiting factor in the size of problems you can
tackle. When it came to setting up our lab for extensive benchmarking at TU
Braunschweig, we faced a choice between desktop machines and more expensive
workstations or servers. We chose desktop machines equipped with AMD Ryzen 9
7900 CPUs (Intel would be equally suitable) and 96GB of DDR5 RAM, managed using
Slurm. This decision was driven by the fact that the performance gains from
higher-priced workstations or servers were relatively marginal compared to their
significantly higher costs. When on the road, I am often still able to do stuff
with my old Intel Macbook Pro from 2018 with an i7 and only 16GB of RAM, but
large models will overwhelm it. My workstation at home with AMD Ryzen 7 5700X
and 32GB of RAM on the other hand rarely has any problems with the models I am
working on.
For further guidance, consider the
[hardware recommendations for the Gurobi solver](https://support.gurobi.com/hc/en-us/articles/8172407217041-What-hardware-should-I-select-when-running-Gurobi-),
which are likely to be similar. Since we frequently use Gurobi in addition to
CP-SAT, our hardware choices were also influenced by their recommendations.
## A Simple Example
Before we dive into any internals, let us take a quick look at a simple
application of CP-SAT. This example is so simple that you could solve it by
hand, but know that CP-SAT would (probably) be fine with you adding a thousand
(maybe even ten- or hundred-thousand) variables and constraints more. The basic
idea of using CP-SAT is, analogous to MIPs, to define an optimization problem in
terms of variables, constraints, and objective function, and then let the solver
find a solution for it. We call such a formulation that can be understood by the
corresponding solver a _model_ for the problem. For people not familiar with
this
[declarative approach](https://programiz.pro/resources/imperative-vs-declarative-programming/),
you can compare it to SQL, where you also just state what data you want, not how
to get it. However, it is not purely declarative, because it can still make a
huge(!) difference how you model the problem and getting that right takes some
experience and understanding of the internals. You can still get lucky for
smaller problems (let us say a few hundred to thousands of variables) and obtain
optimal solutions without having an idea of what is going on. The solvers can
handle more and more 'bad' problem models effectively with every year.
> [!NOTE]
>
> A **model** in mathematical programming refers to a mathematical description
> of a problem, consisting of variables, constraints, and optionally an
> objective function that can be understood by the corresponding solver class.
> _Modelling_ refers to transforming a problem (instance) into the corresponding
> framework, e.g., by making all constraints linear as required for Mixed
> Integer Linear Programming. Be aware that the
> [SAT](https://en.wikipedia.org/wiki/SAT_solver)-community uses the term
> _model_ to refer to a (feasible) variable assignment, i.e., solution of a
> SAT-formula. If you struggle with this terminology, maybe you want to read
> this short guide on
> [Math Programming Modelling Basics](https://www.gurobi.com/resources/math-programming-modeling-basics/).
Our first problem has no deeper meaning, except for showing the basic workflow
of creating the variables (x and y), adding the constraint $x+y<=30$ on them,
setting the objective function (maximize $30x + 50y$), and obtaining a solution:
```python
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Variables
x = model.new_int_var(0, 100, "x")
y = model.new_int_var(0, 100, "y")
# Constraints
model.add(x + y <= 30)
# Objective
model.maximize(30 * x + 50 * y)
# Solve
solver = cp_model.CpSolver()
status_code = solver.solve(model)
status_name = solver.status_name()
# Print the solver status and the optimal solution.
print(f"{status_name} ({status_code})")
print(f"x={solver.value(x)}, y={solver.value(y)}")
```
OPTIMAL (4)
x=0, y=30
Pretty easy, right? For solving a generic problem, not just one specific
instance, you would of course create a dictionary or list of variables and use
something like `model.add(sum(vars)<=n)`, because you do not want to create the
model by hand for larger instances.
> [!TIP]
>
> The solver can return five different statuses:
>
> | Status | Code | Description |
> | --------------- | ---- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |
> | `UNKNOWN` | 0 | The solver has not run for long enough. |
> | `MODEL_INVALID` | 1 | The model is invalid. You will rarely see that status. |
> | `FEASIBLE` | 2 | The model has a feasible, but not necessarily optimal, solution. If your model does not have an objective, every feasible model will return `OPTIMAL`, which may be counterintuitive. |
> | `INFEASIBLE` | 3 | The model has no feasible solution. This means that your constraints are too restrictive. |
> | `OPTIMAL` | 4 | The model has an optimal solution. If your model does not have an objective, `OPTIMAL` is returned instead of `FEASIBLE`. |
>
> The status `UNBOUNDED` does _not_ exist, as CP-SAT does not have unbounded
> variables.
For larger models, CP-SAT will unfortunately not always able to compute an
optimal solution. However, the good news is that the solver will likely still
find a satisfactory solution and provide a bound on the optimal solution. Once
you reach this point, understanding how to interpret the solver's log becomes
crucial for analyzing the solver's performance. We will learn more about this
later.
### Mathematical Model
The mathematical model of the code above would usually be written by experts
something like this:
```math
\max 30x + 50y
```
```math
\text{s.t. } x+y \leq 30
```
```math
\quad 0\leq x \leq 100
```
```math
\quad 0\leq y \leq 100
```
```math
x,y \in \mathbb{Z}
```
The `s.t.` stands for `subject to`, sometimes also read as `such that`.
### Overloading
One aspect of using CP-SAT solver that often poses challenges for learners is
understanding operator overloading in Python and the distinction between the two
types of variables involved. In this context, `x` and `y` serve as mathematical
variables. That is, they are placeholders that will only be assigned specific
values during the solving phase. To illustrate this more clearly, let us explore
an example within the Python shell:
```pycon
>>> model = cp_model.CpModel()
>>> x = model.new_int_var(0, 100, "x")
>>> x
x(0..100)
>>> type(x)
>>> x + 1
sum(x(0..100), 1)
>>> x + 1 <= 1
```
In this example, `x` is not a conventional number but a placeholder defined to
potentially assume any value between 0 and 100. When 1 is added to `x`, the
result is a new placeholder representing the sum of `x` and 1. Similarly,
comparing this sum to 1 produces another placeholder, which encapsulates the
comparison of the sum with 1. These placeholders do not hold concrete values at
this stage but are essential for defining constraints within the model.
Attempting operations like `if x + 1 <= 1: print("True")` will trigger a
`NotImplementedError`, as the condition `x+1<=1` cannot be evaluated directly.
Although this approach to defining models might initially seem perplexing, it
facilitates a closer alignment with mathematical notation, which in turn can
make it easier to identify and correct errors in the modeling process.
### More examples
If you are not yet satisfied,
[this folder contains many Jupyter Notebooks with examples from the developers](https://github.com/google/or-tools/tree/stable/examples/notebook/sat).
For example
- [multiple_knapsack_sat.ipynb](https://github.com/google/or-tools/blob/stable/examples/notebook/sat/multiple_knapsack_sat.ipynb)
shows how to solve a multiple knapsack problem.
- [nurses_sat.ipynb](https://github.com/google/or-tools/blob/stable/examples/notebook/sat/nurses_sat.ipynb)
shows how to schedule the shifts of nurses.
- [bin_packing_sat.ipynb](https://github.com/google/or-tools/blob/stable/examples/notebook/sat/bin_packing_sat.ipynb)
shows how to solve a bin packing problem.
- ... (if you know more good examples I should mention here, please let me
know!)
Further, you can find an extensive and beginner-friendly example on scheduling
workers
[here](https://pganalyze.com/blog/a-practical-introduction-to-constraint-programming-using-cp-sat).
Now that you have seen a minimal model, let us explore the various options
available for problem modeling. While an experienced optimizer might be able to
handle most problems using just the elements previously discussed, clearly
expressing your intentions can help CP-SAT optimize your problem more
effectively.
---
## Basic Modeling
In this chapter, we dive into the basic modeling capabilities of CP-SAT. CP-SAT
provides an extensive set of constraints, closer to high-level modeling
languages like MiniZinc than to traditional Mixed Integer Programming (MIP). For
example, it offers constraints like `all_different` and
`add_multiplication_equality`. These advanced features reduce the need for
modeling complex logic strictly through linear constraints, though they also
increase the interface's complexity. However, not all constraints are equally
efficient; linear and boolean constraints are generally most efficient, whereas
constraints like `add_multiplication_equality` can be significantly more
resource-intensive.
> [!TIP]
>
> If you are transitioning from Mixed Integer Programming (MIP), you might be
> used to manually implementing higher-level constraints and optimizing Big-M
> parameters for better performance. With CP-SAT, such manual adjustments are
> generally unnecessary. CP-SAT operates differently from typical MIP solvers by
> relying less on linear relaxation and more on its underlying SAT-solver and
> propagators to efficiently manage logical constraints. Embrace the
> higher-level constraints—they are often more efficient in CP-SAT.
This primer has been expanded to cover all constraints across two chapters,
complete with various examples to illustrate the contexts in which they can be
used. However, mastering modeling involves much more than just an understanding
of constraints. It requires a deep appreciation of the principles and techniques
that make models effective and applicable to real-world problems.
For a more detailed exploration of modeling, consider "Model Building in
Mathematical Programming" by H. Paul Williams, which offers extensive insight
into the subject, including practical applications. While this book is not
specific to CP-SAT, the foundational techniques and concepts are broadly
applicable. Additionally, for those new to this area or transitioning from MIP
solutions, studying Gurobi's modeling approach through this
[video course](https://www.youtube.com/playlist?list=PLHiHZENG6W8CezJLx_cw9mNqpmviq3lO9)
might prove helpful. While many principles overlap, some strategies unique to
CP-SAT can better address cases where traditional MIP-solvers struggle.
Additional resources on mathematical modeling (not CP-SAT specific):
- [Math Programming Modeling Basics by Gurobi](https://www.gurobi.com/resources/math-programming-modeling-basics/):
This resource provides a solid introduction to the basics of mathematical
modeling.
- [Modeling with Gurobi Python](https://www.youtube.com/playlist?list=PLHiHZENG6W8CezJLx_cw9mNqpmviq3lO9):
A comprehensive video course on modeling with Gurobi, highlighting concepts
that are also applicable to CP-SAT.
- [Model Building in Mathematical Programming by H. Paul Williams](https://www.wiley.com/en-us/Model+Building+in+Mathematical+Programming%2C+5th+Edition-p-9781118443330):
An extensive guide to mathematical modeling techniques.
> [!TIP]
>
> For getting started with implementing optimization models in general, I highly
> recommend the blog post
> [The Art Of Not Making It An Art](https://www.gurobi.com/resources/optimization-modeling-the-art-of-not-making-it-an-art/).
> It excellently summarizes the fundamental principles of successfully managing
> an optimization project, independent of the concrete language or solver.
---
**Elements:**
- [Variables](#04-modelling-variables): `new_int_var`, `new_bool_var`,
`new_constant`, `new_int_var_series`, `new_bool_var_series`
- [Custom Domain Variables](#04-modelling-domain-variables):
`new_int_var_from_domain`
- [Objectives](#04-modelling-objectives): `minimize`, `maximize`
- [Linear Constraints](#04-modelling-linear-constraints): `add`,
`add_linear_constraint`
- [Logical Constraints (Propositional Logic)](#04-modelling-logic-constraints):
`add_implication`, `add_bool_or`, `add_at_least_one`, `add_at_most_one`,
`add_exactly_one`, `add_bool_and`, `add_bool_xor`
- [Conditional Constraints (Reification)](#04-modelling-conditional-constraints):
`only_enforce_if`
- [Absolute Values and Max/Min](#04-modelling-absmaxmin): `add_min_equality`,
`add_max_equality`, `add_abs_equality`
- [Multiplication, Division, and Modulo](#04-modelling-multdivmod):
`add_modulo_equality`, `add_multiplication_equality`, `add_division_equality`
- [All Different](#04-modelling-alldifferent): `add_all_different`
- [Domains and Combinations](#04-modelling-table): `add_allowed_assignments`,
`add_forbidden_assignments`
- [Array/Element Constraints](#04-modelling-element): `add_element`,
`add_inverse`
The more advanced constraints `add_circuit`, `add_multiple_circuit`,
`add_automaton`,`add_reservoir_constraint`,
`add_reservoir_constraint_with_active`, `new_interval_var`,
`new_interval_var_series`, `new_fixed_size_interval_var`,
`new_optional_interval_var`, `new_optional_interval_var_series`,
`new_optional_fixed_size_interval_var`,
`new_optional_fixed_size_interval_var_series`, `add_no_overlap`,
`add_no_overlap_2d`, and `add_cumulative` are discussed in the next chapter.
---
### Variables
There are two important types of variables in CP-SAT: Booleans and Integers
(which are actually converted to Booleans, but more on this later). There are
also, e.g.,
[interval variables](https://developers.google.com/optimization/reference/python/sat/python/cp_model#intervalvar),
but they are actually rather a combination of integral variables and discussed
[later](#04-modelling-intervals). For the integer variables, you have to specify
a lower and an upper bound.
```python
model = cp_model.CpModel()
# Integer variable z with bounds -100 <= z <= 100
z = model.new_int_var(-100, 100, "z") # new syntax
z_ = model.NewIntVar(-100, 100, "z_") # old syntax
# Boolean variable b
b = model.new_bool_var("b") # new syntax
b_ = model.NewBoolVar("b_") # old syntax
# Implicitly available negation of b:
not_b = ~b # will be 1 if b is 0 and 0 if b is 1
not_b_ = b.Not() # old syntax
```
Additionally, you can use `model.new_int_var_series` and
`model.new_bool_var_series` to create multiple variables at once from a pandas
Index. This is especially useful if your data is given in a pandas DataFrame.
However, there is no performance benefit in using this method, it is just more
convenient.
```python
model = cp_model.CpModel()
# Create an Index from 0 to 9
index = pd.Index(range(10), name="index")
# Create a pandas Series with 10 integer variables matching the index
xs = model.new_int_var_series("x", index, 0, 100)
# List of boolean variables
df = pd.DataFrame(
data={"weight": [1 for _ in range(10)], "value": [3 for _ in range(10)]},
index=["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"],
)
bs = model.new_bool_var_series("b", df.index) # noqa: F841
# Using the dot product on the pandas DataFrame is actually a pretty
# convenient way to create common linear expressions.
model.add(bs @ df["weight"] <= 100)
model.maximize(bs @ df["value"])
```
Additionally, there is the `new_constant`-method, which allows you to create a
variable that is constant. This allows you to safely replace variables by
constants. This is primarily useful for boolean variables, as constant integer
variables can in most cases be simply replaced by plain integers.
> [!TIP]
>
> In an older project, I observed that maintaining tight bounds on integer
> variables can significantly impact performance. Employing a heuristic to find
> a reasonable initial solution, which then allowed for tighter bounds, proved
> worthwhile, even though the bounds were just a few percent tighter. Although
> this project was several years ago and CP-SAT has advanced considerably since
> then, I still recommend keeping the bounds on the variables' ranges as tight
> as possible.
There are no continuous/floating point variables (or even constants) in CP-SAT:
If you need floating point numbers, you have to approximate them with integers
by some resolution. For example, you could simply multiply all values by 100 for
a step size of 0.01. A value of 2.35 would then be represented by 235. This
_could_ probably be implemented in CP-SAT directly, but doing it explicitly is
not difficult, and it has numerical implications that you should be aware of.
The absence of continuous variables may appear as a substantial limitation,
especially for those with a background in linear optimization where continuous
variables are typically regarded as the simpler component. However, if your
problem includes only a few continuous variables that must be approximated using
large integers and involves complex constraints such as absolute values, while
the majority of the problem is dominated by logical constraints, CP-SAT can
often outperform mixed-integer programming solvers. It is only when a problem
contains a substantial number of continuous variables and benefits significantly
from strong linear relaxation that mixed-integer programming solvers will have a
distinct advantage, despite CP-SAT having a propagator based on the dual simplex
method.
I analyzed the impact of resolution (i.e., the factor by which floating point
numbers are multiplied) on the runtime of CP-SAT, finding that the effect varied
depending on the problem. For one problem, the runtime increased only
logarithmically with the resolution, allowing the use of a very high resolution
of 100,000x without significant issues. In contrast, for another problem, the
runtime increased roughly linearly with the resolution, making high resolutions
impractical. The runtime for different factors in this case was: 1x: 0.02s, 10x:
0.7s, 100x: 7.6s, 1000x: 75s, and 10,000x: over 15 minutes, even though the
solution remained the same, merely scaled. Therefore, while high resolutions may
be feasible for some problems using CP-SAT, it is essential to verify their
influence on runtime, as the impact can be considerable.
In my experience, boolean variables are crucial in many combinatorial
optimization problems. For instance, the famous Traveling Salesman Problem
consists solely of boolean variables. Therefore, implementing a solver that
specializes in boolean variables using a SAT-solver as a foundation, such as
CP-SAT, is a sensible approach. CP-SAT leverages the strengths of SAT-solving
techniques, which are highly effective for problems dominated by boolean
variables.
You may wonder why it is necessary to explicitly name the variables in CP-SAT.
While there does not appear to be a technical reason for this requirement,
naming the variables can be extremely helpful for debugging purposes.
Understanding the naming scheme of the variables allows you to more easily
interpret the internal representation of the model, facilitating the
identification and resolution of issues. To be fair, there have only been a few
times when I actually needed to take a closer at the internal representation,
and in most of the cases I would have preferred not to have to name the
variables.
#### Custom Domain Variables
When dealing with integer variables that you know will only need to take certain
values, or when you wish to limit their possible values, custom domain variables
can become interesting. Unlike regular integer variables, which must have a
domain between a given range of values (e.g., $\[ 1, 100 \]$), domain variables
can specify a custom set of values as domain (e.g., $\\{1, 3, 5 \\}$). This
approach can enhance efficiency when the domain - the range of sensible values -
is small. However, it may not be the best choice for larger domains.
CP-SAT works by converting all integer variables into boolean variables
(warning: simplification). For each potential value, it creates two boolean
variables: one indicating whether the integer variable is equal to this value,
and another indicating whether it is less than or equal to it. This is called an
_order encoding_. At first glance, this might suggest that using domain
variables is always preferable, as it appears to reduce the number of boolean
variables needed.
However, CP-SAT employs a lazy creation strategy for these boolean variables.
This means it only generates them as needed, based on the solver's
decision-making process. Therefore, an integer variable with a wide range - say,
from 0 to 100 - will not immediately result in 200 boolean variables. It might
lead to the creation of only a few, depending on the solver's requirements.
Limiting the domain of a variable can have drawbacks. Firstly, defining a domain
explicitly can be computationally costly and increase the model size drastically
as it now need to contain not just a lower and upper bound for a variable but an
explicit list of numbers (model size is often a limiting factor). Secondly, by
narrowing down the solution space, you might inadvertently make it more
challenging for the solver to find a viable solution. First, try to let CP-SAT
handle the domain of your variables itself and only intervene if you have a good
reason to do so.
If you choose to utilize domain variables for their benefits in specific
scenarios, here is how to define them:
```python
from ortools.sat.python import cp_model
model = cp_model.CpModel()
# Define a domain with selected values
domain = cp_model.Domain.from_values([2, 5, 8, 10, 20, 50, 90])
# Can also be done via intervals
domain_2 = cp_model.Domain.from_intervals([[8, 12], [14, 20]])
# There are also some operations available
domain_3 = domain.union_with(domain_2)
# Create a domain variable within this defined domain
x = model.new_int_var_from_domain(domain, "x")
```
This example illustrates the process of creating a domain variable `x` that can
only take on the values specified in `domain`. This method is particularly
useful when you are working with variables that only have a meaningful range of
possible values within your problem's context.
### Objectives
Not every problem necessitates an objective; sometimes, finding a feasible
solution is sufficient. CP-SAT excels at finding feasible solutions, a task at
which mixed-integer programming (MIP) solvers often do not perform as well.
However, CP-SAT is also capable of effective optimization, which is an area
where older constraint programming solvers may lag, based on my experience.
CP-SAT allows for the minimization or maximization of a linear expression. You
can model more complex expressions by using auxiliary variables and additional
constraints. To specify an objective function, you can use the `model.minimize`
or `model.maximize` commands with a linear expression. This flexibility makes
CP-SAT a robust tool for a variety of optimization tasks.
```python
# Basic model with variables and constraints
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
model.add(x + 10 * y <= 100)
# Minimize 30x + 50y
model.maximize(30 * x + 50 * y)
```
Let us look on how to model more complicated expressions, using boolean
variables and generators.
```python
model = cp_model.CpModel()
x_vars = [model.new_bool_var(f"x{i}") for i in range(10)]
model.minimize(sum(i * x_vars[i] if i % 2 == 0 else i * ~x_vars[i] for i in range(10)))
```
This objective evaluates to
```math
\min \sum_{i=0}^{9} i\cdot x_i \text{ if } i \text{ is even else } i\cdot \neg x_i
```
To implement a
[lexicographic optimization](https://en.wikipedia.org/wiki/Lexicographic_optimization),
you can do multiple rounds and always fix the previous objective as constraint.
```python
# some basic model
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
model.add(x + 10 * y - 2 * z <= 100)
# Define the objectives
first_objective = 30 * x + 50 * y
second_objective = 10 * x + 20 * y + 30 * z
# Optimize for the first objective
model.maximize(first_objective)
solver = cp_model.CpSolver()
solver.solve(model)
# Fix the first objective and optimize for the second
model.add(first_objective == int(solver.objective_value)) # fix previous objective
model.minimize(second_objective) # optimize for second objective
solver.solve(model)
```
> [!TIP]
>
> You can find a more efficient implementation of lexicographic optimization in
> the _Coding Patterns_ chapter.
To handle non-linear objectives in CP-SAT, you can employ auxiliary variables
and constraints. For instance, to incorporate the absolute value of a variable
into your objective, you first create a new variable representing this absolute
value. Shortly, you will learn more about setting up these types of constraints.
Below is a Python example demonstrating how to model and minimize the absolute
value of a variable `x`:
```python
# Assuming x is already defined in your model
abs_x = model.new_int_var(
0, 100, "|x|"
) # Create a variable to represent the absolute value of x
model.add_abs_equality(target=abs_x, expr=x) # Define abs_x as the absolute value of x
model.minimize(abs_x) # Set the objective to minimize abs_x
```
The constraints available to define your feasible solution space will be
discussed in the following section.
### Linear Constraints
These are the classical constraints also used in linear optimization. Remember
that you are still not allowed to use floating point numbers within it. Same as
for linear optimization: You are not allowed to multiply a variable with
anything else than a constant and also not to apply any further mathematical
operations.
```python
model.add(10 * x + 15 * y <= 10)
model.add(x + z == 2 * y)
# This one actually is not linear but still works.
model.add(x + y != z)
# Because we are working on integers, the true smaller or greater constraints
# are trivial to implement as x < z is equivalent to x <= z-1
model.add(x < y + z)
model.add(y > 300 - 4 * z)
```
Note that `!=` can be slower than the other (`<=`, `>=`, `==`) constraints,
because it is not a linear constraint. If you have a set of mutually `!=`
variables, it is better to use `all_different` (see below) than to use the
explicit `!=` constraints.
> [!WARNING]
>
> If you use intersecting linear constraints, you may get problems because the
> intersection point needs to be integral. There is no such thing as a
> feasibility tolerance as in Mixed Integer Programming-solvers, where small
> deviations are allowed. The feasibility tolerance in MIP-solvers allows, e.g.,
> 0.763445 == 0.763439 to still be considered equal to counter numerical issues
> of floating point arithmetic. In CP-SAT, you have to make sure that values can
> match exactly.
Let us look at the following example with two linear equality constraints:
```math
x - y = 0
```
```math
4-y = 2y
```
```math
x, y \geq 0
```
You can verify that $x=4/3$ and $y=4/3$ is a feasible solution. However, coding
this in CP-SAT results in an infeasible solution:
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
model.add(x - y == 0)
model.add(4 - x == 2 * y)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE
```
Even using scaling techniques, such as multiplying integer variables by
1,000,000 to increase the resolution, would not render the model feasible. While
common linear programming solvers would handle this model without issue, CP-SAT
struggles unless modifications are made to eliminate fractions, such as
multiplying all terms by 3. However, this requires manual intervention, which
undermines the idea of using a solver. These limitations are important to
consider, although such scenarios are rare in practical applications.
> [!TIP]
>
> If you have long sums of variables and coefficients, it can be more efficient
> to use the sum-methods of LinearExpr than to use Python's sum-function. Note
> that this function does currently not support generators.
>
> ```python
> xs = [model.NewIntVar(0, 10, f"x{i}") for i in range(5)]
> weights = [i for i in range(5)]
> model.add(cp_model.LinearExpr.sum(xs) >= 1)
> model.minimize(cp_model.LinearExpr.weighted_sum(xs, weights))
> ```
If you have a lower and an upper bound for a linear expression, you can also use
the `add_linear_constraint`-method, which allows you to specify both bounds in
one go.
```python
model.add_linear_constraint(linear_expr=10 * x + 15 * y, lb=-100, ub=10)
```
The similar sounding `AddLinearExpressionInDomain` is discussed later.
### Logical Constraints (Propositional Logic)
Propositional logic allows us to describe relationships between true or false
statements using logical operators. Consider a simple scenario where we define
three Boolean variables:
```python
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b3 = model.new_bool_var("b3")
```
These variables, `b1`, `b2`, and `b3`, represent distinct propositions whose
truth values are to be determined by the model.
You can obtain the negation of a Boolean variable by using `~` or the
`.Not()`-method. The resulting variable can be used just like the original
variable:
```python
not_b1 = ~b1 # Negation of b1
not_b2 = b2.Not() # Alternative notation for negation
```
Note that you can use more than three variables in all of the following
examples, except for `add_implication` which is only defined for two variables.
> [!WARNING]
>
> Boolean variables are essentially special integer variables restricted to the
> domain of 0 and 1. Therefore, you can incorporate them into linear constraints
> as well. However, it is important to note that integer variables, unlike
> Boolean variables, cannot be used in Boolean constraints. This is a
> distinction from some programming languages, like Python, where integers can
> sometimes substitute for Booleans.
#### Adding Logical OR Constraints
The logical OR operation ensures that at least one of the specified conditions
holds true. To model this, you can use:
```python
model.add_bool_or(b1, b2, b3) # b1 or b2 or b3 must be true
model.add_at_least_one([b1, b2, b3]) # Alternative notation
model.add(b1 + b2 + b3 >= 1) # Alternative linear notation using '+' for OR
```
Both lines ensure that at least one of `b1`, `b2`, or `b3` is true.
#### Adding Logical AND Constraints
The logical AND operation specifies that all conditions must be true
simultaneously. To model conditions where `b1` is true and both `b2` and `b3`
are false, you can use:
```python
model.add_bool_and(b1, b2.Not(), b3.Not()) # b1 and not b2 and not b3 must all be true
model.add_bool_and(b1, ~b2, ~b3) # Alternative notation using '~' for negation
```
The `add_bool_and` method is most effective when used with the `only_enforce_if`
method (discussed in
[Conditional Constraints (Reification)](#04-modelling-conditional-constraints)).
For cases not utilizing `only_enforce_if` a simple AND-clause such as
$\left( b_1 \land \neg b_2 \land \neg b_3 \right)$ becomes redundant by simply
substituting $b_1$ with `1` and $b_2, b_3$ with `0`. In straightforward
scenarios, consider substituting these variables with their constant values to
reduce unnecessary complexity, especially in larger models where size and
manageability are concerns. In smaller or simpler models, CP-SAT efficiently
handles these redundancies, allowing you to focus on maintaining clarity and
readability in your model.
#### Adding Logical XOR Constraints
The logical XOR (exclusive OR) operation ensures that an odd number of operands
are true. It is crucial to understand this definition, as it has specific
implications when applied to more than two variables:
- For two variables, such as `b1 XOR b2`, the operation returns true if exactly
one of these variables is true, which aligns with the "exactly one" constraint
for this specific case.
- For three or more variables, such as in the expression `b1 XOR b2 XOR b3`, the
operation returns true if an odd number of these variables are true. This
includes scenarios where one or three variables are true, assuming the total
number of variables involved is three.
This characteristic of XOR can be somewhat complex but is crucial for modeling
scenarios where the number of true conditions needs to be odd:
```python
model.add_bool_xor(b1, b2) # Returns true if exactly one of b1 or b2 is true
model.add_bool_xor(
b1, b2, b3
) # Returns true if an odd number of b1, b2, b3 are true (i.e., one or three)
```
#### Specifying Unique Conditions
To enforce that exactly one or at most one of the variables is true, use:
```python
model.add_exactly_one([b1, b2, b3]) # Exactly one of the variables must be true
model.add_at_most_one([b1, b2, b3]) # No more than one of the variables should be true
```
These constraints are useful for scenarios where exclusive choices must be
modeled.
You could alternatively also use `add`.
```python
model.add(b1 + b2 + b3 == 1) # Exactly one of the variables must be true
model.add(b1 + b2 + b3 <= 1) # No more than one of the variables should be true
```
#### Modeling Implications
Logical implication, denoted as `->`, indicates that if the first condition is
true, the second must also be true. This can be modeled as:
```python
model.add_implication(b1, b2) # If b1 is true, then b2 must also be true
```
You could also use `add`.
```python
model.add(b2 >= b1) # If b1 is true, then b2 must also be true
```
### Conditional Constraints (Reification)
In practical applications, scenarios often arise where conditions dictate the
enforcement of certain constraints. For instance, "if this condition is true,
then a specific constraint should apply," or "if a constraint is violated, a
penalty variable is set to true, triggering another constraint." Additionally,
real-world constraints can sometimes be bypassed with financial or other types
of concessions, such as renting a more expensive truck to exceed a load limit,
or allowing a worker to take a day off after a double shift.
> In constraint programming, **reification** involves associating a Boolean
> variable with a constraint to capture its truth value, thereby turning the
> satisfaction of the constraint into a variable that can be used in further
> constraints. Full reification links a Boolean variable such that it is `True`
> if the constraint is satisfied and `False` otherwise, enabling the variable to
> be directly used in other decisions or constraints. Conversely,
> half-reification, or implied constraints, involves a one-way linkage where the
> Boolean variable being `True` implies the constraint must be satisfied, but
> its being `False` does not necessarily indicate anything about the
> constraint's satisfaction. This approach is particularly useful for expressing
> complex conditional logic and for modeling scenarios where only the
> satisfaction, and not the violation, of a constraint needs to be explicitly
> handled.
To effectively manage these conditional scenarios, CP-SAT offers the
`only_enforce_if`-method for linear and some Boolean constraints, which
activates a constraint only if a specified condition is met. This method is not
only typically more efficient than traditional methods like the
[Big-M method](https://en.wikipedia.org/wiki/Big_M_method) but also simplifies
the model by eliminating the need to determine an appropriate Big-M value.
```python
# A value representing the load that needs to be transported
load_value = model.new_int_var(0, 100, "load_value")
# ... some logic to determine the load value ...
# A variable to decide which truck to rent
truck_a = model.new_bool_var("truck_a")
truck_b = model.new_bool_var("truck_b")
truck_c = model.new_bool_var("truck_c")
# Only rent one truck
model.add_at_most_one([truck_a, truck_b, truck_c])
# Depending on which truck is rented, the load value is limited
model.add(load_value <= 50).only_enforce_if(truck_a)
model.add(load_value <= 80).only_enforce_if(truck_b)
model.add(load_value <= 100).only_enforce_if(truck_c)
# Some additional logic
driver_has_big_truck_license = model.new_bool_var("driver_has_big_truck_license")
driver_has_special_license = model.new_bool_var("driver_has_special_license")
# Only drivers with a big truck license or a special license can rent truck c
model.add_bool_or(
driver_has_big_truck_license, driver_has_special_license
).only_enforce_if(truck_c)
# Minimize the rent cost
model.minimize(30 * truck_a + 40 * truck_b + 80 * truck_c)
```
You can also use negations in the `only_enforce_if` method.
```python
model.add(x + y == 10).only_enforce_if(~b1)
```
You can also pass a list of Boolean variables to `only_enforce_if`, in which
case the constraint is only enforced if all of the variables in the list are
true.
```python
model.add(x + y == 10).only_enforce_if([b1, ~b2]) # only enforce if b1 AND NOT b2
```
> [!WARNING]
>
> While `only_enforce_if` in CP-SAT is often more efficient than similar
> concepts in classical MIP-solvers, it can still impact the performance of
> CP-SAT significantly. Doing some additional reasoning, you can often find a
> more efficient way to model your problem without having to use
> `only_enforce_if`. For logical constraints, there are actually
> straight-forward methods in
> [propositional calculus](https://en.wikipedia.org/wiki/Propositional_calculus).
> As `only_enforce_if` is often a more natural way to model your problem, it is
> still a good idea to use it to get your first prototype running and think
> about smarter ways later.
### Absolute Values and Maximum/Minimum Functions with Integer Variables
When working with integer variables in CP-SAT, operations such as computing
absolute values, maximum, and minimum values cannot be directly expressed using
basic Python operations like `abs`, `max`, or `min`. Instead, these operations
must be handled through the use of auxiliary variables and specialized
constraints that map these variables to the desired values. The auxiliary
variables can then be used in other constraints, representing the desired
subexpression.
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
# Create an auxiliary variable for the absolute value of x+z
abs_xz = model.new_int_var(0, 200, "|x+z|")
model.add_abs_equality(target=abs_xz, expr=x + z)
# Create variables to capture the maximum and minimum of x, (y-1), and z
max_xyz = model.new_int_var(0, 100, "max(x, y, z-1)")
model.add_max_equality(target=max_xyz, exprs=[x, y - 1, z])
min_xyz = model.new_int_var(-100, 100, "min(x, y, z)")
model.add_min_equality(target=min_xyz, exprs=[x, y - 1, z])
```
While some practitioners report that these methods are more efficient than those
available in classical Mixed Integer Programming solvers, such findings are
predominantly based on empirical evidence and specific use-case scenarios. It is
also worth noting that, surprisingly often, these constraints can be substituted
with more efficient linear constraints. Here is an example for achieving maximum
equality in a more efficient way:
```python
x = model.new_int_var(0, 100, "x")
y = model.new_int_var(0, 100, "y")
z = model.new_int_var(0, 100, "z")
# Ensure that max_xyz is at least the maximum of x, y, and z
max_xyz = model.new_int_var(0, 100, "max_xyz")
model.add(max_xyz >= x)
model.add(max_xyz >= y)
model.add(max_xyz >= z)
# Minimizing max_xyz to ensure it accurately reflects the maximum value
model.minimize(max_xyz)
```
This approach takes advantage of the solver's minimization function to tighten
the bound, accurately reflecting the maximum of `x`, `y`, and `z`. By utilizing
linear constraints, this method can often achieve faster solving times compared
to using the `add_max_equality` constraint. Similar techniques also exist for
managing absolute and minimum values, as well as for complex scenarios where
direct enforcement of equality through the objective function is not feasible.
### Multiplication, Division, and Modulo
In practical problems, you may need to perform more complex arithmetic
operations than simple additions. Consider the scenario where the rental cost
for a set of trucks is calculated as the product of the number of trucks, the
number of days, and the daily rental rate. Here, the first two factors are
variables, leading to a quadratic expression. Attempting to multiply two
variables directly in CP-SAT will result in an error because the `add` method
only accepts linear expressions, which are sums of variables and constants.
However, CP-SAT supports multiplication, division, and modulo operations.
Similar to using `abs`, `max`, and `min`, you must create an auxiliary variable
to represent the result of the operation.
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
xyz = model.new_int_var(-(100**3), 100**3, "x*y*z")
model.add_multiplication_equality(xyz, [x, y, z]) # xyz = x*y*z
model.add_modulo_equality(x, y, 3) # x = y % 3
model.add_division_equality(x, y, z) # x = y // z
```
When using these operations, you often transition from linear to non-linear
optimization, which is generally more challenging to solve. In cases of
division, it is essential to remember that operations are on integers;
therefore, `5 // 2` results in `2`, not `2.5`.
Many problems initially involve non-linear expressions that can often be
reformulated or approximated using linear expressions. This transformation can
enhance the tractability and speed of solving the problem. Although modeling
your problem as closely as possible to the real-world scenario is crucial, it is
equally important to balance accuracy with tractability. A highly accurate model
is futile if the solver cannot optimize it efficiently. It might be beneficial
to employ multiple phases in your optimization process, starting with a simpler,
less accurate model and gradually refining it.
Some non-linear expressions can still be managed efficiently if they are convex.
For instance, second-order cone constraints can be solved in polynomial time
using interior point methods. Gurobi, for example, supports these constraints
natively. CP-SAT includes an LP-propagator but relies on the Dual Simplex
algorithm, which is not suitable for these constraints and must depend on
simpler methods. Similarly, most open-source MIP solvers may struggle with these
constraints.
It is challenging to determine if CP-SAT can handle non-linear expressions
efficiently or which solver would be best suited for your problem. Non-linear
expressions are invariably complex, and avoiding them when possible is
advisable.
Here is one of my students' favorite examples of a non-linear expression that
can be avoided. Once introduced to mathematical notation like
$\sum_{e \in E} cost(e)\cdot x_e$, if a term depends on the combination of two
binary variables, they might initially opt for a quadratic expression such as
$\sum_{e,e'\in E} concost(e, e')\cdot x_e\cdot x_{e'}$. However, such cases can
often be modeled linearly using an auxiliary variable, avoiding the complexities
of non-linear modeling.
```python
model = cp_model.CpModel()
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b1b2 = model.new_bool_var("b1b2")
model.add_implication(~b1, ~b1b2)
model.add_implication(~b2, ~b1b2)
model.add_bool_or(~b1, ~b2, b1b2) # optional, for a penalty term to be minimized.
```
There are numerous further instances where non-linear expressions can be
simplified by using auxiliary variables or by shifting the non-linear components
into constants. However, exploring these techniques is most beneficial when you
encounter specific challenges related to non-linear expressions in your models.
We will revisit further discussions on non-linear expressions and their
conversion to piecewise linear approximations in a subsequent section. This will
provide a foundational understanding necessary for addressing more complex
modeling scenarios effectively.
### All Different
In various assignment and scheduling problems, ensuring that all variables hold
distinct values is crucial. For example, in frequency assignment, no two
transmitters within the same area should operate on the same frequency, or in
scheduling, no two tasks should occupy the same time slot. Typically, this
requirement could be modeled with a quadratic number of inequality (`!=`)
constraints. However, a more elegant solution involves using the
`add_all_different` constraint, which directly enforces that all variables in a
list take unique values. This constraint is particularly useful in solving
puzzles like Sudoku or the
[N-queens problem](https://developers.google.com/optimization/cp/queens).
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
# Adding an all-different constraint
model.add_all_different([x, y, z])
# Advanced usage with transformations
vars = [model.new_int_var(0, 10, f"v_{i}") for i in range(10)]
model.add_all_different([x + i for i, x in enumerate(vars)])
```
Using `add_all_different` not only simplifies the modeling but also utilizes a
dedicated domain-based propagator in CP-SAT, enhancing efficiency beyond what is
achievable with multiple `!=` constraints. However, if your model mixes `!=`
constraints with `add_all_different`, be cautious, as CP-SAT disables automatic
inference of `add_all_different` from groups of `!=` constraints, which can lead
to performance penalties.
For a practical demonstration, refer to the
[graph coloring problem example](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_all_different.ipynb)
in our repository. Here, using `!=` constraints solved the problem in seconds,
whereas `add_all_different` took significantly longer, illustrating the
importance of choosing the right method based on the problem scale and
complexity.
Alternatively, modeling with Boolean variables and constraints like
`add_at_most_one` or pairwise negations (`add_boolean_or(~b1, ~b2)`) can also be
effective. This approach benefits from CP-SAT's efficient handling of Boolean
logic and allows for easy integration of additional constraints or objectives,
such as licensing costs associated with certain frequencies. Although CP-SAT
does something similar internally, it creates these constructs lazily and only
as needed, whereas explicit modeling in Python may not be as efficient.
The choice between these methods—or potentially another strategy—depends on
specific model requirements and familiarity with CP-SAT's behavior. When in
doubt, start with the most intuitive method and refine your approach based on
performance observations.
### Domains and Combinations
When optimizing scenarios with predefined feasible values or combinations of
variables—often outlined in a table—it is advantageous to directly restrict the
domain of an expression or set of variables.
Consider an example where you are optimizing a shift schedule for a team of
employees, and you have a table of feasible combinations for each shift:
| Employee 1 | Employee 2 | Employee 3 | Employee 4 |
| ---------- | ---------- | ---------- | ---------- |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
In CP-SAT, this can be modeled efficiently using the `add_allowed_assignments`
method:
```python
model = cp_model.CpModel()
x_employee_1 = model.new_bool_var("x_employee_1")
x_employee_2 = model.new_bool_var("x_employee_2")
x_employee_3 = model.new_bool_var("x_employee_3")
x_employee_4 = model.new_bool_var("x_employee_4")
# Define the allowed assignments
allowed_assignments = [
[1, 0, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1],
[0, 1, 0, 1],
]
model.add_allowed_assignments(
[x_employee_1, x_employee_2, x_employee_3, x_employee_4], allowed_assignments
)
```
Alternatively, forbidden combinations can be specified using
`add_forbidden_assignments`:
```python
prohibit_assignments = [
[1, 0, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1],
[0, 1, 0, 1],
]
model.add_forbidden_assignments(
[x_employee_1, x_employee_2, x_employee_3, x_employee_4], prohibit_assignments
)
```
The utility of the `add_allowed_assignments` method becomes more apparent when
integrated with other constraints within the model, rather than when it spans
all variables. If the table covered all variables, one could theoretically
evaluate each row to identify the best solution without the need for
sophisticated optimization techniques. However, consider this scenario where
constraints are integrated across multiple shifts:
```python
NUM_SHIFTS = 7
model = cp_model.CpModel()
x_employee_1 = [model.new_bool_var(f"x_employee_1_{i}") for i in range(NUM_SHIFTS)]
x_employee_2 = [model.new_bool_var(f"x_employee_2_{i}") for i in range(NUM_SHIFTS)]
x_employee_3 = [model.new_bool_var(f"x_employee_3_{i}") for i in range(NUM_SHIFTS)]
x_employee_4 = [model.new_bool_var(f"x_employee_4_{i}") for i in range(NUM_SHIFTS)]
for i in range(NUM_SHIFTS):
model.add_allowed_assignments(
[x_employee_1[i], x_employee_2[i], x_employee_3[i], x_employee_4[i]],
allowed_assignments,
)
# ... some further constraints and objectives to connect the days ...
# ... if the days would be independent, you would solve each day separately ...
```
The `add_allowed_assignments` method in CP-SAT enables the direct incorporation
of specific feasible combinations into your optimization model, ensuring that
only certain configurations of variables are considered within the solution
space. This method effectively "hard-codes" these configurations, simplifying
the model by predefining which combinations of variables are permissible, much
like setting rules for employee shifts or resource allocations.
> [!NOTE]
>
> Hardcoding specific combinations in your model is a preliminary step toward
> advanced decomposition techniques like Dantzig-Wolfe decomposition. In this
> method, a complex optimization problem is simplified by replacing a group of
> correlated variables with composite variables. Such a composite variable
> represents a solution for a subproblem. Optimizing these composite variables
> in the master problem significantly reduces the model's complexity and
> improves the efficiency of solving large-scale problems.
A related method for managing linear expressions instead of direct assignments
is `add_linear_expression_in_domain`. Suppose we know a certain linear
expression, \(10x + 5y\), must equal 20, 50, or 100:
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
domain = cp_model.Domain.from_values([20, 50, 100])
model.add_linear_expression_in_domain(10 * x + 5 * y, domain)
```
> [!WARNING]
>
> Ensure calculations are correct, especially when working with integers, to
> avoid creating an infeasible or overly restrictive model. Consider using an
> auxiliary variable with a restricted domain and softer constraints (`<=`,
> `>=`) to achieve a more flexible and forgiving model setup.
### Element/Array Constraints
Before exploring specialized constraints, let us examine the last of the generic
ones. The element constraint facilitates accessing the value of a variable (or
since ortools 9.12, a linear expression) within an array using another variable
as the index. Accessing a variable in an array with a constant index is
straightforward; however, integrating a variable index into your model adds
complexity. This constraint can also be used to ensure that a variable matches
the value at a specific array position.
```python
model = cp_model.CpModel()
x = model.new_int_var(-100, 100, "x")
y = model.new_int_var(-100, 100, "y")
z = model.new_int_var(-100, 100, "z")
var_array = [x, y, z]
# Create a variable for the index and a variable for the value at that index.
index_var = model.new_int_var(0, len(var_array) - 1, "index")
value_at_index_var = model.new_int_var(-100, 100, "value_at_index")
# Apply the element constraint to link the index and value variables.
model.add_element(expressions=var_array, index=index_var, target=value_at_index_var)
# CAVEAT: Before ortools 9.12, it was `variables=` instead of `expressions=`.
```
Examples of feasible variable assignments:
| `x` | `y` | `z` | `index_var` | `value_at_index` |
| --- | --- | --- | ----------- | ---------------- |
| 3 | 4 | 5 | 0 | 3 |
| 3 | 4 | 5 | 1 | 4 |
| 3 | 4 | 5 | 2 | 5 |
| 7 | 3 | 4 | 0 | 7 |
The subsequent constraint resembles a stable matching in array form. For two
equally sized arrays of variables $v$ and $w$, each of size $|v|$, it imposes a
bijective relationship: $v[i]=j \Leftrightarrow w[j]=i$ for all
$i,j \in 0,\ldots,|v|-1$. This constraint limits the variables' values to
$0,\ldots, |v|-1$.
```python
model = cp_model.CpModel()
v = [model.new_int_var(0, 5, f"v_{i}") for i in range(6)]
w = [model.new_int_var(0, 5, f"w_{i}") for i in range(6)]
model.add_inverse(v, w)
```
Examples of feasible variable assignments:
| array | 0 | 1 | 2 | 3 | 4 | 5 |
| ----- | --- | --- | --- | --- | --- | --- |
| v | 0 | 1 | 2 | 3 | 4 | 5 |
| w | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 0 | 1 | 2 | 3 | 4 | 5 |
| ----- | --- | --- | --- | --- | --- | --- |
| v | 1 | 2 | 3 | 4 | 5 | 0 |
| w | 5 | 0 | 1 | 2 | 3 | 4 |
| array | 0 | 1 | 2 | 3 | 4 | 5 |
| ----- | --- | --- | --- | --- | --- | --- |
| v | 1 | 0 | 3 | 5 | 2 | 4 |
| w | 1 | 0 | 4 | 2 | 5 | 3 |
| 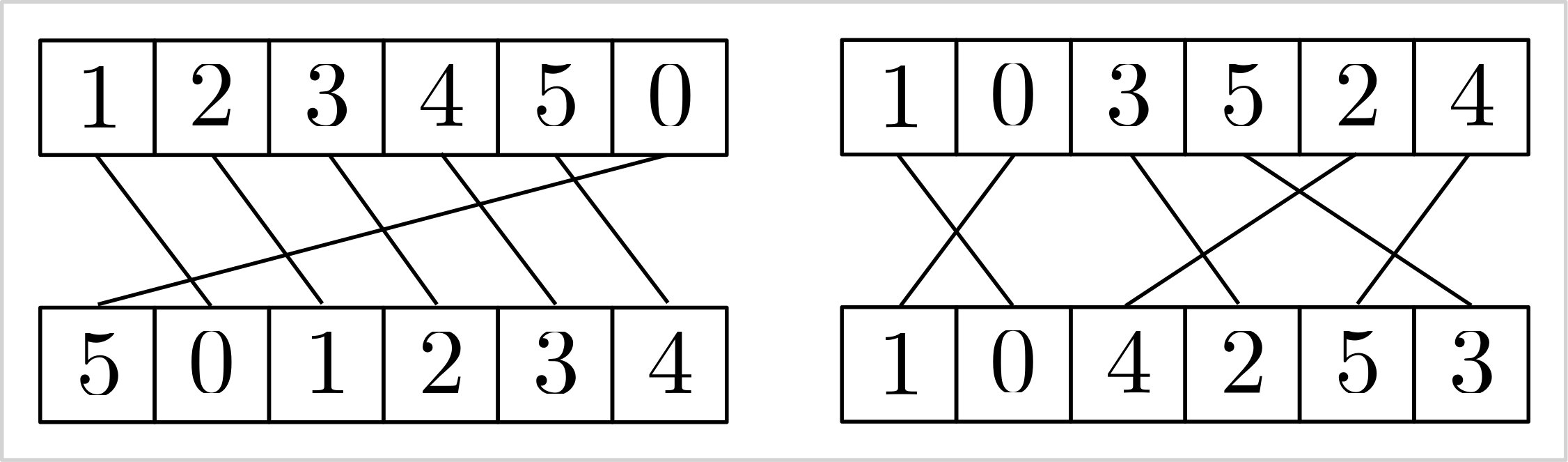 |
| :--------------------------------------------------------------------------------------------------: |
| Visualizing the stable matching induced by the `add_inverse` constraint. |
> [!WARNING]
>
> I generally advise against using the `add_element` and `add_inverse`
> constraints. While CP-SAT may have effective propagation techniques for them,
> these constraints can appear unnatural and complex. It's often more
> straightforward to model stable matching with binary variables $x_{ij}$,
> indicating whether $v_i$ is matched with $w_j$, and employing an
> `add_exactly_one` constraint for each vertex to ensure unique matches. If your
> model needs to capture specific attributes or costs associated with
> connections, binary variables are necessary. Relying solely on indices would
> require additional logic for accurate representation. Additionally, use
> non-binary variables only if the numerical value inherently carries semantic
> meaning that cannot simply be re-indexed.
## Advanced Modeling
After having seen the basic elements of CP-SAT, this chapter will introduce you
to the more complex constraints. These constraints are already focused on
specific problems, such as routing or scheduling, but very generic and powerful
within their domain. However, they also need more explanation on the correct
usage.
- [Tour Constraints](#04-modelling-circuit): `add_circuit`,
`add_multiple_circuit`, `add_reservoir_constraint_with_active`
- [Intervals](#04-modelling-intervals): `new_interval_var`,
`new_interval_var_series`, `new_fixed_size_interval_var`,
`new_optional_interval_var`, `new_optional_interval_var_series`,
`new_optional_fixed_size_interval_var`,
`new_optional_fixed_size_interval_var_series`,
`add_no_overlap`,`add_no_overlap_2d`, `add_cumulative`
- [Automaton Constraints](#04-modelling-automaton): `add_automaton`
- [Reservoir Constraints](#04-modelling-reservoir): `add_reservoir_constraint`,
- [Piecewise Linear Constraints](#04-modelling-pwl): Not officially part of
CP-SAT, but we provide some free copy&pasted code to do it.
### Circuit/Tour-Constraints
Routes and tours are essential in addressing optimization challenges across
various fields, far beyond traditional routing issues. For example, in DNA
sequencing, optimizing the sequence in which DNA fragments are assembled is
crucial, while in scientific research, methodically ordering the reconfiguration
of experiments can greatly reduce operational costs and downtime. The
`add_circuit` and `add_multiple_circuit` constraints in CP-SAT allow you to
easily model various scenarios. These constraints extend beyond the classical
[Traveling Salesman Problem (TSP)](https://en.wikipedia.org/wiki/Travelling_salesman_problem),
allowing for solutions where not every node needs to be visited and
accommodating scenarios that require multiple disjoint sub-tours. This
adaptability makes them invaluable for a broad spectrum of practical problems
where the sequence and arrangement of operations critically impact efficiency
and outcomes.
|  |
| :-------------------------------------------------------------------------------------------------------------------------------------------------: |
| The Traveling Salesman Problem (TSP) asks for the shortest possible route that visits every vertex exactly once and returns to the starting vertex. |
The Traveling Salesman Problem is one of the most famous and well-studied
combinatorial optimization problems. It is a classic example of a problem that
is easy to understand, common in practice, but hard to solve. It also has a
special place in the history of optimization, as many techniques that are now
used generally were first developed for the TSP. If you have not done so yet, I
recommend watching
[this talk by Bill Cook](https://www.youtube.com/watch?v=5VjphFYQKj8), or even
reading the book
[In Pursuit of the Traveling Salesman](https://press.princeton.edu/books/paperback/9780691163529/in-pursuit-of-the-traveling-salesman).
> [!TIP]
>
> If your problem is specifically the Traveling Salesperson Problem (TSP), you
> might find the
> [Concorde solver](https://www.math.uwaterloo.ca/tsp/concorde.html)
> particularly effective. For problems closely related to the TSP, a Mixed
> Integer Programming (MIP) solver may be more suitable, as many TSP variants
> yield strong linear programming relaxations that MIP solvers can efficiently
> exploit. Additionally, consider
> [OR-Tools Routing](https://developers.google.com/optimization/routing) if
> routing constitutes a significant aspect of your problem. However, for
> scenarios where variants of the TSP are merely a component of a larger
> problem, utilizing CP-SAT with the `add_circuit` or `add_multiple_circuit`
> constraints can be very beneficial.
|  |
| :-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| This example shows why Mixed Integer Programming solvers are so good in solving the TSP. The linear relaxation (at the top) is already very close to the optimal solution. By branching, i.e., trying 0 and 1, on just two fractional variables, we not only find the optimal solution but can also prove optimality. The example was generated with the [DIY TSP Solver](https://www.math.uwaterloo.ca/tsp/D3/bootQ.html). |
#### `add_circuit`
The `add_circuit` constraint is utilized to solve circuit problems within
directed graphs, even allowing loops. It operates by taking a list of triples
`(u,v,var)`, where `u` and `v` denote the source and target vertices,
respectively, and `var` is a Boolean variable that indicates if an edge is
included in the solution. The constraint ensures that the edges marked as `True`
form a single circuit visiting each vertex exactly once, aside from vertices
with a loop set as `True`. Vertex indices should start at 0 and must not be
skipped to avoid isolation and infeasibility in the circuit.
Here is an example using the CP-SAT solver to address a directed Traveling
Salesperson Problem (TSP):
```python
from ortools.sat.python import cp_model
# Directed graph with weighted edges
dgraph = {(0, 1): 13, (1, 0): 17, ...(2, 3): 27}
# Initialize CP-SAT model
model = cp_model.CpModel()
# Boolean variables for each edge
edge_vars = {(u, v): model.new_bool_var(f"e_{u}_{v}") for (u, v) in dgraph.keys()}
# Circuit constraint for a single tour
model.add_circuit([(u, v, var) for (u, v), var in edge_vars.items()])
# Objective function to minimize total cost
model.minimize(sum(dgraph[(u, v)] * x for (u, v), x in edge_vars.items()))
# Solve model
solver = cp_model.CpSolver()
status = solver.solve(model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
tour = [(u, v) for (u, v), x in edge_vars.items() if solver.value(x)]
print("Tour:", tour)
# Output: [(0, 1), (2, 0), (3, 2), (1, 3)], i.e., 0 -> 1 -> 3 -> 2 -> 0
```
This constraint can be adapted for paths by adding a virtual enforced edge that
closes the path into a circuit, such as `(3, 0, 1)` for a path from vertex 0 to
vertex 3.
#### Creative usage of `add_circuit`
The `add_circuit` constraint can be creatively adapted to solve various related
problems. While there are more efficient algorithms for solving the Shortest
Path Problem, let us demonstrate how to adapt the `add_circuit` constraint for
educational purposes.
```python
from ortools.sat.python import cp_model
# Define a weighted, directed graph with edge costs
dgraph = {(0, 1): 13, (1, 0): 17, ...(2, 3): 27}
source_vertex = 0
target_vertex = 3
# Add zero-cost loops for vertices not being the source or target
for v in [1, 2]:
dgraph[(v, v)] = 0
# Initialize CP-SAT model and variables
model = cp_model.CpModel()
edge_vars = {(u, v): model.new_bool_var(f"e_{u}_{v}") for (u, v) in dgraph}
# Define the circuit including a pseudo-edge from target to source
circuit = [(u, v, var) for (u, v), var in edge_vars.items()] + [
(target_vertex, source_vertex, 1)
]
model.add_circuit(circuit)
# Minimize total cost
model.minimize(sum(dgraph[(u, v)] * x for (u, v), x in edge_vars.items()))
# Solve and extract the path
solver = cp_model.CpSolver()
status = solver.solve(model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
path = [(u, v) for (u, v), x in edge_vars.items() if solver.value(x) and u != v]
print("Path:", path)
# Output: [(0, 1), (1, 3)], i.e., 0 -> 1 -> 3
```
This approach showcases the flexibility of the `add_circuit` constraint for
various tour and path problems. Explore further examples:
- [Budget constrained tours](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_circuit_budget.py):
Optimize the largest possible tour within a specified budget.
- [Multiple tours](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_circuit_multi_tour.py):
Solve for $k$ minimal tours covering all vertices.
#### `add_multiple_circuit`
You can model multiple disjoint tours using several `add_circuit` constraints,
as demonstrated in
[this example](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_circuit_multi_tour.py).
If all tours share a common depot (vertex 0), the `add_multiple_circuit`
constraint is an alternative. However, this constraint does not allow you to
specify the number of tours, nor can it determine to which tour a particular
edge belongs. Therefore, the `add_circuit` constraint is often a superior
choice. Although the arguments for both constraints are identical, vertex 0
serves a unique role as the depot where all tours commence and conclude.
#### Performance of `add_circuit` for the TSP
The table below displays the performance of the CP-SAT solver on various
instances of the TSPLIB, using the `add_circuit` constraint, under a 90-second
time limit. The performance can be considered reasonable, but can be easily
beaten by a Mixed Integer Programming solver.
| Instance | # vertices | runtime | lower bound | objective | opt. gap |
| :------- | ---------: | ------: | ----------: | --------: | -------: |
| att48 | 48 | 0.47 | 33522 | 33522 | 0 |
| eil51 | 51 | 0.69 | 426 | 426 | 0 |
| st70 | 70 | 0.8 | 675 | 675 | 0 |
| eil76 | 76 | 2.49 | 538 | 538 | 0 |
| pr76 | 76 | 54.36 | 108159 | 108159 | 0 |
| kroD100 | 100 | 9.72 | 21294 | 21294 | 0 |
| kroC100 | 100 | 5.57 | 20749 | 20749 | 0 |
| kroB100 | 100 | 6.2 | 22141 | 22141 | 0 |
| kroE100 | 100 | 9.06 | 22049 | 22068 | 0 |
| kroA100 | 100 | 8.41 | 21282 | 21282 | 0 |
| eil101 | 101 | 2.24 | 629 | 629 | 0 |
| lin105 | 105 | 1.37 | 14379 | 14379 | 0 |
| pr107 | 107 | 1.2 | 44303 | 44303 | 0 |
| pr124 | 124 | 33.8 | 59009 | 59030 | 0 |
| pr136 | 136 | 35.98 | 96767 | 96861 | 0 |
| pr144 | 144 | 21.27 | 58534 | 58571 | 0 |
| kroB150 | 150 | 58.44 | 26130 | 26130 | 0 |
| kroA150 | 150 | 90.94 | 26498 | 26977 | 2% |
| pr152 | 152 | 15.28 | 73682 | 73682 | 0 |
| kroA200 | 200 | 90.99 | 29209 | 29459 | 1% |
| kroB200 | 200 | 31.69 | 29437 | 29437 | 0 |
| pr226 | 226 | 74.61 | 80369 | 80369 | 0 |
| gil262 | 262 | 91.58 | 2365 | 2416 | 2% |
| pr264 | 264 | 92.03 | 49121 | 49512 | 1% |
| pr299 | 299 | 92.18 | 47709 | 49217 | 3% |
| linhp318 | 318 | 92.45 | 41915 | 52032 | 19% |
| lin318 | 318 | 92.43 | 41915 | 52025 | 19% |
| pr439 | 439 | 94.22 | 105610 | 163452 | 35% |
There are two prominent formulations to model the Traveling Salesman Problem
(TSP) without an `add_circuit` constraint: the
[Dantzig-Fulkerson-Johnson (DFJ) formulation](https://en.wikipedia.org/wiki/Travelling_salesman_problem#Dantzig%E2%80%93Fulkerson%E2%80%93Johnson_formulation)
and the
[Miller-Tucker-Zemlin (MTZ) formulation](https://en.wikipedia.org/wiki/Travelling_salesman_problem#Miller%E2%80%93Tucker%E2%80%93Zemlin_formulation[21]).
The DFJ formulation is generally regarded as more efficient due to its stronger
linear relaxation. However, it requires lazy constraints, which are not
supported by the CP-SAT solver. When implemented without lazy constraints, the
performance of the DFJ formulation is comparable to that of the MTZ formulation
in CP-SAT. Nevertheless, both formulations perform significantly worse than the
`add_circuit` constraint. This indicates the superiority of using the
`add_circuit` constraint for handling tours and paths in such problems. Unlike
end users, the `add_circuit` constraint can utilize lazy constraints internally,
offering a substantial advantage in solving the TSP.
### Scheduling and Packing with Intervals
A special case of variables are the interval variables, that allow to model
intervals, i.e., a span of some length with a start and an end. There are fixed
length intervals, flexible length intervals, and optional intervals to model
various use cases. These intervals become interesting in combination with the
no-overlap constraints for 1D and 2D. We can use this for geometric packing
problems, scheduling problems, and many other problems, where we have to prevent
overlaps between intervals. These variables are special because they are
actually not a variable, but a container that bounds separately defined start,
length, and end variables.
There are four types of interval variables: `new_interval_var`,
`new_fixed_size_interval_var`, `new_optional_interval_var`, and
`new_optional_fixed_size_interval_var`. The `new_optional_interval_var` is the
most expressive but also the most expensive, while `new_fixed_size_interval_var`
is the least expressive and the easiest to optimize. All four types take a
`start=` variable. Intervals with `fixed_size` in their name require a constant
`size=` argument defining the interval length. Otherwise, the `size=` argument
can be a variable in combination with an `end=` variable, which complicates the
solution. Intervals with `optional` in their name include an `is_present=`
argument, a boolean indicating if the interval is present. The no-overlap
constraints, discussed later, apply only to intervals that are present, allowing
for modeling problems with multiple resources or optional tasks. Instead of a
pure integer variable, all arguments also accept an affine expression, e.g.,
`start=5*start_var+3`.
```python
model = cp_model.CpModel()
start_var = model.new_int_var(0, 100, "start")
length_var = model.new_int_var(10, 20, "length")
end_var = model.new_int_var(0, 100, "end")
is_present_var = model.new_bool_var("is_present")
# creating an interval whose length can be influenced by a variable (more expensive)
flexible_interval = model.new_interval_var(
start=start_var, size=length_var, end=end_var, name="flexible_interval"
)
# creating an interval of fixed length
fixed_interval = model.new_fixed_size_interval_var(
start=start_var,
size=10, # needs to be a constant
name="fixed_interval",
)
# creating an interval that can be present or not and whose length can be influenced by a variable (most expensive)
optional_interval = model.new_optional_interval_var(
start=start_var,
size=length_var,
end=end_var,
is_present=is_present_var,
name="optional_interval",
)
# creating an interval that can be present or not
optional_fixed_interval = model.new_optional_fixed_size_interval_var(
start=start_var,
size=10, # needs to be a constant
is_present=is_present_var,
name="optional_fixed_interval",
)
```
These interval variables are not useful on their own, as we could have easily
achieved the same with a simple linear constraint. However, CP-SAT provides
special constraints for these interval variables, that would actually be much
harder to model by hand and are also much more efficient.
CP-SAT offers the following three constraints for intervals:
`add_no_overlap`,`add_no_overlap_2d`, `add_cumulative`. `add_no_overlap` is used
to prevent overlaps between intervals on a single dimension, e.g., time.
`add_no_overlap_2d` is used to prevent overlaps between intervals on two
dimensions, e.g., for packing rectangles. `add_cumulative` is used to model a
resource constraint, where the sum of the demands of the overlapping intervals
must not exceed the capacity of the resource.
The `add_no_overlap` constraints takes a list of (optional) interval variables
and ensures that no two present intervals overlap.
```python
model.add_no_overlap(
interval_vars=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
]
)
```
The `add_no_overlap_2d` constraints takes two lists of (optional) interval and
ensures that for every `i` and `j` either `x_intervals[i]` and `x_intervals[j]`
or `y_intervals[i]` and `y_intervals[j]` do not overlap. Thus, both lists must
have the same length as `x_intervals[i]` and `y_intervals[i]` are considered
belonging together. If either `x_intervals[i]` or `y_intervals[i]` are optional,
the whole object is optional.
```python
model.add_no_overlap_2d(
x_intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
],
y_intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
# ...
],
)
```
The `add_cumulative` constraint is used to model a resource constraint, where
the sum of the demands of the overlapping intervals must not exceed the capacity
of the resource. An example could be scheduling the usage of certain energy
intensive machines, where the sum of the energy demands must not exceed the
capacity of the power grid. It takes a list of intervals, a list of demands, and
a capacity variable. The list of demands must have the same length as the list
of intervals, as the demands of the intervals are matched by index. As capacity
and demands can be variables (or affine expressions), quite complex resource
constraints can be modeled.
```python
demand_vars = [model.new_int_var(1, 10, f"demand_{i}") for i in range(4)]
capacity_var = model.new_int_var(1, 100, "capacity")
model.add_cumulative(
intervals=[
flexible_interval,
fixed_interval,
optional_interval,
optional_fixed_interval,
],
demands=demand_vars,
capacity=capacity_var,
)
```
> [!WARNING]
>
> Do not directly jump to intervals when you have a scheduling problem.
> Intervals are great if you actually have a somewhat continuous time or space
> that you need to schedule. If you have a more discrete problem, such as a
> scheduling problem with a fixed number of slots, you can often model this
> problem much more efficiently using simple Boolean variables and constraints.
> Especially if you can use domain knowledge to find clusters of meetings that
> cannot overlap, this can be much more efficient. If the scheduling is
> dominated by the transitions, your scheduling problem may actually be a
> routing problems, for which the `add_circuit` constraint is more suitable.
Let us examine a few examples of how to use these constraints effectively.
#### Scheduling for a Conference Room with Intervals
Assume we have a conference room and need to schedule several meetings. Each
meeting has a fixed length and a range of possible start times. The time slots
are in 5-minute intervals starting at 8:00 AM and ending at 6:00 PM. Thus, there
are $10 \times 12 = 120$ time slots, and we can use a simple integer variable to
model the start time. With fixed meeting lengths, we can use the
`new_fixed_size_interval_var` to model the intervals. The `add_no_overlap`
constraint ensures no two meetings overlap, and domains for the start time can
model the range of possible start times.
To handle input data, let us define a `namedtuple` to store the meeting and two
functions to convert between time and index.
```python
# Convert time to index and back
def t_to_idx(hour, minute):
return (hour - 8) * 12 + minute // 5
def idx_to_t(time_idx):
hour = 8 + time_idx // 12
minute = (time_idx % 12) * 5
return f"{hour}:{minute:02d}"
# Define meeting information using namedtuples
MeetingInfo = namedtuple("MeetingInfo", ["start_times", "duration"])
```
Then let us create a few meetings we want to schedule.
```python
# Meeting definitions
meetings = {
"meeting_a": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(12, 0)],
[t_to_idx(16, 0), t_to_idx(17, 0)],
],
duration=120 // 5, # 2 hours
),
"meeting_b": MeetingInfo(
start_times=[
[t_to_idx(10, 0), t_to_idx(12, 0)],
],
duration=30 // 5, # 30 minutes
),
"meeting_c": MeetingInfo(
start_times=[
[t_to_idx(16, 0), t_to_idx(17, 0)],
],
duration=15 // 5, # 15 minutes
),
"meeting_d": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(10, 0)],
[t_to_idx(12, 0), t_to_idx(14, 0)],
],
duration=60 // 5, # 1 hour
),
}
```
Now we can create the CP-SAT model and add the intervals and constraints.
```python
# Create a new CP-SAT model
model = cp_model.CpModel()
# Create start time variables for each meeting
start_time_vars = {
meeting_name: model.new_int_var_from_domain(
cp_model.Domain.from_intervals(meeting_info.start_times),
f"start_{meeting_name}",
)
for meeting_name, meeting_info in meetings.items()
}
# Create interval variables for each meeting
interval_vars = {
meeting_name: model.new_fixed_size_interval_var(
start=start_time_vars[meeting_name],
size=meeting_info.duration,
name=f"interval_{meeting_name}",
)
for meeting_name, meeting_info in meetings.items()
}
# Ensure that now two meetings overlap
model.add_no_overlap(list(interval_vars.values()))
```
And finally, we can solve the model and extract the solution.
```python
# Solve the model
solver = cp_model.CpSolver()
status = solver.solve(model)
# Extract and print the solution
scheduled_times = {}
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
for meeting_name in meetings:
start_time = solver.value(start_time_vars[meeting_name])
scheduled_times[meeting_name] = start_time
print(f"{meeting_name} starts at {idx_to_t(start_time)}")
else:
print("No feasible solution found.")
```
Doing some quick magic with matplotlib, we can visualize the schedule.
|  |
| :-----------------------------------------------------------------------------------------------------------------------------------: |
| A possible non-overlapping schedule for the above example. The instance is quite simple, but you could try adding some more meetings. |
#### Scheduling for Multiple Resources with Optional Intervals
Now, imagine we have multiple resources, such as multiple conference rooms, and
we need to schedule the meetings such that no two meetings overlap in the same
room. This can be modeled with optional intervals, where the intervals exist
only if the meeting is scheduled in the room. The `add_no_overlap` constraint
ensures that no two meetings overlap in the same room.
Because we now have two rooms, we need to create a more challenging instance
first. Otherwise, the solver may not need to use both rooms. We do this by
simply adding more and longer meetings.
```python
# Meeting definitions
meetings = {
"meeting_a": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(12, 0)],
[t_to_idx(16, 0), t_to_idx(16, 0)],
],
duration=120 // 5,
),
"meeting_b": MeetingInfo(
start_times=[[t_to_idx(10, 0), t_to_idx(12, 0)]], duration=240 // 5
),
"meeting_c": MeetingInfo(
start_times=[[t_to_idx(16, 0), t_to_idx(17, 0)]], duration=30 // 5
),
"meeting_d": MeetingInfo(
start_times=[
[t_to_idx(8, 0), t_to_idx(10, 0)],
[t_to_idx(12, 0), t_to_idx(14, 0)],
],
duration=60 // 5,
),
"meeting_e": MeetingInfo(
start_times=[[t_to_idx(10, 0), t_to_idx(12, 0)]], duration=120 // 5
),
"meeting_f": MeetingInfo(
start_times=[[t_to_idx(14, 0), t_to_idx(14, 0)]], duration=240 // 5
),
"meeting_g": MeetingInfo(
start_times=[[t_to_idx(14, 0), t_to_idx(16, 0)]], duration=120 // 5
),
}
```
This time, we need to create an interval variable for each room and meeting, as
well as a Boolean variable indicating if the meeting is scheduled in the room.
We cannot use the same interval variable for multiple rooms, as otherwise the
interval would be present in both rooms.
```python
# Create the model
model = cp_model.CpModel()
# Create start time and room variables
start_time_vars = {
name: model.new_int_var_from_domain(
cp_model.Domain.from_intervals(info.start_times), f"start_{name}"
)
for name, info in meetings.items()
}
rooms = ["room_a", "room_b"]
room_vars = {
name: {room: model.new_bool_var(f"{name}_in_{room}") for room in rooms}
for name in meetings
}
# Create interval variables and add no-overlap constraint
interval_vars = {
name: {
# We need a separate interval for each room
room: model.new_optional_fixed_size_interval_var(
start=start_time_vars[name],
size=info.duration,
is_present=room_vars[name][room],
name=f"interval_{name}_in_{room}",
)
for room in rooms
}
for name, info in meetings.items()
}
```
Now we can enforce that each meeting is assigned to exactly one room and that
there is no overlap between meetings in the same room.
```python
# Ensure each meeting is assigned to exactly one room
for name, room_dict in room_vars.items():
model.add_exactly_one(room_dict.values())
for room in rooms:
model.add_no_overlap([interval_vars[name][room] for name in meetings])
```
Again, doing some quick magic with matplotlib, we get the following schedule.
| 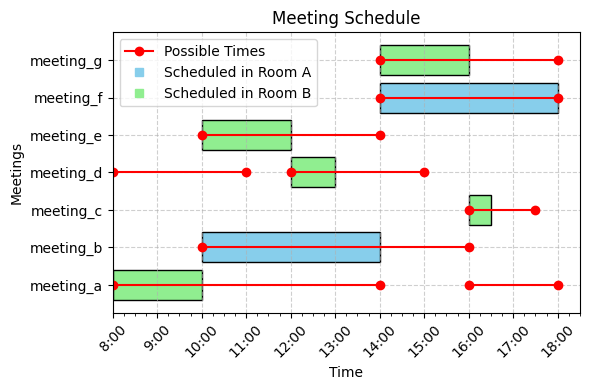 |
| :-------------------------------------------------------------------------------------------------------------------------------: |
| A possible non-overlapping schedule for the above example with multiple rooms. |
> [!TIP]
>
> You could easily extend this model to schedule as many meetings as possible
> using an objective function. You could also maximize the distance between two
> meetings by using a variable size interval. This would be a good exercise to
> try.
#### Packing rectangles without overlaps
Let us examine how to check if a set of rectangles can be packed into a
container without overlaps. This is a common problem in logistics, where boxes
must be packed into a container, or in cutting stock problems, where pieces are
cut from a larger material.
First, we define namedtuples for the rectangles and the container.
```python
from collections import namedtuple
# Define namedtuples for rectangles and container
Rectangle = namedtuple("Rectangle", ["width", "height"])
Container = namedtuple("Container", ["width", "height"])
# Example usage
rectangles = [Rectangle(width=2, height=3), Rectangle(width=4, height=5)]
container = Container(width=10, height=10)
```
Next, we create variables for the bottom-left corners of the rectangles. These
variables are constrained to ensure the rectangles remain within the container.
```python
model = cp_model.CpModel()
# Create variables for the bottom-left corners of the rectangles
x_vars = [
model.new_int_var(0, container.width - box.width, name=f"x1_{i}")
for i, box in enumerate(rectangles)
]
y_vars = [
model.new_int_var(0, container.height - box.height, name=f"y1_{i}")
for i, box in enumerate(rectangles)
]
```
Next, we create interval variables for each rectangle. The start of these
intervals corresponds to the bottom-left corner, and the size is the width or
height of the rectangle. We use the `add_no_overlap_2d` constraint to ensure
that no two rectangles overlap.
```python
# Create interval variables representing the width and height of the rectangles
x_interval_vars = [
model.new_fixed_size_interval_var(
start=x_vars[i], size=box.width, name=f"x_interval_{i}"
)
for i, box in enumerate(rectangles)
]
y_interval_vars = [
model.new_fixed_size_interval_var(
start=y_vars[i], size=box.height, name=f"y_interval_{i}"
)
for i, box in enumerate(rectangles)
]
# Ensure no two rectangles overlap
model.add_no_overlap_2d(x_interval_vars, y_interval_vars)
```
The optional intervals with flexible length allow us to model rotations and find
the largest possible packing. The code may appear complex, but it remains
straightforward considering the problem's complexity.
First, we define namedtuples for the rectangles and the container.
```python
from collections import namedtuple
from ortools.sat.python import cp_model
# Define namedtuples for rectangles and container
Rectangle = namedtuple("Rectangle", ["width", "height", "value"])
Container = namedtuple("Container", ["width", "height"])
# Example usage
rectangles = [
Rectangle(width=2, height=3, value=1),
Rectangle(width=4, height=5, value=1),
]
container = Container(width=10, height=10)
```
Next, we create variables for the coordinates of the rectangles. This includes
variables for the bottom-left and top-right corners, as well as a boolean
variable to indicate if a rectangle is rotated.
```python
model = cp_model.CpModel()
# Create variables for the bottom-left and top-right corners of the rectangles
bottom_left_x_vars = [
model.new_int_var(0, container.width, name=f"x1_{i}")
for i, box in enumerate(rectangles)
]
bottom_left_y_vars = [
model.new_int_var(0, container.height, name=f"y1_{i}")
for i, box in enumerate(rectangles)
]
upper_right_x_vars = [
model.new_int_var(0, container.width, name=f"x2_{i}")
for i, box in enumerate(rectangles)
]
upper_right_y_vars = [
model.new_int_var(0, container.height, name=f"y2_{i}")
for i, box in enumerate(rectangles)
]
# Create variables to indicate if a rectangle is rotated
rotated_vars = [model.new_bool_var(f"rotated_{i}") for i in range(len(rectangles))]
```
We then create variables for the width and height of each rectangle, adjusting
for rotation. Constraints ensure these variables are set correctly based on
whether the rectangle is rotated.
```python
# Create variables for the width and height, adjusted for rotation
width_vars = []
height_vars = []
for i, box in enumerate(rectangles):
domain = cp_model.Domain.from_values([box.width, box.height])
width_vars.append(model.new_int_var_from_domain(domain, name=f"width_{i}"))
height_vars.append(model.new_int_var_from_domain(domain, name=f"height_{i}"))
# There are two possible assignments for width and height
model.add_allowed_assignments(
[width_vars[i], height_vars[i], rotated_vars[i]],
[(box.width, box.height, 0), (box.height, box.width, 1)],
)
```
Next, we create a boolean variable indicating if a rectangle is packed or not,
and then interval variables representing its occupied space in the container.
These intervals are used to enforce the no-overlap constraint.
```python
# Create variables indicating if a rectangle is packed
packed_vars = [model.new_bool_var(f"packed_{i}") for i in range(len(rectangles))]
# Create interval variables representing the width and height of the rectangles
x_interval_vars = [
model.new_optional_interval_var(
start=bottom_left_x_vars[i],
size=width_vars[i],
is_present=packed_vars[i],
end=upper_right_x_vars[i],
name=f"x_interval_{i}",
)
for i, box in enumerate(rectangles)
]
y_interval_vars = [
model.new_optional_interval_var(
start=bottom_left_y_vars[i],
size=height_vars[i],
is_present=packed_vars[i],
end=upper_right_y_vars[i],
name=f"y_interval_{i}",
)
for i, box in enumerate(rectangles)
]
# Ensure no two rectangles overlap
model.add_no_overlap_2d(x_interval_vars, y_interval_vars)
```
Finally, we maximize the number of packed rectangles by defining an objective
function.
```python
# Maximize the number of packed rectangles
model.maximize(sum(box.value * x for x, box in zip(packed_vars, rectangles)))
```
|  |
| :----------------------------------------------------------------------------------------------------------------------------------------------------: |
| This dense packing was found by CP-SAT in less than 0.3s, which is quite impressive and seems to be more efficient than a naive Gurobi implementation. |
You can find the full code here:
| Problem Variant | Code |
| :------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| Deciding feasibility of packing rectangles without rotations | [./evaluations/packing/solver/packing_wo_rotations.py](https://github.com/d-krupke/cpsat-primer/blob/main/evaluations/packing/solver/packing_wo_rotations.py) |
| Finding the largest possible packing of rectangles without rotations | [./evaluations/packing/solver/knapsack_wo_rotations.py](https://github.com/d-krupke/cpsat-primer/blob/main/evaluations/packing/solver/knapsack_wo_rotations.py) |
| Deciding feasibility of packing rectangles with rotations | [./evaluations/packing/solver/packing_with_rotations.py](https://github.com/d-krupke/cpsat-primer/blob/main/evaluations/packing/solver/packing_with_rotations.py) |
| Finding the largest possible packing of rectangles with rotations | [./evaluations/packing/solver/knapsack_with_rotations.py](https://github.com/d-krupke/cpsat-primer/blob/main/evaluations/packing/solver/knapsack_with_rotations.py) |
CP-SAT is good at finding a feasible packing, but incapable of proving
infeasibility in most cases. When using the knapsack variant, it can still pack
most of the rectangles even for the larger instances.
|  |
| :------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| The number of solved instances for the packing problem (90s time limit). Rotations make things slightly more difficult. None of the used instances were proved infeasible. |
|  |
| However, CP-SAT is able to pack nearly all rectangles even for the largest instances. |
#### Resolution and Parameters
In earlier versions of CP-SAT, the performance of no-overlap constraints was
greatly influenced by the resolution. This impact has evolved, yet it remains
somewhat inconsistent. In a notebook example, I explored how resolution affects
the execution time of the no-overlap constraint in versions 9.3 and 9.8 of
CP-SAT. For version 9.3, there is a noticeable increase in execution time as the
resolution grows. Conversely, in version 9.8, execution time actually reduces
when the resolution is higher, a finding supported by repeated tests. This
unexpected behavior suggests that the performance of CP-SAT regarding no-overlap
constraints has not stabilized and may continue to vary in upcoming versions.
| Resolution | Runtime (CP-SAT 9.3) | Runtime (CP-SAT 9.8) |
| ---------- | -------------------- | -------------------- |
| 1x | 0.02s | 0.03s |
| 10x | 0.7s | 0.02s |
| 100x | 7.6s | 1.1s |
| 1000x | 75s | 40.3s |
| 10_000x | >15min | 0.4s |
[This notebook](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_no_overlap_2d.ipynb)
was used to create the table above.
However, while playing around with less documented features, I noticed that the
performance for the older version can be improved drastically with the following
parameters:
```python
solver.parameters.use_energetic_reasoning_in_no_overlap_2d = True
solver.parameters.use_timetabling_in_no_overlap_2d = True
solver.parameters.use_pairwise_reasoning_in_no_overlap_2d = True
```
With the latest version of CP-SAT, I did not notice a significant difference in
performance when using these parameters.
### Automaton Constraints
Automaton constraints model finite state machines, enabling the representation
of feasible transitions between states. This is particularly useful in software
verification, where it is essential to ensure that a program follows a specified
sequence of states. Given the critical importance of verification in research,
there is likely a dedicated audience that appreciates this constraint. However,
others may prefer to proceed to the next section.
| 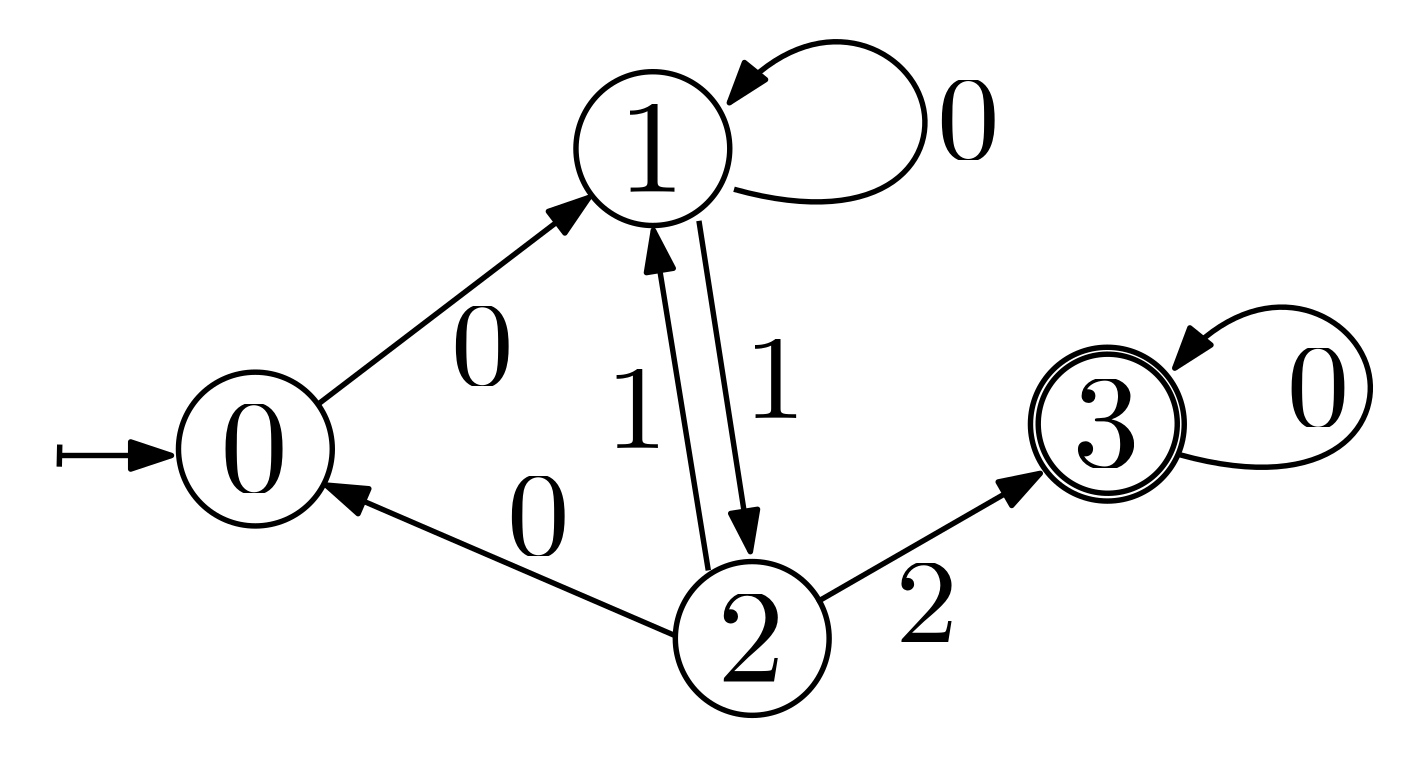 |
| :----------------------------------------------------------------------------------------------------------------------------------------: |
| An example of a finite state machine with four states and seven transitions. State 0 is the initial state, and state 3 is the final state. |
The automaton operates as follows: We have a list of integer variables
`transition_variables` that represent the transition values. Starting from the
`starting_state`, the next state is determined by the transition triple
`(state, transition_value, next_state)` matching the first transition variable.
If no such triple is found, the model is infeasible. This process repeats for
each subsequent transition variable. It is crucial that the final transition
leads to a final state (possibly via a loop); otherwise, the model remains
infeasible.
The state machine from the example can be modeled as follows:
```python
model = cp_model.CpModel()
transition_variables = [model.new_int_var(0, 2, f"transition_{i}") for i in range(4)]
transition_triples = [
(0, 0, 1), # If in state 0 and the transition value is 0, go to state 1
(1, 0, 1), # If in state 1 and the transition value is 0, stay in state 1
(1, 1, 2), # If in state 1 and the transition value is 1, go to state 2
(2, 0, 0), # If in state 2 and the transition value is 0, go to state 0
(2, 1, 1), # If in state 2 and the transition value is 1, go to state 1
(2, 2, 3), # If in state 2 and the transition value is 2, go to state 3
(3, 0, 3), # If in state 3 and the transition value is 0, stay in state 3
]
model.add_automaton(
transition_variables=transition_variables,
starting_state=0,
final_states=[3],
transition_triples=transition_triples,
)
```
The assignment `[0, 1, 2, 0]` would be a feasible solution for this model,
whereas the assignment `[1, 0, 1, 2]` would be infeasible because state 0 has no
transition for value 1. Similarly, the assignment `[0, 0, 1, 1]` would be
infeasible as it does not end in a final state.
### Reservoir Constraints
Sometimes, we need to keep the balance between inflows and outflows of a
reservoir. The name giving example is a water reservoir, where we need to keep
the water level between a minimum and a maximum level. The reservoir constraint
takes a list of time variables, a list of integer level changes, and the minimum
and maximum level of the reservoir. If the affine expression `times[i]` is
assigned a value `t`, then the current level changes by `level_changes[i]`. Note
that at the moment, variable level changes are not supported, which means level
changes are constant at time `t`. The constraint ensures that the level stays
between the minimum and maximum level at all time, i.e.
`sum(level_changes[i] if times[i] <= t) in [min_level, max_level]`.
There are many other examples apart from water reservoirs, where you need to
balance demands and supplies, such as maintaining a certain stock level in a
warehouse, or ensuring a certain staffing level in a clinic. The
`add_reservoir_constraint` constraint in CP-SAT allows you to model such
problems easily.
In the following example, `times[i]` represents the time at which the change
`level_changes[i]` will be applied, thus both lists needs to be of the same
length. The reservoir level starts at 0, and the minimum level has to be
$\leq 0$ and the maximum level has to be $\geq 0$.
```python
times = [model.new_int_var(0, 10, f"time_{i}") for i in range(10)]
level_changes = [1] * 10
model.add_reservoir_constraint(
times=times,
level_changes=level_changes,
min_level=-10,
max_level=10,
)
```
Additionally, the `add_reservoir_constraint_with_active` constraint allows you
to model a reservoir with _optional_ changes. Here, we additionally have a list
of Boolean variables `actives`, where `actives[i]` indicates if the change
`level_changes[i]` takes place, i.e. if
`sum(level_changes[i] * actives[i] if times[i] <= t) in [min_level, max_level]`
If a change is not active, it is as if it does not exist, and the reservoir
level remains the same, independent of the time and change values.
```python
times = [model.new_int_var(0, 10, f"time_{i}") for i in range(10)]
level_changes = [1] * 10
actives = [model.new_bool_var(f"active_{i}") for i in range(10)]
model.add_reservoir_constraint_with_active(
times=times,
level_changes=level_changes,
actives=actives,
min_level=-10,
max_level=10,
)
```
To illustrate the usage of the reservoir constraint, we look at an example for
scheduling nurses in a clinic. For the full example, take a look at the
[notebook](https://github.com/d-krupke/cpsat-primer/blob/main/examples/add_reservoir.ipynb).
The clinic needs to ensure that there are always enough nurses available without
over-staffing too much. For a 12-hour work day, we model the demands for nurses
as integers for each hour of the day.
```python
# a positive number means we need more nurses, a negative number means we need fewer nurses.
demand_change_at_t = [3, 0, 0, 0, 2, 0, 0, 0, -1, 0, -1, 0, -3]
demand_change_times = list(range(len(demand_change_at_t))) # [0, 1, ..., 12]
```
We have a list of nurses, each with an individual availability as well as a
maximum shift length.
```python
max_shift_length = 5
# begin and end of the availability of each nurse
nurse_availabilities = 2 * [
(0, 7),
(0, 4),
(0, 8),
(2, 9),
(1, 5),
(5, 12),
(7, 12),
(0, 12),
(4, 12),
]
```
We now initialize all relevant variables of the model. Each nurse is assigned a
start and end time of their shift as well as a Boolean variable indicating if
they are working at all.
```python
# boolean variable to indicate if a nurse is scheduled
nurse_scheduled = [
model.new_bool_var(f"nurse_{i}_scheduled") for i in range(len(nurse_availabilities))
]
# model the begin and end of each shift
shifts_begin = [
model.new_int_var(begin, end, f"begin_nurse_{i}")
for i, (begin, end) in enumerate(nurse_availabilities)
]
shifts_end = [
model.new_int_var(begin, end, f"end_nurse_{i}")
for i, (begin, end) in enumerate(nurse_availabilities)
]
```
We now add some basic constraints to ensure that the shifts are valid.
```python
for begin, end in zip(shifts_begin, shifts_end):
model.add(end >= begin) # make sure the end is after the begin
model.add(end - begin <= max_shift_length) # make sure, the shifts are not too long
```
Our reservoir level is the number of nurses scheduled at any time minus the
demand for nurses up until that point. We can now add the reservoir constraint
to ensure that we have enough nurses available at all times while not having too
many nurses scheduled (i.e., the reservoir level is between 0 and 2). We have
three types of changes in the reservoir:
1. The demand for nurses changes at the beginning of each hour. For these we use
fixed integer times and activate all changes. Note that the demand changes
are negated, as an increase in demand lowers the reservoir level.
2. If a nurse begins a shift, we increase the reservoir level by 1. We use the
`shifts_begin` variables as times and change the reservoir level only if the
nurse is scheduled.
3. Once a nurse ends a shift, we decrease the reservoir level by 1. We use the
`shifts_end` variables as times and change the reservoir level only if the
nurse is scheduled.
```python
times = demand_change_times
demands = [
-demand for demand in demand_change_at_t
] # an increase in demand lowers the reservoir
actives = [1] * len(demand_change_times)
times += list(shifts_begin)
demands += [1] * len(shifts_begin) # a nurse begins a shift
actives += list(nurse_scheduled)
times += list(shifts_end)
demands += [-1] * len(shifts_end) # a nurse ends a shift
actives += list(nurse_scheduled)
model.add_reservoir_constraint_with_active(
times=times,
level_changes=demands,
min_level=0,
max_level=2,
actives=actives,
)
```
> [!NOTE]
>
> The reservoir constraints can express conditions that are difficult to model
> "by hand". However, while I do not have much experience with them, I would not
> expect them to be particularly easy to optimize. Let me know if you have
> either good or bad experiences with them in practice and for which problem
> scales they work well.
### Non-Linear Constraints/Piecewise Linear Functions
In practice, you often have cost functions that are not linear. For example,
consider a production problem where you have three different items you produce.
Each item has different components, you have to buy. The cost of the components
will first decrease with the amount you buy, then at some point increase again
as your supplier will be out of stock and you have to buy from a more expensive
supplier. Additionally, you only have a certain amount of customers willing to
pay a certain price for your product. If you want to sell more, you will have to
lower the price, which will decrease your profit.
Let us assume such a function looks like $y=f(x)$ in the following figure.
Unfortunately, it is a rather complex function that we cannot directly express
in CP-SAT. However, we can approximate it with a piecewise linear function as
shown in red. Such piecewise linear approximations are very common, and some
solvers can even do them automatically, e.g., Gurobi. The resolution can be
arbitrarily high, but the more segments you have, the more complex the model
becomes. Thus, it is usually only chosen to be as high as necessary.
|  |
| :-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| We can model an arbitrary continuous function with a piecewise linear function. Here, we split the original function into a number of straight segments. The accuracy can be adapted to the requirements. The linear segments can then be expressed in CP-SAT. The fewer such segments, the easier it remains to model and solve. |
Using linear constraints (`model.add`) and reification (`.only_enforce_if`), we
can model such a piecewise linear function in CP-SAT. For this we simply use
boolean variables to decide for a segment, and then activate the corresponding
linear constraint via reification. However, this has two problems in CP-SAT, as
shown in the next figure.
|  |
| :---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| Even if the function f(x) now consists of linear segments, we cannot simply implement $y=f(x)$ in CP-SAT. First, for many $x$-values, $f(x)$ will be not integral and, thus, infeasible. Second, the canonical representation of many linear segments will require non-integral coefficients, which are also not allowed in CP-SAT. |
- **Problem A:** Even if we can express a segment as a linear function, the
result of the function may not be integral. In the example, $f(5)$ would be
$3.5$ and, thus, if we enforce $y=f(x)$, $x$ would be prohibited to be $5$,
which is not what we want. There are two options now. Either, we use a more
complex piecewise linear approximation that ensures that the function will
always yield integral solutions or we use inequalities instead. The first
solution has the issue that this can require too many segments, making it far
too expensive to optimize. The second solution will be a weaker constraint as
now we can only enforce $y<=f(x)$ or $y>=f(x)$, but not $y=f(x)$. If you try
to enforce it by $y<=f(x)$ and $y>=f(x)$, you will end with the same
infeasibility as before. However, often an inequality will be enough. If the
problem is to prevent $y$ from becoming too large, you use $y<=f(x)$, if the
problem is to prevent $y$ from becoming too small, you use $y>=f(x)$. If we
want to represent the costs by $f(x)$, we would use $y>=f(x)$ to minimize the
costs.
- **Problem B:** The canonical representation of a linear function is $y=ax+b$.
However, this will often require non-integral coefficients. Luckily, we can
automatically scale them up to integral values by adding a scaling factor. The
inequality $y=0.5x+0.5$ in the example can also be represented as $2y=x+1$. I
will spare you the math, but it just requires a simple trick with the least
common multiple. Of course, the required scaling factor can become large, and
at some point lead to overflows.
An implementation could now look as follows:
```python
# We want to enforce y=f(x)
x = model.new_int_var(0, 7, "x")
y = model.new_int_var(0, 5, "y")
# use boolean variables to decide for a segment
segment_active = [model.new_bool_var("segment_1"), model.new_bool_var("segment_2")]
model.add_at_most_one(segment_active) # enforce one segment to be active
# Segment 1
# if 0<=x<=3, then y >= 0.5*x + 0.5
model.add(2 * y >= x + 1).only_enforce_if(segment_active[0])
model.add(x >= 0).only_enforce_if(segment_active[0])
model.add(x <= 3).only_enforce_if(segment_active[0])
# Segment 2
model.add(_SLIGHTLY_MORE_COMPLEX_INEQUALITY_).only_enforce_if(segment_active[1])
model.add(x >= 3).only_enforce_if(segment_active[1])
model.add(x <= 7).only_enforce_if(segment_active[1])
model.minimize(y)
# if we were to maximize y, we would have used <= instead of >=
```
This can be quite tedious, but luckily, I wrote a small helper class that will
do this automatically for you. You can find it in
[./utils/piecewise_functions](https://github.com/d-krupke/cpsat-primer/blob/main/utils/piecewise_functions/).
Simply copy it into your code.
This code does some further optimizations:
1. Considering every segment as a separate case can be quite expensive and
inefficient. Thus, it can make a serious difference if you can combine
multiple segments into a single case. This can be achieved by detecting
convex ranges, as the constraints of convex areas do not interfere with each
other.
2. Adding the convex hull of the segments as a redundant constraint that does
not depend on any `only_enforce_if` can in some cases help the solver to find
better bounds. `only_enforce_if`-constraints are often not very good for the
linear relaxation, and having the convex hull as independent constraint can
directly limit the solution space, without having to do any branching on the
cases.
Let us use this code to solve an instance of the problem above.
We have two products that each require three components. The first product
requires 3 of component 1, 5 of component 2, and 2 of component 3. The second
product requires 2 of component 1, 1 of component 2, and 3 of component 3. We
can buy up to 1500 of each component for the price given in the figure below. We
can produce up to 300 of each product and sell them for the price given in the
figure below.
|  |  |
| :--------------------------------------------------------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------------------------------------------------------: |
| Costs for buying components necessary for production. | Selling price for the products. |
We want to maximize the profit, i.e., the selling price minus the costs for
buying the components. We can model this as follows:
```python
requirements_1 = (3, 5, 2)
requirements_2 = (2, 1, 3)
from ortools.sat.python import cp_model
model = cp_model.CpModel()
buy_1 = model.new_int_var(0, 1_500, "buy_1")
buy_2 = model.new_int_var(0, 1_500, "buy_2")
buy_3 = model.new_int_var(0, 1_500, "buy_3")
produce_1 = model.new_int_var(0, 300, "produce_1")
produce_2 = model.new_int_var(0, 300, "produce_2")
model.add(produce_1 * requirements_1[0] + produce_2 * requirements_2[0] <= buy_1)
model.add(produce_1 * requirements_1[1] + produce_2 * requirements_2[1] <= buy_2)
model.add(produce_1 * requirements_1[2] + produce_2 * requirements_2[2] <= buy_3)
# You can find this code it ./utils!
from piecewise_functions import PiecewiseLinearFunction, PiecewiseLinearConstraint
# Define the functions for the costs
costs_1 = [(0, 0), (1000, 400), (1500, 1300)]
costs_2 = [(0, 0), (300, 300), (700, 500), (1200, 600), (1500, 1100)]
costs_3 = [(0, 0), (200, 400), (500, 700), (1000, 900), (1500, 1500)]
# PiecewiseLinearFunction is a pydantic model and can be serialized easily!
f_costs_1 = PiecewiseLinearFunction(
xs=[x for x, y in costs_1], ys=[y for x, y in costs_1]
)
f_costs_2 = PiecewiseLinearFunction(
xs=[x for x, y in costs_2], ys=[y for x, y in costs_2]
)
f_costs_3 = PiecewiseLinearFunction(
xs=[x for x, y in costs_3], ys=[y for x, y in costs_3]
)
# Define the functions for the gain
gain_1 = [(0, 0), (100, 800), (200, 1600), (300, 2_000)]
gain_2 = [(0, 0), (80, 1_000), (150, 1_300), (200, 1_400), (300, 1_500)]
f_gain_1 = PiecewiseLinearFunction(xs=[x for x, y in gain_1], ys=[y for x, y in gain_1])
f_gain_2 = PiecewiseLinearFunction(xs=[x for x, y in gain_2], ys=[y for x, y in gain_2])
# Create y>=f(x) constraints for the costs
x_costs_1 = PiecewiseLinearConstraint(model, buy_1, f_costs_1, upper_bound=False)
x_costs_2 = PiecewiseLinearConstraint(model, buy_2, f_costs_2, upper_bound=False)
x_costs_3 = PiecewiseLinearConstraint(model, buy_3, f_costs_3, upper_bound=False)
# Create y<=f(x) constraints for the gain
x_gain_1 = PiecewiseLinearConstraint(model, produce_1, f_gain_1, upper_bound=True)
x_gain_2 = PiecewiseLinearConstraint(model, produce_2, f_gain_2, upper_bound=True)
# Maximize the gain minus the costs
model.Maximize(x_gain_1.y + x_gain_2.y - (x_costs_1.y + x_costs_2.y + x_costs_3.y))
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
status = solver.solve(model)
print(f"Buy {solver.value(buy_1)} of component 1")
print(f"Buy {solver.value(buy_2)} of component 2")
print(f"Buy {solver.value(buy_3)} of component 3")
print(f"Produce {solver.value(produce_1)} of product 1")
print(f"Produce {solver.value(produce_2)} of product 2")
print(f"Overall gain: {solver.objective_value}")
```
This will give you the following output:
```
Buy 930 of component 1
Buy 1200 of component 2
Buy 870 of component 3
Produce 210 of product 1
Produce 150 of product 2
Overall gain: 1120.0
```
Unfortunately, these problems quickly get very complicated to model and solve.
This is just a proof that, theoretically, you can model such problems in CP-SAT.
Practically, you can lose a lot of time and sanity with this if you are not an
expert.
## Parameters
The CP-SAT solver offers numerous parameters to control its behavior. These
parameters are implemented via
[Protocol Buffers](https://developers.google.com/protocol-buffers) and can be
manipulated using the `parameters` member. To explore all available options,
refer to the well-documented `proto` file in the
[official repository](https://github.com/google/or-tools/blob/stable/ortools/sat/sat_parameters.proto).
Below, I will highlight the most important parameters so you can get the most
out of CP-SAT.
> :warning: Only a few parameters, such as `max_time_in_seconds`, are suitable
> for beginners. Most other parameters, like decision strategies, are best left
> at their default settings, as they are well-chosen and tampering with them
> could disrupt optimizations. For better performance, focus on improving your
> model.
### Logging
The `log_search_progress` parameter is crucial at the beginning. It enables
logging of the search progress, providing insights into how CP-SAT solves your
problem. While you may deactivate it later for production, it is beneficial
during development to understand the process and respond to any issues.
```python
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
# Custom log function, for example, using the Python logging module instead of stdout
# Useful in a Jupyter notebook, where logging to stdout might not be visible
solver.log_callback = print # (str)->None
# If using a custom log function, you can disable logging to stdout
solver.parameters.log_to_stdout = False
```
The log offers valuable information for understanding CP-SAT and your
optimization problem. It details aspects such as how many variables were
directly removed and which techniques most effectively contributed to improving
lower and upper bounds.
An example log might look like this:
```
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
1.94e-05s 0.00e+00d [DetectDifferentVariables]
1.90e-04s 8.39e-06d [ProcessSetPPC] #relevant_constraints=560 #num_inclusions=24
2.01e-05s 0.00e+00d [FindAlmostIdenticalLinearConstraints]
...
```
Given the complexity of the log, I developed a tool to visualize and comment on
it. You can copy and paste your log into the tool, which will automatically
highlight the most important details. Be sure to check out the examples.
[](https://cpsat-log-analyzer.streamlit.app/)
[](https://github.com/d-krupke/CP-SAT-Log-Analyzer)
|  |
| :-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| A plot of the search progress over time as visualized by the log analyzer using information from the log (a different log than displayed above). This plot helps you understand which part of your problem is more challenging: finding a good solution or proving its quality. Based on this, you can implement appropriate countermeasures. |
We will revisit the logs in the next chapter.
> [!TIP]
>
> From my experience as a lecturer, I often encounter students who believe
> CP-SAT is stuck, only to discover that their model building includes an
> unnecessarily complex $O(n^5)$ nested loop, which would take days to run. It
> is natural to assume that the issue lies with CP-SAT because it handles the
> hard part of solving the problem. However, even the seemingly simple part of
> model building can consume a lot of time if implemented incorrectly. By
> enabling logging, students could immediately see that the issue lies in their
> own code rather than with CP-SAT. This simple step can save a lot of time and
> frustration.
### Time Limit and Status
When working with large or complex models, the CP-SAT solver may not always
reach an optimal solution within a reasonable time frame and could potentially
run indefinitely. Therefore, setting a time limit is advisable, particularly in
a production environment, to prevent the solver from running endlessly. Even
within a time limit, CP-SAT often finds a reasonably good solution, although it
may not be proven optimal.
Determining an appropriate time limit depends on various factors and usually
requires some experimentation. I typically start with a time limit between 60
and 300 seconds, as this provides a balance between not having to wait too long
during model testing and giving the solver enough time to find a good solution.
To set a time limit (in seconds) before running the solver, use the following
command:
```python
solver.parameters.max_time_in_seconds = 60 # 60s time limit
```
After running the solver, it is important to check the status to determine
whether an optimal solution, a feasible solution, or no solution at all has been
found:
```python
status = solver.solve(model)
if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
print("We have a solution.")
else:
print("Help?! No solution available! :( ")
```
The possible status codes are:
- `OPTIMAL` (4): An optimal solution has been found.
- `FEASIBLE` (2): A feasible solution has been found, and a bound may be
available to assess its quality via `solver.best_objective_bound`.
- `INFEASIBLE` (3): No solution can satisfy all constraints.
- `MODEL_INVALID` (1): The CP-SAT model is incorrectly specified.
- `UNKNOWN` (0): No solution was found, and no infeasibility proof is available.
A bound may still be available.
To get the name from the status code, use `solver.status_name(status)`.
In addition to limiting runtime, you can specify acceptable solution quality
using `absolute_gap_limit` and `relative_gap_limit`. The absolute limit stops
the solver when the solution is within a specified value of the bound. The
relative limit stops the solver when the objective value (O) is within a
specified ratio of the bound (B). To stop when the solution is (provably) within
5% of the optimum, use:
```python
solver.parameters.relative_gap_limit = 0.05
```
For cases where progress stalls or for other reasons, solution callbacks can be
used to halt the solver. With these, you can decide on every new solution if the
solution is good enough or if the solver should continue searching for a better
one. Unlike Gurobi, CP-SAT does not support adding lazy constraints from these
callbacks (or at all), which is a significant limitation for problems requiring
dynamic model adjustments.
To add a solution callback, inherit from the base class
`CpSolverSolutionCallback`. Documentation for this base class and its operations
is available
[here](https://developers.google.com/optimization/reference/python/sat/python/cp_model#cp_model.CpSolverSolutionCallback).
```python
class MySolutionCallback(cp_model.CpSolverSolutionCallback):
def __init__(self, data):
cp_model.CpSolverSolutionCallback.__init__(self)
self.data = data # Store data in the callback.
def on_solution_callback(self):
obj = self.objective_value # Best solution value
bound = self.best_objective_bound # Best bound
print(f"The current value of x is {self.Value(x)}")
if abs(obj - bound) < 10:
self.StopSearch() # Stop search for a better solution
# ...
solver.solve(model, MySolutionCallback(None))
```
An
[official example using callbacks](https://github.com/google/or-tools/blob/stable/ortools/sat/samples/stop_after_n_solutions_sample_sat.py)
is available.
> [!WARNING]
>
> Bounds in optimization can be a double-edged sword. On one hand, they indicate
> how close you are to the optimal solution within your chosen model, and they
> allow you to terminate the optimization process early if the solution is
> sufficiently close. On the other hand, they can be misleading for two key
> reasons. First, the bounds pertain to the optimization model and may give a
> false sense of quality, as neither the model nor the data are typically
> perfect. Second, in some cases, obtaining good bounds within a reasonable time
> may be impossible, yet the solution might still be good—you simply may not
> realize it. This can lead to wasted resources as you pursue tighter models or
> better approaches with little to no real benefit. While bounds are extremely
> useful, it is important to understand their origin and limitations, and not
> regard them as the final determinant of solution quality.
Besides querying the objective value of the best solution and the best known
bound, you can also access internal metrics such as `self.num_booleans`,
`self.num_branches`, and `self.num_conflicts`. These metrics will be discussed
later.
As of version 9.10, CP-SAT also supports bound callbacks, which are triggered
when the proven bound improves. Unlike solution callbacks, which activate upon
finding new solutions, bound callbacks are useful for stopping the search when
the bound is sufficiently good. The syntax for bound callbacks differs from that
of solution callbacks, as they are implemented as free functions that directly
access the solver object.
```python
solver = cp_model.CpSolver()
def bound_callback(bound):
print(f"New bound: {bound}")
if bound > 100:
solver.stop_search()
solver.best_bound_callback = bound_callback
```
Instead of using a simple function, you can also use a callable object to store
a reference to the solver object. This approach allows you to define the
callback outside the local scope, providing greater flexibility.
```python
class BoundCallback:
def __init__(self, solver) -> None:
self.solver = solver
def __call__(self, bound):
print(f"New bound: {bound}")
if bound > 200:
print("Abort search due to bound")
self.solver.stop_search()
```
This method is more flexible than the solution callback and can be considered
more Pythonic.
Additionally, whenever there is a new solution or bound, a log message is
generated. You can hook into the log output to decide when to stop the search
using CP-SAT's log callback.
```python
solver.parameters.log_search_progress = True # Enable logging
solver.log_callback = lambda msg: print("LOG:", msg) # (str) -> None
```
> [!WARNING]
>
> Be careful when using callbacks, as they can slow down the solver
> significantly. Callbacks are often called frequently, forcing a switch back to
> the slower Python layer. I have often seen students frustrated by slow solver
> performance, only to discover that most of the solver's time is spent in the
> callback function. Even if the operations within the callback are not complex,
> the time spent can add up quickly and affect overall performance.
### Parallelization
CP-SAT is a portfolio-solver that uses different techniques to solve the
problem. There is some information exchange between the different workers, but
it does not split the solution space into different parts, thus, it does not
parallelize the branch-and-bound algorithm as MIP-solvers do. This can lead to
some redundancy in the search, but running different techniques in parallel will
also increase the chance of running the right technique. Predicting which
technique will be the best for a specific problem is often hard, thus, this
parallelization can be quite useful.
By default, CP-SAT leverages all available cores (including hyperthreading). You
can control the parallelization of CP-SAT by setting the number of search
workers.
```python
solver.parameters.num_workers = 8 # use 8 cores
```
> [!TIP]
>
> For many models, you can boost performance by manually reducing the number of
> workers to match the number of physical cores, or even fewer. This can be
> beneficial for several reasons: it allows the remaining workers to run at a
> higher frequency, provides more memory bandwidth, and reduces potential
> interference between workers. However, be aware that reducing the number of
> workers might also decrease the overall chance of one of them making progress,
> as there are fewer directions being explored simultaneously.
Here are the solvers used by CP-SAT 9.9 on different parallelization levels for
an optimization problem and no additional specifications (e.g., decision
strategies). Each row describes the addition of various solvers with respect to
the previous row. Note that some parameters/constraints/objectives can change
the parallelization strategy. Also check
[the official documentation](https://github.com/google/or-tools/blob/main/ortools/sat/docs/troubleshooting.md#improving-performance-with-multiple-workers).
| # Workers | Full Problem Subsolvers | First Solution Subsolvers | Incomplete Subsolvers | Helper Subsolvers |
| --------- | ------------------------------------------------------------------------------ | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------- |
| **1** | `default_lp` | No solver | No solver | No solver |
| **2** | | | +13 solvers: `feasibility_pump`, `graph_arc_lns`, `graph_cst_lns`, `graph_dec_lns`, `graph_var_lns`, `packing_precedences_lns`, `packing_rectangles_lns`, `packing_slice_lns`, `rins/rens`, `rnd_cst_lns`, `rnd_var_lns`, `scheduling_precedences_lns`, `violation_ls` | +3 solvers: `neighborhood_helper`, `synchronization_agent`, `update_gap_integral` |
| **3** | +1 solver: `no_lp` | | | |
| **4** | +1 solver: `max_lp` | | | |
| **5** | | +1 solver: `fj_short_default` | | |
| **6** | +1 solver: `quick_restart` | | | |
| **7** | +1 solver: `reduced_costs` | | | |
| **8** | +1 solver: `quick_restart_no_lp` | | | |
| **12** | +2 solvers: `lb_tree_search`, `pseudo_costs` | +2 solvers: `fj_long_default`, `fs_random` | | |
| **16** | +3 solvers: `objective_lb_search`, `objective_shaving_search_no_lp`, `probing` | +1 solver: `fs_random_quick_restart` | | |
| **20** | +2 solvers: `objective_shaving_search_max_lp`, `probing_max_lp` | +1 solver: `fj_short_lin_default` | | |
| **32** | +2 solvers: `objective_lb_search_max_lp`, `objective_lb_search_no_lp` | +8 solvers: `fj_long_lin_default`, `fj_long_lin_random`, `fj_long_random`, `fj_short_lin_random`, `fj_short_random`, `fs_random_no_lp`, `fs_random_quick_restart_no_lp` | +1 solver: `violation_ls(3)` | |
| **64** | | +11 solvers: `fj_long_default(2)`, `fj_long_lin_default(2)`, `fj_long_lin_random(2)`, `fj_long_random(2)`, `fj_short_default(2)`, `fj_short_lin_default(2)`, `fj_short_random(2)`, `fs_random(6)`, `fs_random_no_lp(6)`, `fs_random_quick_restart(6)`, `fs_random_quick_restart_no_lp(5)` | +1 solver: `violation_ls(7)` | |
Important steps:
- With a single worker, only the default subsolver is used.
- With two workers or more, CP-SAT starts using incomplete subsolvers, i.e.,
heuristics such as LNS.
- With five workers, CP-SAT will also have a first solution subsolver.
- With 32 workers, all 15 full problem subsolvers are used.
- For more than 32 workers, primarily the number of first solution subsolvers is
increased.
**Full problem subsolvers** are solvers that search the full problem space,
e.g., by a branch-and-bound algorithm. Available full problem subsolvers are:
- `default_lp`: LCG-based search with default linearization of the model.
- `max_lp`: Same as `default_lp` but with maximal linearization.
- `no_lp`: Same as `default_lp` but without linearization.
- `lb_tree_search`: This solver is focussed on improving the proven bound, not
on finding better solutions. By disproving the feasibility of the cheapest
nodes in the search tree, it incrementally improves the bound, but has only
little chances to find better solutions.
- `objective_lb_search`: Also focussed on improving the bound by disproving the
feasibility of the current lower bound.
- `objective_lb_search_max_lp`: With maximal linearization.
- `objective_lb_search_no_lp`: Without linearization.
- `objective_shaving_search_max_lp`: Should be quite similar to
`objective_lb_search_max_lp`.
- `objective_shaving_search_no_lp`: Should be quite similar to
`objective_lb_search_no_lp`.
- `probing`: Fixing variables and seeing what happens.
- `probing_max_lp`: Same as probing but with maximal linearization.
- `pseudo_costs`: Uses pseudo costs for branching, which are computed from
historical changes in objective bounds following certain branching decisions.
- `quick_restart`: Restarts the search more eagerly. Restarts rebuild the search
tree from scratch, but keep learned clauses. This allows to recover from bad
decisions, and lead to smaller search trees by learning from the mistakes of
the past.
- `quick_restart_no_lp`: Same as `quick_restart` but without linearization.
- `reduced_costs`: Uses the reduced costs of the linear relaxation for
branching.
- `core`: A strategy from the SAT-community that extracts unsatisfiable cores of
the formula.
- `fixed`: User-specified search strategy.
You can modify the used subsolvers by `solver.parameters.subsolvers`,
`solver.parameters.extra_subsolvers`, and `solver.parameters.ignore_subsolvers`.
This can be interesting, e.g., if you are using CP-SAT especially because the
linear relaxation is not useful (and the BnB-algorithm performing badly). There
are even more options, but for these you can simply look into the
[documentation](https://github.com/google/or-tools/blob/49b6301e1e1e231d654d79b6032e79809868a70e/ortools/sat/sat_parameters.proto#L513).
Be aware that fine-tuning such a solver is not a simple task, and often you do
more harm than good by tinkering around. However, I noticed that decreasing the
number of search workers can actually improve the runtime for some problems.
This indicates that at least selecting the right subsolvers that are best fitted
for your problem can be worth a shot. For example `max_lp` is probably a waste
of resources if you know that your model has a terrible linear relaxation. In
this context I want to recommend having a look on some relaxed solutions when
dealing with difficult problems to get a better understanding of which parts a
solver may struggle with (use a linear programming solver, like Gurobi, for
this).
You can evaluate the performance of the different strategies by looking at the
`Solutions` and `Objective bounds` blocks in the log. Here an example:
```
Solutions (7) Num Rank
'no_lp': 3 [1,7]
'quick_restart': 1 [3,3]
'quick_restart_no_lp': 3 [2,5]
Objective bounds Num
'initial_domain': 1
'objective_lb_search': 2
'objective_lb_search_no_lp': 4
'objective_shaving_search_no_lp': 1
```
For solutions, the first number is the number of solutions found by the
strategy, the second number is the range of the ranks of the solutions. The
value `[1,7]` indicates that the solutions found by the strategy have ranks
between 1 and 7. In this case, it means that the strategy `no_lp` found the best
and the worst solution.
For objective bounds, the number indicates how often the strategy contributed to
the best bound. For this example, it seems that the `no_lp` strategies are the
most successful. Note that for both cases, it is more interesting, which
strategies do not appear in the list.
In the search log, you can also see at which time which subsolver contributed
something. This log also includes the incomplete and first solution subsolvers.
```
#1 0.01s best:43 next:[6,42] no_lp (fixed_bools=0/155)
#Bound 0.01s best:43 next:[7,42] objective_shaving_search_no_lp (vars=73 csts=120)
#2 0.01s best:33 next:[7,32] quick_restart_no_lp (fixed_bools=0/143)
#3 0.01s best:31 next:[7,30] quick_restart (fixed_bools=0/123)
#4 0.01s best:17 next:[7,16] quick_restart_no_lp (fixed_bools=2/143)
#5 0.01s best:16 next:[7,15] quick_restart_no_lp (fixed_bools=22/147)
#Bound 0.01s best:16 next:[8,15] objective_lb_search_no_lp
#6 0.01s best:15 next:[8,14] no_lp (fixed_bools=41/164)
#7 0.01s best:14 next:[8,13] no_lp (fixed_bools=42/164)
#Bound 0.01s best:14 next:[9,13] objective_lb_search
#Bound 0.02s best:14 next:[10,13] objective_lb_search_no_lp
#Bound 0.04s best:14 next:[11,13] objective_lb_search_no_lp
#Bound 0.06s best:14 next:[12,13] objective_lb_search
#Bound 0.25s best:14 next:[13,13] objective_lb_search_no_lp
#Model 0.26s var:125/126 constraints:162/162
#Model 2.24s var:124/126 constraints:160/162
#Model 2.58s var:123/126 constraints:158/162
#Model 2.91s var:121/126 constraints:157/162
#Model 2.95s var:120/126 constraints:155/162
#Model 2.97s var:109/126 constraints:140/162
#Model 2.98s var:103/126 constraints:135/162
#Done 2.98s objective_lb_search_no_lp
#Done 2.98s quick_restart_no_lp
#Model 2.98s var:66/126 constraints:91/162
```
**Incomplete subsolvers** are solvers that do not search the full problem space,
but work heuristically. Notable strategies are large neighborhood search (LNS)
and feasibility pumps. The first one tries to find a better solution by changing
only a few variables, the second one tries to make infeasible/incomplete
solutions feasible. You can also run only the incomplete subsolvers by setting
`solver.parameters.use_lns_only = True`, but this needs to be combined with a
time limit, as the incomplete subsolvers do not know when to stop.
**First solution subsolvers** are strategies that try to find a first solution
as fast as possible. They are often used to warm up the solver and to get a
first impression of the problem.
If you are interested in how Gurobi parallelizes its search, you can find a
great video [here](https://www.youtube.com/watch?v=FJz1UxaMWRQ). Ed Rothberg
also explains the general opportunities and challenges of parallelizing a
solver, making it also interesting for understanding the parallelization of
CP-SAT.
> :warning: This section could need some help as there is the possibility that I
> am mixing up some of the strategies, or am drawing wrong connections.
#### Importing/Exporting Models for Comparison on Different Hardware
If you want to compare the performance of different parallelization levels or
different hardware, you can use the following code snippets to export a model.
Instead of having to rebuild the model or share any code, you can then simply
load the model on a different machine and run the solver.
```python
from ortools.sat.python import cp_model
from google.protobuf import text_format
from pathlib import Path
def _detect_binary_mode(filename: str) -> bool:
if filename.endswith((".txt", ".pbtxt", ".pb.txt")):
return False
if filename.endswith((".pb", ".bin", ".proto.bin", ".dat")):
return True
raise ValueError(f"Unknown extension for file: {filename}")
def export_model(model: cp_model.CpModel, filename: str, binary: bool | None = None):
binary = _detect_binary_mode(filename) if binary is None else binary
if binary:
Path(filename).write_bytes(model.Proto().SerializeToString())
else:
Path(filename).write_text(text_format.MessageToString(model.Proto()))
def import_model(filename: str, binary: bool | None = None) -> cp_model.CpModel:
binary = _detect_binary_mode(filename) if binary is None else binary
model = cp_model.CpModel()
if binary:
model.Proto().ParseFromString(Path(filename).read_bytes())
else:
text_format.Parse(Path(filename).read_text(), model.Proto())
return model
```
The binary mode is more efficient and should be used for large models. The text
mode is human-readable and can be easier shared and compared.
### Hints
If you have a good intuition about how the solution might look—perhaps from
solving a similar model or using a good heuristic—you can inform CP-SAT to
incorporate this knowledge into its search. Some workers will try to follow
these hints, which can significantly improve the solver's performance if they
are good. If the hints actually represent a feasible solution, the solver can
use them to prune the search space of all branches that have worse bounds than
the hints.
```python
model.add_hint(x, 1) # Suggest that x will probably be 1
model.add_hint(y, 2) # Suggest that y will probably be 2
```
For more examples, refer to
[the official example](https://github.com/google/or-tools/blob/stable/ortools/sat/samples/solution_hinting_sample_sat.py).
We will also see how to utilize hints for multi-objective optimization in the
[Coding Patterns](#06-coding-patterns) chapter.
> [!TIP]
>
> Hints can significantly improve solver performance, especially if it struggles
> to find a good initial solution (as indicated in the logs). This practice is
> often called **warm-starting** the solver. You do not need to provide values
> for all auxiliary variables, but if you use integer variables to approximate
> continuous variables, it is beneficial to provide hints for these. CP-SAT may
> struggle with quickly completing the solution, and only completed solutions
> can be used for pruning the search space. If CP-SAT needs a long time to
> complete the solution from the hint, it may have wasted a lot of time in
> branches it could otherwise have pruned.
To ensure your hints are correct, you can enable the following parameter, which
will make CP-SAT throw an error if the hints are incorrect:
```python
solver.parameters.debug_crash_on_bad_hint = True
```
If you suspect that your hints are not being utilized, it might indicate a
logical error in your model or a bug in your code. This parameter can help
diagnose such issues. However, this feature does not work reliably, so it should
not be solely relied upon.
> [!WARNING]
>
> In older versions of CP-SAT, hints could sometimes visibly slow down the
> solver, even if they were correct but not optimal. While this issue seems
> resolved in the latest versions, it is important to note that bad hints can
> still cause slowdowns by guiding the solver in the wrong direction.
Often, you may need to explore the impact of forcing certain variables to
specific values. To avoid copying the entire model multiple times to set the
values of variables explicitly, you can also use hints to fix variables their
hinted value with the following parameter:
```python
solver.parameters.fix_variables_to_their_hinted_value = True
```
Hints can be cleared afterwards by calling `model.clear_hints()`, allowing you
to test other hints without duplicating the model. While you cannot add complex
expressions directly, fixing variables enables you to experiment with more
intricate constraints without model duplication. For temporary complex
constraints, model copying using `model.CopyFrom` may still be necessary, along
with variable copying.
## Reinforcing the Model
For advanced users working with CP-SAT incrementally—i.e., modifying and solving
the model multiple times—the following parameter may be of interest:
```python
solver.parameters.fill_tightened_domains_in_response = True
```
When you remove the objective function and solve the feasibility version of your
model, the solver returns tightened domains for the variables. This can
significantly reduce the search space, improving solver performance, especially
when solving the model multiple times with different objectives or additional
constraints.
However, if the objective function is left in place, feasible solutions may be
excluded from the search space. These solutions might become relevant if the
objective or constraints are altered later.
Enabling this parameter does not modify the model itself; rather, it provides a
list of tightened variable domains in the response object which you can then use
in your model.
```python
# Example after solving the model
for i, v in enumerate(self.model.proto.variables):
print(f"Tightened domain for variable {i} '{v.name}' is {solver.response_proto.tightened_variables[i].domain}")
```
### Assumptions
Another way to explore the impact of forcing certain variables to specific
values is by means of assumptions, which is a common feature in many SAT
solvers. Unlike fixing hinted values, assumptions are restricted to boolean
literals in CP-SAT.
```python
b1 = model.new_bool_var("b1")
b2 = model.new_bool_var("b2")
b3 = model.new_bool_var("b3")
model.add_assumptions([b1, ~b2]) # assume b1=True, b2=False
model.add_assumption(b3) # assume b3=True (single literal)
# ... solve again and analyze ...
model.clear_assumptions() # clear all assumptions
```
> [!NOTE]
>
> While incremental SAT solvers can reuse learned clauses from previous runs
> despite changing assumptions, CP-SAT does not support this feature.
> Assumptions in CP-SAT only help avoid model duplication.
### Presolve
The CP-SAT solver includes a presolve step that simplifies the model before
solving it. This step can significantly reduce the search space and enhance
performance. However, presolve can be time-consuming, particularly for large
models. If your model is relatively simple—meaning there are few genuinely
challenging decisions for CP-SAT to make—and you notice that presolve is taking
a long time while the search itself is fast, you might consider reducing the
presolve effort.
For example, you can disable presolve entirely with:
```python
solver.parameters.cp_model_presolve = False
```
However, this approach might be too drastic, so you may prefer to limit presolve
rather than disabling it completely.
To reduce the number of presolve iterations, you can use:
```python
solver.parameters.max_presolve_iterations = 3
```
You can also limit specific presolve techniques. For instance, you can constrain
the time or intensity of probing, which is a technique that tries to fix
variables and observe the outcome. Although probing can be powerful, it is also
time-intensive.
```python
solver.parameters.cp_model_probing_level = 1
solver.parameters.presolve_probing_deterministic_time_limit = 5
```
There are additional parameters available to control presolve. Before making
adjustments, I recommend reviewing the solver log to identify which aspects of
presolve are causing long runtimes.
Keep in mind that reducing presolve increases the risk of failing to solve more
complex models. Ensure that you are not sacrificing performance on more
challenging instances just to speed up simpler cases.
### Adding Your Own Subsolver to the Portfolio
As we have seen, CP-SAT uses a portfolio of different subsolvers, each
configured with varying settings (e.g., different levels of linearization) to
solve the model. You can also define your own subsolver with a specific
configuration. It is important not to modify the parameters at the top level, as
this would affect all subsolvers, including the LNS-workers. Doing so could
disrupt the balance of the portfolio, potentially activating costly techniques
for the LNS-workers, which could slow them down to the point of being
ineffective. Additionally, you risk creating a default subsolver incompatible
with your model - such as one that requires an objective function - causing
CP-SAT to exclude most or all subsolvers from the portfolio, resulting in a
solver that is either inefficient or nonfunctional.
For example, in packing problems, certain expensive propagation techniques can
significantly speed up the search but can also drastically slow it down if
misused. To handle this, you can add a single subsolver that applies these
techniques. If the parameters do not help, only one worker will be slowed down,
while the rest of the portfolio remains unaffected. However, if the parameters
are beneficial, that worker can share its solutions and (variable) bounds with
the rest of the portfolio, boosting overall performance.
Here is how you can define and add a custom subsolver:
```python
from ortools.sat import sat_parameters_pb2
packing_subsolver = sat_parameters_pb2.SatParameters()
packing_subsolver.name = "MyPackingSubsolver"
packing_subsolver.use_area_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_energetic_reasoning_in_no_overlap_2d = True
packing_subsolver.use_timetabling_in_no_overlap_2d = True
packing_subsolver.max_pairs_pairwise_reasoning_in_no_overlap_2d = 5_000
# Add the subsolver to the portfolio
solver.parameters.subsolver_params.append(packing_subsolver) # Define the subsolver
solver.parameters.extra_subsolvers.append(
packing_subsolver.name
) # Activate the subsolver
```
After adding the subsolver, you can check the log to verify that it is included
in the list of active subsolvers. If it is not shown, you probably used
parameters incompatible with the model, causing the subsolver to be excluded.
```
8 full problem subsolvers: [MyPackingSubsolver, default_lp, max_lp, no_lp, probing, probing_max_lp, quick_restart, quick_restart_no_lp]
```
If you want to find out how the existing subsolvers are configured, you can
check out the
[cp_model_search.cc](https://github.com/google/or-tools/blob/stable/ortools/sat/cp_model_search.cc)
file in the OR-Tools repository.
> [!TIP]
>
> You can also overwrite the parameters of an existing subsolver by using the
> same name. Only the parameters you explicitly change will be updated, while
> the others will remain as they are. Additionally, you can add multiple
> subsolvers to the portfolio, but keep in mind that doing so might push some
> predefined subsolvers out of the portfolio if there are not enough workers
> available.
### Decision Strategy
In the end of this section, a more advanced parameter that looks interesting for
advanced users as it gives some insights into the search algorithm. It can be
useful in combination with `solver.parameters.enumerate_all_solutions = True` to
specify the order in which all solutions are iterated. It can also have some
impact on the search performance for normal optimization, but this is often hard
to predict, thus, you should leave the following parameters unless you have a
good reason to change them.
We can tell CP-SAT, how to branch (or make a decision) whenever it can no longer
deduce anything via propagation. For this, we need to provide a list of the
variables (order may be important for some strategies), define which variable
should be selected next (fixed variables are automatically skipped), and define
which value should be probed.
We have the following options for variable selection:
- `CHOOSE_FIRST`: the first not-fixed variable in the list.
- `CHOOSE_LOWEST_MIN`: the variable that could (potentially) take the lowest
value.
- `CHOOSE_HIGHEST_MAX`: the variable that could (potentially) take the highest
value.
- `CHOOSE_MIN_DOMAIN_SIZE`: the variable that has the fewest feasible
assignments.
- `CHOOSE_MAX_DOMAIN_SIZE`: the variable the has the most feasible assignments.
For the value/domain strategy, we have the options:
- `SELECT_MIN_VALUE`: try to assign the smallest value.
- `SELECT_MAX_VALUE`: try to assign the largest value.
- `SELECT_LOWER_HALF`: branch to the lower half.
- `SELECT_UPPER_HALF`: branch to the upper half.
- `SELECT_MEDIAN_VALUE`: try to assign the median value.
```python
model.add_decision_strategy([x], cp_model.CHOOSE_FIRST, cp_model.SELECT_MIN_VALUE)
# your can force CP-SAT to follow this strategy exactly
solver.parameters.search_branching = cp_model.FIXED_SEARCH
```
For example for [coloring](https://en.wikipedia.org/wiki/Graph_coloring) (with
integer representation of the color), we could order the variables by decreasing
neighborhood size (`CHOOSE_FIRST`) and then always try to assign the lowest
color (`SELECT_MIN_VALUE`). This strategy should perform an implicit
kernelization, because if we need at least $k$ colors, the vertices with less
than $k$ neighbors are trivial (and they would not be relevant for any
conflict). Thus, by putting them at the end of the list, CP-SAT will only
consider them once the vertices with higher degree could be colored without any
conflict (and then the vertices with lower degree will, too). Another strategy
may be to use `CHOOSE_LOWEST_MIN` to always select the vertex that has the
lowest color available. Whether this will actually help, has to be evaluated:
CP-SAT will probably notice by itself which vertices are the critical ones after
some conflicts.
> [!WARNING]
>
> I played around a little with selecting a manual search strategy. But even for
> the coloring, where this may even seem smart, it only gave an advantage for a
> bad model and after improving the model by symmetry breaking, it performed
> worse. Further, I assume that CP-SAT can learn the best strategy (Gurobi does
> such a thing, too) much better dynamically on its own.
---
## Understanding the CP-SAT Log
If you want to master CP-SAT, understanding the log is crucial. The log is the
output of the solver that shows you what the solver is doing and how it is
progressing.
The log consists of different parts. Let us go through them step by step.
> [!TIP]
>
> Use the [Log Analyzer](https://cpsat-log-analyzer.streamlit.app/) to get your
> own logs explained to you.
>
> [](https://cpsat-log-analyzer.streamlit.app/)
>
> [](https://github.com/d-krupke/CP-SAT-Log-Analyzer)
As a reminder, you activate logging with
```python
solver.parameters.log_search_progress = True # Enable logging
```
### Initialization
The log starts with the version of CP-SAT, the parameters you set, and how many
workers it has been using. For example, we have set a time limit via
`max_time_in_seconds` to 30 seconds. If you are given a log, you can directly
see under which conditions the solver was running.
```
Starting CP-SAT solver v9.10.4067
Parameters: max_time_in_seconds: 30 log_search_progress: true relative_gap_limit: 0.01
Setting number of workers to 16
```
### Initial Model Description
The next block provides an overview of the model before presolve, detailing the
number of variables and constraints, as well as their coefficients and domains.
```
Initial optimization model '': (model_fingerprint: 0x1d316fc2ae4c02b1)
#Variables: 450 (#bools: 276 #ints: 6 in objective)
- 342 Booleans in [0,1]
- 12 in [0][10][20][30][40][50][60][70][80][90][100]
- 6 in [0][10][20][30][40][100]
- 6 in [0][80][100]
- 6 in [0][100]
- 6 in [0,1][34][67][100]
- 12 in [0,6]
- 18 in [0,7]
- 6 in [0,35]
- 6 in [0,36]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kBoolOr: 30 (#literals: 72)
#kLinear1: 33 (#enforced: 12)
#kLinear2: 1'811
#kLinear3: 36
#kLinearN: 94 (#terms: 1'392)
```
For example, `- 12 in [22,57]` indicates that there are 12 variables with a
domain of `[22,57]`, meaning their values can range between 22 and 57.
Similarly, `#kLinearN: 94 (#terms: 1'392)` indicates the presence of 94 linear
constraints with 1,392 coefficients.
Comparing this data to the model after presolve (coming up soon) is useful to
ensure it aligns with your expectations. The presolve phase often reformulates
your model extensively to enhance efficiency.
Since most optimization models are created dynamically in code, reviewing this
section can help identify bugs or inefficiencies. Take the time to verify that
the numbers match your expectations and ensure you do not have too many or too
few variables or constraints of a certain type. This step is crucial as it also
provides insight into the number of auxiliary variables in your model, helping
you better understand its structure and complexity.
### Presolve Log
The next block represents the presolve phase, an essential component of CP-SAT.
During this phase, the solver reformulates your model for greater efficiency.
For instance, it may detect an affine relationship between variables, such as
`x=2y-1`, and replace `x` with `2y-1` in all constraints. It can also identify
and remove redundant constraints or unnecessary variables. For example, the log
entry `rule 'presolve: 33 unused variables removed.' was applied 1 time` may
indicate that some variables created by your code were unnecessary or became
redundant due to the reformulation. Multiple rounds of applying various rules
for domain reduction, expansion, equivalence checking, substitution, and probing
are performed during presolve. These rules can significantly enhance the
efficiency of your model, though they may take some time to run. However, this
time investment usually pays off during the search phase.
```
Starting presolve at 0.00s
3.26e-04s 0.00e+00d [DetectDominanceRelations]
6.60e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=4 #num_dual_strengthening=3
2.69e-05s 0.00e+00d [ExtractEncodingFromLinear] #potential_supersets=44 #potential_subsets=12
[Symmetry] Graph for symmetry has 2'224 nodes and 5'046 arcs.
[Symmetry] Symmetry computation done. time: 0.000374304 dtime: 0.00068988
[Symmetry] #generators: 2, average support size: 12
[Symmetry] 12 orbits with sizes: 2,2,2,2,2,2,2,2,2,2,...
[Symmetry] Found orbitope of size 6 x 2
[SAT presolve] num removable Booleans: 0 / 309
[SAT presolve] num trivial clauses: 0
[SAT presolve] [0s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [3.0778e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
[SAT presolve] [4.6758e-05s] clauses:570 literals:1152 vars:303 one_side_vars:268 simple_definition:35 singleton_clauses:0
1.10e-02s 9.68e-03d [Probe] #probed=1'738 #new_bounds=12 #new_binary_clauses=1'111
2.34e-03s 0.00e+00d [MaxClique] Merged 602(1374 literals) into 506(1960 literals) at_most_ones.
3.31e-04s 0.00e+00d [DetectDominanceRelations]
1.89e-03s 0.00e+00d [PresolveToFixPoint] #num_loops=2 #num_dual_strengthening=1
5.45e-04s 0.00e+00d [ProcessAtMostOneAndLinear]
8.19e-04s 0.00e+00d [DetectDuplicateConstraints] #without_enforcements=306
8.62e-05s 7.21e-06d [DetectDominatedLinearConstraints] #relevant_constraints=114 #num_inclusions=42
...
Presolve summary:
- 54 affine relations were detected.
- rule 'TODO dual: make linear1 equiv' was applied 6 times.
- rule 'TODO dual: only one blocking constraint?' was applied 1'074 times.
- rule 'TODO dual: only one unspecified blocking constraint?' was applied 48 times.
- rule 'TODO duplicate: identical constraint with different enforcements' was applied 612 times.
- rule 'TODO linear2: contains a Boolean.' was applied 1'626 times.
- rule 'TODO symmetry: add symmetry breaking inequalities?' was applied 2 times.
...
- rule 'objective: variable not used elsewhere' was applied 15 times.
- rule 'presolve: 33 unused variables removed.' was applied 1 time.
- rule 'presolve: iteration' was applied 2 times.
- rule 'variables with 2 values: create encoding literal' was applied 12 times.
- rule 'variables with 2 values: new affine relation' was applied 12 times.
- rule 'variables: canonicalize affine domain' was applied 30 times.
- rule 'variables: detect half reified value encoding' was applied 54 times.
```
The presolve log can be challenging to read, but it provides vital information
on the simplifications and optimizations made by CP-SAT. Reviewing this log can
help you understand the transformations applied to your model, allowing you to
identify and address any unnecessary variables or constraints in your code.
### Presolved Model
This is the most important block of the presolve phase and gives an overview of
the model after presolve. It contains the number of variables and constraints,
as well as coefficients and domains.
`- 200 in [0,199]` will indicate that there are 200 variables with domain
`[0,199]`, i.e., values between 0 and 199. `- 6 in [0,1][34][67][100]` will
indicate that there are 6 variables with domain `[0,1][34][67][100]`, i.e.,
values 0, 1, 34, 67, and 100. `#kLinearN: 3'000 (#terms: 980'948)` indicates
that there are 3000 linear constraints with 980'948 coefficients.
It is useful to compare this to the initial model, to see if your model was
simplified by presolve, which indicates that you can simplify your model
yourself, saving presolve time. If you notice that a lot of time is spent in
presolve but it does not simplify your model, you can try to disable/reduce
presolve.
It is also interesting to see if the presolve replaced some of your constraints
with more efficient ones.
```
Presolved optimization model '': (model_fingerprint: 0xb4e599720afb8c14)
#Variables: 405 (#bools: 261 #ints: 6 in objective)
- 309 Booleans in [0,1]
- 12 in [0][2,6]
- 6 in [0][4,5]
- 6 in [0,3]
- 6 in [0,4]
- 6 in [0,6]
- 6 in [0,7]
- 12 in [0,10]
- 12 in [0,13]
- 6 in [0,100]
- 12 in [21,57]
- 12 in [22,57]
#kAtMostOne: 452 (#literals: 1'750)
#kBoolAnd: 36 (#enforced: 36) (#literals: 90)
#kBoolOr: 12 (#literals: 36)
#kLinear1: 854 (#enforced: 854)
#kLinear2: 42
#kLinear3: 24
#kLinearN: 48 (#enforced: 18) (#terms: 1'046)
```
> [!NOTE]
>
> This is the same model as in the initial model description. Take some time to
> compare the two and see how much the presolve-phase has reformulated the
> model.
### Preloading Model
This block serves as a prelude to the search phase and provides an overview of
the model at the beginning of the search. Typically, this information is not
very interesting unless the presolve phase was highly effective, essentially
solving the model before the search phase begins. This can lead to entries that
look very similar to that of the actual search phase, which comes next.
```
Preloading model.
#Bound 0.05s best:-inf next:[-0.7125] initial_domain
[Symmetry] Graph for symmetry has 2,111 nodes and 5,096 arcs.
[Symmetry] Symmetry computation done. time: 0.000365377 dtime: 0.00068122
[Symmetry] #generators: 2, average support size: 12
[Symmetry] Found orbitope of size 6 x 2
#Model 0.05s var:405/405 constraints:1468/1468
```
### Search Phase
The search progress log is an essential element of the overall log, crucial for
identifying performance bottlenecks. It clearly demonstrates the solver's
progression over time and pinpoints where it faces significant challenges. It is
important to discern whether the upper or lower bounds are causing issues, or if
the solver initially finds a near-optimal solution but struggles to minimize a
small remaining gap.
> [!WARNING]
>
> For models without an objective, especially the log of the search phase will
> look very different. This chapter focuses on models with an objective.
The structure of the log entries is standardized as follows:
```
EVENT NAME | TIME | BEST SOLUTION | RANGE OF THE SEARCH | COMMENT
```
For instance, an event marked `#2` indicates the discovery of the second
solution. Here, you will observe an improvement in the `BEST SOLUTION` metric. A
notation like `best:16` confirms that the solver has found a solution with a
value of 16.
An event with `#Bound` denotes an enhancement in the bound, as seen by a
reduction in the `RANGE OF THE SEARCH`. A detail such as `next:[7,14]` signifies
that the solver is now focused on finding a solution valued between 7 and 14.
The `COMMENT` section provides essential information about the strategies that
led to these improvements.
Events labeled `#Model` signal modifications to the model, such as fixing
certain variables.
```
Starting search at 0.05s with 16 workers.
11 full problem subsolvers: [core, default_lp, lb_tree_search, max_lp, no_lp, objective_lb_search, probing, pseudo_costs, quick_restart, quick_restart_no_lp, reduced_costs]
4 first solution subsolvers: [fj_long_default, fj_short_default, fs_random, fs_random_quick_restart]
9 incomplete subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, rins/rens, rnd_cst_lns, rnd_var_lns, violation_ls]
3 helper subsolvers: [neighborhood_helper, synchronization_agent, update_gap_integral]
#1 0.06s best:-0 next:[1,7125] fj_short_default(batch:1 #lin_moves:0 #lin_evals:0 #weight_updates:0)
#2 0.07s best:1050 next:[1051,7125] fj_long_default(batch:1 #lin_moves:1'471 #lin_evals:2'102 #weight_updates:123)
#3 0.08s best:1051 next:[1052,7125] quick_restart_no_lp (fixed_bools=0/884)
#Bound 0.09s best:1051 next:[1052,1650] default_lp
#4 0.10s best:1052 next:[1053,1650] quick_restart_no_lp (fixed_bools=22/898)
#5 0.10s best:1053 next:[1054,1650] quick_restart_no_lp (fixed_bools=22/901)
#6 0.11s best:1055 next:[1056,1650] quick_restart_no_lp (fixed_bools=22/906)
#7 0.11s best:1056 next:[1057,1650] quick_restart_no_lp (fixed_bools=22/909)
#8 0.11s best:1057 next:[1058,1650] quick_restart_no_lp (fixed_bools=22/913)
#9 0.11s best:1058 next:[1059,1650] quick_restart_no_lp (fixed_bools=22/914)
#10 0.12s best:1059 next:[1060,1650] quick_restart_no_lp (fixed_bools=26/916)
#11 0.12s best:1060 next:[1061,1650] quick_restart_no_lp (fixed_bools=26/917)
#12 0.12s best:1061 next:[1062,1650] quick_restart_no_lp (fixed_bools=26/918)
#13 0.13s best:1062 next:[1063,1650] quick_restart_no_lp (fixed_bools=28/918)
#14 0.13s best:1063 next:[1064,1650] quick_restart_no_lp (fixed_bools=28/921)
#Bound 0.13s best:1063 next:[1064,1579] lb_tree_search
#15 0.13s best:1064 next:[1065,1579] quick_restart_no_lp (fixed_bools=28/924)
#Model 0.13s var:404/405 constraints:1435/1468
#16 0.13s best:1065 next:[1066,1579] quick_restart_no_lp (fixed_bools=28/930)
#17 0.13s best:1066 next:[1067,1579] quick_restart_no_lp (fixed_bools=28/932)
#18 0.14s best:1067 next:[1068,1579] quick_restart_no_lp (fixed_bools=28/935)
#19 0.14s best:1071 next:[1072,1579] quick_restart_no_lp (fixed_bools=28/946)
#20 0.15s best:1072 next:[1073,1579] quick_restart_no_lp (fixed_bools=28/950)
#21 0.15s best:1089 next:[1090,1579] quick_restart_no_lp (fixed_bools=28/966)
#22 0.15s best:1090 next:[1091,1579] quick_restart_no_lp (fixed_bools=28/966)
...
#Bound 8.73s best:1449 next:[1450,1528] lb_tree_search (nodes=13/18 rc=0 decisions=133 @root=28 restarts=0)
#Model 8.99s var:390/405 constraints:1292/1468
#Bound 9.37s best:1449 next:[1450,1527] lb_tree_search (nodes=15/20 rc=0 decisions=152 @root=28 restarts=0)
#Bound 11.79s best:1449 next:[1450,1526] lb_tree_search (nodes=78/83 rc=0 decisions=327 @root=28 restarts=0)
#Bound 12.40s best:1449 next:[1450,1525] lb_tree_search (nodes=96/104 rc=0 decisions=445 @root=28 restarts=0)
#Bound 13.50s best:1449 next:[1450,1524] lb_tree_search (nodes=123/138 rc=0 decisions=624 @root=28 restarts=0)
#Bound 15.71s best:1449 next:[1450,1523] lb_tree_search (nodes=164/180 rc=0 decisions=847 @root=29 restarts=0)
#132 16.69s best:1450 next:[1451,1523] rnd_var_lns (d=0.88 s=657 t=0.10 p=0.54 stall=53 h=folio_rnd)
#Bound 17.13s best:1450 next:[1451,1522] lb_tree_search (nodes=176/192 rc=0 decisions=1001 @root=30 restarts=0)
#Model 17.85s var:389/405 constraints:1289/1468
#Bound 19.35s best:1450 next:[1451,1521] lb_tree_search (nodes=44/44 rc=0 decisions=1112 @root=33 restarts=1)
#Bound 20.12s best:1450 next:[1451,1520] lb_tree_search (nodes=53/53 rc=0 decisions=1176 @root=34 restarts=1)
#Bound 22.08s best:1450 next:[1451,1519] lb_tree_search (nodes=114/114 rc=0 decisions=1369 @root=35 restarts=1)
#Bound 23.92s best:1450 next:[1451,1518] lb_tree_search (nodes=131/131 rc=0 decisions=1517 @root=36 restarts=1)
#Bound 25.84s best:1450 next:[1451,1517] lb_tree_search (nodes=174/174 rc=0 decisions=1754 @root=36 restarts=1)
#Bound 29.35s best:1450 next:[1451,1515] objective_lb_search
```
As this log is event-driven, it can be challenging to interpret. The
[Log Analyzer](https://cpsat-log-analyzer.streamlit.app/) helps by automatically
plotting these values in a more understandable way. Since the values at the
beginning of the search are often out of scale, use the zoom function to focus
on the relevant parts of the search.
| 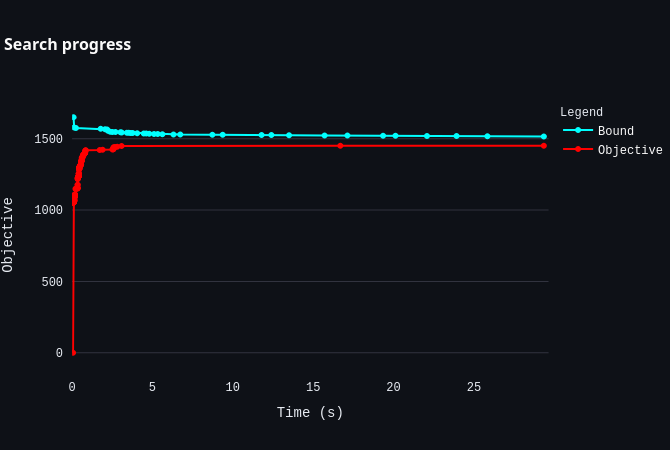 | 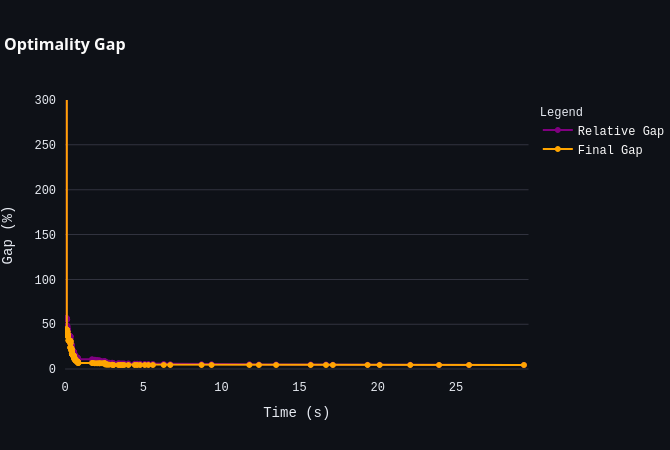 |  |
| :----------------------------------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------------------------: |
| Shows how the lower and upper bounds change over time. | Shows how quickly the optimality gap converges. | Shows how the model changes over time as new insights from the search allow the solver to fix variables. |
### Subsolver Details
Now there comes a lot of information about the different subsolvers that are
used. This is a very detailed part of the log and can be overwhelming. You
already need to be rather deep into the details of CP-SAT to actually make any
use of this information. It is primarily intended for the developers of CP-SAT.
It gives you insights into how the various subsolvers have been contributing to
the solution, how the otherwise hidden LP-techniques, including cutting planes,
have been used, and how the different heuristics have been applied. Based on
this data, you could try to tune the various parameters of CP-SAT for your
problem. However, note that you will probably need a lot of experience and
experiments to gain an advantage compared to the default settings.
```
Task timing n [ min, max] avg dev time n [ min, max] avg dev dtime
'core': 1 [ 29.95s, 29.95s] 29.95s 0.00ns 29.95s 1 [ 27.99s, 27.99s] 27.99s 0.00ns 27.99s
'default_lp': 1 [ 29.94s, 29.94s] 29.94s 0.00ns 29.94s 1 [ 21.11s, 21.11s] 21.11s 0.00ns 21.11s
'feasibility_pump': 123 [ 4.51ms, 70.61ms] 38.93ms 9.87ms 4.79s 122 [ 6.31ms, 41.77ms] 17.96ms 6.53ms 2.19s
'fj_long_default': 1 [ 10.28ms, 10.28ms] 10.28ms 0.00ns 10.28ms 1 [ 2.08ms, 2.08ms] 2.08ms 0.00ns 2.08ms
'fj_short_default': 1 [579.83us, 579.83us] 579.83us 0.00ns 579.83us 0 [ 0.00ns, 0.00ns] 0.00ns 0.00ns 0.00ns
'fs_random': 1 [ 6.57ms, 6.57ms] 6.57ms 0.00ns 6.57ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'fs_random_quick_restart': 1 [ 6.82ms, 6.82ms] 6.82ms 0.00ns 6.82ms 1 [ 20.00ns, 20.00ns] 20.00ns 0.00ns 20.00ns
'graph_arc_lns': 123 [ 3.65ms, 430.55ms] 169.44ms 106.16ms 20.84s 123 [ 10.00ns, 119.31ms] 61.95ms 43.70ms 7.62s
...
Clauses shared Num
'core': 137
'default_lp': 1
'lb_tree_search': 4
'max_lp': 1
'no_lp': 10
'objective_lb_search': 3
'pseudo_costs': 4
'quick_restart': 4
'quick_restart_no_lp': 74
'reduced_costs': 2
```
### Summary
This final block of the log contains a summary by the solver. Here you find the
most important information, such as how successful the search was.
You can find the original documentation
[here](https://github.com/google/or-tools/blob/8768ed7a43f8899848effb71295a790f3ecbe2f2/ortools/sat/cp_model.proto#L720).
```
CpSolverResponse summary:
status: FEASIBLE # The status of the search. Can be FEASIBLE, OPTIMAL, INFEASIBLE, UNKNOWN, or MODEL_INVALID.
objective: 1450 # The value of the objective function for the best solution found.
best_bound: 1515 # The proven bound on the objective function, i.e., the best possible value.
integers: 416
booleans: 857
conflicts: 0
branches: 370
propagations: 13193
integer_propagations: 6897
restarts: 370
lp_iterations: 0
walltime: 30.4515 # The time in seconds since solver creation.
usertime: 30.4515
deterministic_time: 306.548
gap_integral: 1292.47 # The integral of the gap over time. A lower value will indicate that the solver is converging faster.
solution_fingerprint: 0xf10c47f1901c2c16 # Useful to check if two runs result in the same solution.
```
## How does it work?
CP-SAT is a versatile _portfolio_ solver, centered around a _Lazy Clause
Generation (LCG)_ based Constraint Programming Solver, although it encompasses a
broader spectrum of technologies.
In its role as a portfolio solver, CP-SAT concurrently executes a multitude of
diverse algorithms and strategies, each possessing unique strengths and
weaknesses. These elements operate largely independently but engage in
information exchange, sharing progress when better solutions emerge or tighter
bounds become available.
While this may initially appear as an inefficient approach due to potential
redundancy, it proves highly effective in practice. The rationale behind this
lies in the inherent challenge of predicting which algorithm is best suited to
solve a given problem (No Free Lunch Theorem). Thus, the pragmatic strategy
involves running various approaches in parallel, with the hope that one will
effectively address the problem at hand. Note that you can also specify which
algorithms should be used if you already know which strategies are promising or
futile.
In contrast, Branch and Cut-based Mixed Integer Programming solvers like Gurobi
implement a more efficient partitioning of the search space to reduce
redundancy. However, they specialize in a particular strategy, which may not
always be the optimal choice, although it frequently proves to be so.
CP-SAT employs Branch and Cut techniques, including linear relaxations and
cutting planes, as part of its toolkit. Models that can be efficiently addressed
by a Mixed Integer Programming (MIP) solver are typically a good match for
CP-SAT as well. Nevertheless, CP-SAT's central focus is the implementation of
Lazy Clause Generation, harnessing SAT-solvers rather than relying primarily on
linear relaxations. As a result, CP-SAT may exhibit somewhat reduced performance
when confronted with MIP problems compared to dedicated MIP solvers. However, it
gains a distinct advantage when dealing with problems laden with intricate
logical constraints.
The concept behind Lazy Clause Generation involves the (incremental)
transformation of the problem into a SAT-formula, subsequently employing a
SAT-solver to seek a solution (or prove bounds by infeasibility). To mitigate
the impracticality of a straightforward conversion, Lazy Clause Generation
leverages an abundance of lazy variables and clauses.
Notably, the
[Cook-Levin Theorem](https://en.wikipedia.org/wiki/Cook%E2%80%93Levin_theorem)
attests that any problem within the realm of NP can be translated into a
SAT-formula. Optimization, in theory, could be achieved through a simple binary
search. However, this approach, while theoretically sound, lacks efficiency.
CP-SAT employs a more refined encoding scheme to tackle optimization problems
more effectively.
If you want to understand the inner workings of CP-SAT, you can follow the
following learning path:
1. Learn how to get a feasible solution based on boolean logics with
SAT-solvers: Backtracking, DPLL, CDCL, VSIDS, ...
- [Historical Overview by Armin Biere](https://youtu.be/DU44Y9Pt504) (video)
- [Donald Knuth - The Art of Computer Programming, Volume 4, Fascicle 6: Satisfiability](https://www-cs-faculty.stanford.edu/~knuth/taocp.html)
(book)
- [Carsten Sinz and Tomas Baylo - Practical SAT Solving](https://baldur.iti.kit.edu/sat/#about)
(slides)
2. Learn how to get provably optimal solutions via classical Mixed Integer
Programming:
- Linear Programming: Simplex, Duality, Dual Simplex, ...
- [Understanding and Using Linear Programming](https://link.springer.com/book/10.1007/978-3-540-30717-4)
(book)
- [Optimization in Operations Research by Ronald Rardin](https://www.pearson.com/en-us/subject-catalog/p/optimization-in-operations-research/P200000003508/9780137982066)
(very long book also containing Mixed Integer Programming, Heuristics,
and advanced topics. For those who want to dive deep.)
- [Video Series by Gurobi](https://www.youtube.com/playlist?list=PLHiHZENG6W8BeAfJfZ3myo5dsSQjEV5pJ)
- Mixed Integer Programming: Branch and Bound, Cutting Planes, Branch and
Cut, ...
- [Discrete Optimization on Coursera with Pascal Van Hentenryck and Carleton Coffrin](https://www.coursera.org/learn/discrete-optimization)
(video course, including also Constraint Programming and Heuristics)
- [Gurobi Resources](https://www.gurobi.com/resource/mip-basics/) (website)
3. Learn the additional concepts of LCG Constraint Programming: Propagation,
Lazy Clause Generation, ...
- [Combinatorial Optimisation and Constraint Programming by Prof. Pierre Flener at Uppsala University in Sweden](https://user.it.uu.se/~pierref/courses/COCP/slides/)
(slides)
- [Talk by Peter Stuckey](https://www.youtube.com/watch?v=lxiCHRFNgno)
(video)
- [Paper on Lazy Clause Generation](https://people.eng.unimelb.edu.au/pstuckey/papers/cp09-lc.pdf)
(paper)
4. Learn the details of CP-SAT:
- [The proto-file of the parameters](https://github.com/google/or-tools/blob/stable/ortools/sat/sat_parameters.proto)
(source)
- [The complete source code](https://github.com/google/or-tools/tree/stable/ortools/sat)
(source)
- [A recent talk by the developers of CP-SAT](https://www.youtube.com/live/vvUxusrUcpU?si=qVsXMq0xSOsfghTM)
(video)
- [Another recent talk by the developers of CP-SAT](http://egon.cheme.cmu.edu/ewo/video/CP_SAT_LP_google.mp4)
(video)
- [A talk by the developers of CP-SAT](https://youtu.be/lmy1ddn4cyw) (video)
If you already have a background in Mixed Integer Programming, you may directly
jump into the slides of
[Combinatorial Optimisation and Constraint Programming](https://user.it.uu.se/~pierref/courses/COCP/slides/).
This is a full and detailed course on constraint programming, and will probably
take you some time to work through. However, it gives you all the knowledge you
need to understand the constraint programming part of CP-SAT.
> Originally, I wrote a short introduction into each of the topics, but I
> decided to remove them as the material I linked to is much better than what I
> could have written. You can find a backup of the old version
> [here](https://github.com/d-krupke/cpsat-primer/blob/main/old_how_does_it_work.md).
### What Happens in CP-SAT During Solve?
What exactly happens when you run `solver.solve(model)`?
1. **Model Loading and Verification:**
- The model is read from its protobuf representation.
- The model is verified for correctness.
2. **Preprocessing (multiple iterations, controlled by
`max_presolve_iterations`):**
1. **Presolve (domain reduction):**
- This step reduces the problem size by simplifying variable domains. For
more on this, check out:
- [Video on SAT preprocessing](https://www.youtube.com/watch?v=ez9ArInp8w4)
- [Video on MaxSAT preprocessing](https://www.youtube.com/watch?v=xLg4hbM8ooM)
- [Paper on MIP presolving](https://opus4.kobv.de/opus4-zib/frontdoor/index/index/docId/6037)
2. **Expansion of higher-level constraints:**
- Higher-level constraints are expanded into lower-level constraints,
CP-SAT actually can propagate efficiently, but which are less
comfortable for you to write. See
[FlatZinc and Flattening](https://www.minizinc.org/doc-2.5.5/en/flattening.html)
for a similar process.
3. **Detection of equivalent variables and affine relations:**
- Affine relations, such as `a * x + b = y`, are identified. Read more
about
[affine relations here](https://personal.math.ubc.ca/~cass/courses/m309-03a/a1/olafson/affine_fuctions.htm).
4. **Substitution with canonical representations:**
- Detected affine relations are replaced with canonical representations.
5. **Variable probing:**
- Some variables are tested to determine if they can be fixed or if
further equivalences can be identified.
3. **Loading and Relaxation:**
- The preprocessed model is loaded into the underlying solver, and linear
relaxations are created.
4. **Solution Search:**
- The solver searches for solutions and bounds until the lower and upper
bounds converge or another stopping criterion is met (e.g., time limit).
- Several full subsolvers, each using a unique strategy, are run across
different threads. These strategies may include:
- More linearized models
- Aggressive restarts
- Focus on either the lower or upper bound
- Each subsolver can theoretically find the optimal solution, but some are
faster than others.
5. **First Solution Search and Local Search:**
- Additional "first solution searchers" are launched on remaining threads.
These stop once a feasible solution is found.
- Once a feasible solution is discovered, incomplete subsolvers take over,
applying local search heuristics such as Large Neighborhood Search (LNS).
These subsolvers attempt to improve the solution by iterating through
various strategies via a Round Robin approach.
- During each LNS iteration:
1. A copy of the model is made, and a solution is selected from the pool of
solutions.
2. A subset of variables is removed from the solution (the method for
choosing this subset varies between strategies). The neighborhood of
these variables is then explored for a better solution.
3. The remaining variables are fixed to their current values in the copied
model.
4. The simplified model is presolved with the fixed variables, which often
makes the model much easier to solve.
5. The simplified model is then solved using a complete strategy, but with
a short time limit and on a single thread.
6. If a new solution is found, it’s added to the pool of solutions.
6. **Solution Transformation:**
- The final solution is transformed back into the original model format,
allowing you to query the values of the variables as defined in your
original model.
This is taken from [this talk](https://youtu.be/lmy1ddn4cyw?t=434) and slightly
extended.
### The use of linear programming techniques
As already mentioned before, CP-SAT also utilizes the (dual) simplex algorithm
and linear relaxations. The linear relaxation is implemented as a propagator and
potentially executed at every node in the search tree but only at lowest
priority. A significant difference to the application of linear relaxations in
branch and bound algorithms is that only some pivot iterations are performed (to
make it faster). However, as there are likely much deeper search trees and the
warm-starts are utilized, the optimal linear relaxation may still be computed,
just deeper down the tree (note that for SAT-solving, the search tree is usually
traversed DFS). At root level, even cutting planes such as Gomory-Cuts are
applied to improve the linear relaxation.
The linear relaxation is used for detecting infeasibility (IPs can actually be
more powerful than simple SAT, at least in theory), finding better bounds for
the objective and variables, and also for making branching decisions (using the
linear relaxation's objective and the reduced costs).
The used Relaxation Induced Neighborhood Search RINS (LNS worker), a very
successful heuristic, of course also uses linear programming.
### Limitations of CP-SAT
While CP-SAT is undeniably a potent solver, it does possess certain limitations
when juxtaposed with alternative techniques:
1. While proficient, it may not match the speed of a dedicated SAT-solver when
tasked with solving SAT-formulas, although its performance remains quite
commendable.
2. Similarly, for classical MIP-problems, CP-SAT may not outpace dedicated
MIP-solvers in terms of speed, although it still delivers respectable
performance.
3. Unlike MIP/LP-solvers, CP-SAT lacks support for continuous variables, and the
workarounds to incorporate them may not always be highly efficient. In cases
where your problem predominantly features continuous variables and linear
constraints, opting for an LP-solver is likely to yield significantly
improved performance.
4. CP-SAT does not offer support for lazy constraints or iterative model
building, a feature available in MIP/LP-solvers and select SAT-solvers.
Consequently, the application of exponential-sized models, which are common
and pivotal in Mixed Integer Programming, may be restricted.
5. CP-SAT is limited to the Simplex algorithm and does not feature interior
point methods. This limitation prevents it from employing polynomial time
algorithms for certain classes of quadratic constraints, such as Second Order
Cone constraints. In contrast, solvers like Gurobi utilize the Barrier
algorithm to efficiently tackle these constraints in polynomial time.
CP-SAT might also exhibit inefficiency when confronted with certain constraints,
such as modulo constraints. However, it's noteworthy that I am not aware of any
alternative solver capable of efficiently addressing these specific constraints.
At times, NP-hard problems inherently pose formidable challenges, leaving us
with no alternative but to seek more manageable modeling approaches instead of
looking for better solvers.
## Alternatives: CP-SAT's Place in the World of Optimization
When you begin exploring optimization, you will encounter a plethora of tools,
techniques, and communities. It can be overwhelming, as these groups, while
sharing many similarities, also differ significantly. They might use the same
terminology for different concepts or different terms for the same concepts,
adding to the confusion. Not too many experts can effectively navigate these
varied communities and techniques. Often, even specialists, including
professors, concentrate on a singular technique or community, remaining unaware
of potentially more efficient methods developed in other circles.
If you are interested in understanding the connections between different
optimization concepts, consider watching the talk
[Logic, Optimization, and Constraint Programming: A Fruitful Collaboration](https://simons.berkeley.edu/talks/john-hooker-carnegie-mellon-university-2023-04-19)
by John Hooker. Please note that this is an academic presentation and assumes
some familiarity with theoretical computer science.
Let us now explore the various tools and techniques available, and see how they
compare to CP-SAT. Please note that this overview is high-level and not
exhaustive. If you have any significant additions, feel free to open an issue,
and I will consider including them.
- **Mixed Integer (Linear) Programming (MIP):** MIP is a highly effective method
for solving a variety of optimization problems, particularly those involving
networks like flow or tour problems. While MIP only supports linear
constraints, making it less expressive than CP-SAT, it is often the best
choice if your model is compatible with these constraints. CP-SAT incorporates
techniques from MIP, but with limitations, including the absence of continuous
variables and incremental modeling. Consequently, pure MIP-solvers, being more
specialized, tend to offer greater efficiency for certain applications.
Notable MIP-solvers include:
- [Gurobi](https://www.gurobi.com/): A commercial solver known for its
state-of-the-art capabilities in MIP-solving. It offers free academic
licenses, exceptional performance, user-friendliness, and comprehensive
support through documentation and expert-led webinars. Gurobi is
particularly impressive in handling complex, large-scale problems.
- [SCIP](https://www.scipopt.org/): An open-source solver that provides a
Python interface. Although not as efficient or user-friendly as Gurobi, SCIP
allows extensive customization and is ideal for research and development,
especially for experts needing to implement advanced decomposition
techniques. If you know how to use it, you can achieve better performance
than any other solver for certain problems (especially with Branch and
Price).
- [FICO Xpress Optimization](https://www.fico.com/en/products/fico-xpress-optimization):
Another popular commercial solver. A lot of the SCIP developers seem to end
up either at Gurobi or Xpress.
- [COPT Cardinal Solver](https://www.copt.de/): A relatively new commercial
solver that seems to be very strong for some problem classes.
- [HiGHS](https://highs.dev/): A newer solver licensed under MIT, presenting
an interesting alternative to SCIP. It is possibly faster and features a
more user-friendly interface, but is less versatile. For performance
benchmarks, see [here](https://plato.asu.edu/ftp/milp.html).
- **Constraint Programming (CP):** Constraint Programming is a more general
approach to optimization problems than MIP. As the name suggests, it focuses
on constraints and solvers usually come with a lot of advanced constraints
that can be used to describe your problem more naturally. A classical example
is the `AllDifferent`-constraint, which is very hard to model in MIP, but
would allow, e.g., to trivially model a Sudoku problem. Constraint Programming
has been very successful for example in solving scheduling problems, where you
have a lot of constraints that are hard to model with linear constraints. The
internal techniques of CP-solvers are often more logic-based and less linear
algebra-based than MIP-solvers. Popular CP-solvers are:
- [OR-Tools' CP-SAT](https://github.com/google/or-tools/): Discussed in this
primer, CP-SAT combines various optimization techniques, including those
from MIP solvers, but its primary technique is Lazy Clause Generation. This
approach translates problems into (Max-)SAT formulas for resolution.
- [Choco](https://choco-solver.org/): A traditional CP solver developed in
Java, licensed under the BSD 4-Clause. While it may not match CP-SAT in
efficiency or modernity, Choco offers significant flexibility, including the
option to integrate custom propagators.
- **SAT-Solvers:** If your problem is actually just to find a feasible solution
for some boolean variables, you may want to use a SAT-solver. SAT-solvers are
surprisingly efficient and can often handle problems with millions of
variables. If you are clever, you can also do some optimization problems with
SAT-solvers, as CP-SAT actually does. Most SAT-solvers support incremental
modelling, and some support cardinality constraints. However, they are pretty
low-level and CP-SAT actually can achieve similar performance for many
problems. A popular library for SAT-solvers is:
- [PySAT](https://pysathq.github.io/): PySAT is a Python library under MIT
license that provides a nice interface to many SAT-solvers. It is very easy
to use and allows you to switch between different solvers without changing
your code. It is a good choice if you want to experiment with SAT-solvers.
- There are many solvers popping up every year and many of them are open
source. Check out the [SAT Competition](http://www.satcompetition.org/) to
see the current state of the art. Most of the solvers are written in C or
C++ and do not provide much documentation. However, as SAT-formulas are very
simple and the solvers usually do not have complex dependencies, they can
still be reasonably easy to use.
- **Satisfiability modulo theories (SMT):** SMT-solvers represent an advanced
tier above traditional SAT-solvers. They aim to check the satisfiability of
mathematical formulas by extending propositional logic with additional
theories like linear arithmetic, bit-vectors, arrays, and quantifiers. For
instance, an SMT-solver can determine if a formula is satisfiable under
conditions where all variables are integers that meet specific linear
constraints. Similar to the Lazy Clause Generation utilized by CP-SAT,
SMT-solvers usually use a SAT-solver in the backend, extended by complex
encodings and additional propagators to handle an extensive portfolio of
expressions. These solvers are commonly used in automated theorem proving and
system verification. A popular SMT-solver is:
- [Z3](https://github.com/z3prover/z3): Developed by Microsoft and available
under the MIT license, Z3 offers a robust Python interface and comprehensive
documentation, making it accessible for a variety of applications.
- **Nonlinear Programming (NLP):** Many MIP-solvers can actually handle some
nonlinear constraints, as people noticed that some techniques are actually
more general than just for linear constraints, e.g., interior points methods
can also solve second-order cone problems. However, you will notice serious
performance downgrades as these non-linearity is much more difficult to
handle. If your constraints and objectives get too complex, they may also no
longer be a viable option. Luckily, there currently is a lot of movement in
this area and you can expect that the big solvers (like Gurobi, COPT, Xpress,
etc.) will get better and better in handling these problems. If you have
smaller optimization problems of (nearly) any kind, you may want to look into:
- [SciPy](https://docs.scipy.org/doc/scipy/reference/optimize.html): SciPy is
a Python library that offers a wide range of optimization algorithms. Do not
expect it to get anywhere near the performance of a specialized solver, but
it gives you a bunch of different options to solve a multitude of problems.
- **Modeling Languages:** Modeling languages provide a high-level, user-friendly
interface for formulating optimization problems, focusing on the challenges of
developing and maintaining models that accurately reflect real-world
scenarios. These languages are solver-agnostic, allowing easy switching
between different solvers - such as from the free SCIP solver to the
commercial Gurobi - without modifying the underlying model. They also
facilitate the use of diverse techniques, like transitioning between
constraint programming and mixed integer programming. However, the trade-off
is a potential loss of control and performance for the sake of generality and
simplicity. Some of the most popular modeling languages include:
- [MiniZinc](https://www.minizinc.org/): Very well-documented and free
modelling language that seems to have a high reputation especially in the
academic community. The
[amazing course on constraint programming by Pierre Flener](https://user.it.uu.se/~pierref/courses/COCP/slides/)
also uses MiniZinc. It supports many backends and there are the
[MiniZinc Challenges](https://www.minizinc.org/challenge/), where CP-SAT won
quite a lot of medals.
- [AMPL](https://ampl.com/): AMPL is possibly the most popular modelling
language. It has free and commercial solvers. There is not only extensive
documentation, but even a book on how to use it.
- [GAMS](https://www.gams.com/): This is a commercial system which supports
many solvers and also has gotten a Python-interface. I actually know the
guys from GAMS as they have a location in Braunschweig. They have a lot of
experience in optimization, but I have never used their software myself.
- [pyomo](http://www.pyomo.org/): Pyomo is a Python library that allows you to
model your optimization problem in Python and then let it solve by different
solvers. It is not as high-level as AMPL or GAMS, but it is free and open
source. It is also very flexible and allows you to use Python to model your
problem, which is a huge advantage if you are already familiar with Python.
It actually has support for CP-SAT and could be an option if you just want
to have a quick solution.
- [OR-Tools' MathOpt](https://developers.google.com/optimization/math_opt): A
very new competitor and sibling of CP-SAT. It only supports a few solvers,
but may be still interesting.
- **Specialized Algorithms:** For many optimization problems, there are
specialized algorithms that can be much more efficient than general-purpose
solvers. Examples are:
- [Concorde](http://www.math.uwaterloo.ca/tsp/concorde.html): Concorde is a
solver for the Traveling Salesman Problem that despite its age is still
blazingly fast for many instances.
- [OR-Tools' Routing Solver](https://developers.google.com/optimization/routing):
OR-Tools also comes with a dedicated solver for routing problems.
- [OR-Tools' Network Flows](https://developers.google.com/optimization/flow):
OR-Tools also comes with a dedicated solver for network flow problems.
- ...
- **Approximation Algorithms:** For many difficult optimization problems, you
can find scientific papers that describe approximation algorithms for them.
These algorithms come with some guarantees of not being too far off from the
optimal solution. Some are even proven to achieve the best possible
guarantees. However, you should not directly try to implement such a paper
even if it perfectly fits your problem. There are some approximation
algorithms that are actually practical, but many are not. The guarantees are
usually focussed on artificial worst-case scenarios, and even if the
algorithms can be implemented, they may be beaten by simple heuristics.
Approximation algorithms and their analysis can be quite useful for
understanding the structure of your problem, but their direct practical use is
limited.
- **Meta-Heuristics:** Instead of using a generic solver like CP-SAT, you can
also try to build a custom algorithm for your problem based on some
meta-heuristic pattern, like simulated annealing, genetic algorithms, or tabu
search. Meta-heuristics require some coding, but once you know the pattern,
they are quite straightforward to implement. While there are some libraries to
generalize parts of the algorithms, you could also just write the whole
algorithm yourself. This gives the advantage of truly understanding what is
going on in the algorithm, but you miss a lot of advanced techniques contained
in solvers like CP-SAT. For many optimization problems, you will have
difficulties competing against techniques utilizing advanced solvers in terms
of solution quality. If you just want a quick solution, meta-heuristics can be
a good start.
As evident, there exists a diverse array of tools and techniques for solving
optimization problems. CP-SAT stands out as a versatile approach, particularly
well-suited for combinatorial optimization challenges. If you frequently
encounter these types of problems, becoming proficient with CP-SAT is highly
recommended. Its effectiveness across a broad spectrum of scenarios - excelling
in many - is remarkable for a tool that is both free and open-source.
---
# Part 2: Advanced Topics
## Coding Patterns for Optimization Problems
In this chapter, we will explore various coding patterns that help you structure
your implementations for optimization problems using CP-SAT. These patterns
become especially useful when working on complex problems that need to be solved
continuously and potentially under changing requirements. While we specifically
focus on CP-SAT's Python API, many patterns can be adapted to other solvers and
languages.
In many cases, specifying the model and solving it is sufficient without the
need for careful structuring. However, there are situations where your models
are complex and require frequent iteration, either for performance reasons or
due to changing requirements. In such cases, it is crucial to have a good
structure in place to ensure that you can easily modify and extend your code
without breaking it, as well as to facilitate testing and comprehension. Imagine
you have a complex model and need to adapt a constraint due to new requirements.
If your code is not modular and your test suite is only able to test the entire
model, this small change will force you to rewrite all your tests. After a few
iterations, you might end up skipping the tests altogether, which is a dangerous
path to follow.
Another common issue in complex optimization models is the risk of forgetting to
add some trivial constraints to interlink auxiliary variables, which can render
parts of the model dysfunctional. If the dysfunctional part concerns
feasibility, you might still notice it if you have separately checked the
feasibility of the solution. However, if it involves the objective, such as
penalizing certain combinations, you may not easily notice that your solution is
suboptimal, as the penalties are not applied. Furthermore, implementing complex
constraints can be challenging, and a modular structure allows you to test these
constraints separately to ensure they work as intended. Test-driven development
(TDD) is an effective approach for implementing complex constraints quickly and
reliably.
The field of optimization is highly heterogeneous, and the percentage of
optimizers with a professional software engineering background seems
surprisingly low. Much of the optimization work is done by mathematicians,
physicists, and engineers who have deep expertise in their fields but limited
experience in software engineering. They are usually highly skilled and can
create excellent models, but their code is often not very maintainable and does
not follow software engineering best practices. Many problems are similar enough
that minimal explanation or structure is deemed sufficient—much like creating
plots by copying, pasting, and adjusting a familiar template. While this
approach may not be very readable, it is familiar enough for most people in the
field to understand. Additionally, it is typical for mathematicians to first
document the model and then implement it. From a software engineering
perspective, this workflow resembles the waterfall model, which lacks agility.
There appears to be a lack of literature on agile software development in
optimization, which this chapter seeks to address by presenting some patterns I
have found useful in my work. I asked a few senior colleagues in the field, and
unfortunately, they could not provide any useful resources either or did not
even see the need for such resources. For many use cases, the simple approach is
indeed sufficient. However, I have found that these patterns make my agile,
test-driven workflow much easier, faster, and more enjoyable. Note that this
chapter is largely based on my personal experience due to the limited
availability of references. I would be happy to hear about your experiences and
the patterns you have found useful in your work.
In the following sections, we will start with the basic function-based pattern
and then introduce further concepts and patterns that I have found valuable. We
will work on simple examples where the benefits of these patterns may not be
immediately apparent, but I hope you will see their potential in more complex
problems. The alternative would have been to provide complex examples, which
might have distracted from the patterns themselves.
> [!TIP]
>
> The following patterns focus on details specific to computational
> optimization. However, many optimization engineers come from mathematics or
> physics backgrounds and may not have professional Python or software
> engineering experience. If you are among them, I recommend familiarizing
> yourself in especially with
> [basic data structures and their _comprehensions_](https://docs.python.org/3/tutorial/datastructures.html)
> and elegant loops using
> [itertools](https://docs.python.org/3/library/itertools.html). These tools
> allow you to express your mathematical ideas in Python more elegantly in
> general, and they are especially useful for optimization problems.
>
> Additionally, there are excellent tools to automatically format, check, and
> improve your code, such as [ruff](https://docs.astral.sh/ruff/tutorial/).
> Regularly running `ruff check --fix` and `ruff format` can enhance your code
> quality with minimal effort. Optimally, you will integrate it via a
> [pre-commit hook](https://pre-commit.com/).
>
> For getting started with implementing optimization models in general, I highly
> recommend the blog post
> [The Art Of Not Making It An Art](https://www.gurobi.com/resources/optimization-modeling-the-art-of-not-making-it-an-art/).
> It excellently summarizes the fundamental principles of successfully managing
> an optimization project, independent of the concrete language or solver.
### Simple Function
For straightforward optimization problems, encapsulating the model creation and
solving within a single function is a practical approach. This method is best
suited for simpler cases due to its straightforward nature but lacks flexibility
for more complex scenarios. Parameters such as the time limit and optimality
tolerance can be customized via keyword arguments with default values.
The following Python function demonstrates solving a simple knapsack problem
using CP-SAT. To recap, in the knapsack problem, we select items - each with a
specific weight and value - to maximize total value without exceeding a
predefined weight limit. Given its simplicity, involving only one constraint,
the knapsack problem serves as an ideal model for introductory examples.
```python
from ortools.sat.python import cp_model
from typing import List
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
status = solver.solve(model)
# Extract solution
return (
# Return indices of selected items
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
```
You can also add some more flexibility by allowing any solver parameters to be
passed to the solver.
```python
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*,
time_limit: int = 900,
opt_tol: float = 0.01,
**kwargs,
) -> List[int]:
# initialize the model
model = cp_model.CpModel()
# ...
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
for key, value in kwargs.items():
setattr(solver.parameters, key, value)
# ...
```
Add some unit tests in some separate file (e.g., `test_knapsack.py`) to ensure
that the model works as expected.
> [!TIP]
>
> Write the tests before you write the code. This approach is known as
> test-driven development (TDD) and can help you to structure your code better
> and to ensure that your code works as expected. It also helps you to think
> about the API of your function before you start implementing it.
```python
# Make sure you have a proper project structure and can import your function
from myknapsacksolver import solve_knapsack
def test_knapsack_empty():
# Always good to have a test for the trivial case. The more trivial the
# case, the more likely it is that you forget it.
assert solve_knapsack([], [], 0) == []
def test_knapsack_nothing_fits():
# If nothing fits, we should get an empty solution
assert solve_knapsack([10, 20, 30], [1, 2, 3], 5) == []
def test_knapsack_one_item():
# If only one item fits, we should get this item
assert solve_knapsack([10, 20, 30], [1, 2, 3], 10) == [0]
def test_knapsack_all_items():
# If all items fit, we should get all items
assert solve_knapsack([10, 20, 30], [1, 2, 3], 100) == [0, 1, 2]
```
Using pytest, you can run all tests in the project with `pytest .`. Check
[Real Python](https://realpython.com/pytest-python-testing/) for a good tutorial
on pytest.
### Logging the Model Building
When working with larger optimization problems, logging the model-building
process can be essential to find and fix issues. Often, the problem lies not
within the solver but in the model building itself.
In the following example, we add some basic logging to the solver function to
give us some insights into the model-building process. This logging can be
easily activated or deactivated by the logging framework, allowing us to use it
not only during development but also in production, where you usually deactivate
a lot of logging to save resources.
If you do not know about the logging framework of Python, this is an excellent
moment to learn about it. I consider it an essential skill for production code
and this and similar frameworks are used for most production code in any
language. The official Python documentation contains a
[good tutorial](https://docs.python.org/3/howto/logging.html). There are people
that prefer other logging frameworks, but it comes with Python and is good
enough for most use cases, definitely better than using the badly configurable
`print` statement.
```python
import logging
from ortools.sat.python import cp_model
from typing import List
# Configure the logging framework if it is not already configured.
# We are setting it to debug level, as we are still developing the code.
logging.basicConfig(format="%(asctime)s - %(message)s", level=logging.DEBUG)
_logger = logging.getLogger(__name__) # get a logger for the current module
def solve_knapsack(
weights: List[int],
values: List[int],
capacity: int,
*, # Make the following arguments keyword-only
time_limit: int = 900,
opt_tol: float = 0.01,
) -> List[int]:
_logger.debug("Building the knapsack model")
# initialize the model
model = cp_model.CpModel()
n = len(weights) # Number of items
_logger.debug("Number of items: %d", n)
if n > 0:
if _logger.isEnabledFor(logging.DEBUG):
# Only calculate min, mean, and max if we actually log it
_logger.debug(
"Min/Mean/Max weight: %d/%.2f/%d",
min(weights),
sum(weights) / n,
max(weights),
)
_logger.debug(
"Min/Mean/Max value: %d/%.2f/%d", min(values), sum(values) / n, max(values)
)
# Decision variables for items
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
# Capacity constraint
model.add(sum(weights[i] * x[i] for i in range(n)) <= capacity)
# Objective function to maximize value
model.maximize(sum(values[i] * x[i] for i in range(n)))
# Log the model
_logger.debug("Model created with %d items", n)
# Solve the model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit # Solver time limit
solver.parameters.relative_gap_limit = opt_tol # Solver optimality tolerance
_logger.debug(
"Starting the solution process with time limit %d seconds", time_limit
)
status = solver.solve(model)
# Extract solution
selected_items = (
[i for i in range(n) if solver.value(x[i])]
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]
else []
)
_logger.debug("Selected items: %s", selected_items)
return selected_items
```
We will not use logging in the following examples to save space, but you should
consider adding it to your code.
> [!TIP]
>
> A great hack you can do with the logging framework is that you can easily hook
> into your code and do analysis beyond the simple logging. You can simply write
> a handler that, e.g., waits for the tag `"Selected items: %s"` and then can
> directly access the selected items, as the actual object is passed to the
> handler (and not just the string). This can be very useful to gather
> statistics or to visualize the search process, without having to change the
> (production) code.
### Custom Data Classes for Instances, Configurations, and Solutions
Incorporating serializable data classes based on strict schema to manage
instances, configurations, and solutions significantly enhances code readability
and maintainability. These classes also facilitate documentation, testing, and
ensure data consistency across larger projects where data exchange among
different components is necessary.
One popular library for this purpose is
[Pydantic](https://docs.pydantic.dev/latest/). It is easy to use and provides
substantial functionality out of the box. The following code introduces data
classes for the instance, configuration, and solution of the knapsack problem.
While Python's duck typing is great for rapidly developing internal data flow,
it can be problematic for interfaces. Users will often misuse the interface in
unexpected ways, and you will be blamed for it. Pydantic helps mitigate these
issues by providing a clear interface and validating input data. Additionally,
you can create an API for your code effortlessly using FastAPI, which is built
on top of Pydantic.
```python
# pip install pydantic
from pydantic import (
BaseModel,
PositiveInt,
NonNegativeFloat,
PositiveFloat,
Field,
model_validator,
)
class KnapsackInstance(BaseModel):
# Defines the knapsack instance to be solved.
weights: list[PositiveInt] = Field(..., description="The weight of each item.")
values: list[PositiveInt] = Field(..., description="The value of each item.")
capacity: PositiveInt = Field(..., description="The capacity of the knapsack.")
@model_validator(mode="after")
def check_lengths(cls, v):
if len(v.weights) != len(v.values):
raise ValueError("Mismatch in number of weights and values.")
return v
class KnapsackSolverConfig(BaseModel):
# Defines the configuration for the knapsack solver.
time_limit: PositiveFloat = Field(
default=900.0, description="Time limit in seconds."
)
opt_tol: NonNegativeFloat = Field(
default=0.01, description="Optimality tolerance (1% gap allowed)."
)
log_search_progress: bool = Field(
default=False, description="Whether to log the search progress."
)
class KnapsackSolution(BaseModel):
# Defines the solution of the knapsack problem.
selected_items: list[int] = Field(..., description="Indices of selected items.")
objective: float = Field(..., description="Objective value of the solution.")
upper_bound: float = Field(
..., description="Upper bound of the solution, i.e., a proven limit on how good a solution could be."
)
```
> [!WARNING]
>
> Your data schema should be fully prepared for the optimization process,
> requiring no further preprocessing. Data preparation and optimization are both
> complex tasks, and combining them can significantly increase complexity,
> making your code difficult to maintain. Ideally, your optimization code should
> simply iterate over the data and add the corresponding constraints and
> objectives to the model.
The original code needs to be adapted to use these data classes.
```python
from ortools.sat.python import cp_model
def solve_knapsack(
instance: KnapsackInstance, config: KnapsackSolverConfig
) -> KnapsackSolution:
model = cp_model.CpModel()
n = len(instance.weights)
x = [model.new_bool_var(f"x_{i}") for i in range(n)]
model.add(sum(instance.weights[i] * x[i] for i in range(n)) <= instance.capacity)
model.maximize(sum(instance.values[i] * x[i] for i in range(n)))
solver = cp_model.CpSolver()
# Set solver parameters from the configuration
solver.parameters.max_time_in_seconds = config.time_limit
solver.parameters.relative_gap_limit = config.opt_tol
solver.parameters.log_search_progress = config.log_search_progress
# Solve the model and return the solution
status = solver.solve(model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[i for i in range(n) if solver.value(x[i])],
objective=solver.objective_value,
upper_bound=solver.best_objective_bound,
)
return KnapsackSolution(selected_items=[], objective=0, upper_bound=0)
```
You can use the serialization and deserialization capabilities of Pydantic to
quickly generate test cases based on real data. While you cannot be certain that
your code is correct with such tests, they will at least notify you if the logic
changes unexpectedly. If you refactor your code, you will immediately see if its
behavior changes accidentally.
```python
from datetime import datetime
from hashlib import md5
from pathlib import Path
def add_test_case(instance: KnapsackInstance, config: KnapsackSolverConfig):
"""
Quickly generate a test case based on the instance and configuration.
"""
test_folder = Path(__file__).parent / "test_data"
unique_id = (
datetime.now().strftime("%Y-%m-%d-%H-%M-%S")
+ "_"
+ md5(
(instance.model_dump_json() + config.model_dump_json()).encode()
).hexdigest()
)
subfolder = test_folder / "knapsack" / unique_id
subfolder.mkdir(parents=True, exist_ok=True)
with open(subfolder / "instance.json", "w") as f:
f.write(instance.model_dump_json())
with open(subfolder / "config.json", "w") as f:
f.write(config.model_dump_json())
solution = solve_knapsack(instance, config)
with open(subfolder / "solution.json", "w") as f:
f.write(solution.model_dump_json())
def test_saved_test_cases():
test_folder = Path(__file__).parent / "test_data"
for subfolder in test_folder.glob("knapsack/*"):
with open(subfolder / "instance.json") as f:
instance = KnapsackInstance.model_validate_json(f.read())
with open(subfolder / "config.json") as f:
config = KnapsackSolverConfig.model_validate_json(f.read())
with open(subfolder / "solution.json") as f:
solution = KnapsackSolution.model_validate_json(f.read())
new_solution = solve_knapsack(instance, config)
assert (
new_solution.objective <= solution.upper_bound
), "New solution is better than the previous upper bound: One has to be wrong."
assert (
solution.objective <= new_solution.upper_bound
), "Old solution is better than the new upper bound: One has to be wrong."
# Do not test for the selected items, as the solver might return a different solution of the same quality
```
You can now easily generate test cases and validate them with the following
code. Ideally, you should use real instances for this, potentially by
automatically saving 1% of the instances used in production.
```python
# Define a knapsack instance
instance = KnapsackInstance(
weights=[23, 31, 29, 44, 53, 38, 63, 85, 89, 82],
values=[92, 57, 49, 68, 60, 43, 67, 84, 87, 72],
capacity=165,
)
# Define a solver configuration
config = KnapsackSolverConfig(
time_limit=10.0, opt_tol=0.01, log_search_progress=False
)
# Solve the knapsack problem
solution = solve_knapsack(instance, config)
# Add the test case to the test data folder
add_test_case(instance, config)
```
You can also maintain backward compatibility easily by adding default values to
any new fields you add to the data classes.
> [!TIP] One challenge I often face is designing data classes to be as generic
> as possible so that they can be used with multiple solvers and remain
> compatible throughout various stages of the optimization process. For
> instance, a graph might be represented as an edge list, an adjacency matrix,
> or an adjacency list, each with its own pros and cons, complicating the
> decision of which format is optimal for all stages. However, converting
> between different data class formats is typically straightforward, often
> requiring only a few lines of code and having a negligible impact compared to
> the optimization process itself. Therefore, I recommend focusing on
> functionality with your current solver without overcomplicating this aspect.
> There is little harm in having to call a few conversion functions because you
> created separate specialized data classes.
### Solver Class
In many real-world optimization scenarios, problems may require iterative
refinement of the model and solution. For instance, new constraints might only
become apparent after presenting an initial solution to a user or another
algorithm (like a physics simulation, which is to complex to optimize directly
on). In such cases, flexibility is crucial, making it beneficial to encapsulate
both the model and the solver within a single class. This setup facilitates the
dynamic addition of constraints and subsequent re-solving without needing to
rebuild the entire model, potentially even utilizing warm-starting techniques to
improve performance.
We introduce the `KnapsackSolver` class, which encapsulates the entire setup and
solving process of the knapsack problem. We also use the opportunity to directly
split the model-building into smaller methods, which can be useful for more
complex models.
```python
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(
sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
)
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
"""
Prohibit the combination of two items in the solution.
This can be useful if, after presenting the solution to the user, they decide that these two items should not be packed together. After calling this method, you can simply call `solve` again to get a new solution obeying this constraint.
"""
self.model.add(self.x[item_a] + self.x[item_b] <= 1)
```
At first glance, this may look like a cumbersome interface, as we first have to
create a solver object for a specific instance and then call the `solve` method.
However, this structure accommodates many use cases, and I use variations of it
for most of my projects. Additionally, I sometimes add a simple function that
wraps the solver class to make it easier to use for simple cases.
```python
instance = KnapsackInstance(weights=[1, 2, 3], values=[4, 5, 6], capacity=3)
config = KnapsackSolverConfig(time_limit=10, opt_tol=0.01, log_search_progress=True)
solver = KnapsackSolver(instance, config)
solution = solver.solve()
print(solution)
# Check the solution in a more realistic simulation.
# Assume that the simulation now notices that for some more complex reason,
# we could not express in the optimization model, the first two items should
# not be packed together. We can now prohibit this combination and solve again.
solver.prohibit_combination(0, 1)
# Solve the problem again with the new constraint, but this time
# only allow 5 seconds for the solver.
solution = solver.solve(time_limit=5)
print(solution)
```
Although reusing the solver class primarily spares us from rebuilding the model,
each call to `solve` still initiates a new search from scratch. However,
iteratively refining the model within the same solver instance is more intuitive
to code than treating each iteration as an entirely new problem. Moreover, as we
will demonstrate next, this pattern allows us to improve performance by
leveraging features like warm-starting — offering advantages over stateless
optimization functions.
### Improving Performance with Warm-Starts
As the solver class retains a state and can remember the previous iterations, we
can easily add optimizations that would be cumbersome to implement in a
stateless function. One such optimization is warm-starting, where the solver
uses the previous solution as a starting point or "hint" for the next iteration.
This technique can significantly speed up the solving process, as the solver can
often use the previous solution as a good starting point for repair, even if the
previous solution becomes infeasible due to a newly added constraint. This will
of course only have an advantage if the added constraint does not change the
problem fundamentally but only requires a part of the solution to be changed.
Because repairing an infeasible hint can be computationally expensive, CP-SAT
handles this process carefully. You can instruct CP-SAT to attempt repairing the
hint by setting `solver.parameters.repair_hint = True`. Additionally, you can
adjust the limit on how much effort CP-SAT should spend repairing the hint using
`solver.parameters.hint_conflict_limit`. For example, setting
`solver.parameters.hint_conflict_limit = 10` controls how many conflicts CP-SAT
will resolve before giving up.
Here is an example of how to implement this in code:
```python
class KnapsackSolver:
# ...
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
# Tell CP-SAT to repair the hint if it is infeasible
self.solver.parameters.repair_hint = True
self.solver.parameters.hint_conflict_limit = 20
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
# There is a solution, set it as a hint for the next solve
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
# ...
```
To further improve this approach, you could add a heuristic to repair the hint.
A feasible hint is much more valuable than one that needs significant repair.
For instance, if the hint is infeasible due to a prohibited combination of
items, you could simply drop the least valuable item to make the hint valid.
> [!WARNING]
>
> A common mistake when trying to improve the performance of iterative
> optimization is adding the previous bound as a constraint. Although this
> approach might let CP-SAT resume directly from the previous bound, it often
> limits CP-SAT's ability to find better solutions. This happens because it adds
> a strong constraint unrelated to the problem's feasibility, which can
> interfere with various internal algorithms (such as reducing the effectiveness
> of linear relaxation).
>
> If bounds significantly affect performance, consider using a callback to check
> if the current objective is sufficiently close to the previous bound and stop
> the search if it is. This approach avoids interfering with CP-SAT's
> optimization capabilities, though callbacks do introduce some overhead.
>
> As an exercise to understand why reusing bounds is challenging, try
> implementing a branch-and-bound algorithm for a simple problem like the
> Knapsack Problem - it is a relatively straightforward way to gain insight.
### Exchangeable Objective / Multi-Objective Optimization
In real-world scenarios, objectives are often not clearly defined. Typically,
there are multiple objectives with different priorities, making it challenging
to combine them. Consider the Knapsack problem, representing a logistics issue
where we aim to transport the maximum value of goods in a single trip. Given the
values and weights of the goods, our primary objective is to maximize the packed
goods' value. However, after computing and presenting the solution, we might be
asked to find an alternative solution that does not fill the truck as much, even
if it means accepting up to a 5% decrease in value.
| [](https://xkcd.com/388/) |
| :----------------------------------------------------------------------------------------------------------------------------------------------------: |
| Which fruit is the best one? Many problems are multi-objective and there is no clear single objective. By [xkcd](https://xkcd.com/388/) (CC BY-NC 2.5) |
To handle this, we can optimize in two phases. First, we maximize the value
under the weight constraint. Next, we add a constraint that the value must be at
least 95% of the initial solution's value and change the objective to minimize
the weight. This iterative process can continue through multiple phases,
exploring the Pareto front of the two objectives. More complex problems can be
tackled using similar approaches.
A challenge with this method is avoiding the creation of multiple models and
restarting from scratch in each phase. Since we have a solution close to the new
one and changing the objective does not influence feasibility, it is an
excellent opportunity to use the current solution as a hint for the next solve.
The following code demonstrates how to extend a solver class to support
exchangeable objectives. It includes fixing the current objective value to
prevent degeneration and using the current solution as a hint.
We created a member `_objective` to store the current objective function and
added methods to set the objective to maximize value or minimize weight. We also
introduced methods to set the solution as a hint for the next solve which will
automatically be called if the `solve` found a feasible solution. To not
degenerate on previous objectives, we added a method to fix the current
objective value based on some ratio.
```python
class MultiObjectiveKnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self.n = len(instance.weights)
self.x = [self.model.new_bool_var(f"x_{i}") for i in range(self.n)]
self._objective = 0
self._build_model()
self.solver = cp_model.CpSolver()
def set_maximize_value_objective(self):
"""Set the objective to maximize the value of the packed goods."""
self._objective = sum(
value * x_i for value, x_i in zip(self.instance.values, self.x)
)
self.model.maximize(self._objective)
def set_minimize_weight_objective(self):
"""Set the objective to minimize the weight of the packed goods."""
self._objective = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.minimize(self._objective)
def _set_solution_as_hint(self):
"""Use the current solution as a hint for the next solve."""
for i, v in enumerate(self.model.proto.variables):
v_ = self.model.get_int_var_from_proto_index(i)
assert v.name == v_.name, "Variable names should match"
self.model.add_hint(v_, self.solver.value(v_))
def fix_current_objective(self, ratio: float = 1.0):
"""Fix the current objective value to prevent degeneration."""
if ratio == 1.0:
self.model.add(self._objective == self.solver.objective_value)
elif ratio > 1.0:
self.model.add(self._objective <= ceil(self.solver.objective_value * ratio))
else:
self.model.add(
self._objective >= floor(self.solver.objective_value * ratio)
)
def _add_constraints(self):
"""Add the weight constraint to the model."""
used_weight = sum(
weight * x_i for weight, x_i in zip(self.instance.weights, self.x)
)
self.model.add(used_weight <= self.instance.capacity)
def _build_model(self):
"""Build the initial model with constraints and objective."""
self._add_constraints()
self.set_maximize_value_objective()
def solve(self, time_limit: float | None = None) -> KnapsackSolution:
"""Solve the knapsack problem and return the solution."""
self.solver.parameters.max_time_in_seconds = time_limit if time_limit else self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
self._set_solution_as_hint()
return KnapsackSolution(
selected_items=[
i for i in range(self.n) if self.solver.value(self.x[i])
],
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
```
We can use the `MultiObjectiveKnapsackSolver` class as follows:
```python
config = KnapsackSolverConfig(time_limit=15, opt_tol=0.01, log_search_progress=True)
solver = MultiObjectiveKnapsackSolver(instance, config)
solution_1 = solver.solve()
# maintain at least 95% of the current objective value
solver.fix_current_objective(0.95)
# change the objective to minimize the weight
solver.set_minimize_weight_objective()
solution_2 = solver.solve(time_limit=10)
```
There are more advanced and precise methods for computing the
[Pareto front](https://en.wikipedia.org/wiki/Pareto_front), but
[multi-objective optimization](https://en.wikipedia.org/wiki/Multi-objective_optimization)
is a complex field of research in its own right. If your problem is already
challenging with a single objective, adding more objectives will only increase
the difficulty.
Using the shown approach of lexicographic optimization (with relaxation) or
combining multiple objectives into a single one, for example by adding them with
different weights, is often a reasonable compromise. You could also use
heuristics to explore the solution space around an initial solution obtained
with CP-SAT.
However, multi-objective optimization remains a challenging topic, and even
experts rely on significant trial and error to achieve satisfactory results, as
compromises are often unavoidable.
### Variable Containers
In complex models, variables play a crucial role and can span the entire model.
While managing variables as a list or dictionary may suffice for simple models,
this approach becomes cumbersome and error-prone as the model's complexity
increases. A single mistake in indexing can introduce subtle errors, potentially
leading to incorrect results that are difficult to trace.
As variables form the foundation of the model, refactoring them becomes more
challenging as the model grows. Therefore, it is crucial to establish a robust
management system early on. Encapsulating variables in a dedicated class ensures
that they are always accessed correctly. This approach also allows for the easy
addition of new variables or modifications in their management without altering
the entire model.
Furthermore, incorporating clear query methods helps maintain the readability
and manageability of constraints. Readable constraints, free from complex
variable access patterns, ensure that the constraints accurately reflect the
intended model.
In the following code, we introduce the `_ItemVariables` class to the
`KnapsackSolver`, which acts as a container for the decision variables
associated with the knapsack items. This class not only creates these variables
but also offers several utility methods to interact with them, improving the
clarity and maintainability of the code.
```python
from typing import Generator, Tuple, List
class _ItemSelectionVars:
def __init__(self, instance: KnapsackInstance, model: cp_model.CpModel, var_name: str = "x"):
self.instance = instance
self.x = [model.new_bool_var(f"{var_name}_{i}") for i in range(len(instance.weights))]
def __getitem__(self, i: int) -> cp_model.IntVar:
return self.x[i]
def packs_item(self, i: int) -> cp_model.IntVar:
return self.x[i]
def extract_packed_items(self, solver: cp_model.CpSolver) -> List[int]:
return [i for i, x_i in enumerate(self.x) if solver.value(x_i)]
def used_weight(self) -> cp_model.LinearExprT:
return sum(weight * x_i for weight, x_i in zip(self.instance.weights, self.x))
def packed_value(self) -> cp_model.LinearExprT:
return sum(value * x_i for value, x_i in zip(self.instance.values, self.x))
def iter_items(
self,
weight_lb: float = 0.0,
weight_ub: float = float("inf"),
value_lb: float = 0.0,
value_ub: float = float("inf"),
) -> Generator[Tuple[int, cp_model.IntVar], None, None]:
"""
An example for a more complex query method, which would allow use to
iterate over all items that fulfill certain conditions.
"""
for i, (weight, x_i) in enumerate(zip(self.instance.weights, self.x)):
if (
weight_lb <= weight <= weight_ub
and value_lb <= self.instance.values[i] <= value_ub
):
yield i, x_i
```
This class can be used in the `KnapsackSolver` that handles the higher level
logic, i.e., the high level specification of what the model should do, while
details can be hidden in the container class.
```python
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._build_model()
self.solver = cp_model.CpSolver()
def _add_constraints(self):
self.model.add(self._item_vars.used_weight() <= self.instance.capacity)
def _add_objective(self):
self.model.maximize(self._item_vars.packed_value())
def _build_model(self):
self._add_constraints()
self._add_objective()
def solve(self) -> KnapsackSolution:
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def prohibit_combination(self, item_a: int, item_b: int):
self.model.add_at_most_one(self._item_vars.packs_item(item_a),
self._item_vars.packs_item(item_b))
```
For example,
`self.model.add(self._item_vars.used_weight() <= self.instance.capacity)` now
directly expresses what the constraint does, making the code more readable and
less error-prone. You can actually hide additional optimizations in the
container class, without influencing the higher-level code in the actual solver.
For example, the container class could decide to automatically replace all item
variables that cannot fit into the knapsack due to their weight with a constant.
You can also reuse the variable type, e.g., if you suddenly have two knapsacks
to fill. The following code demonstrates how to quickly extend the solver to
handle two knapsacks, without sacrificing readability or maintainability.
```python
class KnapsackSolver:
def __init__(self, # ...
):
#...
self._knapsack_a = _ItemSelectionVars(instance, self.model, var_name="x1")
self._knapsack_b = _ItemSelectionVars(instance, self.model, var_name="x2")
#...
def _add_constraints(self):
self.model.add(self._knapsack_a.used_weight() <= self.instance.capacity_1)
self.model.add(self._knapsack_b.used_weight() <= self.instance.capacity_2)
self.model.add(self._knapsack_a.used_weight() + self._knapsack_b.used_weight() <= self.instance.capacity_total)
# Add a constraint that items cannot be packed in both knapsacks
for i in range(len(instance.weights)):
self.model.add_at_most_one(self._knapsack_a.packs_item(i), self._knapsack_b.packs_item(i))
def _add_objective(self):
self.model.maximize(self._knapsack_a.packed_value() + self._knapsack_b.packed_value())
```
> [!WARNING]
>
> Do not create such a container class for simple models where the container
> would only wrap a list or a dictionary without adding any additional
> functionality. In such cases, directly using the list or dictionary is
> preferable, as it is more concise and easier to understand. The same is true
> for individual variables that do not need a container at all.
### Lazy Variable Construction
In models with numerous auxiliary variables, often only a subset is actually
used by the constraints. Attempting to create only the variables that are needed
can require complex code to ensure that exactly the right variables are
generated. If the model is extended later, this process becomes even more
complicated, as you may not know upfront which variables will be needed. This is
where lazy variable construction comes into play. By creating variables only
when they are accessed, we ensure that only necessary variables are generated,
reducing memory usage and computational overhead. While this approach might be
more expensive if most variables end up being used anyway, it can save
significant resources when only a small subset is actually needed.
To illustrate this concept, we introduce the `_CombiVariables` class. This class
manages auxiliary variables that indicate when a pair of items is packed
together, allowing us to assign additional bonuses for packing certain items
together. Theoretically, the number of possible item combinations is quadratic
in the number of items, but in practice, only a few may be relevant. By creating
these variables lazily—only when they are accessed—we reduce memory usage and
computational overhead.
```python
class _CombiVariables:
def __init__(
self,
instance: KnapsackInstance,
model: cp_model.CpModel,
item_vars: _ItemSelectionVars,
):
self.instance = instance
self.model = model
self.item_vars = item_vars
self.bonus_vars = {}
def __getitem__(self, item_pair: Tuple[int, int]) -> cp_model.IntVar:
i, j = sorted(item_pair)
if (i, j) not in self.bonus_vars:
var = self.model.NewBoolVar(f"bonus_{i}_{j}")
self.model.add(
self.item_vars.packs_item(i) + self.item_vars.packs_item(j) >= 2 * var
)
self.bonus_vars[(i, j)] = var
return self.bonus_vars[(i, j)]
```
In the `KnapsackSolver`, we can now treat these variables as if they were all
pre-created, without worrying about the underlying optimization. Note that we
have moved the creation of the objective function into the `solve` method, as
adding bonuses for item combinations will modify the objective function. Also,
by encapsulating item variables into a separate class (`_ItemSelectionVars`), we
can easily pass them around and use them in other components.
```python
class KnapsackSolver:
def __init__(self, instance: KnapsackInstance, config: KnapsackSolverConfig):
self.instance = instance
self.config = config
self.model = cp_model.CpModel()
self._item_vars = _ItemSelectionVars(instance, self.model)
self._bonus_vars = _CombiVariables(instance, self.model, self._item_vars)
self._objective_terms = [self._item_vars.packed_value()] # Initial objective terms
self.solver = cp_model.CpSolver()
def solve(self) -> KnapsackSolution:
self.model.maximize(sum(self._objective_terms))
self.solver.parameters.max_time_in_seconds = self.config.time_limit
self.solver.parameters.relative_gap_limit = self.config.opt_tol
self.solver.parameters.log_search_progress = self.config.log_search_progress
status = self.solver.solve(self.model)
if status in [cp_model.OPTIMAL, cp_model.FEASIBLE]:
return KnapsackSolution(
selected_items=self._item_vars.extract_packed_items(self.solver),
objective=self.solver.objective_value,
upper_bound=self.solver.best_objective_bound,
)
return KnapsackSolution(
selected_items=[], objective=0, upper_bound=float("inf")
)
def add_bonus(self, item_a: int, item_b: int, bonus: int):
bonus_var = self._bonus_vars[(item_a, item_b)]
self._objective_terms.append(bonus * bonus_var)
```
> [!TIP]
>
> If we are sure to only call `add_bonus` for a pair of items once, we could
> also save us the trouble of storing the bonus variables and just create and
> add them to the objective function directly in the `add_bonus` method. There
> is no need to store the variable handle if we do not need it later, as CP-SAT
> will take care of the variable's lifecycle.
### Submodels
We can further enhance our modeling approach by encapsulating entire sections of
the model—not just individual variables—into separate submodels. This technique
is particularly useful for complex models where different components are loosely
connected. By partitioning the model into smaller, more manageable submodels, we
improve modularity and maintainability. Submodels communicate with the main
model through shared variables, effectively hiding internal details like
auxiliary variables. If requirements change, we can often reconfigure or replace
specific submodels without affecting the rest of the model. In larger contexts,
it is also common for logic to repeat in different optimization problems of the
system, so building a collection of submodels allows us to quickly assemble new
models using reusable components.
For instance, piecewise linear functions can be modeled as submodels, as
demonstrated with the `PiecewiseLinearConstraint` class in
[piecewise_linear_function.py](https://github.com/d-krupke/cpsat-primer/blob/main/utils/piecewise_functions/piecewise_linear_function.py).
Each submodel handles a piecewise linear function independently, interfacing
with the main model through shared `x` and `y` variables. By encapsulating the
logic for each piecewise function in a dedicated class, we make it reusable and
testable in isolation.
```python
from ortools.sat.python import cp_model
requirements_1 = (3, 5, 2)
requirements_2 = (2, 1, 3)
model = cp_model.CpModel()
buy_1 = model.new_int_var(0, 1_500, "buy_1")
buy_2 = model.new_int_var(0, 1_500, "buy_2")
buy_3 = model.new_int_var(0, 1_500, "buy_3")
produce_1 = model.new_int_var(0, 300, "produce_1")
produce_2 = model.new_int_var(0, 300, "produce_2")
model.add(produce_1 * requirements_1[0] + produce_2 * requirements_2[0] <= buy_1)
model.add(produce_1 * requirements_1[1] + produce_2 * requirements_2[1] <= buy_2)
model.add(produce_1 * requirements_1[2] + produce_2 * requirements_2[2] <= buy_3)
# You can find the PiecewiseLinearFunction and PiecewiseLinearConstraint classes in the utils directory
from piecewise_functions import PiecewiseLinearFunction, PiecewiseLinearConstraint
# Define the functions for the costs
costs_1 = [(0, 0), (1000, 400), (1500, 1300)]
costs_2 = [(0, 0), (300, 300), (700, 500), (1200, 600), (1500, 1100)]
costs_3 = [(0, 0), (200, 400), (500, 700), (1000, 900), (1500, 1500)]
f_costs_1 = PiecewiseLinearFunction(
xs=[x for x, y in costs_1], ys=[y for x, y in costs_1]
)
f_costs_2 = PiecewiseLinearFunction(
xs=[x for x, y in costs_2], ys=[y for x, y in costs_2]
)
f_costs_3 = PiecewiseLinearFunction(
xs=[x for x, y in costs_3], ys=[y for x, y in costs_3]
)
# Define the functions for the gains
gain_1 = [(0, 0), (100, 800), (200, 1600), (300, 2000)]
gain_2 = [(0, 0), (80, 1000), (150, 1300), (200, 1400), (300, 1500)]
f_gain_1 = PiecewiseLinearFunction(
xs=[x for x, y in gain_1], ys=[y for x, y in gain_1]
)
f_gain_2 = PiecewiseLinearFunction(
xs=[x for x, y in gain_2], ys=[y for x, y in gain_2]
)
# Create y >= f(x) constraints for the costs
x_costs_1 = PiecewiseLinearConstraint(model, buy_1, f_costs_1, upper_bound=False)
x_costs_2 = PiecewiseLinearConstraint(model, buy_2, f_costs_2, upper_bound=False)
x_costs_3 = PiecewiseLinearConstraint(model, buy_3, f_costs_3, upper_bound=False)
# Create y <= f(x) constraints for the gains
x_gain_1 = PiecewiseLinearConstraint(model, produce_1, f_gain_1, upper_bound=True)
x_gain_2 = PiecewiseLinearConstraint(model, produce_2, f_gain_2, upper_bound=True)
# Maximize the gains minus the costs
model.maximize(x_gain_1.y + x_gain_2.y - (x_costs_1.y + x_costs_2.y + x_costs_3.y))
```
Testing complex optimization models is often challenging because outputs can be
sensitive to small changes in the model. Even with a good test case, detected
errors may be difficult to trace. By extracting elements into submodels, you can
test these submodels independently, ensuring they work correctly before
integrating them into the main model.
Submodels are usually much simpler than the overall problem, making them easy to
optimize and, thus, fast to test their optimal solution.
```python
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
# Using the submodel
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
model.maximize(c.y)
# Checking its behavior
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL
assert solver.value(c.y) == 10
assert solver.value(x) == 10
```
Alternatively, testing for feasibility or infeasibility can be a good choice,
especially if the submodel does not directly correspond to an optimization
problem on its own.
```python
from ortools.sat.python import cp_model
def test_piecewise_linear_upper_bound_constraint_via_fixation():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values
model.add(x == 10)
model.add(c.y == 10)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.OPTIMAL, "The model should be feasible"
def test_piecewise_linear_upper_bound_constraint_via_fixation_infeasible():
model = cp_model.CpModel()
x = model.new_int_var(0, 20, "x")
f = PiecewiseLinearFunction(xs=[0, 10, 20], ys=[0, 10, 5])
c = PiecewiseLinearConstraint(model, x, f, upper_bound=True)
# Fix the variables to specific values that violate the constraint
model.add(x == 10)
model.add(c.y == 11)
solver = cp_model.CpSolver()
status = solver.solve(model)
assert status == cp_model.INFEASIBLE, "The model should be infeasible"
```
### Embedding CP-SAT in an Application via multiprocessing
If you want to embed CP-SAT in your application for potentially long-running
optimization tasks, you can utilize callbacks to provide users with progress
updates and potentially interrupt the process early. However, one issue is that
the application can only react during the callback. Since the callback is not
always called frequently, this may lead to problematic delays, making it
unsuitable for graphical user interfaces (GUIs) or application programming
interfaces (APIs).
An alternative is to let the solver run in a separate process and communicate
with it using a pipe. This approach allows the solver to be interrupted at any
time, enabling the application to react immediately. Python's multiprocessing
module provides reasonably simple ways to achieve this.
[This example](https://github.com/d-krupke/cpsat-primer/blob/main//examples/embedding_cpsat/)
showcases such an approach. However, for scaling this approach up, you will
actually have to build a task queues where the solver is run by workers. Using
multiprocessing can still be useful for the worker to remain responsive for stop
signals while the solver is running.
|  |
| :----------------------------------------------------------------------------------------------------------------------------------------: |
| _Using multiprocessing, one can build a responsive interface for a solver._ |
[@oulianov](https://github.com/oulianov) deployed it
[here](https://cpsat-embeddings-demo.streamlit.app/) for you to try out in your
browser.
---
# Building an Optimization API (DRAFT)
> [!WARNING]
>
> This chapter is a draft, but feedback is already welcome.
In this chapter, we will create a basic optimization service that performs
computations on a cluster rather than on the client side. This service can be
extended with a straightforward frontend, allowing non-technical users to access
the optimization capabilities. By encapsulating your optimization code within an
easy-to-use API, integration into larger systems becomes more streamlined, and
the separation of algorithm development from deployment is achieved.
While this chapter does not cover every aspect of building a production-ready
API, it will address many important points of it. This foundational knowledge
will enable you to collaborate effectively with your integration experts to
finalize the implementation details, or even do it yourself.
To illustrate these principles, we will develop a simple optimization model for
the Traveling Salesman Problem (TSP). Users will be able to submit an instance
of the TSP, and the API will return a solution. The primary challenge, compared
to many other APIs, is that the TSP is an NP-hard problem, and the CP-SAT solver
may need several minutes to solve even moderately sized instances. Additionally,
we cannot run the solver on the web server; instead, we must distribute the
computation across a cluster. If many requests are received simultaneously, a
request may need to wait before computation can start.
Therefore, this will not be a simple "send request, get response" API. Instead,
we will implement a task queue, returning a task ID that users can use to check
the status of their computation and retrieve the result once it is ready. To
enhance user experience, we will allow users to specify a webhook URL, which we
will call once the computation is complete.
You should be able to easily adapt this API to your own optimization problems,
allowing you to quickly service your optimization algorithms to your colleagues.
## Specifying the Essential Endpoints
Before we start coding, we should specify the endpoints our API will expose, so
we know what we need to implement. This is something you can directly share with
the coworkers who will implement the frontend or other parts of the system, so
they know what to expect and can start working on their parts. It is usually
simple to change the details of the payloads later, but changing the flow of the
API can be much more complex.
The fundamental operations we will support are:
1. **POST /jobs**: This endpoint will accept a JSON payload containing the TSP
instance. The API will create a new task, store the instance, and return a
task ID. The payload will also allow users to specify a webhook URL to call
once the computation is complete.
2. **GET /jobs/{task_id}**: This endpoint will return the status of the task
with the given ID.
3. **GET /jobs/{task_id}/solution**: This endpoint will return the solution of
the task with the given ID, once it is available.
4. **DELETE /jobs/{task_id}**: This endpoint will cancel the task with the given
ID.
5. **GET /jobs**: This endpoint will return a list of all tasks, including their
status and metadata.
By defining these endpoints, we ensure that our API is robust and capable of
handling the core functionalities required for managing and solving TSP
instances. This structure will facilitate user interactions, from submitting
tasks to retrieving solutions and monitoring the status of their requests.
Once we have successfully launched or TSP optimization service, we can
anticipate requests to extend our optimization capabilities to other problems.
Therefore, we should add the prefix `/tsp_solver/v1` to all endpoints to
facilitate future expansions of our API with additional solvers, e.g.,
`knapsack_solver/v1`, or `/tsp_solver/v2_experimental`.
You may ask why we do not just create a new project for each solver and then
just stick them together on a higher level. The reason is that we may want to
share the same infrastructure for all solvers, especially the task queue and the
worker cluster. This can not only be easier to maintain, but also cheaper as
resources can be shared. Therefore, it makes sense to keep them in the same
project. However, it will make sense to separate the actual algorithms from the
API code, and only import the algorithms into our API project. We will not do
this in this chapter, but I personally prefer the algorithms to be as separated
as possible as they are often complex enough on their own.
## Architecture
Having outlined the requirements, we will now consider the architecture of our
system. The system will incorporate the following components:
1. **FastAPI for implementing the endpoints**: FastAPI is a modern,
high-performance web framework for building APIs with Python. We will use
FastAPI to define API endpoints and handle HTTP requests due to its
simplicity, speed, and automatic interactive API documentation.
2. **Redis as a database and communication interface with the workers**: Redis
is an in-memory data structure store that can function as a database, cache,
and message broker. We will utilize Redis for its speed and efficiency in
storing and sharing tasks and solutions, which allows quick access and
automatic expiration of data when it is no longer needed.
3. **Workers managed with RQ (Redis Queue)**: RQ is a simple Python library for
queuing jobs and processing them in the background with workers. This enables
our API to handle tasks asynchronously, offloading computationally expensive
processes to background workers and thereby improving the API's
responsiveness.
To easily manage these components, we will use Docker and Docker Compose to
containerize the API, Redis, and worker instances. This will allow us to quickly
set up and run the service either locally or in a cloud environment.
> [!WARNING]
>
> We will ignore security aspects in this chapter. This service should be only
> for internal use within the own network and not be exposed to the internet. If
> you want to expose it, you should add authentication, rate limiting, and other
> security measures.
### Project Structure
As we only have a single solver in this project, we will neither separate the
solver from the API nor encapsulate the API, but use a simple, flat structure.
You can find the complete project in
[./examples/optimization_api](https://github.com/d-krupke/cpsat-primer/blob/main/examples/optimization_api).
```text
├── app
│ ├── __init__.py
│ ├── config.py
│ ├── db.py
│ ├── main.py
│ ├── models.py
│ ├── solver.py
│ └── tasks.py
├── docker-compose.yml
├── Dockerfile
└── requirements.txt
```
Let us quickly go through the components of the project:
1. **Requirements**: We define the necessary Python packages in a
`requirements.txt` file to ensure that the environment can be easily set up
and replicated. This file includes all dependencies needed for the project.
`requirements.txt` are rather outdated, but they are the simplest way to just
install the dependencies in our container.
2. **Docker Environment**:
- `Dockerfile`: The Dockerfile specifies the Docker image and environment
setup for the API. It ensures that the application runs in a consistent
environment across different machines.
- `docker-compose.yml`: This file configures the services required for the
project, including the API, Redis, and worker instances. Docker Compose
simplifies the process of managing multiple containers, ensuring they are
correctly built and started in the right order. A simple
`docker-compose up -d --build` will get the whole system up and running.
3. **Solver Implementation**:
- `./app/solver.py`: This module contains the implementation of the TSP
solver using CP-SAT. It also specifies the expected input and output data.
4. **Request and Response Models**:
- `./app/models.py`: This module specifies further data models for API
requests and responses.
5. **Database**:
- `./app/db.py`: This module implements a proxy class to interact with Redis,
abstracting database operations for storing and retrieving job requests,
statuses, and solutions.
6. **Config**:
- `./app/config.py`: This module provides configuration functions to set up
the database connection and task queue. By centralizing configuration, we
ensure that other parts of the application do not need to manage connection
details, making the codebase more modular and easier to maintain.
7. **Tasks**:
- `./app/tasks.py`: This module defines the tasks to be outsourced to
workers, which right now only includes the optimization job. Our web server
will only need to get a reference to the task functions in order to queue
them, but not actually run anything of this code. For the workers, this
file will be the entry point.
8. **API**:
- `./app/main.py`: This module implements the FastAPI application with routes
for submitting jobs, checking job statuses, retrieving solutions, and
canceling jobs. This is the entry point for the web server.
### Running the Application
To run the application, we use Docker and Docker Compose to build and run the
containers. This ensures the API and its dependencies are correctly set up. Once
the containers are running, you can interact with the API via HTTP requests.
## Docker Environment
We use Docker to ensure a consistent development and production environment.
Docker allows us to package our application with all its dependencies into a
standardized unit for software development. Docker Compose is used to manage
multi-container applications, defining and running multi-container Docker
applications. As the web server and the workers essentially share the same code,
just with different entry points, we can use the same Docker image for both. The
different entry points will be specified in the `docker-compose.yml`.
### Dockerfile
```dockerfile
# Use an official Python runtime as a parent image
FROM python:3.12-slim
# Set the working directory in the container
WORKDIR /app
# Copy the requirements file into the container at /app
COPY requirements.txt /
# Install any needed packages specified in requirements.txt
RUN pip install --no-cache-dir -r /requirements.txt
# Copy the current directory contents into the container at /app
COPY ./app /app
```
### docker-compose.yml
To get our composition of containers, with the API, Redis, and the workers up
and running, we use the following `docker-compose.yml` file:
```yaml
services:
optimization_api_fastapi: # The web server
build: .
container_name: optimization_api_fastapi
ports: # exposing the API on port 80. Change this if you want to use a different port.
- "80:80"
depends_on: # Ensuring that the web server starts after the database.
- optimization_api_redis
command: python3 -m uvicorn main:app --host 0.0.0.0 --port 80 --reload
optimization_api_redis: # The database. We use the official Redis image.
image: redis:latest
container_name: optimization_api_redis
optimization_api_worker: # The worker
build: .
command: # Running this command will make our container a worker instead of a web server.
rq worker --with-scheduler --url redis://optimization_api_redis:6379/1
depends_on: # Ensuring that the worker starts after the database, as it needs to connect to it.
- optimization_api_redis
deploy:
replicas: 2 # Adding two workers for parallel processing
```
The `docker-compose.yml` file sets up three services:
- `optimization_api_fastapi`: This service builds the FastAPI application,
exposes it on port 80, and ensures it starts after Redis is available.
- `optimization_api_redis`: This service sets up the Redis database from the
official Redis image. We just need to remember the name of the container to
connect to it.
- `optimization_api_worker`: This service builds the worker, which processes
tasks from the queue. We can scale the number of workers by increasing the
number of replicas. Theoretically, these workers could be run on different
machines to scale horizontally.
### Solver
In this section, we will explore the implementation of the optimization
algorithm that we will deploy as an API. Specifically, we will focus on a simple
implementation of the Traveling Salesman Problem (TSP) using the `add_circuit`
constraint from the CP-SAT solver in OR-Tools.
The solver is the core component of our application, responsible for finding the
optimal solution to the TSP instance provided by the user. The algorithm is
implemented directly in the API project for simplicity. However, for more
complex optimization algorithms, it is advisable to separate the algorithm into
a distinct module or project. This separation facilitates isolated testing and
benchmarking of the algorithm and improves the development process, especially
when working in a team where different teams might maintain the API and the
optimization algorithm.
```python
# ./app/solver.py
from typing import Callable
from ortools.sat.python import cp_model
from pydantic import BaseModel, Field
# ---------------------------------------------------------------------
# A precise definition of the input and output data for the TSP solver.
# ---------------------------------------------------------------------
class DirectedEdge(BaseModel):
source: int = Field(..., ge=0, description="The source node of the edge.")
target: int = Field(..., ge=0, description="The target node of the edge.")
cost: int = Field(..., ge=0, description="The cost of traversing the edge.")
class TspInstance(BaseModel):
num_nodes: int = Field(
..., gt=0, description="The number of nodes in the TSP instance."
)
edges: list[DirectedEdge] = Field(
..., description="The directed edges of the TSP instance."
)
class OptimizationParameters(BaseModel):
timeout: int = Field(
default=60,
gt=0,
description="The maximum time in seconds to run the optimization.",
)
class TspSolution(BaseModel):
node_order: list[int] | None = Field(
..., description="The order of the nodes in the solution."
)
cost: float = Field(..., description="The cost of the solution.")
lower_bound: float = Field(..., description="The lower bound of the solution.")
is_infeasible: bool = Field(
default=False, description="Whether the instance is infeasible."
)
# ---------------------------------------------------------------------
# The TSP solver implementation using the CP-SAT solver from OR-Tools.
# ---------------------------------------------------------------------
class TspSolver:
def __init__(
self, tsp_instance: TspInstance, optimization_parameters: OptimizationParameters
):
self.tsp_instance = tsp_instance
self.optimization_parameters = optimization_parameters
self.model = cp_model.CpModel()
self.edge_vars = {
(edge.source, edge.target): self.model.new_bool_var(
f"x_{edge.source}_{edge.target}"
)
for edge in tsp_instance.edges
}
self.model.minimize(
sum(
edge.cost * self.edge_vars[(edge.source, edge.target)]
for edge in tsp_instance.edges
)
)
self.model.add_circuit(
[(source, target, var) for (source, target), var in self.edge_vars.items()]
)
def solve(self, log_callback: Callable[[str], None] | None = None):
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = self.optimization_parameters.timeout
if log_callback:
solver.parameters.log_search_progress = True
solver.log_callback = log_callback
status = solver.Solve(self.model)
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
return TspSolution(
node_order=[
source
for (source, target), var in self.edge_vars.items()
if solver.value(var)
],
cost=solver.objective_value,
lower_bound=solver.best_objective_bound,
)
if status == cp_model.INFEASIBLE:
return TspSolution(
node_order=None,
cost=float("inf"),
lower_bound=float("inf"),
is_infeasible=True,
)
return TspSolution(
node_order=None,
cost=float("inf"),
lower_bound=solver.best_objective_bound,
)
```
> [!TIP]
>
> CP-SAT itself uses Protobuf for its input, output, and configuration. Having
> well-defined data models can help prevent many "garbage in, garbage out"
> issues and ease integration with other systems. It also facilitates testing
> and debugging, as you can simply serialize a specific scenario. For
> configuration, having default values is very helpful, as it allows you to
> extend the configuration without breaking backward compatibility. This can be
> a significant advantage, as you usually do not know all requirements upfront.
> Pydantic performs this job very well and can be used for the web API as well.
> Protobuf, while not Python-specific and therefore more versatile, is more
> complex to use and lacks the same flexibility as Pydantic.
## Request and Response Models
In this section, we will define the request and response models for the API.
These models will facilitate the communication between the client and the server
by ensuring that the data exchanged is structured and validated correctly.
The models are defined in the `models.py` file and include the necessary data
structures for submitting a TSP job request and tracking the status of the job.
```python
# ./app/models.py
"""
This file contains the implementation of additional data models for the optimization API.
"""
from datetime import datetime
from pydantic import BaseModel, HttpUrl, Field
from uuid import UUID, uuid4
from solver import OptimizationParameters, TspInstance
```
The `TspJobRequest` model encapsulates the information required to submit a TSP
job to the API. It includes the TSP instance, optimization parameters, and an
optional webhook URL for notifications upon job completion.
```python
class TspJobRequest(BaseModel):
"""
A request model for a TSP job.
"""
tsp_instance: TspInstance = Field(..., description="The TSP instance to solve.")
optimization_parameters: OptimizationParameters = Field(
default_factory=OptimizationParameters,
description="The optimization parameters.",
)
webhook_url: HttpUrl | None = Field(
default=None, description="The URL to call once the computation is complete."
)
```
An request could look as follows:
```json
{
"tsp_instance": {
"num_nodes": 4,
"edges": [
{"source": 0, "target": 1, "cost": 1},
{"source": 1, "target": 2, "cost": 2},
{"source": 2, "target": 3, "cost": 3},
{"source": 3, "target": 0, "cost": 4},
],
},
"optimization_parameters": {"timeout": 5},
"webhook_url": null,
},
```
The `TspJobStatus` model is used to track the status of a TSP job. It provides
fields to monitor various stages of the job lifecycle, from submission to
completion.
```python
class TspJobStatus(BaseModel):
"""
A response model for the status of a TSP job.
"""
task_id: UUID = Field(default_factory=uuid4, description="The ID of the task.")
status: str = Field(default="Submitted", description="The status of the task.")
submitted_at: datetime = Field(
default_factory=datetime.now, description="The time the task was submitted."
)
started_at: datetime | None = Field(
default=None, description="The time the task was started."
)
completed_at: datetime | None = Field(
default=None, description="The time the task was completed."
)
error: str | None = Field(
default=None, description="The error message if the task failed."
)
```
These models ensure that the data exchanged between the client and the server is
well-defined and validated.
## Database
In this section, we will implement a database proxy to store the tasks and
solutions. For simplicity, we use Redis, which serves as both our database and
task queue. This approach minimizes the need to set up additional databases and
leverages Redis's key-value storage and automatic data expiration features.
The `TspJobDbConnection` class encapsulates the interactions with the Redis
database. It provides methods to register new jobs, update job statuses,
retrieve job requests, statuses, and solutions, list all jobs, and delete jobs.
```python
# ./app/db.py
"""
This file contains a proxy class to interact with the database.
We are using Redis as the database for this example, but the implementation
can be easily adapted to other databases, as the proxy class abstracts the
database operations.
"""
import json
from models import TspJobStatus, TspJobRequest
from solver import TspSolution
from uuid import UUID
import redis
from typing import Optional, List
import logging
```
The class is initialized with a Redis client and an expiration time for the
stored data. The `_get_data` method is a helper that retrieves and parses JSON
data from Redis by key.
```python
class TspJobDbConnection:
def __init__(self, redis_client: redis.Redis, expire_time: int = 24 * 60 * 60):
"""Initialize the Redis connection and expiration time."""
self._redis = redis_client
self._expire_time = expire_time
logging.basicConfig(level=logging.INFO)
def _get_data(self, key: str) -> Optional[dict]:
"""Get data from Redis by key and parse JSON."""
try:
data = self._redis.get(key)
if data is not None:
return json.loads(data)
except redis.RedisError as e:
logging.error(f"Redis error: {e}")
return None
```
The `get_request`, `get_status`, and `get_solution` methods retrieve a TSP job
request, status, and solution, respectively, by their task ID.
```python
def get_request(self, task_id: UUID) -> Optional[TspJobRequest]:
"""Retrieve a TSP job request by task ID."""
data = self._get_data(f"request:{task_id}")
return TspJobRequest(**data) if data else None
def get_status(self, task_id: UUID) -> Optional[TspJobStatus]:
"""Retrieve a TSP job status by task ID."""
data = self._get_data(f"status:{task_id}")
return TspJobStatus(**data) if data else None
def get_solution(self, task_id: UUID) -> Optional[TspSolution]:
"""Retrieve a TSP solution by task ID."""
data = self._get_data(f"solution:{task_id}")
return TspSolution(**data) if data else None
```
The `set_solution` method stores a TSP solution in Redis with an expiration
time. The `register_job` method registers a new TSP job request and status in
Redis.
```python
def set_solution(self, task_id: UUID, solution: TspSolution) -> None:
"""Set a TSP solution in Redis with an expiration time."""
try:
self._redis.set(
f"solution:{task_id}", solution.model_dump_json(), ex=self._expire_time
)
except redis.RedisError as e:
logging.error("Redis error: %s", e)
def register_job(self, request: TspJobRequest) -> TspJobStatus:
"""Register a new TSP job request and status in Redis."""
job_status = TspJobStatus()
try:
pipeline = self._redis.pipeline()
pipeline.set(
f"status:{job_status.task_id}",
job_status.model_dump_json(),
ex=self._expire_time,
)
pipeline.set(
f"request:{job_status.task_id}",
request.model_dump_json(),
ex=self._expire_time,
)
pipeline.execute()
except redis.RedisError as e:
logging.error("Redis error: %s", e)
return job_status
```
The `update_job_status` method updates the status of an existing TSP job. The
`list_jobs` method lists all TSP job statuses.
```python
def update_job_status(self, job_status: TspJobStatus) -> None:
"""Update the status of an existing TSP job."""
try:
self._redis.set(
f"status:{job_status.task_id}",
job_status.model_dump_json(),
ex=self._expire_time,
)
except redis.RedisError as e:
logging.error("Redis error: %s", e)
def list_jobs(self) -> List[TspJobStatus]:
"""List all TSP job statuses."""
try:
status_keys = self._redis.keys("status:*")
data = self._redis.mget(status_keys)
return [TspJobStatus(**json.loads(status)) for status in data if status]
except redis.RedisError as e:
logging.error("Redis error: %s", e)
return []
```
The `delete_job` method deletes a TSP job request, status, and solution from
Redis.
```python
def delete_job(self, task_id: UUID) -> None:
"""Delete a TSP job request, status, and solution from Redis."""
try:
pipeline = self._redis.pipeline()
pipeline.delete(f"status:{task_id}")
pipeline.delete(f"request:{task_id}")
pipeline.delete(f"solution:{task_id}")
pipeline.execute()
except redis.RedisError as e:
logging.error("Redis error: %s", e)
```
## Configuration
The database and task queue require a connection to be established before they
can be used. We provide `get_db_connection` and `get_task_queue` functions in
the `config.py` file for three primary reasons:
- To ensure that the database and task queue are properly set up with the
correct connection details. If we change the Redis host, we only need to
update it in one place.
- To integrate these functions into FastAPI's dependency injection system,
ensuring that the database and task queue are available to the API endpoints
without establishing the connection in each endpoint. This approach also
facilitates testing with a different database.
- To allow both the FastAPI application and the workers to use the same
configuration functions, despite having different entry points.
```python
# ./app/config.py
"""
This file contains the configuration for the optimization API.
For this simple project, it only sets up the database connection and the task queue.
The other parts of the API should not be aware of the specific connection details.
"""
from db import TspJobDbConnection
import redis
from rq import Queue
def get_db_connection() -> TspJobDbConnection:
"""Provides a TspJobDbConnection instance."""
redis_client = redis.Redis(
host="optimization_api_redis", port=6379, decode_responses=True, db=0
)
return TspJobDbConnection(redis_client=redis_client)
def get_task_queue() -> Queue:
"""Provides a Redis Queue instance."""
redis_client = redis.Redis(host="optimization_api_redis", port=6379, db=1)
return Queue(connection=redis_client)
```
## Tasks
With the database in place, we can create the tasks that will run the
optimization. The optimization will run in a separate process and use the
database to communicate with the web server. To keep things simple, we will pass
only the job reference to the task. The task will fetch the necessary data from
the database and update the database with the results. Additionally, by
including an `if __name__ == "__main__":` block, we allow the tasks to be run
via an external task queue as system commands.
The `tasks.py` file contains functions and logic for running the optimization
job in a separate worker process.
```python
# ./app/tasks.py
"""
This file is responsible for running the optimization job in a separate worker.
"""
from config import get_db_connection
from models import TspJobRequest, TspJobStatus
from solver import TspSolver
from datetime import datetime
from uuid import UUID
from db import TspJobDbConnection
import httpx
import logging
```
The `send_webhook` function sends a POST request to the specified webhook URL
with the job status. This allows for asynchronous notifications when the
computation is complete.
```python
def send_webhook(job_request: TspJobRequest, job_status: TspJobStatus) -> None:
if job_request.webhook_url:
try:
# Send a POST request to the webhook URL
response = httpx.post(
url=f"{job_request.webhook_url}", json=job_status.model_dump_json()
)
response.raise_for_status() # Raise an error for bad responses
except httpx.HTTPStatusError as e:
logging.error(
f"HTTP error occurred: {e.response.status_code} - {e.response.text}"
)
except Exception as e:
logging.error(f"An error occurred: {e}")
```
The `run_optimization_job` function fetches the job request from the database,
runs the optimization algorithm, and stores the solution back in the database.
It also updates the job status and sends a webhook notification upon completion.
```python
def run_optimization_job(
job_id: UUID, db_connection: TspJobDbConnection | None = None
) -> None:
"""
Will fetch the job request from the database, run the optimization algorithm,
and store the solution back in the database. Finally, it will send a webhook
to the URL specified in the job. This function may be run on a separate worker,
which is why we do not pass or return data directly, but rather use the database.
"""
if db_connection is None:
db_connection = get_db_connection()
job_status = db_connection.get_status(job_id)
job_request = db_connection.get_request(job_id)
if job_status is None or job_request is None:
return # job got deleted
job_status.status = "Running"
job_status.started_at = datetime.now()
db_connection.update_job_status(job_status)
solver = TspSolver(job_request.tsp_instance, job_request.optimization_parameters)
solution = solver.solve(log_callback=print)
db_connection.set_solution(job_id, solution)
job_status.status = "Completed"
job_status.completed_at = datetime.now()
db_connection.update_job_status(job_status)
send_webhook(job_request, job_status)
```
## API
In this final section, we will build the actual API using FastAPI. This API will
expose endpoints to submit TSP job requests, check job statuses, retrieve
solutions, cancel jobs, and list all jobs. FastAPI provides an efficient and
easy-to-use framework for building web APIs with Python.
The `main.py` file contains the FastAPI application setup and the API routes.
For simplicity, all routes are included in a single file, but in larger
projects, it is advisable to separate them into different modules.
```python
# ./app/main.py
"""
This file contains the main FastAPI application.
For a larger project, we would move the routes to separate files, but for this example, we keep everything in one file.
"""
from uuid import UUID
from fastapi import FastAPI, APIRouter, HTTPException, Depends
from models import TspJobRequest, TspJobStatus
from solver import TspSolution
from config import get_db_connection, get_task_queue
from tasks import run_optimization_job
```
The FastAPI application is initialized with a title and description. An API
router is created to group the routes related to the TSP solver.
```python
app = FastAPI(
title="My Optimization API",
description="This is an example on how to deploy an optimization algorithm based on CP-SAT as an API.",
)
tsp_solver_v1_router = APIRouter(tags=["TSP_solver_v1"])
```
The `post_job` endpoint allows users to submit a new TSP job. The job is
registered in the database, and the optimization task is enqueued in the task
queue for asynchronous processing.
```python
@tsp_solver_v1_router.post("/jobs", response_model=TspJobStatus)
def post_job(
job_request: TspJobRequest,
db_connection=Depends(get_db_connection),
task_queue=Depends(get_task_queue),
):
"""
Submit a new job to solve a TSP instance.
"""
job_status = db_connection.register_job(job_request)
# enqueue the optimization job in the task queue.
# Will return immediately, the job will be run in a separate worker.
task_queue.enqueue(
run_optimization_job,
job_status.task_id,
# adding a 60 second buffer to the job timeout
job_timeout=job_request.optimization_parameters.timeout + 60,
)
return job_status
```
The `get_job` endpoint returns the status of a specific job identified by its
task ID.
```python
@tsp_solver_v1_router.get("/jobs/{task_id}", response_model=TspJobStatus)
def get_job(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Return the status of a job.
"""
status = db_connection.get_status(task_id)
if status is None:
raise HTTPException(status_code=404, detail="Job not found")
return status
```
The `get_solution` endpoint returns the solution of a specific job if it is
available.
```python
@tsp_solver_v1_router.get("/jobs/{task_id}/solution", response_model=TspSolution)
def get_solution(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Return the solution of a job, if available.
"""
solution = db_connection.get_solution(task_id)
if solution is None:
raise HTTPException(status_code=404, detail="Solution not found")
return solution
```
The `cancel_job` endpoint deletes or cancels a job. It does not immediately stop
the job if it is already running.
```python
@tsp_solver_v1_router.delete("/jobs/{task_id}")
def cancel_job(task_id: UUID, db_connection=Depends(get_db_connection)):
"""
Deletes/cancels a job. This will *not* immediately stop the job if it is running.
"""
db_connection.delete_job(task_id)
```
The `list_jobs` endpoint returns a list of all jobs and their statuses.
```python
@tsp_solver_v1_router.get("/jobs", response_model=list[TspJobStatus])
def list_jobs(db_connection=Depends(get_db_connection)):
"""
List all jobs.
"""
return db_connection.list_jobs()
```
Finally, we include the API router in the FastAPI application under the
`/tsp_solver/v1` prefix.
```python
app.include_router(tsp_solver_v1_router, prefix="/tsp_solver/v1")
```
### Running the Application
After you have run `docker-compose up -d --build`, you can access the API at
`http://localhost:80/docs`. This will open the Swagger UI, where you can test
the API. You can submit a job, check the status, and retrieve the solution. You
can also cancel a job or list all jobs.
|  |
| :-------------------------------------------------------------------------------------------------------------: |
| FastAPI comes with a built-in Swagger UI that allows you to interact with the API. |
|  |
| :------------------------------------------------------------------------------------------------------------------------: |
| By clicking on "try it out" you can directly submit a job to the API. |
Here is an instance to try it out: (click to expand)
```json
{
"optimization_parameters": {
"timeout": 5
},
"tsp_instance": {
"num_nodes": 15,
"edges": [
{ "source": 0, "target": 1, "cost": 82 },
{ "source": 1, "target": 0, "cost": 82 },
{ "source": 0, "target": 2, "cost": 35 },
{ "source": 2, "target": 0, "cost": 35 },
{ "source": 0, "target": 3, "cost": 58 },
{ "source": 3, "target": 0, "cost": 58 },
{ "source": 0, "target": 4, "cost": 9 },
{ "source": 4, "target": 0, "cost": 9 },
{ "source": 0, "target": 5, "cost": 13 },
{ "source": 5, "target": 0, "cost": 13 },
{ "source": 0, "target": 6, "cost": 91 },
{ "source": 6, "target": 0, "cost": 91 },
{ "source": 0, "target": 7, "cost": 72 },
{ "source": 7, "target": 0, "cost": 72 },
{ "source": 0, "target": 8, "cost": 16 },
{ "source": 8, "target": 0, "cost": 16 },
{ "source": 0, "target": 9, "cost": 50 },
{ "source": 9, "target": 0, "cost": 50 },
{ "source": 0, "target": 10, "cost": 80 },
{ "source": 10, "target": 0, "cost": 80 },
{ "source": 0, "target": 11, "cost": 92 },
{ "source": 11, "target": 0, "cost": 92 },
{ "source": 0, "target": 12, "cost": 28 },
{ "source": 12, "target": 0, "cost": 28 },
{ "source": 0, "target": 13, "cost": 17 },
{ "source": 13, "target": 0, "cost": 17 },
{ "source": 0, "target": 14, "cost": 97 },
{ "source": 14, "target": 0, "cost": 97 },
{ "source": 1, "target": 2, "cost": 14 },
{ "source": 2, "target": 1, "cost": 14 },
{ "source": 1, "target": 3, "cost": 32 },
{ "source": 3, "target": 1, "cost": 32 },
{ "source": 1, "target": 4, "cost": 41 },
{ "source": 4, "target": 1, "cost": 41 },
{ "source": 1, "target": 5, "cost": 52 },
{ "source": 5, "target": 1, "cost": 52 },
{ "source": 1, "target": 6, "cost": 58 },
{ "source": 6, "target": 1, "cost": 58 },
{ "source": 1, "target": 7, "cost": 20 },
{ "source": 7, "target": 1, "cost": 20 },
{ "source": 1, "target": 8, "cost": 1 },
{ "source": 8, "target": 1, "cost": 1 },
{ "source": 1, "target": 9, "cost": 54 },
{ "source": 9, "target": 1, "cost": 54 },
{ "source": 1, "target": 10, "cost": 75 },
{ "source": 10, "target": 1, "cost": 75 },
{ "source": 1, "target": 11, "cost": 15 },
{ "source": 11, "target": 1, "cost": 15 },
{ "source": 1, "target": 12, "cost": 45 },
{ "source": 12, "target": 1, "cost": 45 },
{ "source": 1, "target": 13, "cost": 94 },
{ "source": 13, "target": 1, "cost": 94 },
{ "source": 1, "target": 14, "cost": 41 },
{ "source": 14, "target": 1, "cost": 41 },
{ "source": 2, "target": 3, "cost": 82 },
{ "source": 3, "target": 2, "cost": 82 },
{ "source": 2, "target": 4, "cost": 44 },
{ "source": 4, "target": 2, "cost": 44 },
{ "source": 2, "target": 5, "cost": 83 },
{ "source": 5, "target": 2, "cost": 83 },
{ "source": 2, "target": 6, "cost": 91 },
{ "source": 6, "target": 2, "cost": 91 },
{ "source": 2, "target": 7, "cost": 78 },
{ "source": 7, "target": 2, "cost": 78 },
{ "source": 2, "target": 8, "cost": 51 },
{ "source": 8, "target": 2, "cost": 51 },
{ "source": 2, "target": 9, "cost": 6 },
{ "source": 9, "target": 2, "cost": 6 },
{ "source": 2, "target": 10, "cost": 81 },
{ "source": 10, "target": 2, "cost": 81 },
{ "source": 2, "target": 11, "cost": 77 },
{ "source": 11, "target": 2, "cost": 77 },
{ "source": 2, "target": 12, "cost": 93 },
{ "source": 12, "target": 2, "cost": 93 },
{ "source": 2, "target": 13, "cost": 97 },
{ "source": 13, "target": 2, "cost": 97 },
{ "source": 2, "target": 14, "cost": 33 },
{ "source": 14, "target": 2, "cost": 33 },
{ "source": 3, "target": 4, "cost": 66 },
{ "source": 4, "target": 3, "cost": 66 },
{ "source": 3, "target": 5, "cost": 47 },
{ "source": 5, "target": 3, "cost": 47 },
{ "source": 3, "target": 6, "cost": 54 },
{ "source": 6, "target": 3, "cost": 54 },
{ "source": 3, "target": 7, "cost": 39 },
{ "source": 7, "target": 3, "cost": 39 },
{ "source": 3, "target": 8, "cost": 98 },
{ "source": 8, "target": 3, "cost": 98 },
{ "source": 3, "target": 9, "cost": 90 },
{ "source": 9, "target": 3, "cost": 90 },
{ "source": 3, "target": 10, "cost": 5 },
{ "source": 10, "target": 3, "cost": 5 },
{ "source": 3, "target": 11, "cost": 27 },
{ "source": 11, "target": 3, "cost": 27 },
{ "source": 3, "target": 12, "cost": 61 },
{ "source": 12, "target": 3, "cost": 61 },
{ "source": 3, "target": 13, "cost": 95 },
{ "source": 13, "target": 3, "cost": 95 },
{ "source": 3, "target": 14, "cost": 19 },
{ "source": 14, "target": 3, "cost": 19 },
{ "source": 4, "target": 5, "cost": 34 },
{ "source": 5, "target": 4, "cost": 34 },
{ "source": 4, "target": 6, "cost": 10 },
{ "source": 6, "target": 4, "cost": 10 },
{ "source": 4, "target": 7, "cost": 20 },
{ "source": 7, "target": 4, "cost": 20 },
{ "source": 4, "target": 8, "cost": 44 },
{ "source": 8, "target": 4, "cost": 44 },
{ "source": 4, "target": 9, "cost": 33 },
{ "source": 9, "target": 4, "cost": 33 },
{ "source": 4, "target": 10, "cost": 29 },
{ "source": 10, "target": 4, "cost": 29 },
{ "source": 4, "target": 11, "cost": 36 },
{ "source": 11, "target": 4, "cost": 36 },
{ "source": 4, "target": 12, "cost": 62 },
{ "source": 12, "target": 4, "cost": 62 },
{ "source": 4, "target": 13, "cost": 77 },
{ "source": 13, "target": 4, "cost": 77 },
{ "source": 4, "target": 14, "cost": 63 },
{ "source": 14, "target": 4, "cost": 63 },
{ "source": 5, "target": 6, "cost": 73 },
{ "source": 6, "target": 5, "cost": 73 },
{ "source": 5, "target": 7, "cost": 6 },
{ "source": 7, "target": 5, "cost": 6 },
{ "source": 5, "target": 8, "cost": 91 },
{ "source": 8, "target": 5, "cost": 91 },
{ "source": 5, "target": 9, "cost": 5 },
{ "source": 9, "target": 5, "cost": 5 },
{ "source": 5, "target": 10, "cost": 61 },
{ "source": 10, "target": 5, "cost": 61 },
{ "source": 5, "target": 11, "cost": 11 },
{ "source": 11, "target": 5, "cost": 11 },
{ "source": 5, "target": 12, "cost": 91 },
{ "source": 12, "target": 5, "cost": 91 },
{ "source": 5, "target": 13, "cost": 7 },
{ "source": 13, "target": 5, "cost": 7 },
{ "source": 5, "target": 14, "cost": 88 },
{ "source": 14, "target": 5, "cost": 88 },
{ "source": 6, "target": 7, "cost": 52 },
{ "source": 7, "target": 6, "cost": 52 },
{ "source": 6, "target": 8, "cost": 86 },
{ "source": 8, "target": 6, "cost": 86 },
{ "source": 6, "target": 9, "cost": 48 },
{ "source": 9, "target": 6, "cost": 48 },
{ "source": 6, "target": 10, "cost": 13 },
{ "source": 10, "target": 6, "cost": 13 },
{ "source": 6, "target": 11, "cost": 31 },
{ "source": 11, "target": 6, "cost": 31 },
{ "source": 6, "target": 12, "cost": 91 },
{ "source": 12, "target": 6, "cost": 91 },
{ "source": 6, "target": 13, "cost": 62 },
{ "source": 13, "target": 6, "cost": 62 },
{ "source": 6, "target": 14, "cost": 30 },
{ "source": 14, "target": 6, "cost": 30 },
{ "source": 7, "target": 8, "cost": 79 },
{ "source": 8, "target": 7, "cost": 79 },
{ "source": 7, "target": 9, "cost": 94 },
{ "source": 9, "target": 7, "cost": 94 },
{ "source": 7, "target": 10, "cost": 58 },
{ "source": 10, "target": 7, "cost": 58 },
{ "source": 7, "target": 11, "cost": 12 },
{ "source": 11, "target": 7, "cost": 12 },
{ "source": 7, "target": 12, "cost": 81 },
{ "source": 12, "target": 7, "cost": 81 },
{ "source": 7, "target": 13, "cost": 2 },
{ "source": 13, "target": 7, "cost": 2 },
{ "source": 7, "target": 14, "cost": 89 },
{ "source": 14, "target": 7, "cost": 89 },
{ "source": 8, "target": 9, "cost": 15 },
{ "source": 9, "target": 8, "cost": 15 },
{ "source": 8, "target": 10, "cost": 94 },
{ "source": 10, "target": 8, "cost": 94 },
{ "source": 8, "target": 11, "cost": 23 },
{ "source": 11, "target": 8, "cost": 23 },
{ "source": 8, "target": 12, "cost": 50 },
{ "source": 12, "target": 8, "cost": 50 },
{ "source": 8, "target": 13, "cost": 79 },
{ "source": 13, "target": 8, "cost": 79 },
{ "source": 8, "target": 14, "cost": 65 },
{ "source": 14, "target": 8, "cost": 65 },
{ "source": 9, "target": 10, "cost": 68 },
{ "source": 10, "target": 9, "cost": 68 },
{ "source": 9, "target": 11, "cost": 81 },
{ "source": 11, "target": 9, "cost": 81 },
{ "source": 9, "target": 12, "cost": 34 },
{ "source": 12, "target": 9, "cost": 34 },
{ "source": 9, "target": 13, "cost": 21 },
{ "source": 13, "target": 9, "cost": 21 },
{ "source": 9, "target": 14, "cost": 16 },
{ "source": 14, "target": 9, "cost": 16 },
{ "source": 10, "target": 11, "cost": 10 },
{ "source": 11, "target": 10, "cost": 10 },
{ "source": 10, "target": 12, "cost": 12 },
{ "source": 12, "target": 10, "cost": 12 },
{ "source": 10, "target": 13, "cost": 60 },
{ "source": 13, "target": 10, "cost": 60 },
{ "source": 10, "target": 14, "cost": 61 },
{ "source": 14, "target": 10, "cost": 61 },
{ "source": 11, "target": 12, "cost": 36 },
{ "source": 12, "target": 11, "cost": 36 },
{ "source": 11, "target": 13, "cost": 78 },
{ "source": 13, "target": 11, "cost": 78 },
{ "source": 11, "target": 14, "cost": 79 },
{ "source": 14, "target": 11, "cost": 79 },
{ "source": 12, "target": 13, "cost": 54 },
{ "source": 13, "target": 12, "cost": 54 },
{ "source": 12, "target": 14, "cost": 33 },
{ "source": 14, "target": 12, "cost": 33 },
{ "source": 13, "target": 14, "cost": 29 },
{ "source": 14, "target": 13, "cost": 29 }
]
}
}
```
## Classical Optimization vs. Machine Learning (and the impact of Quantum Computing)
A prevalent discussion in today's landscape revolves around whether Machine
Learning (ML) or Quantum Computing (QC) could replace classical optimization
methods such as CP-SAT. In this chapter, we will explore the fundamental
differences between Machine Learning and Optimization, demonstrating that these
fields are not interchangeable but rather complementary to each other. By
understanding their distinct strengths and applications, we can better leverage
each approach to solve complex problems effectively.
Following our discussion on these differences, a common question arises: will
Quantum Computing render classical optimization techniques obsolete? To address
this, we will delve into the basic challenges facing Quantum Computing in the
context of Optimization and explain why its impact may be less significant than
often anticipated. This section aims to debunk several myths, some of which are
perpetuated by proponents of Quantum Computing.
Machine Learning excels at **predicting** outcomes based on historical data,
identifying patterns, and making informed guesses, such as estimating the best
solution to an optimization problem based on data patterns. It is adept at
learning and generalizing from data, even if the data is imperfect, provided
there is sufficient quantity. On the other hand, Optimization is powerful for
systematically **searching** for the best solution based on a well-defined
mathematical model, capable of optimizing variables and constraints with
precision, often requiring minimal data. For example, in planning delivery
routes, ML can predict driving times and resource needs based on historical
factors, whereas an optimization solver like CP-SAT is better suited to
determining the most efficient routes by evaluating the interdependencies and
constraints systematically. Both fields enhance decision-making processes when
used together, leveraging ML’s predictive capabilities and Optimization’s
rigorous solution-finding methods.
In the article
[**Four Key Differences Between Mathematical Optimization And Machine Learning**](https://www.forbes.com/councils/forbestechcouncil/2021/06/25/four-key-differences-between-mathematical-optimization-and-machine-learning/),
Edward Rothberg, the CEO of Gurobi, highlights four key differences between
Machine Learning and Optimization:
- **Analytical Focus**: ML is primarily a **predictive** tool that identifies
patterns in historical data to forecast future events, whereas Optimization is
a **prescriptive** tool that uses a digital twin of your environment to
recommend the best possible decisions.
- **Typical Applications**: ML is commonly used for tasks like fraud detection,
speech recognition, and product recommendations—often consumer-facing
applications. Optimization is leveraged for operational decision-making in
areas like production planning, scheduling, and shipment routing.
- **Adaptability**: ML can suffer from "model drift" if the environment changes
significantly, requiring retraining with new data. Optimization models,
however, can be updated more seamlessly to reflect changes in real time but
usually need more upfront effort to build.
- **Maturity**: Both fields have roots tracing back decades, but Optimization
has largely settled into a "plateau of productivity," while ML is currently at
the “peak of inflated expectations” and may face a phase of disillusionment
before stabilizing into broader adoption.
> [!TIP]
>
> You do not have to read this section if you are not interested in my
> arguments. The TL;DR is that neither Machine Learning nor Quantum Computing
> will make CP-SAT (and similar methods) obsolete any time soon, if ever.
> However, Machine Learning is a valuable complement to Optimization.
> [!TIP]
>
> [ML ain't your only hammer: adding mathematical optimisation to the data scientist's toolbox](https://www.youtube.com/watch?v=G0tlyC9Sr3w):
> This 20-minute talk by Dr. Jack Simpson introduces data scientists with a
> machine learning focus to mathematical optimization, highlighting how it
> prescribes optimal decisions under complex constraints and complements ML
> forecasts.
### Using GenAI/LLMs for Optimization
It is indeed possible to ask ChatGPT (or similar large language models) to solve
certain optimization problems, and in simpler cases (like the Knapsack Problem)
it often succeeds by automatically writing Python code that calls an external
solver (e.g., HiGHs). Although this approach may work for small instances, it
generally runs much slower than a dedicated solver and can introduce subtle
errors. In the example below, ChatGPT took around 10 seconds, whereas a
specialized solver would have solved the same instance almost instantly:
|  |  |
| :-----------------------------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------------------------------------: |
| Asking ChatGPT to solve a Knapsack Problem, which it does successfully... | ...but under the hood, it relies on an external solver. |
More advanced versions of ChatGPT (e.g., ChatGPT 4) can tackle somewhat larger
problems but still fall short of solvers like CP-SAT that systematically
evaluate massive search spaces with efficient backtracking and pruning. Large
language models process information sequentially in short "turns", have limited
context windows, and lack specialized heuristics - factors that make them prone
to logical missteps and slower performance as the problem size grows. Repeatedly
generating code or text also creates overhead, and verifying solutions can
require multiple iterations of prompting, further compounding the time cost.
Because of these limitations, LLMs are unlikely to replace robust solvers for
substantial or complex optimization tasks anytime soon. However, current
research on **hybrid AI-OR methods** aims to combine the flexibility of LLMs
(such as quick prototyping and model building) with the powerful search
capabilities of dedicated solvers. As this field evolves, LLMs may increasingly
assist in formulating or refining optimization models while specialized engines
focus on the computationally intensive search. We will revisit these
possibilities in the upcoming section on "Model Building with GenAI/LLMs".
To dig a little deeper into the limitations of LLMs for optimization, consider
the following articles:
- [LLM-ify me - Optimization edition](https://oberdieck.dk/p/llm-in-optimization/):
A blog post exploring the potential of LLMs for optimization.
- [Mind Evolution and the frontier of LLM-based optimization solvers](https://open.substack.com/pub/feasible/p/64-mind-evolution-and-the-frontier?r=49480z&utm_campaign=post&utm_medium=email):
An article from the Feasible newsletter discussing the potential of LLMs for
optimization.
- [Why Solving Multi-agent Path Finding with Large Language Models has not Succeeded Yet](https://arxiv.org/pdf/2401.03630)
- [Look Further Ahead: Testing the Limits of GPT-4 in Path Planning](https://arxiv.org/pdf/2406.12000)
- [Extracting Problem Structure with LLMs for Optimized SAT Local Search](https://arxiv.org/pdf/2501.14630):
This paper demonstrates how an LLM can be used to automatically generate
**start heuristics** from Python code that models a problem as a SAT instance
using the PySAT library. These start heuristics provide the **initial phase**
for a SAT solver, helping it begin the search from a more promising assignment
and enabling it to solve additional instances that would remain unsolved
otherwise.
### Reinforcement Learning
In some cases, an actually viable alternative to optimization solvers like
CP-SAT is Reinforcement Learning. Reinforcement learning can be highly effective
for optimizing very complex problems that are too intricate to model with simple
mathematical formulations. During my dissertation, I applied reinforcement
learning to optimize a multi-agent system where developing a comprehensive
mathematical model was infeasible due to the excessive number of variables and
constraints required to capture the system’s dynamics. Additionally, manually
crafted heuristics proved unable to compete with the performance of a
straightforward reinforcement learning agent, which I implemented with minimal
effort using
[Stable Baselines](https://stable-baselines.readthedocs.io/en/master/). However,
despite reinforcement learning agents being capable of performing many more
iterations to learn about the solution space compared to large language models
(LLMs), they still lack the structured and efficient search capabilities
inherent in classical solvers. Furthermore, designing an appropriate reward
function for reinforcement learning can be challenging and often involves
significant trial and error.
#### Combining Machine Learning and Optimization
Instead of trying to replace optimization solvers like CP-SAT with machine
learning, a more promising approach is to combine the two fields. This can be
achieved in several ways, such as using machine learning to predict parameters
for optimization problems, building optimization proxies, or integrating machine
learning within solvers to guide internal decisions. These methods leverage the
strengths of both fields to enhance decision-making processes and improve
solution quality.
##### Predict-Then-Optimize Variants
Predict-Then-Optimize is a framework that combines machine learning with
optimization. The basic version involves two simple steps: predict and then
optimize. First, a standard ML model (e.g., a regression) is trained to estimate
unknown parameters of the optimization problem, such as costs or demands, using
conventional loss functions like mean squared error. Next, these predicted
parameters are passed to an optimization solver (such as CP-SAT), which produces
a best-possible solution—say, a schedule, route, or resource allocation—based on
the estimated inputs. This approach is effective when the model’s predictive
accuracy is reasonably high, but it can falter if small errors in the
predictions cause large downstream impacts on the decision.
To improve decision quality, more advanced, "decision-focused" variants of
Predict-Then-Optimize incorporate the solver's objective directly into the ML
training process. Rather than merely minimizing standard predictive error, these
methods seek to minimize "regret"—the gap between the cost of the solver's
solution under predicted parameters and the cost of the true optimal solution.
By repeatedly using the solver (or an approximation) during training, they
compute how prediction mistakes translate into suboptimal decisions, and feed
this information back to the ML model's parameters. As a result, the model
learns to predict in a way that preserves or improves the final solution's
quality, even if the raw predictive accuracy on each parameter is not perfectly
precise.
Check out
[this great lecture by Elias Khalil](https://www.youtube.com/watch?v=pZqm-i57gxk)
which was part of a summer school.
> [!TIP]
>
> Uncertainty and unknown parameters frequently arise in optimization problems.
> While the **predict-then-optimize** framework offers a straightforward
> approach, its more advanced variants can help address some of its limitations.
> For even greater robustness, techniques such as **robust optimization**,
> **stochastic programming**, and others provide more effective solutions,
> especially in highly uncertain environments, though they come with increased
> complexity. Numerous research studies explore these and additional methods,
> with the optimal choice depending heavily on the specific application.
##### Optimization Proxies
An optimization proxy is a machine learning model trained to approximate the
input-output behavior of an optimization solver, enabling near-instant decisions
once deployed. Typically, one gathers a large set of problem instances, solves
them offline using a traditional solver to generate "ground truth" solutions,
and then trains an ML model to map inputs (e.g., demands, costs) to outputs (the
solver's decisions). In real-time or large-scale simulation settings—such as
power systems, scheduling, or routing—using the learned proxy bypasses the usual
heavy solve times, providing solutions (or near-solutions) almost instantly.
Because the training data comes directly from the solver, no manual labeling is
required; any number of instances can be generated offline.
However, optimization proxies excel only when repeatedly solving relatively
similar models under stable conditions, and they can struggle when complex
feasibility constraints or drastically changing problem parameters arise. Though
they have found very useful applications in areas like power networks, many
other optimization contexts involve too many shifting variables or intricate
constraints for a simple proxy to handle reliably. Substantial changes to the
problem's structure often require retraining or extensive model adaptation. As a
result, while proxies can be a powerful add-on to speed up certain classes of
problem instances, they are by no means a universal replacement for classical
solvers.
A [short 4min explanation](https://www.youtube.com/watch?v=UAwEZi56cb8) is given
by Pascal Van Hentenryck. And a longer version can be found
[here](https://www.youtube.com/watch?v=NlwxEGtw4QY).
##### Model Building with GenAI/LLMs
An increasingly valuable application of LLMs (or generative AI) in optimization
is assisting with the model building process. Rather than trying to solve an
optimization problem directly, which is often ineffective, these models can help
set up the initial model that a specialized solver will handle. Many
optimization models share similar structures and differ only in certain details,
making LLMs useful for producing core components. Tools like GitHub Co-Pilot can
already generate complex parts of a model, yet they may also introduce subtle
errors that are hard to detect, such as off by one mistakes, inverted
constraints, or swapped indices. It is therefore best to use LLMs as a source of
inspiration and verify their output carefully; otherwise, the time you save
coding might be spent on debugging.
Moreover, your optimization model often represents the backbone of a real world
problem, so it is crucial to understand how it aligns with the underlying
operational or business context. While LLMs can expedite coding, they cannot
replace the human expertise needed to approximate and simplify real world
complexities. If the scenario is critical, you may not want to rely too heavily
on an AI-based approach at this stage. That said, several research projects and
commercial products are already exploring this idea:
1. [A Research Project at Stanford](https://web.stanford.edu/~udell/project-modeling.html)
2. [Gurobi AI Modeling](https://gurobi-ai-modeling.readthedocs.io/en/latest/index.html)
([Quick Overview](https://www.youtube.com/watch?v=8hr_23zdRV4))
3. [Quantagonia](https://www.quantagonia.com/decisionai) provides a solver you
can interact with via chat
4. [Robust and Adaptive Optimization under a Large Language Model Lens](https://arxiv.org/pdf/2501.00568):
A research paper exploring using LLMs for robust optimization.
##### Learning instead of Guessing
Machine learning can also be integrated _inside_ solvers, guiding internal
decisions such as branching strategies, cut selection, or matrix scaling. Rather
than relying on hand-tuned rules alone, the solver gathers data across diverse
problem instances and learns which algorithmic choices best reduce run time or
improve numerical stability. For instance, a model can predict whether "local"
or "global" cutting planes will be more effective on a given instance, or
whether certain scaling methods will avoid ill-conditioned bases. By treating
these decisions as regression tasks - estimating speedup or stability
improvements - machine learning lets the solver adapt and self-tune, ultimately
performing better on a wide spectrum of problems without sacrificing generality.
This
[lecture by Timo Berthold (FICO)](https://www.youtube.com/watch?v=xYKNH3Pqq9A)
gives a good overview of the topic. It has been part of the CO@Work 2024 summer
school, which I actually attended and consider to be absolutely amazing and if
you get the chance to attend, I highly recommend it (as long as you already are
on PhD-level, as it is intense).
A three-hour tutorial by various experts on the topic (including Elias Khalil
and Andrea Lodi), can be found
[here](https://www.youtube.com/watch?v=XVLd7hf6y6M&list=LL&index=20). I highly
recommend watching it, if you are interested in the topic as I had many "aha"
moments during this tutorial.
> [!NOTE]
>
> - [Machine learning augmented branch and bound for mixed integer linear programming](https://link.springer.com/article/10.1007/s10107-024-02130-y):
> This recent paper from 2024 surveys ideas for using machine learning to
> improve branch-and-bound solvers for mixed-integer linear programming.
### Why Quantum Computing Will (Probably) Not Have a Big Impact on Optimization
Before closing this chapter, let us also discuss the impact of Quantum Computing
on Optimization, as this is a question I am frequently asked, usually directly
after having explained why ChatGPT cannot replace CP-SAT.
You often hear claims that quantum computing will revolutionize optimization,
especially regarding the Traveling Salesman Problem (TSP). These claims
frequently state that a new quantum algorithm can solve TSP (a challenging yet
practically important combinatorial optimization problem) for small instance
sizes, while a classical computer would supposedly need billions of years to
handle as few as 20 nodes. (In reality, some published papers still only address
four nodes.) Unfortunately, such claims usually hinge on a theoretical
worst-case runtime of around $O(n^2 2^n)$ for the TSP, which is not
representative of how the problem is handled in practice.
> [!NOTE]
>
> For an accessible and insightful discussion on the myths and exaggerated
> expectations surrounding quantum computing, consult the freely available book
> [_What You Shouldn't Know About Quantum Computers_](https://arxiv.org/abs/2405.15838)
> by Chris Ferrie. This resource offers an excellent opportunity to critically
> examine common misconceptions often perpetuated by science fiction and popular
> science literature.
Although the best-known quantum algorithm runs in $O(1.728^n)$, which is
somewhat better than $O(n^2 2^n)$, it remains exponential and grows very
quickly. Since the TSP is NP-hard, it is unlikely we will ever discover a
(quantum or classical) algorithm whose worst-case runtime does not explode with
instance size. Moreover, real-world or average-case performance can be vastly
different from worst-case performance. In fact, TSP can already be solved
effectively for large instances on classical computers, so many bold claims
about quantum computing's purported advantages in optimization can be misleading
or simply incorrect.
To date, there is no strong evidence suggesting that quantum computing will have
a major impact on optimization. Many experts believe that, at best, quantum
computing might offer only a modest performance advantage in this domain, though
it may have significant implications for cryptology.
> [!TIP]
>
> At a recent consortium meeting, a consultant from a logistics optimization
> firm made a particularly noteworthy remark. According to them, even with the
> advent of a fully functional quantum computer equipped with thousands of
> flawless qubits, its primary utility would lie in marketing. Beyond that, it
> would be little more than "metal trash," offering no tangible value for their
> customers' use cases. This statement prompted humorous objections from quantum
> experts regarding the "metal trash" comment. Nevertheless, the broader
> sentiment that quantum computing is overhyped in the optimization domain was
> widely shared.
To put the Traveling Salesman Problem's difficulty into historical perspective:
In the mid-20th century, the TSP attracted attention through challenges offering
substantial prize money for solving relatively small instances of 33 to 49
cities - already far larger than those currently tackled by many quantum
researchers. As Newsweek reported in **1954**:
> "By an ingenious application of linear programming - a mathematical tool
> recently used to solve production-scheduling problems - it took only a few
> weeks for the California experts to calculate by hand the shortest route to
> cover the 49 cities."
Remarkably, they not only found the shortest route, but also proved it was the
shortest, all by hand in the 1950s. You can read more details in
[this blog post](https://www.math.uwaterloo.ca/tsp/us/history.html). Nowadays,
there is even
[an iPhone app](https://apps.apple.com/us/app/concorde-tsp/id498366515) that can
solve instances of around 1,000 TSP cities to optimality in mere seconds.
[Larger-scale instances](https://www.math.uwaterloo.ca/tsp/optimal/index.html)
(up to 85,900 nodes, solved in 2006) and near-optimal solutions for millions of
cities illustrate how far classical methods have come. In that sense, quantum
computers have a considerable way to go before they can beat even a human with
pen and paper, let alone a classical computer.
Misjudging the difficulty of certain combinatorial problems famously led one
puzzle inventor into unexpected financial trouble. His creation,
[_The Eternity Puzzle_](https://en.wikipedia.org/wiki/Eternity_puzzle), offered
a £1,000,000 prize to anyone who could solve it—a sum that some early estimates
suggested might never be claimed in a human lifespan, given the vast number of
possible configurations. However, instead of brute-forcing every possibility,
two Cambridge mathematicians employed advanced techniques to dramatically narrow
the search space. Similarly, CP-SAT leverages a variety of behind-the-scenes
strategies to tackle complex problems more efficiently than most would
imagine—indeed, many of the methods used to solve The Eternity Puzzle resemble
what CP-SAT does in a more general way.
Thanks to these refined methods, the puzzle was solved in under 18 months - much
sooner than anticipated. Although rumors circulated that the puzzle's inventor,
Christopher Monckton, was forced to sell his mansion to pay the prize, this
appears to have been more of a publicity stunt; in reality, he could afford to
cover the loss. He later released a successor puzzle, which has proven far more
difficult and remains unsolved.
Quantum computers exploit superposition and entanglement to evaluate multiple
solutions in parallel. However, they do not simply evaluate all $n!$
permutations at once and automatically return the best one - an assumption that,
unfortunately, is still common. Once you measure the output of a quantum
algorithm, you effectively collapse the wavefunction, ending up with a single
measured state. Thus, careful algorithm design is required to boost the
probability of measuring the correct solution, often requiring many repeated
measurements. A relevant quantum algorithm in this context is Grover's
Algorithm, which offers a quadratic speedup in unstructured searches (e.g., from
$O(2^n)$ to $O(\sqrt{2^n})$). However, TSPs and other optimization problems have
enough internal structure in practice that classical approaches can exploit it,
often rendering Grover's quadratic speedup unimpressive by comparison.
Quantum computers also come with significant drawbacks relative to classical
computers. Their quantum state collapses upon measurement, preventing techniques
like "early abort" or classical branch-and-bound pruning, where large portions
of the search space can be discarded based on intermediate results. Classical
algorithms rely on this kind of dynamic pruning to speed up the search. Quantum
computing sacrifices flexibility for parallel evaluation—an advantage in
unstructured or purely guesswork-based problems, but most practical optimization
problems have exploitable structure. While there may be ways around these
limitations and, in theory, quantum computers are more powerful than classical
ones, whether this yields substantial real-world benefits for optimization
remains unclear.
In some sense, quantum computers face challenges reminiscent of GPU computing:
both process many data points in parallel (Single-Instruction, Multiple-Data),
but lose out on some flexibility since every thread must follow identical
instructions. Even for GPUs, applying them effectively to large-scale
optimization has proven tricky, though progress continues.
If you want more perspectives on the topic, the following articles may be of
interest:
- [Challenges and Opportunities in Quantum Optimization](https://arxiv.org/pdf/2312.02279):
This preprint gives on 72 pages an extensive and well-written overview of the
state of the art in quantum optimization. While the conclusion sounds quite
optimistic, the paper is very clear about the current limitations and
challenges. while it caters a scientific audience, it is still quite
accessible.
- [Understanding instance hardness for optimisation algorithms: Methodologies, open challenges and post-quantum implications](https://www.sciencedirect.com/science/article/pii/S0307904X2500040X):
This paper states that "it seems likely that there will be no quantum
advantage for the TSP" due to challenges in tuning the parameters of QUBOs to
even yield feasible solutions. However, it considers unconstrained
optimization problems such as the MAX-CUT to have a higher chance of
benefiting from quantum computing.
- [Disentangling Hype from Practicality: On Realistically Achieving Quantum Advantage](https://cacm.acm.org/research/disentangling-hype-from-practicality-on-realistically-achieving-quantum-advantage/#R3)
Gives strong arguments why it can be hard to achieve quantum advantage in
practice, especially why quadratic speedup algorithms like Grover's Algorithm
will not suffice.
- [Quantum advantage for NP approximation? For REAL this time?](https://scottaaronson.blog/?p=8375):
A blog post by Scott Aaronson, a well-known quantum computing expert, offering
a critical take on the QAOA algorithm and its claimed advantages.
- [Challenges and opportunities in quantum optimization](https://www.nature.com/articles/s42254-024-00770-9):
A balanced discussion by a group of researchers, highlighting potential
opportunities without making unfounded claims.
- [Quantum Annealing versus Digital Computing: An Experimental Comparison](https://www.researchgqate.net/publication/353155344_Quantum_Annealing_versus_Digital_Computing_An_Experimental_Comparison):
This paper compares quantum annealing to classical computing for optimization
problems and found no indication of a quantum advantage.
> [!WARNING]
>
> I do not claim to be an expert in quantum computing, so please interpret my
> remarks with appropriate caution. This book is an open-source project;
> therefore, if you have any corrections or suggestions to help improve the
> material for the community, feel free to open an issue or submit a pull
> request on [GitHub](https://github.com/d-krupke/cpsat-primer/).
## Benchmarking your Model
Benchmarking is an essential step if your model is not yet meeting the
performance standards of your application or if you are aiming for an academic
publication. This process involves analyzing your model's performance,
especially important if your model has adjustable parameters. Running your model
on a set of predefined instances (a benchmark) allows you to fine-tune these
parameters and compare results. Moreover, if alternative models exist,
benchmarking helps you ascertain whether your model truly outperforms these
competitors.
Designing an effective benchmark is a nuanced task that demands expertise. This
section aims to guide you in creating a reliable benchmark suitable for
publication purposes.
Given the breadth and complexity of benchmarking, our focus will be on the
basics, particularly through the lens of the Traveling Salesman Problem (TSP),
as previously discussed in the `add_circuit` section. We refer to the different
model implementations as 'solvers', and we'll explore four specific types:
- A solver employing the `add_circuit` approach.
- A solver based on the Miller-Tucker-Zemlin formulation.
- A solver utilizing the Dantzig-Fulkerson-Johnson formulation with iterative
addition of subtour constraints until a connected tour is achieved.
- A Gurobi-based solver applying the Dantzig-Fulkerson-Johnson formulation via
Lazy Constraints, which are not supported by CP-SAT.
This example highlights common challenges in benchmarking and strategies to
address them. A key obstacle in solving NP-hard problems is the variability in
solver performance across different instances. For instance, a solver might
easily handle a large instance but struggle with a smaller one, and vice versa.
Consequently, it is crucial to ensure that your benchmark encompasses a
representative variety of instances. This diversity is vital for drawing
meaningful conclusions, such as the maximum size of a TSP instance that can be
solved or the most effective solver to use.
For a comprehensive exploration of benchmarking, I highly recommend Catherine C.
McGeoch's book,
["A Guide to Experimental Algorithmics"](https://www.cambridge.org/core/books/guide-to-experimental-algorithmics/CDB0CB718F6250E0806C909E1D3D1082),
which offers an in-depth discussion on this topic.
### Distinguishing Exploratory and Workhorse Studies in Benchmarking
Before diving into comprehensive benchmarking, it is essential to conduct
preliminary investigations to assess your model’s capabilities and identify any
foundational issues. This phase, known as _exploratory studies_, is crucial for
establishing the basis for more detailed benchmarking, subsequently termed as
_workhorse studies_. These latter studies aim to provide reliable answers to
specific research questions and are often the core of academic publications. It
is important to explicitly differentiate between these two study types and
maintain their distinct purposes: exploratory studies for initial understanding
and flexibility, and workhorse studies for rigorous, reproducible research.
#### Exploratory Studies: Foundation Building
Exploratory studies serve as an introduction to both your model and the problem
it addresses. This phase is about gaining preliminary understanding and
insights.
- **Objective**: The goal here is to gather early insights rather than
definitive conclusions. This phase is instrumental in identifying realistic
problem sizes, potential challenges, and narrowing down hyperparameter search
spaces.
For instance, in the `add_circuit`-section, an exploratory study helped us
determine that our focus should be on instances with 100 to 200 nodes. If you
encounter fundamental issues with your model at this stage, it’s advisable to
address these before proceeding to workhorse studies.
> [!WARNING]
>
> Occasionally, the primary performance bottleneck in your model may not be
> CP-SAT but rather the Python segment where the model is being generated. In
> these instances, identifying the most resource-intensive parts of your Python
> code is crucial. I have found the profiler
> [Scalene](https://github.com/plasma-umass/scalene) to be well-suited to
> investigate and pinpoint these bottlenecks.
#### Workhorse Studies: Conducting In-depth Evaluations
Workhorse studies follow the exploratory phase, characterized by more structured
and meticulous approaches. This stage is vital for a comprehensive evaluation of
your model and collecting substantive data for analysis.
- **Objective**: These studies are designed to answer specific research
questions and provide meaningful insights. The approach here is more
methodical, focusing on clearly defined research questions. The benchmarks
designed should be well-structured and large enough to yield statistically
significant results.
Remember, the aim is not to create a flawless benchmark right away but to evolve
it as concrete questions emerge and as your understanding of the model and
problem deepens. These studies, unlike exploratory ones, will be the focus of
your scientific publications, with exploratory studies only referenced for
justifying certain design decisions.
> [!TIP]
>
> Use the
> [SIGPLAN Empirical Evaluation Checklist](https://raw.githubusercontent.com/SIGPLAN/empirical-evaluation/master/checklist/checklist.pdf)
> if your evaluation has to satisfy academic standards.
### Designing a Robust Benchmark for Effective Studies
When undertaking both exploratory and workhorse studies, the creation of a
well-designed benchmark is a critical step. This benchmark is the basis upon
which you'll test and evaluate your solvers. For exploratory studies, your
benchmark can start simple and progressively evolve. However, when it comes to
workhorse studies, the design of your benchmark demands meticulous attention to
ensure comprehensiveness and reliability.
While exploratory studies also benefit from a thoughtfully designed benchmark—as
it accelerates insight acquisition—the primary emphasis at this stage is to have
a functioning benchmark in place. This initial benchmark acts as a springboard,
providing a foundation for deeper, more detailed analysis in the subsequent
workhorse studies. The key is to balance the immediacy of starting with a
benchmark against the long-term goal of refining it for more rigorous
evaluations.
Ideally, a robust benchmark would consist of a large set of real-world
instances, closely reflecting the actual performance of your solver. Real-world
instances, however, are often limited in quantity and may not provide enough
data for a statistically significant benchmark. In such cases, it is advisable
to explore existing benchmarks from literature, like the
[TSPLIB](http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/) for TSP.
Leveraging established benchmarks allows for comparison with prior studies, but
be cautious about their quality, as not all are equally well-constructed. For
example, TSPLIB's limitations in terms of instance size variation and
heterogeneity can hinder result aggregation.
Therefore, creating custom instances might be necessary. When doing so, aim for
enough instances per size category to establish reliable and statistically
significant data points. For instance, generating 10 instances for each size
category (e.g., 25, 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500) can
provide a solid basis for analysis. This approach, though modest in scale,
suffices to illustrate the benchmarking process.
Exercise caution with random instance generators, as they may not accurately
represent real-world scenarios. For example, randomly generated TSP instances
might lack collinear points common in real-world situations, like houses aligned
on straight roads, or they might not replicate real-world clustering patterns.
To better mimic reality, incorporate real-world data or use diverse generation
methods to ensure a broader variety of instances. For the TSP, we could for
example also have sampled from the larger TSPLIB instances.
Consider conducting your evaluation using two distinct benchmarks, especially
when dealing with different data types. For instance, you might have one
benchmark derived from real-world data which, although highly relevant, is too
limited in size to provide robust statistical insights. Simultaneously, you
could use a second benchmark based on a larger set of random instances, better
suited for detailed statistical analysis. This dual-benchmark approach allows
you to demonstrate the consistency and reliability of your results, ensuring
they are not merely artifacts of a particular dataset's characteristics. It's a
strategy that adds depth to your evaluation, showcasing the robustness of your
findings across varied data sources. We will use this approach below, generating
robust plots from random instances, but also comparing them to real-world
instances. Mixing the two benchmarks would not be advisable, as the random
instances would dominate the results.
Lastly, always separate the creation of your benchmark from the execution of
experiments. Create and save instances in a separate process to minimize errors.
The goal is to make your evaluation as error-proof as possible, avoiding the
frustration and wasted effort of basing decisions on flawed data. Be
particularly cautious with pseudo-random number generators; while theoretically
deterministic, their use can inadvertently lead to irreproducible results.
Sharing benchmarks is also more straightforward when you can distribute the
instances themselves, rather than the code used to generate them.
### Efficiently Managing Your Benchmarks
Managing benchmark data can become complex, especially with multiple experiments
and research questions. Here are some strategies to keep things organized:
- **Folder Structure**: Maintain a clear folder structure for your experiments,
with a top-level `evaluations` folder and descriptive subfolders for each
experiment. For our experiment we have the following structure:
```
evaluations
├── tsp
│ ├── 2023-11-18_random_euclidean
│ │ ├── PRIVATE_DATA
│ │ │ ├── ... all data for debugging
│ │ ├── PUBLIC_DATA
│ │ │ ├── ... selected data to share
│ │ ├── README.md: Provide a short description of the experiment
│ │ ├── 00_generate_instances.py
│ │ ├── 01_run_experiments.py
│ │ ├── ....
│ ├── 2023-11-18_tsplib
│ │ ├── PRIVATE_DATA
│ │ │ ├── ... all data for debugging
│ │ ├── PUBLIC_DATA
│ │ │ ├── ... selected data to share
│ │ ├── README.md: Provide a short description of the experiment
│ │ ├── 01_run_experiments.py
│ │ ├── ....
```
- **Redundancy and Documentation**: While some redundancy is acceptable,
comprehensive documentation of each experiment is crucial for future
reference.
- **Simplified Results**: Keep a streamlined version of your results for easy
access, especially for plotting and sharing.
- **Data Storage**: Save all your data, even if it seems insignificant at the
time. This ensures you have a comprehensive dataset for later analysis or
unexpected inquiries. Because this can become a lot of data, it is advisable
to have two folders: One with all data and one with a selection of data that
you want to share.
- **Experiment Flexibility**: Design experiments to be interruptible and
extendable, allowing for easy resumption or modification. This is especially
important for exploratory studies, where you may need to make frequent
adjustments. However, if your workhorse study takes a long time to run, you do
not want to repeat it from scratch if you want to add a further solver.
- **Utilizing Technology**: Employ tools like slurm for efficient distribution
of experiments across computing clusters, saving time and resources. The
faster you have your results, the faster you can act on them.
Due to a lack of tools that exactly fitted my needs I developed
[AlgBench](https://github.com/d-krupke/AlgBench) to manage the results, and
[Slurminade](https://github.com/d-krupke/slurminade) to easily distribute the
experiments on a cluster via a simple decorator. However, there may be better
tools out there, now, especially from the Machine Learning community. Drop me a
quick mail if you have found some tools you are happy with, and I will take a
look myself.
### Analyzing the results
Let us now come to the actual analysis of the results. We will focus on the
following questions:
- Up to which size can we solve TSP instances with the different solvers?
- Which solver is the fastest?
- How does the performance change if we increase the optimality tolerance?
**Our Benchmarks:** We executed the four solvers with a time limit of 90s and
the optimality tolerances [0.1%, 1%, 5%, 10%, 25%] on a random benchmark set and
a TSPLIB benchmark set. The random benchmark set consists of 10 instances for
each number of nodes
`[25, 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500]`. The weights were
chosen based on randomly embedding the nodes into a 2D plane and using the
Euclidean distances. The TSPLIB benchmark consists of all Euclidean instances
with less than 500 nodes. It is critical to have a time limit, as otherwise, the
benchmarks would take forever. You can find all find the whole experiment
[here](https://github.com/d-krupke/cpsat-primer/blob/main/evaluations/tsp/).
Let us first look at the results of the random benchmark, as they are easier to
interpret. We will then compare them to the TSPLIB benchmark.
#### Random Instances
A common, yet simplistic method to assess a model's performance involves
plotting its runtime against the size of the instances it processes. However,
this approach can often lead to inaccurate interpretations, particularly because
time-limited cutoffs can disproportionately affect the results. Instead of the
expected exponential curves, you will get skewed sigmoidal curves. Consequently,
such plots might not provide a clear understanding of the instance sizes your
model is capable of handling efficiently.
|  |
| :-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| The runtimes are sigmoidal instead of exponential because the time limit skews the results. The runtime can frequently exceed the time limit, because of expensive model building, etc. Thus, a pure runtime plot says surprisingly little (or is misleading) and can usually be discarded. |
Instead of just cutting off the runtime, a common metric is PAR10, which sets
the runtime to 10 times the time limit if the solver does not finish within the
time limit, and will actually penalize timeouts. However, it still does not
solve the problem that we actually do not know the true runtime such that these
plots will always lie.
To gain a more accurate insight into the capacities of your model, consider
plotting the proportion of instances of a certain size that your model
successfully solves. This method requires a well-structured benchmark to yield
meaningful statistics for each data point. Without this structure, the resulting
curve may appear erratic, making it challenging to draw dependable conclusions.
|  |
| :--------------------------------------------------------------------------------------------------------------------------------------------------: |
| For each x-value: What are the chances (y-values) that a model of this size (x) can be solved? |
Furthermore, if the pursuit is not limited to optimal solutions but extends to
encompass solutions of acceptable quality, the analysis can be expanded. One can
plot the number of instances that the model solves within a defined optimality
tolerance, as demonstrated in the subsequent figure:
|  |
| :------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| For each x-value: What are the chances (y-values) that a model of this size (x) can be solved to what quality (line style)? |
For a comparative analysis across various models against an arbitrary benchmark,
cactus plots emerge as a potent tool. These plots illustrate the number of
instances solved over time, providing a clear depiction of a model's efficiency.
For example, a coordinate of $x=10, y=20$ on such a plot signifies that 20
instances were solved within a span of 10 seconds each. It is important to note,
however, that these plots do not facilitate predictions for any specific
instance unless the benchmark set is thoroughly familiar. They do allow for an
estimation of which model is quicker for simpler instances and which can handle
more challenging instances within a reasonable timeframe. The question of what
exactly is a simple or challenging instance, however, is better answered by the
previous plots.
Cactus plots are notably prevalent in the evaluation of SAT-solvers, where
instance size is a poor indicator of difficulty. A more detailed discussion on
this subject can be found in the referenced academic paper:
[Benchmarking Solvers, SAT-style by Brain, Davenport, and Griggio](http://www.sc-square.org/CSA/workshop2-papers/RP3-FinalVersion.pdf)
|  |
| :------------------------------------------------------------------------------------------------------------------------------------------: |
| For each x-value: How many (y) of the benchmark instances could have been solved with this time limit (x)? |
Additionally, the analysis can be refined to account for different quality
tolerances. This requires either multiple experimental runs or tracking the
progression of the lower and upper bounds within the solver. In the context of
CP-SAT, for instance, this tracking can be implemented via the Solution
Callback, although its activation is may depend on updates to the objective
rather than the bounds.
|  |
| :--------------------------------------------------------------------------------------------------------------------------------------------------: |
| For each x-value: How many (y) of the benchmark instances could have been solved to a specific quality (line style) with this time limit (x)? |
Instead of plotting the number of solved instances, one can also plot the number
of unsolved instances over time. This can be easier to read and additionally
indicates the number of instances in the benchmark. However, I personally do not
have a preference for one or the other, and would recommend using the one that
is more intuitive to read for you.
#### TSPLIB
Our second benchmark for the Traveling Salesman Problem leverages the TSPLIB, a
set of instances based on real-world data. This will introduce two challenges:
1. The difficulty in aggregating benchmark data due to its limited size and
heterogeneous nature.
2. Notable disparities in results, arising from the differing characteristics of
random and real-world instances.
The irregularity in instance sizes makes traditional plotting methods, like
plotting the number of solved instances over time, less effective. While data
smoothing methods, such as rolling averages, are available, they too have their
limitations.
|  |
| :-----------------------------------------------------------------------------------------------------------------------------------------: |
| Such a plot may prove inefficient when dealing with high variability, particularly when some data points are underrepresented. |
In contrast, the cactus plot still provides a clear and comprehensive
perspective of various model performances. An interesting observation we can
clearly see in it, is the diminished capability of the "Iterative Dantzig" model
in solving instances, and a closer performance alignment between the
`add_circuit` and Gurobi models.
|  |
| :------------------------------------------------------------------------------------------------------------------------------------------------: |
| Cactus plots maintain clarity and relevance, and show a performance differences between TSPLib and random instances. |
However, since cactus plots do not offer insights into individual instances, it
is beneficial to complement them with a detailed table of results for the
specific model you are focusing on. This approach ensures a more nuanced
understanding of model performance across varied instances. The following table
provides the results for the `add_circuit`-model.
| Instance | # nodes | runtime | lower bound | objective | opt. gap |
| :------- | ------: | ------: | ----------: | --------: | -------: |
| att48 | 48 | 0.47 | 33522 | 33522 | 0 |
| eil51 | 51 | 0.69 | 426 | 426 | 0 |
| st70 | 70 | 0.8 | 675 | 675 | 0 |
| eil76 | 76 | 2.49 | 538 | 538 | 0 |
| pr76 | 76 | 54.36 | 108159 | 108159 | 0 |
| kroD100 | 100 | 9.72 | 21294 | 21294 | 0 |
| kroC100 | 100 | 5.57 | 20749 | 20749 | 0 |
| kroB100 | 100 | 6.2 | 22141 | 22141 | 0 |
| kroE100 | 100 | 9.06 | 22049 | 22068 | 0 |
| kroA100 | 100 | 8.41 | 21282 | 21282 | 0 |
| eil101 | 101 | 2.24 | 629 | 629 | 0 |
| lin105 | 105 | 1.37 | 14379 | 14379 | 0 |
| pr107 | 107 | 1.2 | 44303 | 44303 | 0 |
| pr124 | 124 | 33.8 | 59009 | 59030 | 0 |
| pr136 | 136 | 35.98 | 96767 | 96861 | 0 |
| pr144 | 144 | 21.27 | 58534 | 58571 | 0 |
| kroB150 | 150 | 58.44 | 26130 | 26130 | 0 |
| kroA150 | 150 | 90.94 | 26498 | 26977 | 2% |
| pr152 | 152 | 15.28 | 73682 | 73682 | 0 |
| kroA200 | 200 | 90.99 | 29209 | 29459 | 1% |
| kroB200 | 200 | 31.69 | 29437 | 29437 | 0 |
| pr226 | 226 | 74.61 | 80369 | 80369 | 0 |
| gil262 | 262 | 91.58 | 2365 | 2416 | 2% |
| pr264 | 264 | 92.03 | 49121 | 49512 | 1% |
| pr299 | 299 | 92.18 | 47709 | 49217 | 3% |
| linhp318 | 318 | 92.45 | 41915 | 52032 | 19% |
| lin318 | 318 | 92.43 | 41915 | 52025 | 19% |
| pr439 | 439 | 94.22 | 105610 | 163452 | 35% |
A last option is to split the y-axis into the part where the solving time is
still within the time limit, and the part where it is not and the optimality gap
becomes relevant. Such a plot has some benefits but can also be difficult to
scale or aggregate.
|  |
| :--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| This plot splits the y-axis into a part where the instances can still be solved within the time limit, such that the time can be shown, and the part where the time limit is exceeded, such that the optimality gap can be shown. This example was generated by my student assistant Rouven Kniep, and he is working on creating an easy-to-use script for such plots. |
This should highlight that often you need a combination of different benchmarks
and plots to get a good understanding of the performance of your model.
### Comparing Production with Development Versions on Multiple Metrics
In applied benchmarking, a common task is evaluating whether the latest version
of your algorithm is actually better than the previous one, particularly when
you do not have a single, clear metric for comparison. Once your implementation
reaches a certain level of maturity, improving all aspects simultaneously
becomes challenging, and trade-offs are often necessary. Additionally, if
business requirements change, new constraints might be introduced that could
negatively impact some metrics, which managers may not fully understand. In such
cases, it is useful to directly compare how various metrics change between the
two versions.
One effective method for this comparison is using scatter plots, where the
x-axis represents the metric values from the old version, and the y-axis
represents the values from the new version. Points on the diagonal indicate
instances where nothing has changed, points above the diagonal show where the
metric increased, and points below the diagonal indicate a decrease. This visual
representation gives you a clear overview of where improvements have been made
and where performance has declined, highlighting the trade-offs involved. This
information can help you determine whether you are moving in the right
direction.
Scatter plots are particularly valuable when you cannot rely on a single metric
to compare the two versions but need to understand the overall impact of the
changes and the trade-offs made. The following figure shows an example from an
imaginary delivery optimization problem, where the new algorithm is able to
reduce the longest delivery tours but slightly degrades on the average tours of
a delivery schedule. Based on this data, you can then decide with the manager if
the trade-off is acceptable.
|  |
| :-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| These scatter plots illustrate how metrics change between two versions of an algorithm and where trade-offs are necessary. They also help identify outliers—for example, if you have generally improved but see a significant degradation for certain individual instances. However, this type of plot is most effective for comparing two versions and can become less readable if the differences between the versions are too substantial. Consider these as exploratory tools that reveal general trends. |
The code for this scatter plot is available
[here](https://raw.githubusercontent.com/d-krupke/cpsat-primer/main/examples/a_b_comparison/scatter_with_performance_zones.py).
### Conclusion
Benchmarking solvers for NP-hard problems is not as straightforward as it might
seem at first. There are many pitfalls and often there is no perfect solution.
On the example of the TSP, we have seen how we can still get some useful results
and nice plots on which we can base our decisions.
## Using CP-SAT for Bigger Problems with Large Neighborhood Search
CP-SAT is great at solving small and medium-sized problems. But what if you have
a really big problem on your hands? One option might be to use a special kind of
algorithm known as a "meta-heuristic", like a
[genetic algorithm](https://en.wikipedia.org/wiki/Genetic_algorithm). But these
can be hard to set up and might not even give you good results.
Sometimes you will see new algorithms with cool-sounding names in scientific
papers. While tempting, these are often just small twists on older methods and
might leave out key details that make them work. If you are interested, there's
a discussion about this issue in a paper by Sörensen, called
["Metaheuristics – The Metaphor Exposed"](http://onlinelibrary.wiley.com/doi/10.1111/itor.12001/).
The good news? You do not have to implement an algorithm that simulates the
mating behavior of forest frogs to solve your problem. If you already know how
to use CP-SAT, you can stick with it to solve big problems without adding
unnecessary complications. Even better? This technique, called Large
Neighborhood Search, often outperforms all other approaches.
### What Sets Large Neighborhood Search Apart?
Many traditional methods generate several "neighbor" options around an existing
solution and pick the best one. However, making each neighbor solution takes
time, limiting how many you can examine.
Large Neighborhood Search (LNS) offers a more efficient approach. Instead of
generating neighbors one by one, LNS formulates a "mini-problem" that modifies
parts of the current solution. This often involves randomly selecting some
variables, resetting them, and using CP-SAT (or a similar tool) to find the
optimal new values within the context of the remaining solution. This method,
known as "destroy and repair," allows for a broader exploration of neighbor
solutions without constructing each one individually.
Moreover, LNS can easily be mixed with other methods like genetic algorithms. If
you are already using a genetic algorithm, you could supercharge it by applying
CP-SAT to find the best possible crossover of two or more existing solutions. It
is like genetic engineering, but without any ethical worries!
When looking into the logs of CP-SAT, you may notice that it uses LNS itself to
find better solutions.
```
8 incomplete subsolvers: [feasibility_pump, graph_arc_lns, graph_cst_lns, graph_dec_lns, graph_var_lns, rins/rens, rnd_cst_lns, rnd_var_lns]
```
Why does it not suffice to just run CP-SAT if it already solves the problem with
LNS? The reason is that CP-SAT has to be relatively problem-agnostic. It has no
way of knowing the structure of your problem and thus cannot use this
information to improve the search. You on the other hand know a lot about your
problem and can use this knowledge to implement a more efficient version.
**Literature:**
- General Paper on LNS-variants:
[Pisinger and Ropke - 2010](https://backend.orbit.dtu.dk/ws/portalfiles/portal/5293785/Pisinger.pdf)
- A generic variant (RINS), that is also used by CP-SAT:
[Danna et al. 2005](https://link.springer.com/article/10.1007/s10107-004-0518-7)
We will now look into some examples to see this approach in action.
#### Example 1: Knapsack
You are given a knapsack that can carry a certain weight limit $C$, and you have
various items $I$ you can put into it. Each item $i\in I$ has a weight $w_i$ and
a value $v_i$. The goal is to pick items to maximize the total value while
staying within the weight limit.
```math
\max \sum_{i \in I} v_i x_i
```
```math
\text{s.t.} \sum_{i \in I} w_i x_i \leq C
```
```math
x_i \in \\{0,1\\}
```
This is one of the simplest NP-hard problems and can be solved with a dynamic
programming approach in pseudo-polynomial time. CP-SAT is also able to solve
many large instances of this problem in an instant. However, its simple
structure makes it a good example to demonstrate the use of Large Neighborhood
Search, even if the algorithm will not be of much use for this problem.
A simple idea for the LNS is to delete some elements from the current solution,
compute the remaining capacity after deletion, select some additional items from
the remaining items, and try to find the optimal solution to fill the remaining
capacity with the deleted items and the newly selected items. Repeat this until
you are happy with the solution quality. The number of items you delete and
select can be fixed such that the problem can be easily solved by CP-SAT. You
can find a full implementation under
[examples/lns_knapsack.ipynb](examples/lns_knapsack.ipynb).
Let us look only on an example here:
Instance: $C=151$,
$I=I_{0}(w=12, v=37),I_{1}(w=16, v=49),I_{2}(w=20, v=53),I_{3}(w=11, v=14),I_{4}(w=19, v=42),$
$\quad I_{5}(w=13, v=53),I_{6}(w=18, v=54),I_{7}(w=16, v=56),I_{8}(w=14, v=45),I_{9}(w=12, v=39),$
$\quad I_{10}(w=11, v=42),I_{11}(w=19, v=43),I_{12}(w=12, v=43),I_{13}(w=19, v=66),I_{14}(w=20, v=54),$
$\quad I_{15}(w=13, v=54),I_{16}(w=12, v=33),I_{17}(w=12, v=38),I_{18}(w=14, v=43),I_{19}(w=15, v=28),$
$\quad I_{20}(w=11, v=47),I_{21}(w=10, v=31),I_{22}(w=20, v=97),I_{23}(w=10, v=35),I_{24}(w=19, v=56),$
$\quad I_{25}(w=11, v=33),I_{26}(w=12, v=38),I_{27}(w=15, v=45),I_{28}(w=17, v=58),I_{29}(w=11, v=48),$
$\quad I_{30}(w=15, v=32),I_{31}(w=17, v=67),I_{32}(w=15, v=43),I_{33}(w=16, v=41),I_{34}(w=18, v=42),$
$\quad I_{35}(w=14, v=44),I_{36}(w=20, v=45),I_{37}(w=13, v=50),I_{38}(w=17, v=57),I_{39}(w=17, v=33),$
$\quad I_{40}(w=17, v=49),I_{41}(w=12, v=21),I_{42}(w=14, v=37),I_{43}(w=20, v=74),I_{44}(w=14, v=55),$
$\quad I_{45}(w=10, v=25),I_{46}(w=16, v=26),I_{47}(w=10, v=37),I_{48}(w=18, v=63),I_{49}(w=16, v=39),$
$\quad I_{50}(w=16, v=57),I_{51}(w=16, v=47),I_{52}(w=10, v=43),I_{53}(w=12, v=30),I_{54}(w=12, v=40),$
$\quad I_{55}(w=19, v=48),I_{56}(w=12, v=39),I_{57}(w=14, v=43),I_{58}(w=17, v=35),I_{59}(w=19, v=51),$
$\quad I_{60}(w=16, v=48),I_{61}(w=19, v=72),I_{62}(w=16, v=45),I_{63}(w=19, v=88),I_{64}(w=15, v=20),$
$\quad I_{65}(w=17, v=49),I_{66}(w=14, v=40),I_{67}(w=14, v=27),I_{68}(w=19, v=51),I_{69}(w=10, v=37),$
$\quad I_{70}(w=15, v=42),I_{71}(w=13, v=29),I_{72}(w=20, v=87),I_{73}(w=13, v=28),I_{74}(w=15, v=38),$
$\quad I_{75}(w=19, v=77),I_{76}(w=13, v=35),I_{77}(w=17, v=55),I_{78}(w=13, v=39),I_{79}(w=10, v=26),$
$\quad I_{80}(w=15, v=32),I_{81}(w=12, v=40),I_{82}(w=11, v=21),I_{83}(w=18, v=82),I_{84}(w=13, v=41),$
$\quad I_{85}(w=12, v=27),I_{86}(w=15, v=35),I_{87}(w=18, v=48),I_{88}(w=15, v=64),I_{89}(w=19, v=62),$
$\quad I_{90}(w=20, v=64),I_{91}(w=13, v=45),I_{92}(w=19, v=64),I_{93}(w=18, v=83),I_{94}(w=11, v=38),$
$\quad I_{95}(w=10, v=30),I_{96}(w=18, v=65),I_{97}(w=19, v=56),I_{98}(w=12, v=41),I_{99}(w=17, v=36)$
Initial solution of value 442:
$\\{I_{0}, I_{1}, I_{2}, I_{3}, I_{4}, I_{5}, I_{6}, I_{7}, I_{8}, I_{9}\\}$
We will now repeatedly delete 5 items from the current solution and try to fill
the newly gained capacity with an optimal solution built from the deleted items
and 10 additional items. Note that this approach essentially considers
$2^{5+10}=32768$ neighbored solutions in each iteration. However, we could
easily scale it up to consider $2^{100+900}\sim 10^{300}$ neighbored solutions
in each iteration thanks to the implicit representation of the neighbored
solutions and CP-SAT ability to prune large parts of the search space.
**Round 1 of LNS algorithm:**
- Deleting the following 5 items from the solution:
$\\{I_{0}, I_{7}, I_{8}, I_{9}, I_{6}\\}$
- Repairing solution by considering the following subproblem:
- Subproblem: $C=72$,
$I=\\{I_{6},I_{9},I_{86},I_{13},I_{47},I_{73},I_{0},I_{8},I_{7},I_{38},I_{57},I_{11},I_{60},I_{14}\\}$
- Computed the following solution of value 244 for the subproblem:
$\\{I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\\}$
- Combining
$\\{I_{1}, I_{2}, I_{3}, I_{4}, I_{5}\\}\cup \\{I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\\}$
- New solution of value 455:
$\\{I_{1}, I_{2}, I_{3}, I_{4}, I_{5}, I_{8}, I_{9}, I_{13}, I_{38}, I_{47}\\}$
**Round 2 of LNS algorithm:**
- Deleting the following 5 items from the solution:
$\\{I_{3}, I_{13}, I_{2}, I_{9}, I_{1}\\}$
- Repairing solution by considering the following subproblem:
- Subproblem: $C=78$,
$I=\\{I_{13},I_{9},I_{84},I_{41},I_{15},I_{42},I_{74},I_{16},I_{3},I_{1},I_{2},I_{67},I_{50},I_{89},I_{43}\\}$
- Computed the following solution of value 275 for the subproblem:
$\\{I_{1}, I_{15}, I_{43}, I_{50}, I_{84}\\}$
- Combining
$\\{I_{4}, I_{5}, I_{8}, I_{38}, I_{47}\\}\cup \\{I_{1}, I_{15}, I_{43}, I_{50}, I_{84}\\}$
- New solution of value 509:
$\\{I_{1}, I_{4}, I_{5}, I_{8}, I_{15}, I_{38}, I_{43}, I_{47}, I_{50}, I_{84}\\}$
**Round 3 of LNS algorithm:**
- Deleting the following 5 items from the solution:
$\\{I_{8}, I_{43}, I_{84}, I_{1}, I_{50}\\}$
- Repairing solution by considering the following subproblem:
- Subproblem: $C=79$,
$I=\\{I_{84},I_{76},I_{34},I_{16},I_{37},I_{20},I_{8},I_{43},I_{50},I_{1},I_{12},I_{35},I_{53}\\}$
- Computed the following solution of value 283 for the subproblem:
$\\{I_{8}, I_{12}, I_{20}, I_{37}, I_{50}, I_{84}\\}$
- Combining
$\\{I_{4}, I_{5}, I_{15}, I_{38}, I_{47}\\}\cup \\{I_{8}, I_{12}, I_{20}, I_{37}, I_{50}, I_{84}\\}$
- New solution of value 526:
$\\{I_{4}, I_{5}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{38}, I_{47}, I_{50}, I_{84}\\}$
**Round 4 of LNS algorithm:**
- Deleting the following 5 items from the solution:
$\\{I_{37}, I_{4}, I_{20}, I_{5}, I_{15}\\}$
- Repairing solution by considering the following subproblem:
- Subproblem: $C=69$,
$I=\\{I_{37},I_{4},I_{20},I_{15},I_{82},I_{41},I_{56},I_{76},I_{85},I_{5},I_{32},I_{57},I_{7},I_{67}\\}$
- Computed the following solution of value 260 for the subproblem:
$\\{I_{5}, I_{7}, I_{15}, I_{20}, I_{37}\\}$
- Combining
$\\{I_{8}, I_{12}, I_{38}, I_{47}, I_{50}, I_{84}\\}\cup \\{I_{5}, I_{7}, I_{15}, I_{20}, I_{37}\\}$
- New solution of value 540:
$\\{I_{5}, I_{7}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{38}, I_{47}, I_{50}, I_{84}\\}$
**Round 5 of LNS algorithm:**
- Deleting the following 5 items from the solution:
$\\{I_{38}, I_{12}, I_{20}, I_{47}, I_{37}\\}$
- Repairing solution by considering the following subproblem:
- Subproblem: $C=66$,
$I=\\{I_{20},I_{47},I_{37},I_{86},I_{58},I_{56},I_{54},I_{38},I_{12},I_{39},I_{68},I_{75},I_{66},I_{2},I_{99}\\}$
- Computed the following solution of value 254 for the subproblem:
$\\{I_{12}, I_{20}, I_{37}, I_{47}, I_{75}\\}$
- Combining
$\\{I_{5}, I_{7}, I_{8}, I_{15}, I_{50}, I_{84}\\}\cup \\{I_{12}, I_{20}, I_{37}, I_{47}, I_{75}\\}$
- New solution of value 560:
$\\{I_{5}, I_{7}, I_{8}, I_{12}, I_{15}, I_{20}, I_{37}, I_{47}, I_{50}, I_{75}, I_{84}\\}$
#### Example 2: Different Neighborhoods for the Traveling Salesman Problem
Simply removing a portion of the solution and then trying to fix it is not the
most effective approach. In this section, we will explore various neighborhoods
for the Traveling Salesman Problem (TSP). The geometry of TSP not only permits
advantageous neighborhoods but also offers visually appealing representations.
When you have several neighborhood strategies, they can be dynamically
integrated using an Adaptive Large Neighborhood Search (ALNS).
The image illustrates an optimization process for a tour that needs to traverse
the green areas, factoring in turn costs, within an embedded graph (mesh). The
optimization involves choosing specific regions (highlighted in red) and
calculating the optimal tour within them. As iterations progress, the initial
tour generally improves, although some iterations may not yield any enhancement.
Regions in red are selected due to the high cost of the tour within them. Once
optimized, the center of that region is added to a tabu list, preventing it from
being chosen again.
|  |
| :-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| Large Neighbordhood Search for Coverage Path Planning by repeatedly selecting a geometric region (red) and optimizing the tour within it. The red parts of the tour highlight the changes in the iteration. Read from left to right, and from up to down. |
How can you determine the appropriate size of a region to select? You have two
main options: conduct preliminary experiments or adjust the size adaptively
during the search. Simply allocate a time limit for each iteration. If the
solver does not optimize within that timeframe, decrease the region size.
Conversely, if it does, increase the size. Utilizing exponential factors will
help the size swiftly converge to its optimal dimension. However, it's essential
to note that this method assumes subproblems are of comparable difficulty and
may necessitate additional conditions.
For the Euclidean TSP, as opposed to a mesh, optimizing regions is not
straightforward. Multiple effective strategies exist, such as employing a
segment from the previous tour rather than a geometric region. By implementing
various neighborhoods and evaluating their success rates, you can allocate a
higher selection probability to the top-performing ones. This approach is
demonstrated in an animation crafted by two of my students, Gabriel Gehrke and
Laurenz Illner. They incorporated four distinct neighborhoods and utilized ALNS
to dynamically select the most effective one.
|  |
| :---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| Animation of an Adaptive Large Neighborhood Search for the classical Traveling Salesman Problem. It uses four different neighborhood strategies which are selected randomly with a probability based on their success rate in previous iterations. If you check the logs of the latest (v9.8) version of CP-SAT, it also rates the performance of its LNS-strategies and uses the best performing strategies more often (UCB1-algorithm). |
#### Multi-Armed Bandit: Exploration vs. Exploitation
Having multiple strategies for each iteration of your Large Neighborhood Search
(LNS) is beneficial, but how do you decide which one to use? While you could
select a strategy at random, this approach is inefficient because it is unlikely
to choose the best one. Alternatively, you could stick to the strategy that
performed well in the past, but there may be a better option you have not tried
yet. This brings us to the classic exploration vs. exploitation dilemma. On one
hand, you want to exploit strategies that have proven successful, but on the
other, you need to explore new strategies to discover potentially better ones.
Fortunately, this issue has been widely studied as the
[Multi-Armed Bandit Problem](https://en.wikipedia.org/wiki/Multi-armed_bandit),
and there are numerous effective solutions available. One popular approach is
the Upper Confidence Bound (UCB1) algorithm. I wanted to highlight this dilemma
to make you aware that many experts have already tackled it and developed
sophisticated strategies.
In practice, CP-SAT schedules its LNS strategies using a simple round-robin
method, as reflected by their equal number of calls in the logs. Whenever a
worker thread finishes its work, it will execute an iteration with the next
strategy in the list, leading to a fair distribution of calls. In this case, we
can see that the `'routing_path_lns'` strategy was the most successful,
improving the incumbent solution 41 times out of 65 calls. There might be room
for performance improvements by employing a more advanced strategy selection
algorithm. However, it is important to recognize the relatively low number of
calls to each strategy in combination with diminishing and noisy returns. If you
only have a few iterations, a more advanced algorithm may not have enough data
to make reliable decisions.
```
LNS stats Improv/Calls Closed Difficulty TimeLimit
'graph_arc_lns': 5/65 49% 0.26 0.10
'graph_cst_lns': 4/65 54% 0.47 0.10
'graph_dec_lns': 3/65 49% 0.26 0.10
'graph_var_lns': 4/66 55% 0.56 0.10
'rins/rens': 23/66 39% 0.03 0.10
'rnd_cst_lns': 12/66 50% 0.19 0.10
'rnd_var_lns': 6/66 52% 0.36 0.10
'routing_path_lns': 41/65 48% 0.10 0.10
'routing_random_lns': 24/65 52% 0.26 0.10
```