Data

Tools

Indexes

Applications

Experiments

Awesome

An open API service indexing awesome lists of open source software.

https://github.com/devinterview-io/decision-tree-interview-questions

🟣 Decision Tree interview questions and answers to help you prepare for your next machine learning and data science interview in 2024.
https://github.com/devinterview-io/decision-tree-interview-questions

ai-interview-questions coding-interview-questions coding-interviews data-science data-science-interview data-science-interview-questions data-scientist-interview decision-tree decision-tree-interview-questions decision-tree-questions decision-tree-tech-interview interview-practice interview-preparation machine-learning machine-learning-and-data-science machine-learning-interview machine-learning-interview-questions software-engineer-interview technical-interview-questions

Last synced: 3 months ago
JSON representation

🟣 Decision Tree interview questions and answers to help you prepare for your next machine learning and data science interview in 2024.

Awesome Lists containing this project

README 

        
# 60 Must-Know Decision Tree Interview Questions









machine-learning-and-data-science






#### You can also find all 60 answers here 👉 [Devinterview.io - Decision Tree](https://devinterview.io/questions/machine-learning-and-data-science/decision-tree-interview-questions)







## 1. What is a _Decision Tree_ in the context of _Machine Learning_?



A **Decision Tree** is a fundamental classification and regression algorithm in machine learning. It partitions the feature space into **distinctive subspaces** using a tree structure defined by binary, categorical-splits.



### Key Components



- **Root Node**: Represents the entire dataset. It indicates the starting point for building the tree.

- **Internal Nodes**: Generated to guide data to different branches. Each node applies a condition to separate the data.

- **Leaves/Decision Nodes**: Terminal nodes where the final decision is made.



### Building the Tree



- **Partitioning**: Data is actively stratified based on feature conditions present in each node.

- **Recursive Process**: Splitting happens iteratively, beginning from the root and advancing through the tree.



### Splitting Methods



- **Gini Impurity**: Measures how often the selected class would be mislabeled.

- **Information Gain**: Calculates the reduction in entropy after data is split. It selects the feature that provides the most gain.

- **Reduction in Variance**: Used in regression trees, it determines the variance reduction as a consequence of implementing a feature split.



### Strengths of Decision Trees



- **Interpretable**: Easily comprehended, requiring no preprocessing like feature scaling.

- **Handles Non-Linearity**: Suitable for data that doesn't adhere to linear characteristics.

- **Efficient with Multicollinearity and Irrelevant Features**: Their performance does not significantly deteriorate when presented with redundant or unimportant predictors.



### Limitations



- **Overfitting Sensitivity**: Prone to creating overly complex trees. Regularization techniques, like limiting the maximal depth, can alleviate this issue.

- **High Variance**: Decision trees are often influenced by the specific training data. Ensembling methods such as Random Forests can mitigate this.

- **Unbalanced Datasets**: Trees are biased toward the majority class, which is problematic for imbalanced categories.



### Code Example: Decision Tree Classifier



Here is the Python code:



```python

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import train_test_split

from sklearn.metrics import accuracy_score



# Load dataset (e.g., Iris)

# X = features, y = target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)



# Define the model

model = DecisionTreeClassifier()



# Fit the model

model.fit(X_train, y_train)



# Make predictions

y_pred = model.predict(X_test)



# Evaluate accuracy

accuracy = accuracy_score(y_test, y_pred)

print(f"Accuracy: {accuracy:.2f}")

```





## 2. Can you explain how a _Decision Tree_ is constructed?



The **decision tree** uses a top-down, recursive strategy. The tree begins with a single node that evaluates the entire dataset. Each parent node then "decides" the best way to split the data. The process repeats until the nodes or subsets are **pure** — secured under a single class or meet halting conditions.



### Key Concepts



- **Entropy**: A measure of impurity in a set of labels. Decision trees aim to reduce entropy by split.

- **Information Gain**: The entropy reduction achieved by a data split. The attribute yielding the highest gain is typically chosen.

- **Gini Index**: Another measure of impurity, similar to entropy, which decision trees can use instead.

- **Leaf Node**: A node at the end of the tree that doesn't split the data any further. All samples reaching a leaf belong to the same target class.



### Code Example: Using Entropy for Information Gain



Here is the Python code:



```python

from math import log2



# Calculate the entropy of a dataset

def calculate_entropy(data):

    total_count = len(data)

    label_counts = {}

    for row in data:

        label = row[-1]

        if label not in label_counts:

            label_counts[label] = 0

        label_counts[label] += 1

    entropy = 0

    for count in label_counts.values():

        probability = count / total_count

        entropy -= probability * log2(probability)

    return entropy



# Calculate information gain for a feature in a dataset

def calculate_information_gain(data, feature_index):

    entropy_before_split = calculate_entropy(data)

    unique_values = set(row[feature_index] for row in data)

    entropy_after_split = 0

    for value in unique_values:

        subset = [row for row in data if row[feature_index] == value]

        subset_entropy = calculate_entropy(subset)

        weight = len(subset) / len(data)

        entropy_after_split += weight * subset_entropy

    return entropy_before_split - entropy_after_split



# Example usage

data = [['Sunny', 85, 85, False, 'No'],

        ['Sunny', 80, 90, True, 'No'],

        ['Overcast', 83, 86, False, 'Yes'],

        ['Rainy', 70, 96, False, 'Yes'],

        ['Rainy', 68, 80, False, 'Yes']]

ig = calculate_information_gain(data, 0)  # Calculate IG for the first feature (Outlook)

print(ig)

```





## 3. What is the difference between _classification_ and _regression Decision Trees_?



**Decision Trees** serve various **machine learning** tasks. Here, we'll differentiate between their use for **classification** and **regression**.



#### Visual Representation



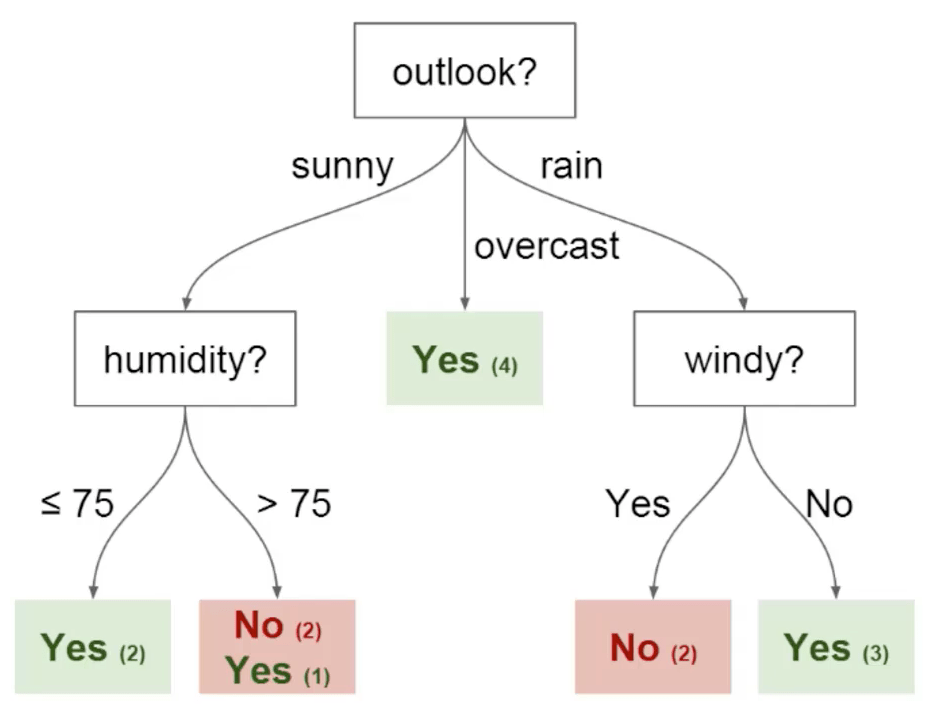
![Decision Tree for Classification](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/decision-trees%2Fdecision-tree-classification-min.png?alt=media&token=2dfb77c5-44bf-4e71-a797-6c91d88bb1cd)



### Classification Decision Trees



**Classifcation Decision Trees** are primarily employed for tasks with **discrete target variables**. They're especially useful for rapidly separating data into distinctive, non-overlapping categories.



#### Example



A company uses a Decision Tree to identify customer segments as "high-potential" and "low-interest."



#### Key Metrics



- **Gini Index**: Focuses on optimizing splits by reducing class impurity.

- **Information Gain**: Measures the extent of reduction in entropy after the dataset is split.



#### Code Example: Classification Decision Tree



Here is the Python code:



```python

from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier()

tree_clf.fit(X, y)

```



### Regression Decision Trees



Unlike their classification counterparts, **Regression Decision Trees** are best suited for **continuous target variables** and function by defining prediction points based on a unique set of features.



#### Example:



A real-estate firm might use a Decision Tree to estimate a property's sale price.



#### Key Metrics:



- **Variance Reduction**: Quantifies the drop in variance achieved following a dataset split.

- **Mean-Squared Error (MSE)**: Measures the average squared difference between the predicted values and the actual values.



#### Code Example: Regression Decision Tree



Here is the Python code:



```python

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor()

tree_reg.fit(X, y)

```





## 4. Name and describe the common _algorithms_ used to build a _Decision Tree_.



Several algorithms are designed for constructing **Decision Trees**. 



Let's look at four popular ones:



### Common Decision Tree Algorithms



#### ID3 (Iterative Dichotomiser 3) and its variations like C4.5 and C5.0.

  

- **Splitting Criterion**: Uses information gain or gain ratio as a base, which can lead to biases towards features with more unique categories.

- **Handling Missing Data**: Not natively supported.

- **Numerical Data Handling**: Suitable for attribute-values on a discrete domain (requiring categorical data).



#### CART (Classification and Regression Trees)



- **Splitting Criterion**: Employs Gini impurity or information gain.

- **Handling Missing Data**: It is possible, and typically the algorithm decides where to classify observations where data is missing.

- **Numerical Data Handling**: Binary recursive splitting based on whether a logical test, e.g., 'feature < 6', is met.



#### CHAID (Chi-square Automatic Interaction Detection)



- **Splitting Criterion**: Utilizes the chi-square statistic to detect interactions between variables and resulting multi-way splits for categorical predictors.

- **Handling Missing Data**: Able to operate with missing fields.

- **Numerical Data Handling**: Primarily for categorical data, but ordinal variables (both discrete and continuous) can also be utilized.



#### MARS (Multivariate Adaptive Regression Splines)



- **Splitting Criterion**: Employs the sum of least squares (SLS) as the primary method to minimize error for a continuous target variable.

- **Handling Missing Data**:  Offers options like surrogate split points to handle missing data.

- **Numerical Data Handling**:  Designed particularly for smooth, piecewise polynomial functions but can be extended and modified to account for categorical predictors.





## 5. What are the main _advantages_ of using _Decision Trees_?



**Decision Trees** are dynamic, versatile algorithms with several distinct advantages:



- **User-Friendly Nature**: They are intuitively understood and require little data preparation, making them a go-to choice for exploratory modeling.



- **Support for Both Numerical and Categorical Input**: This feature simplifies both data preparation and interpretation.



- **Efficiency in Time and Space**: Decision Trees are among the fastest algorithms, which is an advantage on big data.



- **Interpretability**: Their **transparent nature** allows both analysts and regulatory officers to understand the decision-making process.



- **Robustness Against Outliers and Missing Values**: Decision Trees can handle these issues without external treatment.



- **Feature Importance**: By calculating attribute metrics such as Gini impurity or information gain, Decision Trees highlight the most salient features, aiding in interpretability and feature selection.



- **Tree Pruning for Enhanced Generalization**: Techniques like Reduced Error Pruning or Cost-Complexity Pruning refine Decision Trees, mitigating overfitting and fostering better predictive accuracy.



- **Model Transparency**: Decision Trees are especially effective for generating white-box models, making their decisions clear and easy to follow, ensuring explainability and auditability for sensitive applications.



- **Combining Models with Ensemble Methods**: Decision trees can be aggregated into advanced models such as Random Forests, Gradient Boosted Trees, XGBoost, AdaBoost for even better performance.



- **Risk Assessment and Classification**: Decision Trees can be used to stratify risk in scenarios like healthcare, financial evaluations, or predictive maintenance.



- **Visual Representation**: Graphical summaries of the decision logic make them a powerful tool for data analysis and presentation.





## 6. Outline some _limitations_ or _disadvantages_ of _Decision Trees_.



While Decision Trees have several advantages, they also come with a set of limitations and challenges.



### Common Limitations



1. **Overfitting**: Unrestrained, decision trees can perfectly fit training data, leading to poor generalization. Techniques like pruning or using ensemble methods mitigate this.



2. **Bias Toward Dominant Classes**: In datasets with imbalanced class distribution, these trees tend to favor majority classes, which can lead to classification errors for the minority classes.



3. **Sensitive to Noise**: Even small amounts of noise can create a high level of complexity, leading to spurious predictions. Preprocessing techniques, such as data cleaning, can help here.



4. **Non-robust Splitting**: The choice of the "best" attribute to split on can vary significantly with minor changes in the dataset. Multiple trees through ensemble methods can help in this regard.



5. **Not Suitable for Non-binary Outcomes**: While extensions exist, traditional decision trees handle classification problems with only binary outcomes.



6. **Feature Correlation Handling**: Traditional decision trees can miss identifying correlated features that could be strong predictors in combination. Ensuring acyclic graphs can alleviate this.



7. **Data Partitioning Challenges**: Decision trees can struggle with segments containing data points with similar characteristics.  



   For example, in a two-dimensional feature space, a decision tree might create a partition that is suboptimal when considering both feature axes simultaneously.



8. **Subjectivity to Splits and Metrics**: The process of determining which attribute to split on (feature selection) and the best split point (threshold selection) might lead to subjectivity, especially when using Gini impurity or information gain metrics.



### Ways to Improve Decision Trees



To mitigate these challenges, various techniques and advanced versions of decision trees are available. Some of these include:



1. **Ensemble Methods**: Techniques like Random Forests or Boosting build multiple trees and aggregate their predictions, providing improved robustness, generalization, and accuracy.



2. **Feature Scaling and Selection**: Standardizing features to a common scale and identifying the most relevant ones can enhance tree performance.



3. **Pruning**: Limiting tree depth post-construction or removing nodes that do not improve overall tree performance helps to avoid overfitting.



4. **Dealing with Imbalanced Data**: Techniques like SMOTE (Synthetic Minority Over-sampling Technique) or using specialized ensemble approaches like Balanced Random Forests, are designed to handle imbalanced datasets.



5. **Cross-Validation**: Assessing tree performance on unseen data by splitting the dataset into multiple folds aids in understanding generalization errors.



6. **Cost-Complexity Pruning**: A variant of traditional pruning that considers the cost (usually misclassification costs) associated with subtrees, leading to better models.



7. **Use of Other Tree Models**: Enhanced decision tree models like C4.5 (which also handles non-binary outcomes) or CART have been developed to build on the shortcomings of earlier models.





## 7. Explain the concept of "_impurity_" in a _Decision Tree_ and how it's used.



While building a **Decision Tree**, the algorithm selects the feature that best splits the dataset at each node. This selection is based on minimizing the impurity or maximizing the information gain.



### What is Impurity?



**Impurity** quantifies the degree of "mixing" of classes within a dataset or a subset. In classification, impurity helps measure the **homogeneity** of a set of labels:



- A dataset is **pure** if it contains only one class or label.

- A dataset is **impure** if it contains an even mixture of classes.



Common impurity metrics in Decision Trees include:



1. **Gini Impurity**: Measures the probability of misclassifying an instance by randomly assigning a label according to the class distribution. It is in the range of $[0, 0.5]$.

  

  $$ G = 1 - \sum_{i=1}^{n} p_i^2 $$



2. **Entropy**: Reflects the amount of disorder in a system. It is mathematically similar to Gini impurity and also ranges from 0 (pure) to 1 (impure).



  $$ H = - \sum_{i=1}^{n} p_i \log(p_i) $$



3. **Misclassification Error**: Represents the proportion of majority-class data points, predicting the majority class for all instances. This metric is in the range $[0, 0.5]$.



  $$ E = 1 - \max(p_1, p_2, \ldots, p_n) $$



### Code Example



Here is the Python code:



```python

import numpy as np



# Gini impurity

def gini(p):

    return 1 - np.sum(p**2)



# Entropy

def entropy(p):

    return -np.sum(p * np.log(p))



# Misclassification error

def misclassification_error(p):

    return 1 - max(p)



# Class probabilities

p = np.array([0.4, 0.6])



# Calculate impurity measures

gini_impurity = gini(p)

entropy_impurity = entropy(p)

misclassification_error_impurity = misclassification_error(p)



print("Gini Impurity:", gini_impurity)

print("Entropy:", entropy_impurity)

print("Misclassification Error:", misclassification_error_impurity)

```





## 8. What are _entropy_ and _information gain_ in _Decision Tree_ context?



In the context of **Decision Trees**, **entropy** and **information gain** are key concepts used to measure the effectiveness of splitting a dataset.



### Entropy: Measure of Impurity



Kullback-Leibler divergence, $H(p)$, provides a principled approach to measuring information or surprise in datasets.



In the context of decision trees, we often compute the entropy, **$H(S)$**, for a given dataset **$S$** characterized by two classes (e.g., "yes"/"no", "spam"/"not spam"):



$$

H(S) = -p \log_2(p) - (1-p) \log_2(1-p)

$$



where $p$ is the probability of one class in the dataset.



### Information Gain: Decision Tree Metric



Information gain **(IG)** represents the reduction in entropy or uncertainty after a dataset is split by the attribute **$A$**:



$$

IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)

$$



where $S_v$ is the subset of **$S$** for which attribute **$A$** has value **$v$**.



Lower entropy values and higher information gain values translate to more effective, rule-based dataset partitions in decision trees.





## 9. Define _Gini impurity_ and its role in _Decision Trees_.



**Gini impurity** is a metric used in **Decision Trees** to evaluate the "purity" of a split.



### Role in Decision Trees



The Gini impurity is employed at each split point in a decision tree to determine which feature and split value to use. The goal is to find the split that minimizes the impurity by **maximizing the information gain**.



### Gini Impurity Equation



$$

\text{Gini}(p) = 1 - \sum_{i=1}^J p(i)^2

$$



where:

- $J$ is the number of target classes.

- $p(i)$ represents the probability of a randomly selected sample being correctly classified as class $i$.



### Gini Calculation Steps



1. **Squaring Probabilities**: Square the probabilities of each class.

2. **Summation**: Sum the squared probabilities.

3. **Subtraction**: Subtract the result from 1.



### Advantages of Gini Impurity



- **Computationally Efficient**: Gini impurity does not require the expensive computation of logarithms, making it faster to calculate than other impurity measures such as entropy.

- **Interpretability**: The resulting Gini score has a direct, intuitive meaning and is easier to interpret in the context of decision trees.



### Example: Gini Impurity Calculation



Suppose a node has 25 samples, 10 of class A and 15 of class B:



$$

$$

\text{Probability}(\text{Class A}) &= \frac{10}{25} = 0.4 \\

\text{Probability}(\text{Class B}) &= \frac{15}{25} = 0.6

$$

$$



Using these probabilities:



$$

$$

\text{Gini Impurity} &= 1 - \left(\left(0.4\right)^2 + \left(0.6\right)^2\right) \\

&= 1 - \left(0.16 + 0.36\right) \\

&= 1 - 0.52 \\

&= 0.48

$$

$$



So the Gini impurity of this node is **0.48**.





## 10. Discuss how _Decision Trees_ handle both _categorical_ and _numerical data_.



**Decision Trees** are versatile classifiers that can effectively handle both **categorical** and **numerical data**. Techniques for processing these data types include Gini impurity, Information Gain, and the use of binary splits.



### Gini Impurity and Information Gain



1. **Gini Impurity**:

   - For categorical variables: This measures misclassification when more than two categories are present. Categories are directly used for calculating the impurity.

   - For numerical variables: It handles binary classification by converting the numerical value into a binary outcome (e.g., "above" or "below" a certain threshold) and then calculates impurity as if it were a binary categorical variable.



2. **Information Gain**:

   - For categorical variables: Evaluates reduction in entropy or information uncertainty after particular categorizations.

   - For numerical variables: Uses a binary split to convert the numerical variable into a two-way categorical variable. It's commonly applied using the **Gini index** in binary mode, whereby the point yielding the highest information gain is chosen as the splitting point.



### Binary Splits



- **Categorical Data**: Each distinct category represents a unique branch under a parent node. A data point enters the branch corresponding to its category.

  

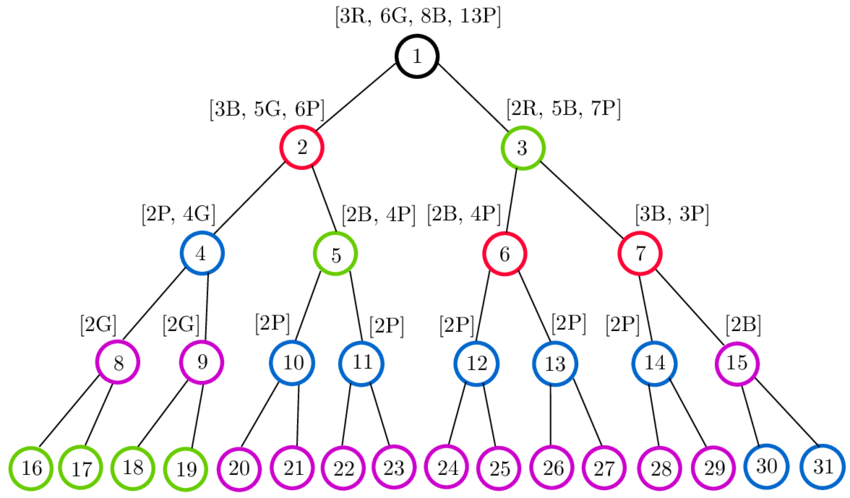
![Binary Splits Color](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/decision-trees%2Fcolor-splitting-algorithm.png?alt=media&token=299a1356-b752-49c2-9d53-a852a333eff4)



- **Numerical Data**: Uses binary splits to convert continuous numerical values into ordered categories. The benefit of binary splitting is that only two new branches are created at each node, which simplifies decision-making and visualization.



![Binary Splits Numbers](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/decision-trees%2Fsplits-numerical.svg?alt=media&token=659479d8-8ea5-4cc6-8239-3feb00e310b1)



### Coding Example: Numerical vs Categorical Data Splits

Here is the Python code: 



```python

from sklearn.tree import DecisionTreeClassifier

import pandas as pd



# Sample dataset incorporating both numerical and categorical features

data = {

    'Salary': [50000, 80000, 30000, 70000, 62000],  # Numerical

    'Education': ['Bachelors', 'Masters', 'High School', 'PhD', 'Masters'],  # Categorical

    'Employed': ['Yes', 'Yes', 'No', 'No', 'Yes']  # Categorical

}



# Converting to DataFrame for easier handling

df = pd.DataFrame(data)



# Creating the Decision Tree classifier

tree_clf = DecisionTreeClassifier()



# Fitting the classifier to the dataset

tree_clf.fit(df, ['Yes', 'No', 'No', 'Yes', 'Yes'])

```





## 11. What is _tree pruning_ and why is it important?



**Tree pruning** involves the removal of non-essential branches to streamline and optimize decision trees. This optimization is crucial in reducing overfitting and resource demands, while improving model generalization.



### Visual Representation



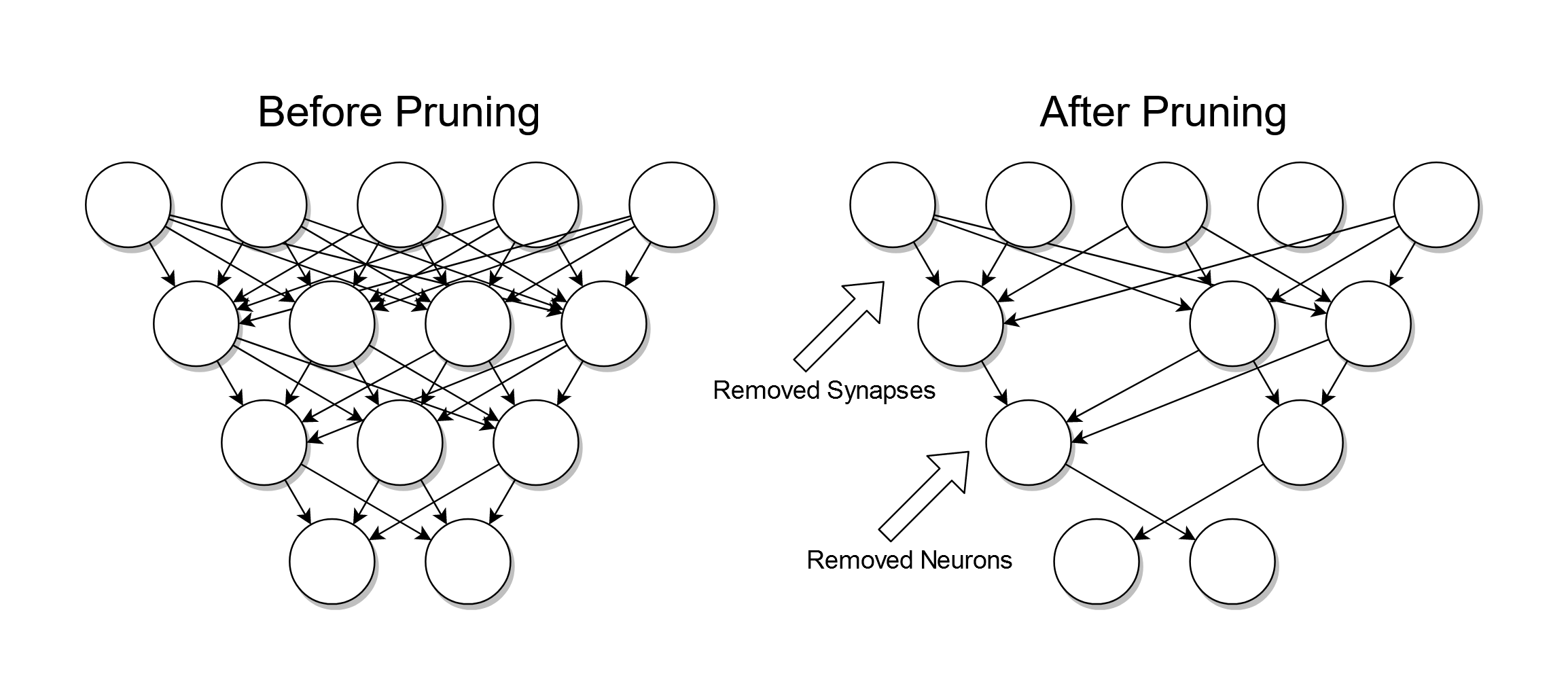
![Decision Tree Pruning](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/decision-trees%2Fdecision-tree-pruning-min.png?alt=media&token=6bfbde2d-715d-4d44-9d95-d3a4d25e5092)



### Pruning Techniques



#### Pre-Pruning

Uses stopping criteria to prevent further expansion of branches. This could be based on metrics such as Gini impurity, information gain, or a minimum number of data points.



#### Post-Pruning

Entails expanding the tree until each leaf's data points fall under a certain threshold and then **working backward** to eliminate unnecessary subtrees.



### Methods of Post-Pruning



#### Reduced-Error Pruning

This technique calculates the error on both non-leaf nodes and their corresponding leaf nodes. If pruning a node decreases the overall error, it's pruned.



#### Cost-Complexity Pruning

Also known as "weakest link pruning," this method involves assigning a 'cost' to each node based on error rates and complexity. Pruning occurs if the total cost is reduced.



#### Grafting

Instead of completely removing a subtree, grafting sees whether a simplified version of the child would have a better fit within its parent through statistical tests.



### Advantages of Tree Pruning



- **Reduction of Overfitting**: By removing noise and unwanted decisions, pruned trees are less likely to overfit to the training data.

- **Resource Efficiency**: Pruned trees are smaller in size, thereby requiring fewer computational resources for operations like classification and tree traversal.

- **Improved Interpretability**: With fewer decision nodes, the simplified tree is easier to interpret, making it easier for users and stakeholders to understand and trust model predictions.

- **Enhanced Generative Power**: Pruned trees focus more on predictive and discriminative power, contributing towards better generalization to unseen data.





## 12. How does a _Decision Tree_ avoid _overfitting_?



**Decision Trees** employ strategies to prevent overfitting by ensuring a simpler, more generalized structure. This prevents the tree from becoming too complex and tailored to the training data, while maintaining its predictive accuracy.



### Techniques to Prevent Overfitting



#### Pruning



Decision trees can be pruned, during or after construction, to remove unnecessary or redundant segments that are likely to result in overfitting.



Pruning can be conducted using:



- **Cost-Complexity Pruning:** This method involves assigning a price to each leaf node and internal node. It starts with a large tree, and as the cost decreases, the trees are pruned, allowing only those nodes to be removed that result in lower costs.

- **Minimum Cost-Complexity Pruning:** This strategy prunes the tree by limiting the growth of nodes that are likely to increase overall tree complexity.



#### Cross-Validation and Advanced Techniques



To further combat overfitting, decision trees can be optimized using more advanced methodologies such as feature selection, ensemble methods like Random Forest or Gradient Boosting, and by experimenting with improved evaluation metrics.



### Code Example: Pruning a Decision Tree



Here is the Python code:



```python

from sklearn.datasets import load_iris

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt



# Load the iris dataset and split it into training and test sets

iris = load_iris()

X, y = iris.data, iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)



# Create and fit a decision tree classifier using the Gini index for impurity measure

dt = DecisionTreeClassifier(criterion='gini', random_state=42)

dt.fit(X_train, y_train)



# Visualize the tree before pruning

plt.figure(figsize=(20,20))

plot_tree(dt, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)

plt.show()



# Use cost-complexity pruning to prune the tree

path = dt.cost_complexity_pruning_path(X_train, y_train)

ccp_alphas, impurities = path.ccp_alphas, path.impurities

dts = []

for ccp_alpha in ccp_alphas:

    dt = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alpha)

    dt.fit(X_train, y_train)

    dts.append(dt)



# Visualize the first tree after pruning

plt.figure(figsize=(20,20))

plot_tree(dts[0], filled=True, feature_names=iris.feature_names, class_names=iris.target_names)

plt.show()

```





## 13. What is the significance of the _depth_ of a _Decision Tree_?



The **depth** of a Decision Tree directly affects its predictive performance and computational efficiency.



### Key Significances



- **Model Plurality**: The tree represents uncertainty better with more branches and fewer samples in each, resulting in a clearer decision boundary.



- **Increased Accuracy**: More thorough data segregation leads to more accurate predictions. However, this improvement tapers off beyond a certain depth.



- **Computational Overheads**: Both training and inference times escalate with enhanced depth, turning the model sluggish and resource-intensive.



### Balancing Model Complexity and Efficiency



Decision Trees may exhibit **overfitting** if they grow to unmanageable depths, implying an excessive adaptation to the training dataset, at the cost of generalizability. Algorithms like ID3 and CART offer some in-built mechanisms for counteracting this tendency.



**Tree Pruning** is a post-growth technique that maximizes efficiency and generalizability of Decision Trees. It accomplishes this by removing unnecessary leaf nodes.



### Optimal Depth via Cross-Validation



Cross-Validation, a pivotal model validation approach, helps Decision Tree fitting by determining the most suitable tree depth. This method tests and gauges model performance across various tree depths and estimates the one with the best fitting.





## 14. Explain how _missing values_ are handled by _Decision Trees_.



**Decision Trees** have a **built-in mechanism** for handling missing data. This feature makes them attractive for practical use with real-world datasets, which often contain missing values.



### Handling Missing Data



In a **Decision Tree algorithm**, nodes are split based on the feature that provides the most information gain. However, they can also deal with missing data in two primary ways: they can make a decision based on the majority class, or they can distribute the sample to child nodes based on available feature values or some other global criteria.



- **Gini Impurity and Information Gain Measurement**: By using these metrics, nodes can be split in a way that minimizes impurity and maximizes information gain, even when dealing with missing data.



- **Majority Class Voting**: If a certain feature has missing values for some of the samples in a node, the algorithm can use the majority class of those samples to make a decision about that feature.



- **Distribution Across Child Nodes**: The algorithm may send samples with missing values in a particular feature to both child nodes based on, say, a probabilistic approach, where the probability of falling into each node is proportional to the impurity of that node.



### Code Example: Handling Missing Data in `scikit-learn`



Here is the Python code:



```python

from sklearn.tree import DecisionTreeClassifier

from sklearn.datasets import load_iris

import pandas as pd



# Load the dataset

data = load_iris()

X = pd.DataFrame(data.data, columns=data.feature_names)

y = data.target



# Create a Decision Tree

dtree = DecisionTreeClassifier()



# Train the model

dtree.fit(X, y)



# Make predictions

# Note: the model can handle missing data during the prediction phase as well.

# For pre-processing the data, you may use imputer from sklearn.preprocessing

# Here, we intentionally set some values in the input to NaN to simulate missing data.



X_with_missing_values = X.copy()

X_with_missing_values.iloc[::2, 1] = float('nan')



print("Input data with missing values:")

print(X_with_missing_values.head(10))



predictions = dtree.predict(X_with_missing_values)

print("Predictions:")

print(predictions)

```





## 15. Can _Decision Trees_ be used for _multi-output tasks_?



Yes, **Decision Trees** can accommodate **multi-output tasks**, and are specifically referred to as Multi-Output Trees. 



This technique is particularly useful when dealing with problems that necessitate the simultaneous prediction of multiple target variables.



### Multi-Output Trees



Multi-Output Trees enable the grouping of several dependent variables, such as:



- **Non-Correlated Responses**: When predictions across targets aren't significantly correlated.

- **Categorical and Continuous Features**: For datasets with mixed types of data.



#### Code Example: Multi-Output Regression Tree



Here is the Python code:



```python

from sklearn.datasets import make_regression

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeRegressor

import numpy as np



# Create multi-output regression data

X, y = make_regression(n_samples=100, n_features=5, n_outputs=3, random_state=42)



# Split data into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)



# Fit a multi-output Decision Tree Regressor

regr_ = DecisionTreeRegressor()

regr_.fit(X_train, y_train)



# Predict on test set

y_pred = regr_.predict(X_test)



# Check R-squared score

r2_score = regr_.score(X_test, y_test)

print("R-squared score: {:.2f}".format(r2_score))

```





#### Explore all 60 answers here 👉 [Devinterview.io - Decision Tree](https://devinterview.io/questions/machine-learning-and-data-science/decision-tree-interview-questions)









machine-learning-and-data-science