Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/devinterview-io/hash-table-data-structure-interview-questions

🟣 Hash Table Data Structure interview questions and answers to help you prepare for your next data structures and algorithms interview in 2024.
https://github.com/devinterview-io/hash-table-data-structure-interview-questions

algorithms algorithms-and-data-structures algorithms-and-data-structures-interview-questions algorithms-interview-questions coding-interview-questions data-structures data-structures-and-algorithms data-structures-and-algorithms-interview-questions data-structures-interview-questions hash-table-data-structure hash-table-data-structure-interview-questions hash-table-data-structure-questions hash-table-data-structure-tech-interview software-architecture-interview software-architecture-interview-questions software-developer-interview software-engineer-interview

Last synced: about 1 month ago
JSON representation

🟣 Hash Table Data Structure interview questions and answers to help you prepare for your next data structures and algorithms interview in 2024.

Awesome Lists containing this project

README 

        
# 39 Must-Know Hash Table Data Structure Interview Questions









data-structures-and-algorithms






#### You can also find all 39 answers here 👉 [Devinterview.io - Hash Table Data Structure](https://devinterview.io/questions/data-structures-and-algorithms/hash-table-data-structure-interview-questions)







## 1. What is a _Hash Table_?



A **Hash Table**, also known as a **Hash Map**, is a data structure that provides a mechanism to **store** and **retrieve data** based on **key-value** pairs.



It is an **associative array** abstract data type where the key is hashed, and the resulting hash value is used as an index to locate the corresponding value in a **bucket** or **slot**.



### Key Features



- **Unique Keys**: Each key in the hash table maps to a single value.

- **Dynamic Sizing**: Can adjust its size based on the number of elements.

- **Fast Operations**: Average time complexity for most operations is $O(1)$.



### Visual Representation



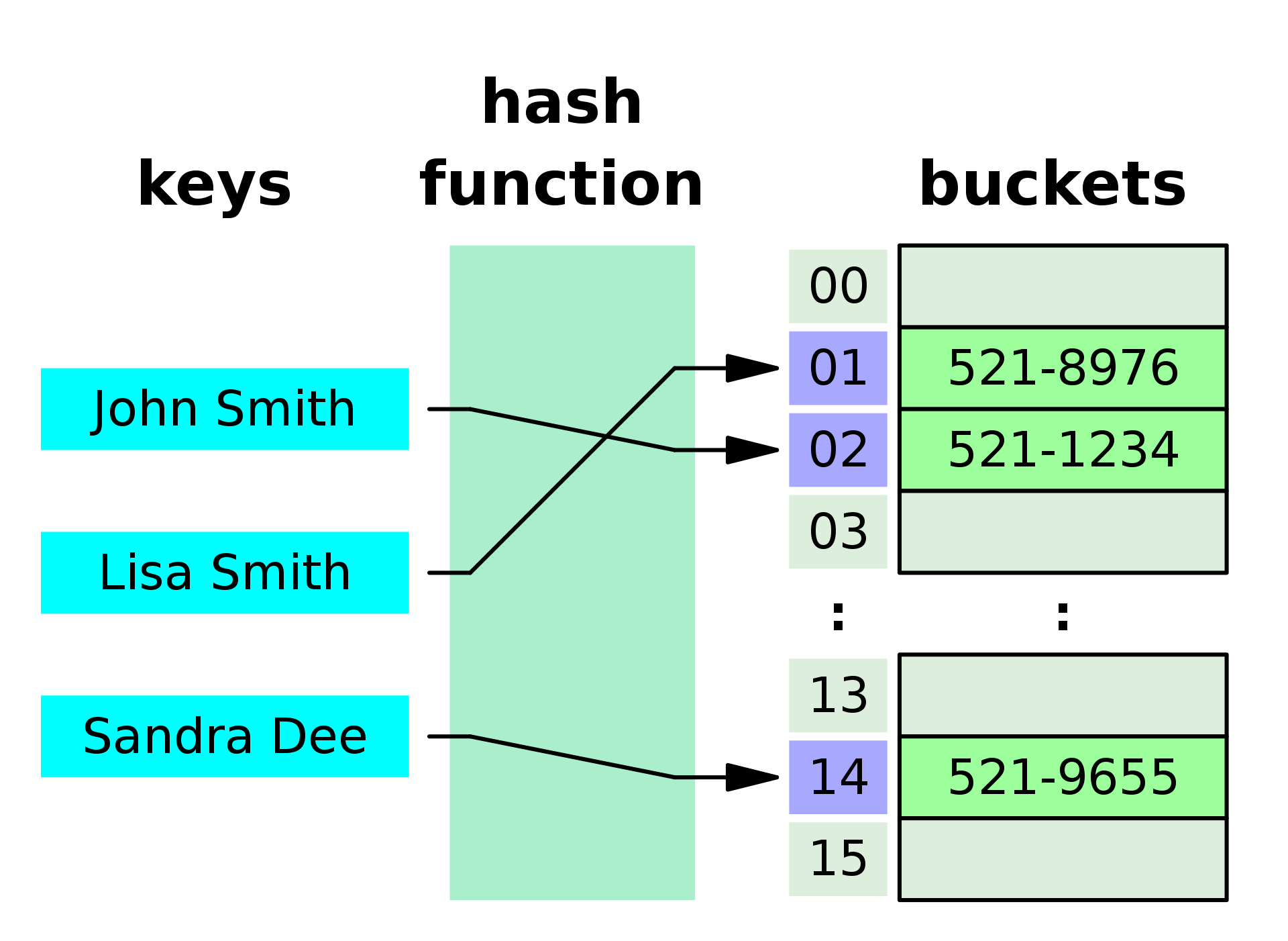
![Hash Table Example](https://upload.wikimedia.org/wikipedia/commons/thumb/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg/1920px-Hash_table_3_1_1_0_1_0_0_SP.svg.png)



### Core Components



#### Hash Function



The **hash function** converts each key to a numerical **hash value**, which is then used to determine the storage location, or "bucket."



#### Buckets



**Buckets** are containers within the hash table that hold the key-value pairs. The hash function aims to distribute keys uniformly across buckets to minimize collisions.



### Collision Handling



- **Open-Addressing**: Finds the next available bucket if a collision occurs.

- **Chaining**: Stores colliding keys in a linked list within the same bucket.



### Complexity Analysis



- **Time Complexity**: $O(1)$ - average and best-case, $O(n)$ - worst-case.

- **Space Complexity**: $O(n)$



### Code Example: Hash Table



Here is the Python code:



```python

# Initialize a hash table

hash_table = {}



# Add key-value pairs

hash_table['apple'] = 5

hash_table['banana'] = 2

hash_table['cherry'] = 3



# Retrieve a value

print(hash_table['apple'])  # Output: 5



# Update a value

hash_table['banana'] = 4



# Remove a key-value pair

del hash_table['cherry']

```





## 2. What is _Hashing_?



**Hashing** is a method that maps data to fixed-size values, known as **hash values**, for efficient storage and retrieval. A **hash function** generates these values, serving as the data's unique identifier or key.



### Key Features



- **Speed**: Hashing offers constant-time complexity for data operations.

- **Data Integrity**: A good hash function ensures even minor data changes will yield different hash values.

- **Security**: Cryptographic hashes are essential in secure data transmission.

- **Collision Management**: While hash collisions can occur, they are manageable and typically rare.



### Hash Functions and Hash Values



A **hash function** generates a fixed-size **hash value**, serving as the data's unique identifier or key for various applications like data indexing and integrity checks. Hash values are typically represented as **hexadecimal numbers**.



#### Key Characteristics



- **Deterministic**: The same input will always produce the same hash value.

- **Fixed-Length Output**: Outputs have a consistent length, making them suitable for data structures like hash tables.

- **Speed**: Hash functions are designed for quick computation.

- **One-Way Functionality**: Reconstructing the original input from the hash value should be computationally infeasible.

- **Avalanche Effect**: Small input changes should result in significantly different hash values.

- **Collision Resistance**: While it's difficult to completely avoid duplicate hash values for unique inputs, well-designed hash functions aim to minimize this risk.



### Popular Hashing Algorithms



- **MD5**: Obsolete due to vulnerabilities.

- **SHA Family**:

  - SHA-1: Deprecated; collision risks.

  - SHA-256: Widely used in cryptography.



### Practical Applications



- **Databases**: For quick data retrieval through hash indices.

- **Distributed Systems**: For data partitioning and load balancing.

- **Cryptography**: To ensure data integrity.

- **Caching**: For efficient in-memory data storage and access.



### Code Example: SHA-256 with `hashlib`



Here is the Python code:



```python

import hashlib



def compute_sha256(s):

    hasher = hashlib.sha256(s.encode())

    return hasher.hexdigest()



print(compute_sha256("Hello, World!"))

```





## 3. Explain the difference between _Hashing_ and _Hash Tables_.



When discussing **Hashing** and **Hash Tables**, it's crucial to recognize that one is a **technique** while the other is a **data structure**. Here's a side-by-side comparison:



### Key Distinctions



#### Definition



- **Hashing**: A computational technique that converts input (often a string) into a fixed-size value, referred to as a hash value.

- **Hash Tables**: A data structure that utilizes hash values as keys to efficiently store and retrieve data in memory.



#### Primary Function



- **Hashing**: To generate a unique identifier (hash value) for a given input, ensuring consistency and rapid computation.

- **Hash Tables**: To facilitate quick access to data by mapping it to a hash value, which determines its position in the table.



#### Application Areas



- **Hashing**: Common in cryptography for secure data transmission, data integrity checks, and digital signatures.

- **Hash Tables**: Used in programming and database systems to optimize data retrieval operations.



#### Inherent Complexity



- **Hashing**: Focuses solely on deriving a hash value from input data.

- **Hash Tables**: Incorporates mechanisms to manage issues like hash collisions (when two distinct inputs produce the same hash value) and may also involve dynamic resizing to accommodate growing datasets.



#### Operational Performance



- **Hashing**: Producing a hash value is typically an $O(1)$ operation, given a consistent input size.

- **Hash Tables**: On average, operations such as data insertion, retrieval, and deletion have $O(1)$ time complexity, although worst-case scenarios can degrade performance.



#### Persistence



- **Hashing**: Transient in nature; once the hash value is generated, the original input data isn't inherently stored or preserved.

- **Hash Tables**: Persistent storage structure; retains both the input data and its corresponding hash value in the table.





## 4. Provide a simple example of a _Hash Function_.



The **parity function** can serve as a rudimentary example of a **hash function**. It takes a single input, usually an integer, and returns either `0` or `1` based on whether the input number is even or odd.



### Properties of the Parity Function



- **Deterministic**: Given the same number, the function will always return the same output.

- **Efficient**: Computing the parity of a number can be done in constant time.

- **Small Output Space**: The output is limited to two possible values, `0` or `1`.

- **One-Way Function**: Given one of the outputs (`0` or `1`), it is impossible to determine the original input.



### Code Example: Parity Function



Here is the Python code:



```python

def hash_parity(n: int) -> int:

    if n % 2 == 0:

        return 0

    return 1

```



### Real-World Hash Functions



While the parity function serves as a simple example, **real-world hash functions** are much more complex. They often use cryptographic algorithms to provide a higher level of security and other features like the ones mentioned below:



- **Cryptographic Hash Functions**: Designed to be secure against various attacks like pre-image, second-pre-image, and collision.

- **Non-Cryptographic Hash Functions**: Used for general-purpose applications, data storage, and retrieval.

- **Perfect Hash Functions**: Provide a unique hash value for each distinct input.





## 5. How do hash tables work under the hood, specifically in languages like Java, Python, and C++?



**Hash tables** are at the core of many languages, such as Java, Python, and C++:



### Core Concepts



- **Key Insights**: Hash tables allow for fast data lookups based on key values. They use a technique called hashing to map keys to specific memory locations, enabling $O(1)$ time complexity for key-based operations like insertion, deletion, and search.



- **Key Mapping**: This is often implemented through a hash function, a mathematical algorithm that **converts keys into unique integers** (hash values or hash codes) within a fixed range. The hash value then serves as an index to directly access the memory location where the key's associated value is stored.



- **Handling Collisions**:

   - **Challenges**: Two different keys can potentially hash to the same index, causing what's known as a **collision**.

   - **Solutions**:

     - **Separate Chaining**: Affected keys and their values are stored in separate data structures, like linked lists or trees, associated with the index. The hash table then maps distinct hash values to each separate structure.

     - **Open Addressing**: When a collision occurs, the table is probed to find an alternative location (or address) for the key using specific methods.



### Collision Handling in Python, Java, and C++



- **Python**

  - **Data Structure**: Python uses an array of pointers to **linked lists**. Each linked list is called a "bucket" and contains keys that hash to the same index.

    ```python

    hashtab[hash(key) % size].insert(key, val)

    ```

  - **Size Dynamics**: Python uses dynamic resizing, and its load factor dictates when resizing occurs.



- **Java**

  - **Data Structure**: The `HashMap` class uses an array of **TreeNodes** and **LinkedLists**, converting to trees after a certain threshold.

  - **Size Dynamics**: Java also resizes dynamically, triggered when the number of elements exceeds a load factor.



- **C++ (Standard Library)**

  - **Data Structure**: Starting from C++11, the standard library `unordered_map` typically implements hash tables as resizable arrays of **linked lists**.

  - **Size Dynamics**: It also resizes dynamically when the number of elements surpasses a certain load factor.



Do note that C++ has several that may get used in hash tables, and it also uses separate chaining as a collision avoidance technique.



### The Complexity Behind Lookups



While hash tables provide **constant-time lookups** in the average case, several factors can influence their performance:



- **Hash Function Quality**: A good hash function distributes keys more evenly, promoting better performance. Collisions, especially frequent or hard-to-resolve ones, can lead to performance drops.

- **Load Factor**: This is the ratio of elements to buckets. When it gets too high, the structure becomes less efficient, and resizing can be costly. Java and Python automatically manage load factors during resizing.

- **Resizing Overhead**: Periodic resizing (to manage the load factor) can pause lookups, leading to a one-time performance hit.





## 6. What are _Hash Collisions_?



In hash functions and tables, a **hash collision** occurs when two distinct keys generate the same hash value or index. Efficiently addressing these collisions is crucial for maintaining the hash table's performance.



### Causes of Collisions



- **Hash Function Limitations**: No hash function is perfect; certain datasets may result in more collisions.

- **Limited Hash Space**: Due to the Pigeonhole Principle, if there are more unique keys than slots, collisions are inevitable.



### Collisions Types



- **Direct**: When two keys naturally map to the same index.

- **Secondary**: Arising during the resolution of a direct collision, often due to strategies like chaining or open addressing.



### Probability



The likelihood of a collision is influenced by the hash function's design, the number of available buckets, and the table's load factor.



**Worst-case** scenarios where all keys collide to the same index, can degrade a hash table's performance from $O(1)$ to $O(n)$.



### Strategies for Collision Resolution



- **Chaining**: Each slot in the hash table contains a secondary data structure, like a linked list, to hold colliding keys.

- **Open Addressing**: The hash table looks for the next available slot to accommodate the colliding key.

- **Cryptographic Hash Functions**: These are primarily used to ensure data integrity and security due to their reduced collision probabilities. However, they're not commonly used for general hash tables because of their slower performance.



### Illustrative Example



Consider a hash table that employs chaining to resolve collisions:



| Index | Keys        |

|-------|-------------|

| 3     | key1, key2  |



Inserting a new key that hashes to index 3 causes a collision. With chaining, the new state becomes:



| Index | Keys           |

|-------|----------------|

| 3     | key1, key2, key7 |



### Key Takeaways



- **Hash Collisions are Inevitable**: Due to inherent mathematical and practical constraints.

- **Strategies Matter**: The efficiency of a hash table can be significantly influenced by the chosen collision resolution strategy.

- **Probability Awareness**: Being aware of collision probabilities is vital, especially in applications demanding high performance or security.





## 7. Name some _Collision Handling Techniques_.



In **hash tables**, **collisions** occur when different keys yield the same index after being processed by the hash function. Let's look at common collision-handling techniques:



### Chaining



**How it Works**: Each slot in the table becomes the head of a linked list. When a collision occurs, the new key-value pair is appended to the list of that slot.



**Pros**: 

- Simple to implement.

- Handles high numbers of collisions gracefully.



**Cons**: 

- Requires additional memory for storing list pointers.

- Cache performance might not be optimal due to linked list traversal.



### Linear Probing



**How it Works**: If a collision occurs, the table is probed linearly (i.e., one slot at a time) until an empty slot is found.



**Pros**: 

- Cache-friendly as elements are stored contiguously.



**Cons**: 

- Clustering can occur, slowing down operations as the table fills up.

- Deleting entries requires careful handling to avoid creating "holes."



### Double Hashing



**How it Works**: Uses two hash functions. If the first one results in a collision, the second hash function determines the step size for probing.



**Pros**: 

- Reduces clustering compared to linear probing.

- Accommodates a high load factor.



**Cons**: 

- More complex to implement.

- Requires two good hash functions.



### Code Example: Chaining



Here is the Python code:



```python

class Node:

    def __init__(self, key, value):

        self.key = key

        self.value = value

        self.next = None



class HashTableWithChaining:

    def __init__(self, size):

        self.table = [None] * size



    def _hash(self, key):

        return hash(key) % len(self.table)



    def insert(self, key, value):

        index = self._hash(key)

        new_node = Node(key, value)

        

        # If slot is empty, simply assign it to the new node

        if self.table[index] is None:

            self.table[index] = new_node

            return



        # If slot is occupied, traverse to the end of the chain and append

        current = self.table[index]

        while current:

            if current.key == key:

                current.value = value  # Overwrite if key already exists

                return

            if not current.next:

                current.next = new_node  # Append to the end

                return

            current = current.next



    def get(self, key):

        index = self._hash(key)

        current = self.table[index]

        while current:

            if current.key == key:

                return current.value

            current = current.next

        return None



# Example Usage:



hash_table = HashTableWithChaining(10)

hash_table.insert("key1", "value1")

hash_table.insert("key2", "value2")

hash_table.insert("key3", "value3")

hash_table.insert("key1", "updated_value1")  # Update existing key



print(hash_table.get("key1"))  # Output: updated_value1

print(hash_table.get("key2"))  # Output: value2

```



### Code Example: Linear Probing



Here is the Python code:



```python

class HashTable:

    def __init__(self, size):

        self.table = [None] * size



    def _hash(self, key):

        return hash(key) % len(self.table)



    def insert(self, key, value):

        index = self._hash(key)

        while self.table[index] is not None:

            if self.table[index][0] == key:

                break

            index = (index + 1) % len(self.table)

        self.table[index] = (key, value)



    def get(self, key):

        index = self._hash(key)

        while self.table[index] is not None:

            if self.table[index][0] == key:

                return self.table[index][1]

            index = (index + 1) % len(self.table)

        return None

```



### Code Example: Double Hashing



Here is the Python code:



```python

class DoubleHashingHashTable:

    def __init__(self, size):

        self.table = [None] * size



    def _hash1(self, key):

        return hash(key) % len(self.table)



    def _hash2(self, key):

        return (2 * hash(key) + 1) % len(self.table)



    def insert(self, key, value):

        index = self._hash1(key)

        step = self._hash2(key)

        while self.table[index] is not None:

            if self.table[index][0] == key:

                break

            index = (index + step) % len(self.table)

        self.table[index] = (key, value)



    def get(self, key):

        index = self._hash1(key)

        step = self._hash2(key)

        while self.table[index] is not None:

            if self.table[index][0] == key:

                return self.table[index][1]

            index = (index + step) % len(self.table)

        return None

```





## 8. Describe the characteristics of a good hash function.



A **good hash function** is fundamental for efficient data management in **hash tables** or when employing techniques such as **hash-based encryption**. Here, let's go through what it means for a hash function to be **high-quality**.



### Key Features



- **Deterministic**: The function should consistently map the same input to the same hash value.

- **Fast Performance**: Ideally, the function should execute in $O(1)$ time for typical use.



### Minimizing Collisions



Collision is the term when two different keys have the same hash value.



- **Few collisions**: A good hash function minimizes the number of collisions when it is possible.

- **Uniformly Distributed Hash Values**: Each output hash value or, in the context of a hash table, each storage location should be equally likely for the positive performance of the hash table.



### Desirable Behavioral Qualities



- **Security Considerations**: In the context of cryptographic hash functions, the one-way nature is essential, meaning it is computationally infeasible to invert the hash value.

- **Value Independence**: Small changes in the input should result in substantially different hash values, also known as the avalanche effect.



### Code Example: Basic Hash Function



Here is the Python code:



```python

def basic_hash(input_string):

    '''A simple hash function using ASCII values'''

    hash_val = 0

    for char in input_string:

        hash_val += ord(char)

    return hash_val

```



This hash function sums up the ASCII values of the characters in `input_string` to get its hash value. While this function is easy to implement and understand, it is **not a good choice in practice** as it may not meet the characteristics mentioned above.



### Code Example: Secure Hash Function



Here is the Python code:



```python

import hashlib



def secure_hash(input_string):

    '''A secure hash function using SHA-256 algorithm'''

    hash_object = hashlib.sha256(input_string.encode())

    hash_hex = hash_object.hexdigest()

    return hash_hex

```



In this example, the `hashlib` library allows us to implement a cryptographic hash function using the SHA-256 algorithm. This algorithm is characterized by high security and the one-way nature essential for securing sensitive data.





## 9. What is _Separate Chaining_, and how does it handle collisions?



**Separate Chaining** is a collision resolution technique employed in **Hash Tables**. This method entails maintaining a list of entries, often implemented as a linked list, for each bucket.



### Key Benefits



- **Effective Collision Handling**: It provides a consistent utility irrespective of the number of keys hashed.

- **Easy to Implement and Understand**: This technique is relatively simple and intuitive to implement.



### Procedure Overview



1. **Bucket Assignment**: Each key hashes to a specific "bucket," which could be a position in an array or a dedicated location in memory.

2. **Internal List Management**: Keys within the same bucket are stored sequentially. Upon a collision, keys are appended to the appropriate bucket.



**Search Performances**



- Best-Case $O(1)$: The target key is the only entry in its bucket.

- Worst-Case $O(n)$: All keys in the table hash to the same bucket, and a linear search through the list is necessary.



### Code Example: Separate Chaining



Here is the Python code:



```python

# Node for key-value storage in the linked list

class Node:

    def __init__(self, key, value):

        self.key = key

        self.value = value

        self.next = None



# Hash table using separate chaining

class HashTable:

    def __init__(self, capacity):

        self.capacity = capacity

        self.buckets = [None] * capacity  # Initialize buckets with None



    def hash(self, key):

        return hash(key) % self.capacity  # Basic hash function using modulo



    def insert(self, key, value):

        index = self.hash(key)

        node = Node(key, value)

        if self.buckets[index] is None:

            self.buckets[index] = node

        else:

            # Append to the end of the linked list

            current = self.buckets[index]

            while current:

                if current.key == key:

                    current.value = value  # Update the value for existing key

                    return

                if current.next is None:

                    current.next = node

                    return

                current = current.next



    def search(self, key):

        index = self.hash(key)

        current = self.buckets[index]

        while current:

            if current.key == key:

                return current.value

            current = current.next

        return None

```





## 10. Explain _Open Addressing_ and its different probing techniques.



**Open Addressing** is a collision resolution technique where a hash table dynamically looks for alternative slots to place a colliding element.



### Probing Techniques



1. **Linear Probing**: When a collision occurs, investigate cells in a consistent sequence. The operation is mathematically represented as:



$$

(h(k) + i) \mod m, \quad  \text{for} \ i = 0, 1, 2, \ldots

$$



Here, $h(k)$ is the key's hash value, $m$ is the table size, and $i$ iterates within the modulo operation.



2. **Quadratic Probing**: The cells to search are determined by a quadratic function:



$$

(h(k) + c_1i + c_2i^2) \mod m

$$



Positive constants $c1$ and $c2$ are used as increment factors. If the table size is a prime number, these constants can equal 1 and 1, respectively. This scheme can still result in clustering.



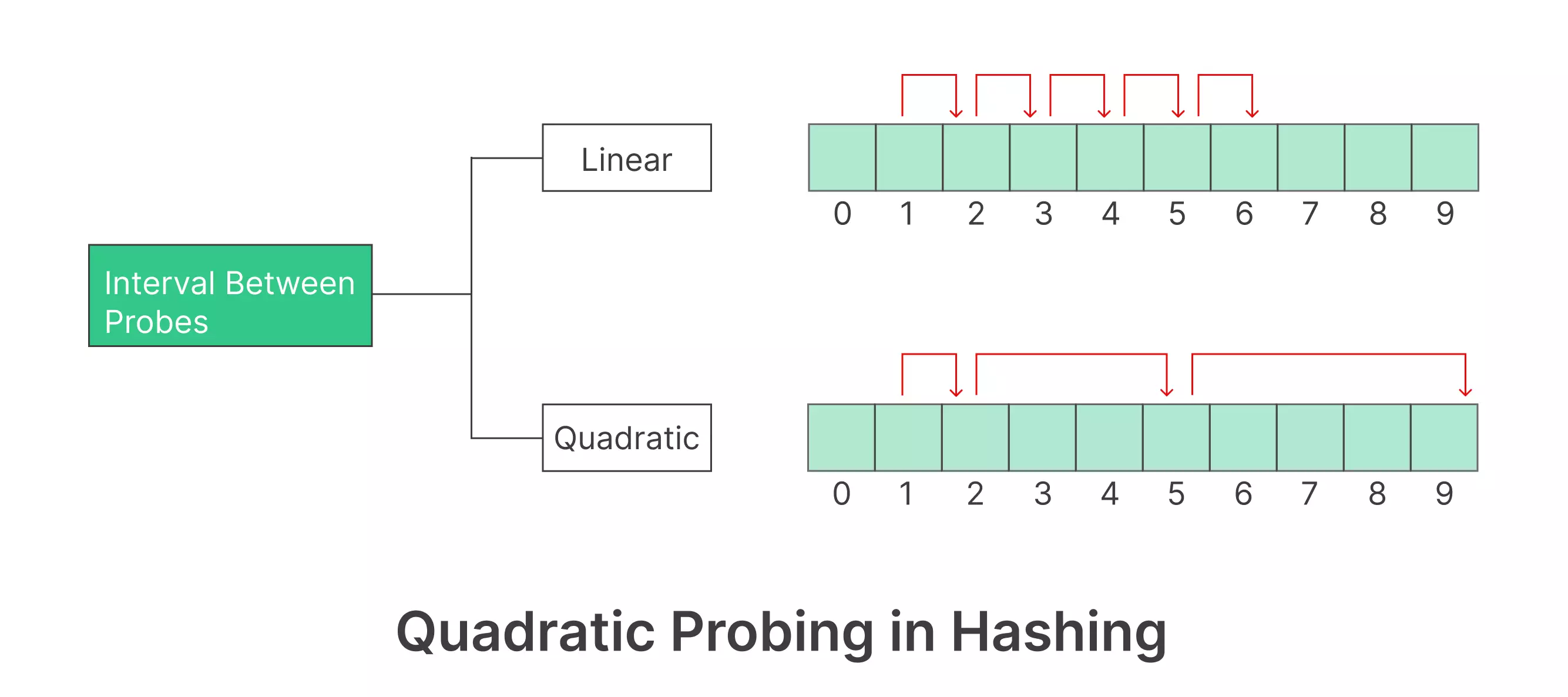
![Linear and Quadratic probing in hashing](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/hash-tables%2Flinear-and-quadratic-probing-in-hashing.webp?alt=media&token=2aca1d94-be59-4c05-aa4d-2b3d50899053)



4. **Double Hashing**: Unlike with linear or quadratic probing, the second hash function $h_2(k)$ computes the stride of the probe. The operation is:



$$

(h(k) + ih_2(k)) \mod m

$$



**Note**: It's crucial for the new probe sequence to cover all positions in the table, thereby ensuring that every slot has the same probability of being the data's final location.





## 11. Explain the _Time_ and _Space Complexity_ of a _Hash Table_.



**Hash tables** offer impressive time and space performance under most conditions. Here's a detailed breakdown:



### Time Complexity



- **Best Case $O(1)$**: With uniform distribution and no collisions, fundamental operations like lookup, insertion, and deletion are constant-time.



- **Average and Amortized Case $O(1)$**: Even with occasional collisions and rehashing, most operations typically remain constant-time. While rehashing can sometimes take $O(n)$, its infrequency across many $O(1)$ operations ensures an overall constant-time complexity.



- **Worst Case $O(n)$**: Arises when all keys map to one bucket, forming a linked list. Such cases are rare and typically result from suboptimal hash functions or unique data distributions.



### Space Complexity $O(n)$



The primary storage revolves around the $n$ elements in the table. Additional overhead from the structure itself is minimal, ensuring an upper bound of $O(n)$. The "load factor," indicating the ratio of stored elements to the table's capacity, can impact memory use.





## 12. What is a _Load Factor_ in the context of _Hash Tables_?



The **load factor** is a key performance metric for hash tables, serving as a threshold for resizing the table. It balances time and space complexity by determining when the table is full enough to warrant expansion.



### Formula and Calculation



The load factor is calculated using the following formula:



$$

\text{{Load Factor}} = \frac{{\text{{Number of elements}}}}{{\text{{Number of buckets}}}}

$$



It represents the ratio of stored elements to available buckets.



### Key Roles and Implications



1. **Space Efficiency**: It helps to minimize the table's size, reducing memory usage.

2. **Time Efficiency**: A well-managed load factor ensures constant-time operations for insertion and retrieval.

3. **Collision Management**: A high load factor can result in more collisions, affecting performance.

4. **Resizing**: The load factor is a trigger for resizing the table, which helps in redistributing elements.



### Best Practices



- **Standard Defaults**: Libraries like Java's `HashMap` or Python's `dict` usually have well-chosen default load factors.

- **Balanced Values**: For most use-cases, a load factor between 0.5 and 0.75 strikes a good balance between time and space.

- **Dynamic Adjustments**: Some advanced hash tables, such as Cuckoo Hashing, may adapt the load factor for performance tuning.



### Load Factor vs. Initial Capacity



The initial capacity is the starting number of buckets, usually a power of 2, while the load factor is a relative measure that triggers resizing. They serve different purposes in the operation and efficiency of hash tables.





## 13. How does the load factor affect performance in a hash table?



The **load factor** is a key parameter that influences the performance and memory efficiency of a hashtable. It's a measure of how full the hashtable is and is calculated as:



$$

\text{Load Factor} = \frac{\text{Number of Entries}}{\text{Number of Buckets}}

$$



### Core Mechanism



When the load factor exceeds a certain predetermined threshold, known as the **rehashing or resizing threshold**, the table undergoes a resizing operation. This triggers the following:



- **Rehashing**: Every key-value pair is reassigned to a new bucket, often using a new hash function.

- **Reallocating memory**: The internal data structure grows or shrinks to ensure a better balance between load factor and performance.



### Performance Considerations



- **Insertions**: As the load factor increases, the number of insertions before rehashing decreases. Consequently, insertions can be faster with a smaller load factor, albeit with a compromise on memory efficiency.

- **Retrievals**: In a well-maintained hash table, retrievals are expected to be faster with a smaller load factor.



However, these ideal situations might not hold in practice due to these factors:



- **Cache Efficiency**: A smaller load factor might result in better cache performance, ultimately leading to improved lookup speeds.



- **Access Patterns**: If insertions and deletions are frequent, a higher load factor might be preferable to avoid frequent rehashing, which can lead to performance overhead.



### Code Example: Load Factor and Rehashing



Here is the Python code:



```python

class HashTable:

    def __init__(self, initial_size=16, load_factor_threshold=0.75):

        self.initial_size = initial_size

        self.load_factor_threshold = load_factor_threshold

        self.buckets = [None] * initial_size

        self.num_entries = 0



    def insert(self, key, value):

        # Code for insertion

        self.num_entries += 1

        current_load_factor = self.num_entries / self.initial_size

        if current_load_factor > self.load_factor_threshold:

            self.rehash()



    def rehash(self):

        new_size = self.initial_size * 2  # Doubling the size

        new_buckets = [None] * new_size

        # Code for rehashing

        self.buckets = new_buckets

```





## 14. Discuss different ways to _resize a hash table_. What is the complexity involved?



Resizing a hash table is essential to **maintain efficiency** as the number of elements in the table grows. Let's look at different strategies for resizing and understand their time complexities.



### Collision Resolution Strategy Affects Resizing Complexity



Resizing a hash table with **separate chaining** and **open addressing** entails different methods and time complexities:



- **Separate Chaining**: Direct and has a time complexity of $O(1)$ for individual insertions.

- **Open Addressing**: Requires searching for a new insertion position, which can make the insertion $O(n)$ in the worst-case scenario. For handling existing elements during resizing, the complexity is $O(n)$. Common heuristics and strategies, such as **Lazy Deletion** or **Double Hashing**, can help mitigate this complexity.



### Array Doubling and Halving



**Array resizing** is the most common method due to its simplicity and efficiency. It achieves dynamic sizing by doubling the array size when it becomes too crowded and halving when occupancy falls below a certain threshold.



- **Doubling Size**: This action, also known as **rehashing**, takes $O(n)$ time, where $n$ is the current number of elements. For each item currently in the table, the hash and placement in the new, larger table require $O(1)$ time.

- **Halving Size**: The table needs rescaling when occupancy falls below a set threshold. The current table is traversed, and all elements are hashed for placement in a newly allocated, smaller table, taking $O(n)$ time.



### List of Add/Drop in Dynamic Table Resizing



- Resizing a dynamic list denoted as a table:



| Operation               | Time Complexity |

|------------------------|-----------------|

| Insert/Drop at the end  |   O(1)          |

| Insert/Drop at any position| O(1)          |

| Doubling/Halving        |   O(n)          |



### Code: Array Doubling & Halving



Here is the Python code:



```python

class HashTable:

    def __init__(self, size):

        self.size = size

        self.threshold = 0.7  # Example threshold

        self.array = [None] * size

        self.num_elements = 0



    def is_overloaded(self):

        return self.num_elements / self.size > self.threshold



    def is_underloaded(self):

        return self.num_elements / self.size < 1 - self.threshold



    def resize(self, new_size):

        old_array = self.array

        self.array = [None] * new_size

        self.size = new_size

        self.num_elements = 0



        for item in old_array:

            if item is not None:

                self.insert(item)



    def insert(self, key):

        if self.is_overloaded():

            self.resize(self.size * 2)

        

        # Insert logic

        self.num_elements += 1



    def delete(self, key):

        # Deletion logic

        self.num_elements -= 1



        if self.is_underloaded():

            self.resize(self.size // 2)

```





## 15. How can the choice of a hash function impact the efficiency of a hash table?



The efficiency of a **hash table** relies significantly on the hash function used. An inadequate hash function can lead to **clustering**, where multiple keys map to the same bucket, degrading **performance** to **O(n)**, essentially turning the hash table into an unordered list.



On the other hand, a good hash function achieves a uniform distribution of keys, maximizing the **O(1) operations**. Achieving balance requires careful selection of the **hash function** and understanding its impact on **performance**.



### Metrics for Hash Functions



- **Uniformity**: Allowing for an even distribution of keys across buckets.

  

- **Consistency**: Ensuring repeated calls with the same key return the same hash.

  

- **Minimizing Collisions**: A good function minimizes the chances of two keys producing the same hash.



### Examples of Commonly Used Hash Functions



- **Identity Function**: While simple, it doesn't support uniform distribution. It is most useful for testing or as a placeholder while the system is in development.

  

- **Modulous Function**: Useful for small tables and keys that already have a uniform distribution. Be cautious with such an implementation, especially with table resizing.

  

- **Division Method**: This hash function employs division to spread keys across defined buckets. The efficiency of this method can depend on the prime number that is used as the divisor.



- **MurmurHash**: A non-cryptographic immersion algorithm, known for its speed and high level of randomness, making it suitable for general-purpose hashing.

  

- **MD5 and SHA Algorithms**: While designed for cryptographic use, they still can be used in hashing where security is not a primary concern. However, they are slower than non-cryptographic functions for hashing purposes.



### General Tips for Hash Function Selection



- **Keep it Simple**: Hash functions don't have to be overly complex. Sometimes, a straightforward approach suffices.



- **Understand the Data**: The nature of the data being hashed can often point to the most appropriate type of function.



- **Protect Against Malicious Data**: If your data source isn't entirely trustworthy, consider a more resilient hash function.





#### Explore all 39 answers here 👉 [Devinterview.io - Hash Table Data Structure](https://devinterview.io/questions/data-structures-and-algorithms/hash-table-data-structure-interview-questions)









data-structures-and-algorithms