Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/devinterview-io/recursion-algorithm-interview-questions

🟣 Recursion Algorithm interview questions and answers to help you prepare for your next data structures and algorithms interview in 2024.
https://github.com/devinterview-io/recursion-algorithm-interview-questions

algorithms algorithms-and-data-structures algorithms-and-data-structures-interview-questions algorithms-interview-questions coding-interview-questions data-structures data-structures-and-algorithms data-structures-and-algorithms-interview-questions data-structures-interview-questions recursion-algorithm recursion-algorithm-interview-questions recursion-algorithm-questions recursion-algorithm-tech-interview software-architecture-interview software-architecture-interview-questions software-developer-interview software-engineer-interview

Last synced: about 23 hours ago
JSON representation

🟣 Recursion Algorithm interview questions and answers to help you prepare for your next data structures and algorithms interview in 2024.

Awesome Lists containing this project

README 

        
# 53 Core Recursion Algorithm Interview Questions









data-structures-and-algorithms






#### You can also find all 53 answers here 👉 [Devinterview.io - Recursion Algorithm](https://devinterview.io/questions/data-structures-and-algorithms/recursion-algorithm-interview-questions)







## 1. How _Dynamic Programming_ is different from _Recursion_ and _Memoization_?



**Dynamic Programming** (DP), **Recursion**, and **Memoization** are techniques for solving problems that can be divided into smaller, overlapping sub-problems. While they share this commonality, they each offer unique advantages and limitations. 



### Key Distinctions



1. **Efficiency**: DP typically leads to polynomial-time algorithms, whereas Recursion and Memoization can result in higher time complexities.

  

2. **Problem-Solving Direction**: DP builds solutions from the ground up, focusing on smaller sub-problems first. In contrast, Recursion and Memoization usually adopt a top-down approach.



3. **Implementation Style**: DP and Memoization can be implemented either iteratively or recursively, while Recursion is, by definition, a recursive technique.



4. **Sub-Problem Coverage**: DP aims to solve all relevant sub-problems, whereas Memoization and Recursion solve sub-problems on an as-needed basis.



5. **Memory Use**: DP often requires less memory than Memoization, as it doesn't store every state reached through recursive calls.





## 2. What are some _Common Examples of Recursion_ in computer science?



Let's look into some examples and see how they utilize the core concepts of **recursion**.



### 1. Binary Tree Traversal



In binary tree traversal, nodes are visited **recursively**, exploring the left and right subtrees in various orders.



```python

class Node:

    def __init__(self, value):

        self.value = value

        self.left = None

        self.right = None



def in_order_traversal(node):

    if node is not None:

        in_order_traversal(node.left)

        print(node.value)

        in_order_traversal(node.right)

```



### 2. Palindrome Check



A **palindrome** is a word, phrase, number, or other sequence of characters that reads the same forward and backward. To determine a palindrome, the outer characters of a word are compared. If they match, the inner substring is checked recursively.



```python

def is_palindrome(word):

    if len(word) <= 1:

        return True

    if word[0] == word[-1]:

        return is_palindrome(word[1:-1])

    return False

```



### 3. Factorial Calculation



The factorial of a number is calculated using a **base** and **recursive** case. $0! = 1$ and $n! = n \times (n-1)!$.



```python

def factorial(n):

    if n == 0:

        return 1

    return n * factorial(n-1)

```



### 4. Folder Hierarchy



A folder hierarchy in a file system can be traversed recursively, exploring the contents of each directory.



```python

import os



def folder_contents(path):

    for item in os.listdir(path):

        item_path = os.path.join(path, item)

        if os.path.isfile(item_path):

            print(f"Found a file: {item_path}")

        elif os.path.isdir(item_path):

            print(f"Entering folder: {item_path}")

            folder_contents(item_path)

```



### 5. Towers of Hanoi



The Towers of Hanoi is a mathematical puzzle that involves three pegs and a set of disks of different sizes, which can be moved from one peg to another following a set of rules. It's often used as an example in computer science textbooks to illustrate how recursion can be used to solve problems.



```python

def tower_of_hanoi(n, source, target, auxiliary):

    if n == 1:

        print(f"Move disk 1 from {source} to {target}")

        return

    tower_of_hanoi(n-1, source, auxiliary, target)

    print(f"Move disk {n} from {source} to {target}")

    tower_of_hanoi(n-1, auxiliary, target, source)

```



### 6. Merge Sort



This sorting algorithm follows the **divide-and-conquer** paradigm, using recursion to split and then merge lists.



```python

def merge_sort(arr):

    if len(arr) <= 1:

        return arr

    mid = len(arr) // 2

    left_half = arr[:mid]

    right_half = arr[mid:]

    left_half = merge_sort(left_half)

    right_half = merge_sort(right_half)

    return merge(left_half, right_half)

```



### 7. Catalan Numbers



The **Catalan numbers** form a sequence of natural numbers that occur in various counting problems, often involving recursive structures. The recursive formula for the $n$-th Catalan number is 



$$

C_n = \sum_{i=0}^{n-1} C_i \cdot C_{n-1-i}

$$



where the base case is $C_0 = 1$.





## 3. What is the difference between _Backtracking_ and _Recursion_?



**Backtracking** often employs **recursion** to explore the vast space of possible solutions. However, not all recursive algorithms involve backtracking.



Think of **recursion** as the mechanism that enables a function to call itself, and **backtracking** as a strategy where you make a choice and explore the possibilities.



### Key Concepts



- **Recursion**: Utilizes a divide-and-conquer approach, breaking the main problem into smaller, self-similar subproblems. Recursive calls work towards solving these subproblems, relying on defined base cases for termination.



- **Backtracking**: Operates as an advanced form of recursion by building solutions incrementally. When a partial solution is deemed unsuitable, it "backtracks" to modify previous choices, ensuring an efficient traversal through the solution space.



### Common Applications



#### Recursion



- **Tree Traversals**: Visiting all nodes in a tree, like in binary search trees.

- **Divide and Conquer Algorithms**: Such as merge sort or quick sort.

- **Dynamic Programming**: Solving problems like the coin change problem by breaking them down into smaller subproblems.



#### Backtracking



- **Puzzle Solvers**: Solving games like Sudoku or crossword puzzles.

- **Combinatorial Problems**: Generating all permutations or combinations of a set.

- **Decision-making Problems**: Such as the knapsack problem, where decisions are made on whether to include items.





## 4. Define _Base Case_ in the context of recursive functions.



**Base Case** is a pivotal concept in recursive functions, serving as the stopping condition. Without this safeguard, the function can enter an infinite loop, possibly crashing your program.



### Mathematical Representation



In mathematical terms, a function is said to operate **recursively** when:



$$ f(x) = \begin{cases} 

g(x) & \text{if } x \text{ satisfies some condition} \\

h(f(x-1), x) & \text{otherwise} 

\end{cases} $$



And it has a **defined starting point** when $x$ satisfies the **base case** condition.



### Example: Factorial Function



The **base case** typically addresses the smallest input or the simplest problem state. In the **factorial** function, the base case is when $n = 0$ or $n = 1$, with the eventual return value being $1$.



#### Code Example: Factorial



Here is the Python code:



```python

def factorial(n):

    # Base Case

    if n in (0, 1):

        return 1

    

    # Recursive Step

    return n * factorial(n - 1)

```



### Creating the Base Case



1. **Identify the Simplest Problem**: Pinpoint the characteristics of a problem that can be solved directly and quickly without further reduction.

2. **Establish the Stopping Criterion**: Define a condition that, once met, triggers the direct solution without the need for further recursive calls.

3. **Handle the Base Case Directly**: Upon satisfying the stopping condition, solve the problem directly and return the result.



**Tip**: Explicitly stating the base case at the beginning of the function can enhance code clarity.





## 5. Explain the concept of _Recursion Depth_ and its implications on algorithm complexity.



**Recursion depth** refers to the number of times a function calls itself, typically visualized as a call stack.



As functions recursively call themselves, a **stack** of queued, yet-to-complete recursive function calls forms. When the limit of recursive calls is reached or excessive memory isn't available, you encounter a "stack overflow."



### Complexity Implications



The **time** and **space complexities** of an algorithm can be linked to its recursion depth.



#### Time Complexity



- **Best-Case**: The algorithm might have constant time complexity, but if the recursion depth reaches $k$, then the overall time complexity is $O(k)$.

- **Worst-Case**: If the recursion depth is $n$, the time complexity is typically $O(n)$.



#### Space Complexity



- The space complexity is calculated in $O(1)$ or $O(n)$ terms, depending on whether the stack remains bounded by a small constant or grows with $n$, respectively.



### Managing Recursion Depth in Code



1. **Tail-Call Optimization (TCO)**: Certain programming languages optimize tail-recursive calls, ensuring that they don't add to the call stack. This effectively converts a recursive function into an iterative one.

  

2. **Explicit Control**: In some situations, you can avoid or reduce recursion depth by using loops or memoization.



3. **Iterative Alternatives**: Algorithms initially implemented using recursion can often be transformed to use loops instead, circumventing the need for stack memory.





## 6. How does the _Call Stack_ operate in recursive function calls?



**Call Stacks** provide a strategy for tracking active **function calls** and managing **local variables**.



Let's see how the **call stack** operates in the context of recursive functions and go through an example:



### Example: Factorial Calculation



Here is the Python code:



```python

def factorial(n):

    if n <= 1:

        return 1

    return n * factorial(n - 1)



result = factorial(5)

print(result)

```



In the example, `result` will be `120`.



### Call Stack Operations in Recursive Functions



1. **Function Call**: When `factorial` is invoked with `5`, a new frame is created and pushed onto the stack.

  

   ```

   factorial(5)

   ```



2. **Base Case Check**: Upon each function call, the `If` condition checks if `n <= 1`. If it is, the top frame is popped from the stack, and the result is returned, terminating the sequence.



3. **Recursion**: If the base case doesn't apply, the function calls itself with a reduced argument. This "recursive" call is pushed onto the stack:



   ```

   factorial(4)

   ```



   The stack might look like this:

   

   ```

   factorial(5)

   factorial(4)

   ```



4. **Backtracking**: After the base case is met, the call stack starts unwinding and calculating results. This process **unwinds the call stack**, returning the factorial result for each frame in the call sequence.



The call stack for our factorial example will look like this during its lifecycle:



```plaintext

Empty Stack                      



Push factorial(5)  

factorial(5)                   



Push factorial(4)  

factorial(4) -> factorial(5) (top)      



Push factorial(3)   

factorial(3) -> factorial(4) -> factorial(5) (top)  



Push factorial(2)  

factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)  



Push factorial(1)  

factorial(1) -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)  



Push return 1    

return 1 -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)  



Push return 2  

return 1 -> factorial(2) -> factorial(3) -> factorial(4) -> factorial(5) (top)  



Push return 6  

return 2 -> factorial(3) -> factorial(4) -> factorial(5) (top)  



Push return 24  

return 6 -> factorial(4) -> factorial(5) (top)  



Push return 120  

return 24 -> factorial(5) (top)  



Pop Final Factorial  

Empty Stack  

```



After `factorial(1)` returns `1`, each frame multiplies its return value by the respective `n` before returning. This results in the final `120` on top of the stack before being returned and popping all the frames from the stack.





## 7. Are there any safety considerations when determining the _Recursion Depth_? If yes, provide an example.



When dealing with recursion, **excessive recursion depth** can lead to stack overflow errors or, in rare cases, security vulnerabilities.



### Safety Considerations



#### Stack Overflow



Excessive recursion can lead to **stack overflow**, a condition where the program runs out of stack space and crashes. Each recursive call contributes to the stack, and if there are too many calls, the stack can't keep up.



Consider the following Python example, which gets increasingly slower as n grows:



```python

def countdown(n):

    if n <= 0:

        return

    else:

        countdown(n-1)



countdown(10000)  # This will fail

```



#### Real-World Example: affecting a web page's UI



In web development, excessively deep recursion can burden the UI.



Let's say you have a webpage where an onClick event triggers a JavaScript function `handleClick()`. If `handleClick()` makes recursive calls without an exit condition, the browser might stop responding because each function call hogs a portion of the call stack, potentially impacting the entire UI.



#### Security Vulnerability



In a multi-user environment, such as a web server handling multiple client requests, **insufficient resource allocation** for handling recursive calls can lead to resource exhaustion and, in extreme situations, open the door to attacks, like a Denial of Service (DoS).



For example, consider a web server that is designed to execute a recursive algorithm to process client requests. If the server has a strict **limit** on the maximum recursion depth, an attacker could send crafted requests, exploiting the maximum depth and causing the server to crash, rejecting legitimate requests.



#### Resource Exhaustion: Extending the Recursion Example



In the given Python example, you can experiment with higher values for `n` and observe how the program exhausts its resources. 



```python

def countdown(n):

    if n <= 0:

        return

    else:

        countdown(n-1)



# Try with a very high value for n

countdown(1000000)  # Monitor the memory consumption as an illustration

```





## 8. Explain the _Depth-First Search_ algorithm.



**Depth-First Search** (DFS) is a graph traversal algorithm that's simpler and **often faster** than its breadth-first counterpart (BFS). While it **might not explore all vertices**, DFS is still fundamental to numerous graph algorithms.



### Algorithm Steps



1. **Initialize**: Select a starting vertex, mark it as visited, and put it on a stack.

2. **Loop**: Until the stack is empty, do the following:

   - Remove the top vertex from the stack.

   - Explore its unvisited neighbors and add them to the stack.

3. **Finish**: When the stack is empty, the algorithm ends, and all reachable vertices are visited.



### Visual Representation



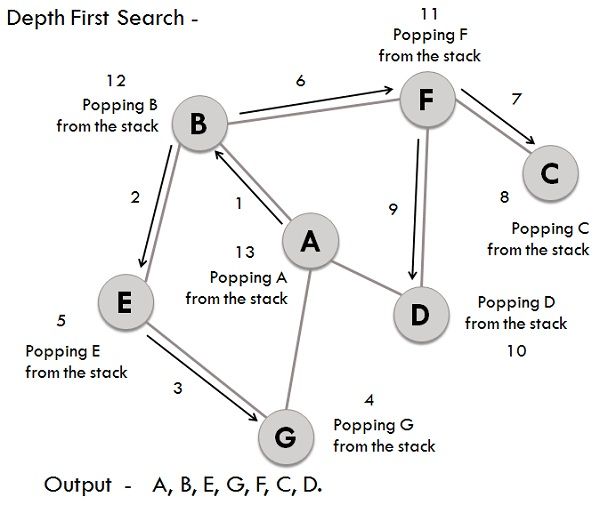
![DFS Example](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/graph-theory%2Fdepth-first-search.jpg?alt=media&token=37b6d8c3-e5e1-4de8-abba-d19e36afc570)



### Code Example: Depth-First Search



Here is the Python code:



```python

def dfs(graph, start):

    visited = set()

    stack = [start]

    

    while stack:

        vertex = stack.pop()

        if vertex not in visited:

            visited.add(vertex)

            stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)

    

    return visited



# Example graph

graph = {

    'A': {'B', 'G'},

    'B': {'A', 'E', 'F'},

    'G': {'A'},

    'E': {'B', 'G'},

    'F': {'B', 'C', 'D'},

    'C': {'F'},

    'D': {'F'}

}



print(dfs(graph, 'A'))  # Output: {'A', 'B', 'C', 'D', 'E', 'F', 'G'}

```





## 9. Implement a _Recursive Algorithm_ to perform a _Binary Search_.



### Problem Statement



The objective is to **write a recursive algorithm** that conducts a **binary search** on an array of $n$ numbers and determines if a specified element $x$ is present.



### Solution



While a recursive solution may not be the most efficient for binary search, as it can lead to stack overflow with long lists, it's essential for practice and understanding of recursion.



#### Algorithm Steps



1. **Base Case**: If the array is empty, return `False`.

2. **Recursive Step**: Inspect the midpoint. If it matches $x$, return `True`. Otherwise, probe the appropriate half of the array based on the comparison of the midpoint value with $x$.



#### Complexity Analysis



- **Time Complexity**: $O(\log n)$ 

- **Space Complexity**: $O(\log n)$



#### Implementation



Here is the Python code:



```python

def binary_search_recursive(arr, low, high, x):

    if high >= low:

        mid = (high + low) // 2



        # If element is present at the middle

        if arr[mid] == x:

            return True

        # Search left subarray

        elif arr[mid] > x:

            return binary_search_recursive(arr, low, mid - 1, x)

        # Search right subarray

        else:

            return binary_search_recursive(arr, mid + 1, high, x)

    else:

        # Element is not present in array

        return False

```





## 10. Solve the _Tower of Hanoi_ problem recursively.



### Problem Statement



The Tower of Hanoi puzzle consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with all disks stacked in _increasing_ sizes on the first rod in ascending order, with the smallest on top. The objective is to move the entire stack to the last rod following these rules:



1. Only one disk must be moved at a time.

2. A disk must never be placed on top of a smaller disk.



### Solution



The Tower of Hanoi puzzle can be elegantly solved using **recursion**. By assuming you have a function `hanoi` to handle moving disks from one peg to another, you can construct the recursion.



#### Algorithm Steps



1. Move `n-1` disks from the start peg to the extra peg, using the destination peg as the temporary peg.

2. Move the remaining largest disk from the start peg to the destination peg.

3. Move the `n-1` disks from the extra peg to the destination peg, using the start peg as the temporary peg.



#### Complexity Analysis



- **Time Complexity**: $O(2^n)$. Although each disk is only moved once, the pattern of recursive calls results in an exponential number of moves.

- **Space Complexity**: $O(n)$ due to the function call stack.



#### Implementation



Here is the Python code:



```python

def hanoi(start, dest, extra, n):

    if n == 1:

        # Base case: move the smallest disk

        print(f"Move from {start} to {dest}")

        return

    # Move n-1 disks to the extra peg

    hanoi(start, extra, dest, n-1)

    # Move the largest disk to the destination peg

    print(f"Move from {start} to {dest}")

    # Move the n-1 disks from the extra peg to the destination peg

    hanoi(extra, dest, start, n-1)



# Test the function with 3 disks

hanoi('A', 'C', 'B', 3)

```





## 11. Recursively _Check for Palindromes_ in a string.



### Problem Statement



The task is to **determine** whether a given string, $s$, is a **palindrome**.



#### Example



- $s = \text{"radar"}$: Palindrome

- $s = \text{"hello"}$: Not a palindrome



### Solution



We can solve this **recursively** by comparing characters from the start and end of the string.



#### Algorithm Steps



1. **Base Case**: For strings of length 0 or 1, return true.

2. **Recursion Step**: Compare the first and last characters. If they are equal, check if the substring between them is a palindrome.



#### Complexity Analysis



- **Time Complexity**: $O(n)$ where $n$ is the string's length. This is due to the $n/2$ comparisons made in each recursive call.

- **Space Complexity**: $O(n)$ due to the recursive stack.



#### Implementation



Here is the Python code:



```python

def is_palindrome(s):

    s = s.lower()  # convert to lowercase to handle cases like "Aa"

    if len(s) <= 1:

        return True

    if s[0] != s[-1]:

        return False

    return is_palindrome(s[1:-1])



# Test the function

print(is_palindrome("radar"))  # Output: True

print(is_palindrome("hello"))  # Output: False

```





## 12. Explain the process of performing a recursive _In-order Tree Traversal_.



The **in-order** tree traversal, often referred to as the "left-root-right" traversal, is a classic example of recursion in action. It involves visiting nodes in a binary tree in a specific order.### Traversal Steps



1. **Visit the Left Subtree**: Recursively traverse the left subtree.

  

2. **Visit the Root Node**: The node where traversal starts.

  

3. **Visit the Right Subtree**: Recursively traverse the right subtree.



### Visual Representation



![In-Order Traversal](https://firebasestorage.googleapis.com/v0/b/dev-stack-app.appspot.com/o/data%20structures%2Finorder-traversal.png?alt=media&token=6866cf58-b446-4b40-9781-5b04698eb0e0)



### Code Example: In-Order Traversal



Here is the Python code:



```python

def in_order_traversal(node):

    if node:

        in_order_traversal(node.left)

        print(node.data)

        in_order_traversal(node.right)

```





## 13. Calculate _N-th Fibonacci Number_ using _Tail Recursion_.



### Problem Statement



The task is to **compute** the $n$-th Fibonacci number using the **tail recursive** method.



### Solution



**Tail recursion** offers an optimized approach to compute the Fibonacci series. In this method, the function updates parameters and makes a **single recursive call** as its last operation, effectively transforming the **recursion** into a **loop**.



#### Core Logic



The function utilizes two accumulators, `a` and `b`, to store Fibonacci values and recursively computes the series.



#### Complexity Analysis



- **Time Complexity**: $O(n)$ 

- **Space Complexity**: $O(1)$ due to the optimized call stack. It suitable for larger values of $n$.



#### Implementation



Here is the Python code:



```python

def fib_tail(n, a=0, b=1):

    if n == 0:

        return a

    return fib_tail(n - 1, b, a + b)

```







## 14. Discuss how _Tail Recursion_ can be optimized by compilers and its benefits.



**Tail call optimization** (TCO) is a compiler feature that promotes **efficient memory usage** in languages like Erlang, Haskell, and Scheme. It does so by converting certain types of recursive functions, known as "tail-recursive calls," into a looping structure, rather than employing a traditional call stack.



### Optimizing Memory Allocation



- **Traditional Recursion**: Each function call uses stack memory, which can lead to stack overflow if the depth of recursion is too high.



- **Tail Recursion with TCO**: The compiler reuses the same stack frame and can, in some cases, eliminate the need for stack memory altogether.



### The Mechanics of Tail Call Optimization



- **What is a Tail Call?**: A function call is a tail call if it's the last operation before the current function returns. 



- **When Does TCO Occur?**: The compiler applies TCO when it recognizes tail calls, ensuring the recursive function doesn't leave any work to be done after the recursive call.



- **Comparing Tail Calls**: In non-tail-recursive calls, the returned value and any other operations often require further processing by the calling function, which isn't the case for tail-call-optimized functions.



### Code Example: Non-Tail Recursive vs. Tail-Recursive with TCO



Here is the Ruby code:



```ruby

# Non-tail-recursive function

def factorial_non_tail(n)

  return 1 if n == 0

  n * factorial_non_tail(n - 1)

end



# Tail-recursive function

def factorial_tail(n, accumulator = 1)

  return accumulator if n == 0

  factorial_tail(n - 1, n * accumulator)

end

```



### Compiler Support for TCO



While TCO might not be guaranteed in languages like Java or C++, many modern compilers extend this feature to support both tail-call optimized and general tail-recursive functions.



### Practical Usage



- **Real-World Example**: The Mars Rover Kata demonstrates TCO. A primary advantage is that it helps in managing program state.



- **Safe for Large Inputs**: Tail call-optimized functions allow for safe handling of large inputs, which can be especially beneficial in domains like scientific computing or data processing.



- **Discreet Implementation**: Shepherd resource usage by keeping the call stack more compact.



- **Functional Programming**: It is especially relevant to functional programming styles, where recursive definition is common.





## 15. What is the difference between _Head Recursion_ and _Tail Recursion_?



Let's explore the concepts of **Head Recursion** and **Tail Recursion**.



### James Bond Comparison



- **Head Recursion**: Like James Bond, it gets "right to the action," leaving the "clean-up" for last.

- **Tail Recursion**: Follows actions on the "go," much like James Bond racing through an action scene.



### Practical Example



Suppose you, as Bond, need to navigate a maze, represented as a sequence of instructions (each with a code name), and perform specific actions:



1. **Head Recursion**: Upon finding an instruction, Bond plans to apply it to the next target in the endless sequence. He first solves the whole maze, recording the actions needed, and then executes the actions in the reverse order.

2. **Tail Recursion**: When Bond first locates an instruction, he adapts it to the current target and then hastens to the next location, repeating this process until he reaches the end of the maze or finds a better course of action.



Bond covertly records his actions as a strategist provides instructions to demonstrate each technique.



#### Maze Nav: Head Recursion



```plaintext

Maze Sequence: A -> B -> C -> D

Action Order: Left (A), Left (B), Left (C), Left (D)



James Bond: "I'll analyze the entire sequence initially and follow it step-by-step, but in reverse."

```



#### Maze Nav: Tail Recursion



```plaintext

Maze Sequence: A -> B -> C -> D

Action Order: Left (A)



James Bond: "I'll adapt my actions at each point, operating in real-time for the best outcome."

```



### Recursion



Both **Head** and **Tail Recursion** strategies frequently employ recursive functions, which call themselves to process smaller segments of data.



- The head-recursive method affixes its adversarial "action" before the recursive call, leaving the "clean-up" for the resolve phase.

- The tail-recursive function "deal with the mess" before the recursive invocation, ensuring a smoother operation with each iteration.



### Code Example: Head Recursion



The Bond agent will navigate the maze as shown:



```plaintext

A -> B -> C -> D

```



Here is the Python code for the Head Recursion:



```python

def head_recursion(maze_sequence, action_order):

    if maze_sequence:

        head_recursion(maze_sequence[:-1], action_order)  # Recursive call

        action_order.append(f"Left {maze_sequence[-1]}")  # Action before call



# Initial setup

maze_sequence = ["A", "B", "C", "D"]

actions = []

head_recursion(maze_sequence, actions)

print(actions)  # Expected: ["Left A", "Left B", "Left C", "Left D"]

```



### Code Example: Tail Recursion



The Bond agent navigates the maze as:



```plaintext

Arrives at A, action: "Left A", move to B

Arrives at B, action: "Left B", move to C

Arrives at C, action: "Left C", move to D

Arrives at D, action: "Left D", end of maze

```



Here is the Python code for Tail Recursion:



```python

def tail_recursion(maze_sequence, action_order):

    if maze_sequence:

        action_order.append(f"Left {maze_sequence[0]}")  # Action before call

        tail_recursion(maze_sequence[1:], action_order)  # Recursive call



# Initial setup

maze_sequence = ["A", "B", "C", "D"]

actions = []

tail_recursion(maze_sequence, actions)

print(actions)  # Expected: ["Left A", "Left B", "Left C", "Left D"]

```





#### Explore all 53 answers here 👉 [Devinterview.io - Recursion Algorithm](https://devinterview.io/questions/data-structures-and-algorithms/recursion-algorithm-interview-questions)









data-structures-and-algorithms