Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/gabboraron/biostatisztika_es_alkalmazasai

"A statisztika a matematika azon ága, melynek feladata, hogy eszközt adjon a politikusok kezébe, mellyel tetszőleges állítás és annak ellentéte is tudományos alapon igazolható"
https://github.com/gabboraron/biostatisztika_es_alkalmazasai

biostatistics data-analysis data-visualization r statistics statistics-course

Last synced: 5 days ago
JSON representation

"A statisztika a matematika azon ága, melynek feladata, hogy eszközt adjon a politikusok kezébe, mellyel tetszőleges állítás és annak ellentéte is tudományos alapon igazolható"

Awesome Lists containing this project

README 

        
# Biostatisztika és alkalmazásai

- [Ferenci Tamás YouTube](https://www.youtube.com/c/FerenciTam%C3%A1s/videos)

- [Ferenci Tamás - Bevezetés a biostatisztikába](https://tamas-ferenci.github.io/FerenciTamas_BevezetesABiostatisztikaba/deskriptiv.html#deskriptivaltalaban)

- [Solymosi Norbert -  R - Erre könyv - pdf](https://cran.r-project.org/doc/contrib/Solymosi-Rjegyzet.pdf)



Számonkérések:

- 1 db beadandó - szorgalmi utolsó napjáig

- 1 db zh - félév felénél kb

- írásbeli vizsga



8:20-kor kezdünk - kivéve első három héten



## EA1 - R ismétlés - Statisztika alapfogalmai áttekintés

### Statisztika alapfogalmai áttekintés

- **valségszámítás -> statisztika -> alkalmazott stat ágak**

- **bioinformatika:** inkább számítástechnikai kérdések, nagy adatbázisokon hatékony algoritmikus megoldások

- **biomatematika:** inkább nem statisztikai elsősorban analízisbeli modellezési eszközök, diffegyenletek haszálata



**milyen alapokra van szükség:**

- valségszámítás, linalg

- mat stat

- orvosi ismeretek



**stat programcsomagok:**

- SAS - gyógyszeripar kedveli

- SPSS - Általános célú stat programcsomag szociológusoknak

- R - kalsszikus akadémiai programcsomag



**demonstratív kérdések:**

- egy új vérnyomáscsökkentő csökkenti-e a vérnyomást

  - nem okoz epilepszia-kockázatot?

- milyen tényezők hatnak adott rákban a túlélési időre?

- mennyi jelen kurzus hallgatóinak átlagos testtömege?



**definíciók:**

- **véges sokaság - populáció**: egzakt halmaz amire a kérdésünk irányul: *mennyi jelen kurzus hallgatóinak átlagos testtömege?*

  - **fiktív végtelen sokaság**: nem névszerint felsorolható, de körülírható jellemzőkkel rendlekező halmaz, `eloszlás`al megadott érték

- **megfigelési egység**: a populáció elemei

- **változó/ismérv**: a változó értékének meghatározása egy adott sokasági elemre: megfigyelés <- az összes elem nagyon ritkán megfigyelhető

- **mintavételes helyzet**: általában *nem* tudjuk a teljes sokaságot megfigyleni, de a mgefigylehető része a **minta**

- **induktív statisztika**: hogyan tudunk következtetni az egész sokaságra? *pl: hogyan mondható meg 100 szám átlaga ha csak 99-et ismerek?**

- **deskriptív statisztika**: a statisztika azon fejezete ami nem törődik a mintavétellel

- **proxy változók**: *pl: mekkora a szocio-ökonomia értéke valakinek - kereset, társadalmi státusz, stb-?



#### mérési skálák/adatok jellemzői:

> mi az a művelet amit érdemes elvégezni?

- Stevens 1946:

  - minőségi változó:

    - **nominális skála:** egy ismérv nominális skálán van mérve, ha két megfigyelési egységgel nem ugyanazt az értéket veszik fel. *pl: szemszínek: egyik barna, másik kék, akkor nem adható hozzá átlág, stb...*

    - **ordinális skála:** a nominális + értelmezett, hogy ***melyik nagyobb*** *pl: egy közgáz bsc és egy orvosi MD foknál egyik nagyobb, de semmi köze egymáshoz*

  - mennyiségi változó:  

    - **intervallum skála:** a ***különbségnek*** is van értelme. *pl: Aladár testhőmérséklete 40, Béla 38: egyik nagyobb - másik kisebb; kivonhatóak egymásból; de Aladár hőmérsékletének semmi köze Béláéhoz*

    - **arányskála:** van értelme az ***osztásnak*** is. *pl: Aladár 50 kg, Béla 80 kg, akkor egyik nagyobb, A és B nek nincs köze egymáshoz, de mondható, hogy B x %-al nagyobb*



- **Diszkrét változó:** a kimenetek száma egy diszkrét halmaz: véges/megszámlálhatóan végtelen, *pl szemszín* a nominális és ordinális változók diszkrétek

- **folytonos változó:** kontinuum számosságú, *pl: testhő*, a mennyiségi változók folytonosak



***kivétel:** hányszor volt infarktusod?*



- időbeli jelleg:

  - **keresztmetszeti**: egy időpontban mértünk, nincs utánkövetés 

  - **longitudinális / hosszmetszeti / panel adat**: egymás után többször mértük le, az alanyoknak időbeli követése is van; cohort; eset kontrol;



- **prevalencia**: hányan vannak? - *stock jellegű*

- **incidencia**: hány új valami van? - *flow jellegű*



## R ismétlés

Egy running example-t használunk a félév során



- Birth Weight adatbázis (1986): hogyan prediktálható az újszülött születési tömege? 

  - keresztmetszeti adatbázis



gyerek születési tömege (g): `alacsoy < 2500 `



## gyak 2 - R ismétlés

https://www.w3schools.com/r/



fájl: [biostat_gy_2.r](https://github.com/gabboraron/biostatisztika_es_alkalmazasai/blob/main/biostat_gy_2.r)



- értékadás: `valtozo <- erteke`

- utolsó futási eredmény visszkaérése: `.last.value`

- függvények: `fuggveny(argumentum)`



- az R egy gyengén típusos nyelv



```R

szam <- 3.3

typeof(szam)

str(szam)



egesz <- 3

typeof(egesz)

egesz <- 3L

typeof(egesz)

str(egesz)



beagyazott <- "És Ferenci mondta: 'talpra haza'"



logikai <- TRUE

str(logikai)



logikai <- F

str(logikai)



szovegvektor <- c("alma", "fa")

``` 



típus tesztelése 

```R

is.character()

is.numeric()

is.integer()

is.double()

```



típuskényszerítés

```R

as.character(szam)

as.numeric("2.8")

as.numeric(TRUE)

as.numeric(FALSE)

as.logical(0)

as.logical(1)

as.logical(100)

as.logical(-10)



miafranc <- as.logical(-3.14)

```



### adatszerkezetek

> vektor

> - homogén

> - 1D

> - minden eleme ugyanolyan típusú



```R

szamvektor <- c(2,3.5,6,-4)

szamvektor

str(szamvektor)

```



pl: véletlen szám generálása `rnorm(darabszam)`



Az R-ben nincs skalár, csak egy elemű vektor.

```R

szam <- 5

c(szam,4)



seq(1, 13, 2)

seq(1, 13, 1)



1:13



szamvektor <- c(elso = 3, masodik =8.3, harmadik = -4)

szamvektor["elso"]

```



kulcsok lekérése kulcs-érték párokból álló vektorból: `names(szamvektor)`



```R

##indexelés

szamvektor[3]

szamvektor[c(1,4)]

szamvektor[c(T,T,F,F,T)]

szamvektor[c(T,F)]

szamvektor[-3]



szamvektor[2] <- 10.5

szamvektor

szamvektor[10] <- 20

szamvektor



szamok <- c(1,2,3,4,5)

str(szamok)



valami <- c(NA, NA, NA)

str(valami)

```



mátrix

```R 

### matrixok

szammatrix <- matrix(1:8, nc = 2)

szammatrix

szammatrix <- matrix(1:8, nr = 2)

szammatrix

szammatrix <- matrix(1:8, nc = 2, byrow = TRUE)

szammatrix



dim(szammatrix)

nrow(szammatrix)

ncol(szammatrix)



szammatrix[1,1]



colnames(szammatrix) <- c("egy", "ketto")

rownames(szammatrix) <- c("a", "b", "c", "d")

szammatrix



# több dimenziós mátrix az array

```



dataframe

- 2D

- heterogén (egy oszlopon belül homogén!

- rectangular

```R

adatkeret <- data.frame(elso = c(1,3.4,-3),

                        masodik = c("a", "b", "c"),

                        harmadik = c(T,T,F))

adatkeret

str(adatkeret)



adatkeret[c(T,F,T), -1]



adatkeret$elso

adatkeret[,"elso"]



adatkeret$elso>0.5

adatkeret[adatkeret$elso>0.5,]

```



***a vesszőt nem szabad elfelejteni az indexeléshez!!***



minta adathalmazunk

```R

data(birthwt, package = "MASS")

str(birthwt)

birthwt[str]

colnames(birthwt)



birthwt$bwt    # vektornak adja ki



birthwt[[10]]  #

birthwt["bwt"] # megőrzi a dataframeségét

```



## EA-GY 3

helpet `?parancsnév` vagy `??` ha nem ismerjük a parancs nevétkérhetünk



függvényeknél az argumentumok  nevei elhagyhatóak, pl `rnorm(10,70,15)` és `rnorm(n=10, mean = 70, sd = 15)` ugyanaz; de az ajánlás szerint a jobb olvashatóság kredvéért érdemes megadni a neveket!



ciklusok helyett `apply` fv család



```R

# lapply(elem_amire_függvényt_hívunk, függvény)

lapply(1:3, rnorm)

```



feltételes

```R

birthwt$ht <- birthwt$ht == 1

```



***packagek:*** 

```R

install.packages("psych")

psych::describe(birthwt)

library(psych)

```

bővebben: [gy3.r](https://github.com/gabboraron/biostatisztika_es_alkalmazasai/blob/main/gy3.r)



- beadandót R markdownban kell csinálni



- Alulsímitott a megoldás, ha túl nagy súlyt adunk annak, hogy szép legyen a görbe, azaz az intervallumokat túl nagynak választjuk.

- túlsímított a megoldás, ha normlisok szélessége *sávszélesség* túl kicsinek van választva és hisztogram szerű "képet" kapunk



A sávszélességet a sűrűségtől tesszük függővé, hogy optimálisabb becslést adjunk a sűrűségfüggvényhez,`kde` témakörben van több róla. A magfüggvény azt is befolyásolhatja, hogy mit teszünk rá: háromszögeket, téglalapokat (egyenletes eloszlás), matematikai optimalizációs megoldások.



***Ahol lehet próbáljunk magfüggvényes becslőt használni, mert jobb mint a hisztogram.***



bővebben a magfüggvényes becslésről: https://gyires.inf.unideb.hu/KMITT/a04/ch09s03.html



### kétváltozós elemzés



centrális tendencia - középérték

- átlag

- mértani átlag <- *komplikáltabban még nem láttam az átlagot elmagyarázva*

  a logaritmusok átlagának exponenciáltja a mértani átlag

  a logaritmikusan lehet gyorsan szorozni

- trimmelt átlag / nyesett átlag `mean(birthwt2$bwt, trim = 0.05)` A `trim` optimális értéke attól is függ, hogy mennyi adatunk van az adathalmazban. A `trim` az egyik oldalra értlemezhető érték, tehát a maximumot két oldalról nézve 0,5 és nem 1!

  A trim adatvesztés!!

- **medián:** nagyság szerint sorbarendezett elem közül a középső *(páros sok elemnél is értlemzhető, különböző szabályokkal)* => az elemek fele kisebb nála, az elemek másik fele meg nagyobb. *Az egyenlő esete definíció kérédse, bővebben `?quantile`* A medián robosztus az outlaierekre.

  A medián az összes többi értéket figyelmen kívűl hagyja, tehát olyan mint egy trim. 



*Ha a változónál nincs értelme az összegnek akkor az átlagnak sincs!*



Ha x_i -> \infinitry akkor az átlag is tart a végtelenbe!



**adatgeneráló folyamat:** az a mechanizmus ami kiköpi az értékeket. Pl a mérés.



- lognormális eloszlás: az az eloszlás aminek az eloszlása normális

- *`p`*edelő pont: az elemek `p`ed része kisebb nála, és `p`ad része nagyobb.

  kvantilis: `quantile(bwt, 0.6)`

  kvartilis: `quantile(bwt)` azaz a negyedek

  tizedek: `quantile(bwt, seq(0.1, 0.9,0.1))`

  

  

### boxplot

> ![what is boxplot](https://miro.medium.com/max/1400/1*2c21SkzJMf3frPXPAR_gZA.png) ![boxplot agrafikonhoz képest](https://miro.medium.com/max/1400/1*NRlqiZGQdsIyAu0KzP7LaQ.png)

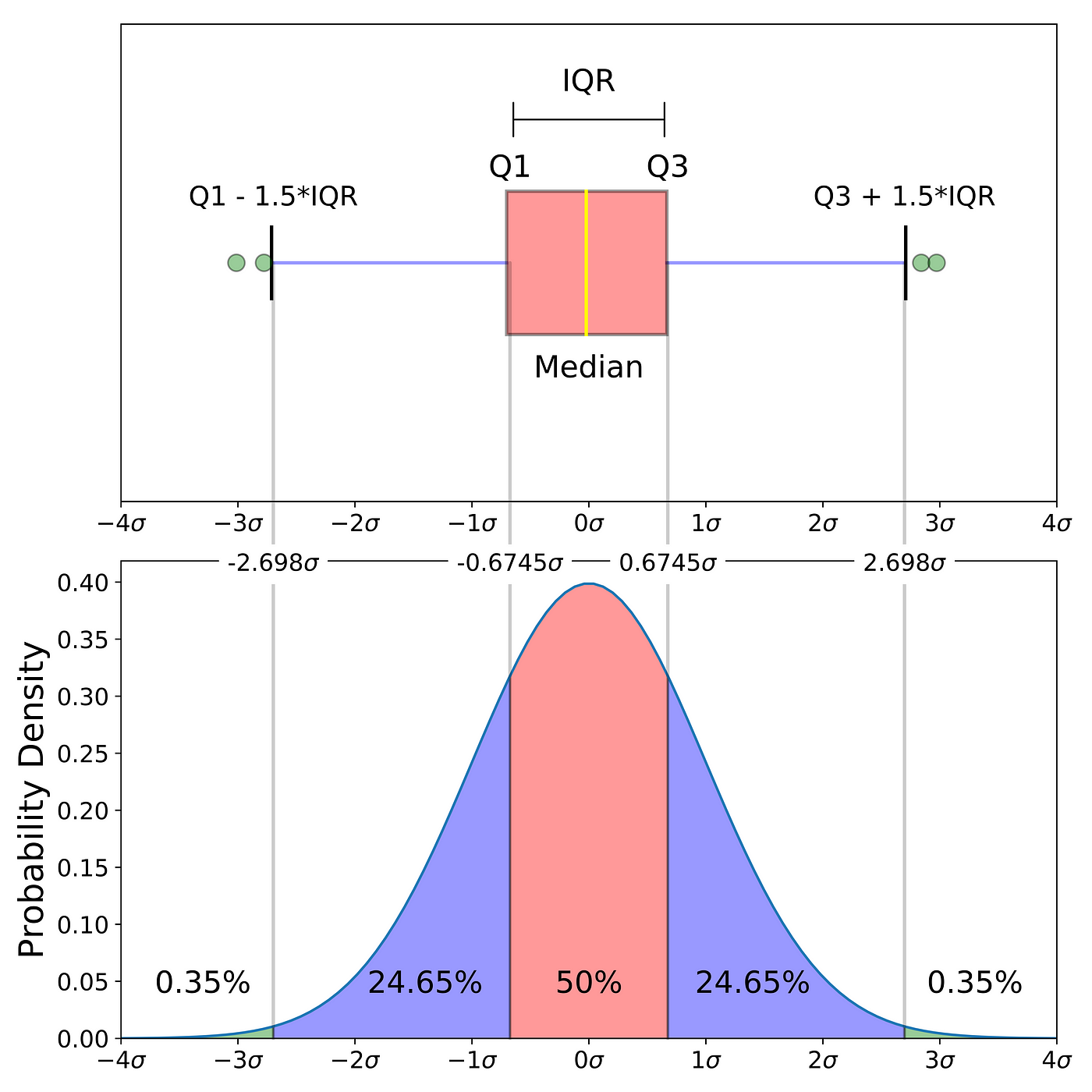
> A doboz része q1-q3 ig tart, a központi vonal a medián. Az alsó kilógás az outlaier nélküli minimum, a felső az outlaier nélküli maximum.

>

> A kvartilisek közti terjedelem az iqr.

>

> Az outlierek a kiugró értékek.



bővebben: [biostat_gy_5.R](https://github.com/gabboraron/biostatisztika_es_alkalmazasai/blob/main/biostat_gy_5.R)



## EA - GY4

**ápr 5 zh!!**



a kétváltozós vizsgálat lehetővé teszi a változók közötti kapcsolattermetést is



kontingencia tábla *(ez a gyakorisági sor 2D verziója)*

```R

table(birthwt$race, birthwt$ui)



#                0  1

#  kaukazusi    83 13

#  afroamerikai 23  3

#  egyeb        55 12

```

bővebben: https://hu.wikipedia.org/wiki/Kontingenciat%C3%A1bl%C3%A1zat



ahol a **gyakorisági sor** a sorösszegekből áll össze ezt az alábbi módon is megkaphatjuk:



```R

margin.table(table(birthwt$race, birthwt$ui), 1)

```



***Tehát, a két változós vizsgálatban minden benne van ami az egy dimenziósban is!***



- **relatív gyakoriság**: minden számot leosztunk valamennyivel `prop.table(table(birthwt$race, birthwt$ui))`

- **feltételes eloszlás**: mikor a táblázat minden elemét elosztjuk a sorösszeggel.

  ```R

  # mennyi a gyakoriság adott betegségnek rasszok mentén

  prop.table(table(birthwt$race, birthwt$ui), 1) # 1 - sorok

                                                 # 2 - oszlopok

  ```



A tényleges kontingencia tábla mennyire van messze attól amit a változók között kapcsolat mond?

- ha nincs összefüggés és függetlenek lennének akkor a *gyakorisági sor*t vesszük alapul

- ha [függetlenek](https://hu.wikipedia.org/wiki/Felt%C3%A9teles_val%C3%B3sz%C3%ADn%C5%B1s%C3%A9g) lennének akkor annak a ***relatív gyakorisága*** annak a aavalsége, hogy *valaki afroamerikai és beteg, azt úgy kapjuk meg, hogy összeszorozzuk anank a valségét, hogy afroamerikai annak a valségével, hogy beteg.*

  ```R

  # függetlenség esetén várt adatok amiket összevetünk a ténylegessel

  tabe <- outer(prop.table(table(birthwt$race)),

         prop.table(table(birthwt$ui)))

  tabe

  sum(tabe)

  tabo <- tabe*nrow(birthwt)

  

  #tényleges adatokkal összevetve minnél messzebb van annál jelentősebb a kapcsolat

  ```

- az összefüggést az adja meg ***milyen messze van valami*** azaz, ehhez adott egy távolság metrika

  Ez a [khí négyzet stat](https://hu.wikipedia.org/wiki/Kh%C3%AD-n%C3%A9gyzet_pr%C3%B3ba) 

  ```R

  chisq.test(birthwt$race, birthwt$ui)

  ```



- összefüggést látunk egy két dimenziós khí négyzet táblázatban *pl: mi a kapcsolat a szocio-ökonómiai státusz és a végzettség között*

  - az origó a bal felső sarokban van

  - a kapcsolat iránya

    - pozitív kapcsolat a mellékátlón alakul ki

    - negatív kapcsolat az ami a főátlón alakul ki

  - a kapcsoalt erősségét az összefüggés mértéke adja meg

  ![khi négyzet táblázat](https://titan.physx.u-szeged.hu/tamop411c/public_html/HU%20-%20Optikai%20alapok%20az%20ELI-ALPS%20t%C3%BCkr%C3%A9ben%20II.%20-%20PhD%20(e-learning)/m1_Dia16.3.PNG)



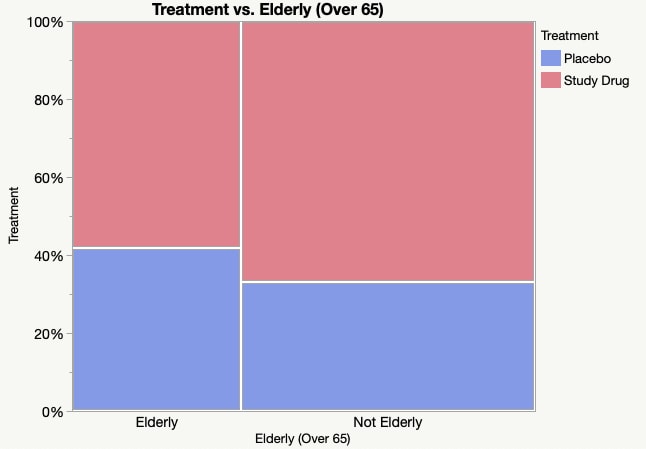
> ### mosaic plot

> akkor nincs kapcsolat ha az elválasztó vízszintes vonal folytatólagos

> ![mosaic plot](https://www.jmp.com/en_us/statistics-knowledge-portal/exploratory-data-analysis/mosaic-plot/_jcr_content/par/styledcontainer_2069/par/image_781608853.img.png/1597772702665.png)



```R

plot(birthwt$lwt, birthwt$bwt)

```



Az k szerinti átlag: `xa` y szerinti átlag: `ya` ezért `(xi-xa)(yi-ya)` szorzat értéke megadja, hogy a pont pozitív vagy negatív kapcsolatot ad meg. Ebből adódoan ha ezeket összeadjuk és leosztjuk `n-1`-el akkor az egész adathalmazra kapunk egy értéket. Ez a ***kovariancia***. `cov(birthwt$lwt, birthwt$bwt)`

- ebből leolvassuk az előjelet: a kapcsolat irányát

- nagy a szórás: nagy a szám => a covariencia mindig +/- két szórás között van =>  `cov(x,y)/sx*sy` ez mindig `+1` és `-1` között van, ez a ***korreláció***

  - szintén értelmezett az előjel 

  - van értlemezhető nagyság fogalom [-1;1] skálán, de ezt az értéket abszolút értékben vehetjük

  - megadja mennyire illeszkednek a rájuk legjobban illeszkedő egyenesre. -> lineáris korrelációs eggyüttható => `+1` ha nagyon illeszkedik rá.



bővebben: [biostatgy4.R](https://github.com/gabboraron/biostatisztika_es_alkalmazasai/blob/main/biostatgy4.R)



minnél szorosabban illeszkednek az egyenesre annál közelebb van a korrelációs eggyüttható az egyhez, minnél nagyobb a szórás annál inkább van közel a 0-hoz. Mivel egy egyeneshez való  távolságot nézzük ezért mondhatjuk, hogy lineáris kapcsolatot mér két változó között. Konkrétan determinisztikus kapcsolatot is 0-nak láthatunk, ha a görbe nem egy egyenes! => érdemes nagy információ sűrítő metrikák használata előtt az adatokat megvizsgálni. De van olyan *(spearman féle ró és tau)* ami több féle görbére méri az erősségét. *Pl: egy parabolára ha illeszkedik, akkor a lineáris korrelációja 0, és nem 1, de a spearman féle rója magas lesz.* 



*pl:*



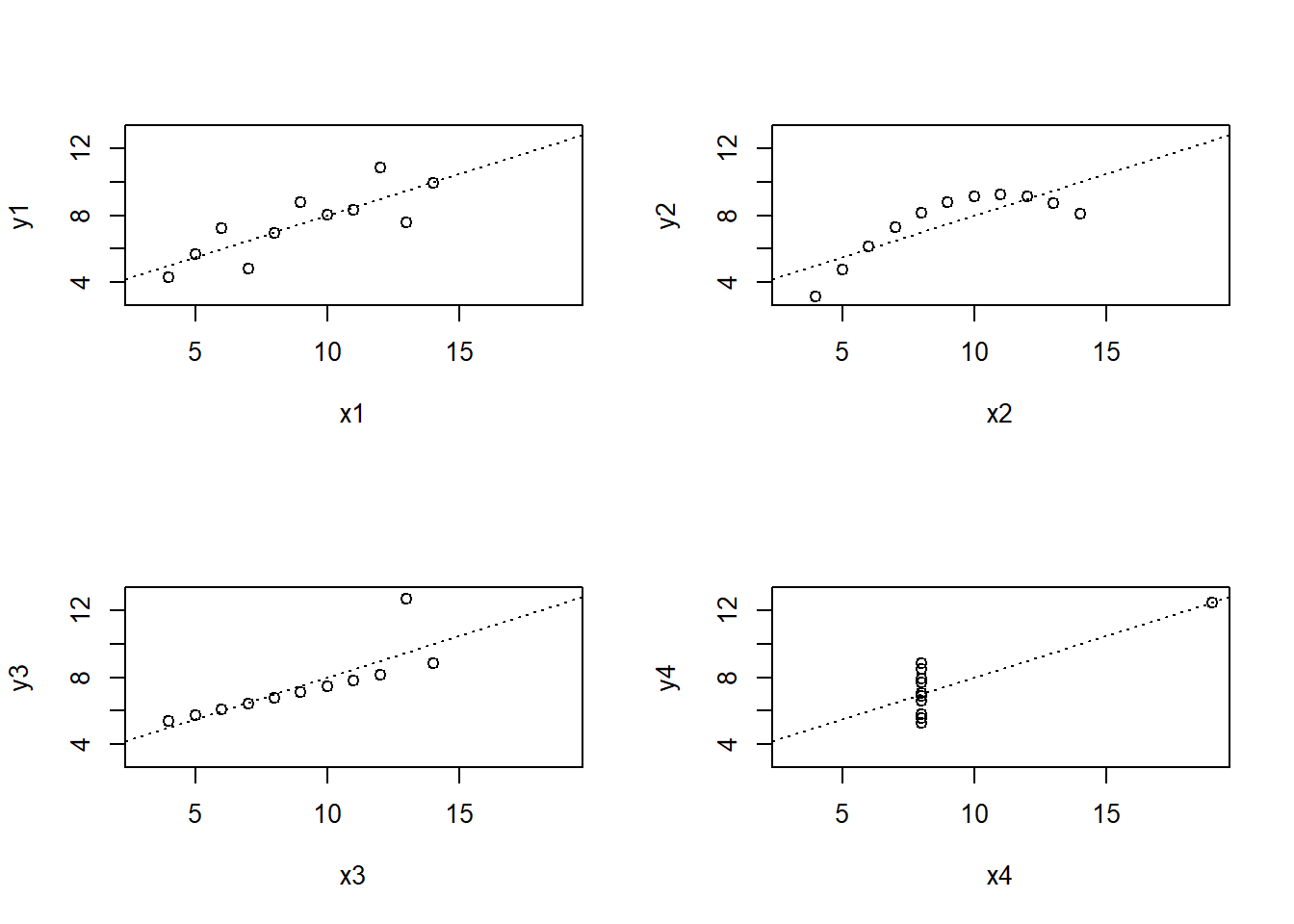
![Az Anscombe-kvartett. ](https://tamas-ferenci.github.io/FerenciTamas_BevezetesABiostatisztikaba/FerenciTamas_BevezetesABiostatisztikaba_files/figure-html/anscombe-1.png)



## R markdown

- https://pandoc.org/



`Knit`-re kattintva fordít!!



legördülőben kiválasztjuk, hogy mire



## Induktív statisztika

https://tamas-ferenci.github.io/FerenciTamas_BevezetesABiostatisztikaba/induktiv.html



> ## ZH készülés

> ### 1. Ismertesse egy kategoriális változó vizsgálatára szolgáló grafikus módszereket!

> Használhatunk kör és oszlopdiagrammot. Az oszlopdiagram jobb az emberi szem számára. Ha oszlopdiagramm akkor lehet Hisztogram is,illetve az alapján magfüggvényes becslés. A sűrűségfüggvényt [becsülhetjük](https://backhauszagi.web.elte.hu/gyak/sst_st4ea_k/sst_st4ea_k2.pdf) téglalapos, háromszöegs és Gauss magfüggvényel valamint Parzen Rosenblatt módszerrel is. Hasonlóan jó módszer lehet a boxplot is, amivel egyszerre láthatjuk a szórást a mediánt, a minimumot és a maximumot is.

>

> ### 2. Ismertesse egy folytonos változó vizsgálatára szolgáló analitikus módszerek közül a középértékre (centrális tendencia) vonatkozó mutatószámokat!

> - medián: mikor sorbarendezzük az elemeket és kivesszük a középső elemet, így tőle jobbra és tőle balra ugyanannyi elem található. Az így kapott elemet pedig tekinthetjük egy átlagnak a nagysága alapján.

> - trimmelt átlag: levágjuk a bizonyos, előre meghatározott szempont szempont szerint túlságosan "kilógó" elemet. Ekkor mindkét irányból ugyanannyit vágunk le!

> - mértani átlag: a logaritmusok átlagának exponenciáltja

>

> ### Mit nevezzünk robusztusságnak? Mondjon példát robusztus és nem robusztus mutatóra a szóródást mérő mutatószámok közül!

> robosztus pl a medián ami figyelmen kívűl hagjya az outliereket, így azokra nézve robosztus. Általánosságban elmondahtó, hogy robosztussgának ezt nevezhetjük, ha minnél több tulajdonságot, paramétert figyelmen kívűl hagyva is helyesen működik az adot eljárás. Nem robosztus például épp ezért az átlag avagy a szmtani közép az outlierekre, mivel bele kalkulálja azokat is  a végső értékbe.

> 

> ### Mit mér a szokásos korrelációs együttható? Hasonlítsa egymáshoz a kovarianciát és a korrelációt a gyakorlat szempontjából!

> A covareiencia egy pont távolságát adja meg khí nétgyzettel, két változó szorzatának várható érétkével. Ha ezeket összeadjuk és leosztjuk `n-1`el akkor a szórások között kapjuk meg az érétket. Ha ezt transzformáljuk [-1,1] intervallumra akkor az a korreláció.



## induktív statisztika

törődünk a mintavétellel



hogyan tudok a minta kis részhalmazából a teljes egészre következtetni?



sokaság átlaga ha érdekel minket.



Csak becsléseket tudunk mondani, amivel nagy hiba és bizonytalanság van a végeredményben.



- Θ a minta sokasága. A sokaságot leírja a szórás és az átlag.



A sokaság eloszlása normális, ekkor a normális eloszlás.



A sűrűségfüggvény becsléssel, hisztogrammal egy nempraméteres sűrűségbecslő. 



`X ~ *N*(μ, ρ 0)` normális eloszlást küövető sokaság.

minta nagyságot minidg `n`el jelöljük: X1, X2, ..., Xn (**f**üggetlen **a**zonos **e**loszlású)



`θ^ = f(X1, X2, ..., Xn)` becslőfüggvény



Ha egy konkrét mintánk van akkor nem tudjuk megvizsgálni azokat a tulajdonságait, amivel azt nézzük, hogy mennyire van közel a valósághoz. Ha viszont valváltozókkal vesszem (újra és újra veszem az értéket és kiszámolom rá az átlagot) ez a mintavételi eloszlsás. Ennek a szórása nem nulla. 



Ez mintáról-mintára változik!



Ha egy becslőfüggvény várható értéke (eloszlás) megegyezik a mintavétel várható étékével akkor torzítatlannak tekintjük. Ha különbség van akkor a különbség értéke adja meg a torzítás mértékét (BIAS).



Két torzítatlen becslő közül az a hatásosabb amelyiknek kisebb a mitavételi szórásnégyzete.



Egy becslő standard hibája a mintavételi szórás eloszlása `sd(simDes)`



-minden torzítatlan becslőre megy



*bővebben: [gyak6.r](https://github.com/gabboraron/biostatisztika_es_alkalmazasai/blob/main/gy6.R)*



# biostat gy 7 - pontbecslés

> induktív következtető statisztika - ismétlés

>

> a sokaság minden elemét nem tudjuk megfigyelni technikai okokból ezért a mintából hogyan tudunk következtetni a teljes egészre.

>

> ***bármit is csinálunk akkor se fogunk tudni biztosat mondani a sokaságról***, de elég pontosat nem tudunk mondani soha, és amit mondunk minidg függ amintától

>

> hiába adott rögzített változó a sokaság mértéke és hiába is rögzített a mintavétel mégis mintáról mintára  változni fog, hogy mit adhatunk be

> 

> a becslő függvény tulajdonságaitól szintén függ az eredményünk

>

> - a nagyobb *szórás* kisebb *hatásosság*ot eredményez	



***ha torzítatlan egy becslő akkkor az véges mintás, minden véges mintára működik***



- a minta változtatásával reménykedhetünk abban, hogy minden szélsőértékhez ellentétes sézlsőérték is tartozik majd.

- a mintavételi szórás eloszlása a standard hiba

- a kérdés hogyan függ a stanrd hiba a nagyságtól



$$\lambda_{1}, \lambda_{2},..., \lambda_{n}  - \mathit{N}(\mu , \sigma^{2})$$



$$[\bar{X} = \frac{1}{n} \sum_{i=1}^{n}X_{i}$$



$$D^{2}(\bar{x}) = D^{2}(\frac{1}{n} \sum_{i=1}^{n}X_{i}) = \frac{1}{n^2} D^2 \sum_{i=1}^{n}X_{i} = \frac{1}{n^2} \sum_{i=1}^{n}D^2X_{i} = \frac{\sigma_0^2}{n} \blacksquare$$



$\bar{X}$ mintavételi alak eloszlása = $\mathit{N}(\mu,\sigma^{2})$

Ez a nagymintás tulajdonság.

Ha egy becslő függvény torzított de a torzítás mértéke 0-ba tart akkor a függvény aszimptotikusan torzítatlan. 



A konzisztencia szerint ha végtelemben vagyunk akkor megszűnik az induktív statisztika problémája



csak akkor mondom  konzisztensnek, ha a határértéke 0 



nem is segít a mediánon ha növeljük a mintanagyságot

[centrális határ eloszlás tétel](https://hu.wikipedia.org/wiki/Centr%C3%A1lis_hat%C3%A1reloszl%C3%A1s-t%C3%A9tel)

asziptotikus határ eloszlás ha lognormális a háttér akkor véges mintán nem jó eredményt ad 



## Cramer-Rao tétel

mi az elvi minimuma egy adott szituációban egy becslő mintavételi szórásának



*James Stein-becslő*



Van olyan szituáció ahol létezik hatásos becslő, de annak a varianciája is magasabb mint a Cramer-Rao alsó korlátot.



A Cramer-Raoban a Fisher információ az ami a jellemzőt adja.



A mintaátlag felveszi a Cramer-Rao alsó korlátot. Nem létezik olyan becslő ami torzítatlan és kisebb a varianciája mint a mintaátlagnak.



ha a mintából kiszámoljuk ami a sokaság lesz az még torzítatlan se lesz



véges mintán torzított de aszimptotikusan torzítatlan becslő a minta variancia 



a minta variancia várható értéke mindig az `n/(n-1)`szerese lesz a korrigált mintavariancia: $frac{1}{n-1}\sum(X_i-\bar{X})^2$



Az a cél, hogy megmondjuk, hogy mik azok a valódi értékek amire igaz az, hogy ha az lenne a valóság akkor az kénylmesen beszóródhatna abba amit akpunk is:



 $mathit{\bar{X}} = \mu (\mu , \frac{\sigma_0^{2}}{n})$



$$\bar{X}-\mu = \mu(0,  \frac{\sigma_0^{2}}{n}) = \frac{\bar{X}-\mu}{\sqrt{\sigma_0^2/n}} = \mu(0,1)$$



$$\mathbb{P}(-z<\frac{\bar{X}-\mu}{\sqrt{\sigma_0^2/n}} \mathbb{P}(-z_{1-\frac{\alpha}{2}} < \frac{\bar{X}-\mu}{\sqrt{\sigma_0^2/n}}