Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/gabriel-milan/legal_word2vec

A word2vec model that uses brazilian legal vocabulary as input data, focusing on uses for legaltechs.
https://github.com/gabriel-milan/legal_word2vec

Last synced: about 1 month ago
JSON representation

A word2vec model that uses brazilian legal vocabulary as input data, focusing on uses for legaltechs.

Awesome Lists containing this project

README 

        
# Legal_Word2Vec



  



## Objective



A model that uses brazilian legal vocabulary (with general vocabulary included) in order to generate representative vectors of all words in the dictionary. Since it's done, it can be used to generate representative vectors of general sentences through a very simple weighted average.



  



## Background



### Word2Vec



First of all, we build a simple square matrix *A* or order *n*, in which *n* is the number of words my vocabulary contains. Each *k*-th line of the matrix *A* relates to the *k*-th word of our vocabulary.



This way, we walk through the all the sentences, checking mutual occurencies of a *k*-th word AND a *j*-th word. Once found, we increment the values of ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/001.png) and ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/002.png).



So, at the end of this step, we would have the matrix *A*, in a certain way, correlating words according to their common uses. And how can we extract representative vectors for each word based on *A*?



Back from linear algebra, we have *dot product*, which, according to Wikipedia:

>Algebraically, the dot product is the sum of the [products](https://en.wikipedia.org/wiki/Product_(mathematics) "Product (mathematics)") of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the [Euclidean magnitudes](https://en.wikipedia.org/wiki/Euclidean_vector#Length "Euclidean vector") of the two vectors and the [cosine](https://en.wikipedia.org/wiki/Cosine "Cosine") of the angle between them.



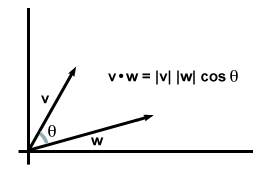
![](http://img.sparknotes.com/figures/1/13493b46f82b15be90229290a86eb26a/dotproduct.gif)



In other words, if we compute the dot product between two  normalized representative vectors (which I will now call *word vectors*) we would have the cosine of the angle between them what, in some way, could tell us more about the similarity of the words.



Now that we assumed that the dot product between two word vectors represent similarity between them, we need ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/003.png) so that ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/004.png), where:

- *W* is the matrix where each column represents a word vector

- *w* is a word vector

- *a* is an element of matrix *A*

- *m* is an arbitrary dimension of the word vectors



Since *A* is square and real symmetric, we can eigendecompose *A* as ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/b05201393504fcd276f510aeac9dbd079b817189) . This way, if I define ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/005.png), ![](https://github.com/gabriel-milan/Legal_Word2Vec/blob/master/readme_img/006.png).



Works like a charm, right? Not actually. This way, *w* would be of order *n*, not *m*. But, considering that the eigenvalues diagonal matrix is sorted for its absolute values, we could truncate it to reduce *w* dimension not wasting much information.



#### But does this work? 

I am still validating this model, so, as told in LICENSE file, I'm not responsible for liability.



### Sentence2Vec

In progress...