Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/gabriel-milan/robotic-sailboat
This repository aims to share knowledge about robotic sailboats, since it's a subject of my personal interest. The content here has been developed by me and, as I'm an Electronic and Computer Engineering student, some of it may have mistakes, please keep aware and warn me about something messed up.
https://github.com/gabriel-milan/robotic-sailboat
Last synced: about 1 month ago
JSON representation
This repository aims to share knowledge about robotic sailboats, since it's a subject of my personal interest. The content here has been developed by me and, as I'm an Electronic and Computer Engineering student, some of it may have mistakes, please keep aware and warn me about something messed up.
- Host: GitHub
- URL: https://github.com/gabriel-milan/robotic-sailboat
- Owner: gabriel-milan
- License: gpl-3.0
- Created: 2018-09-25T00:57:03.000Z (about 6 years ago)
- Default Branch: master
- Last Pushed: 2021-03-14T11:09:43.000Z (over 3 years ago)
- Last Synced: 2024-05-01T17:40:16.240Z (7 months ago)
- Size: 146 KB
- Stars: 2
- Watchers: 1
- Forks: 1
- Open Issues: 1
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# Robotic Sailboat - Wingsail Control
This repository aims to share knowledge about robotic sailboats, since it's a subject of my personal interest. The content here has been developed by me and, as I'm an Electronic and Computer Engineering student, some of it may have mistakes, please keep aware and warn me about something messed up.
## Introduction
In 2017, Minerva Náutica (https://www.facebook.com/minervanautica/), a brazilian team from the Federal University of Rio de Janeiro that develops RC and robotic vessels joined the International Robotic Sailing Competition (https://www.sailbot.org/) for the first time, on its 11th edition, as the first team on the whole southern hemisphere that participated in a competition of that category.
At the time, we were very excited about our results on the competition, getting 5th place in general score and 1st place in the presentation of the project, tied with WPI, a huge team that got 1st place in general score in 2017 and 2018 (information updated on September, 2018).
This is a theoretical, very simple and low cost algorithm very similar to the one used by Minerva Náutica on 2017 that tries to increase boat performance by controlling the wingsail.
## Considerations
For the algorithm you'll see here, there are a few considerations made, as this was my conditions at the time:
* You have a single rigid wingsail;
* You know all the lift/drag coefficients for your single wingsail;
* You have no worries about heeling forces generated by aerodynamics.
## Background
As said on [Wikipedia](https://en.wikipedia.org/wiki/Forces_on_sails),
>**Forces on sails** result from movement of air that interacts with sails and gives them motive power for sailing craft.
There are two forces that results from movement of the air on an airfoil, called Lift and Drag forces, one that's orthogonal to the surface of the airfoil and to the wind (Lift) and the other on the same direction of the apparent wind (a concept as shown on Picture 1 below). These forces are represented on Picture 2.
Picture 1 - Apparent wind

Picture 2 - Airfoil streamlines

And there is a mathematical model which is applied to the design of sails we'll be using for this algorithm that is
where  is the coefficient for the force, that could be
is the coefficient for the force, that could be  for drag force and
for drag force and  for lift force, both of them depending on
for lift force, both of them depending on 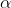 , which is the angle of attack (or the angle between the apparent wind and the sail).
, which is the angle of attack (or the angle between the apparent wind and the sail).
Working on the forces on sail, we can see that there's a force that "pushes" the vessel forward, called the Driving force(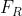 ), indicated below on Picture 3, as Lift Force (
), indicated below on Picture 3, as Lift Force (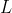 ) and Drag Force (
) and Drag Force (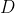 ):
):
Picture 3 - Forces on sail

In order to compute the driving force, we have:
what gives us:
Considering we aren't able to increase 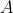 , the area of the sail, and since we can't change
, the area of the sail, and since we can't change 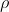 , which is the density of the air, we can assume them as constants so, in order to increase
, which is the density of the air, we can assume them as constants so, in order to increase 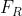 we need to increase either
we need to increase either 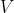 , the speed of the apparent wind, or maximize
, the speed of the apparent wind, or maximize &space;-&space;C_{D}&space;\cdot&space;cos(\alpha)) , which from now on I'll call
, which from now on I'll call  , or *"driving force coefficient"*, so
, or *"driving force coefficient"*, so
And since 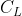 and
and 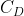 depends only on
depends only on 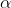 , we can rewrite the equation:
, we can rewrite the equation:
## Example - NACA 0015
In order to explain how it was done back in 2017 as accurately as possible, I'll take the NACA 0015 airfoil for this example. The only auxiliary code I used here is on `examples/`.
### What does NACA 0015 stands for?
>"The **NACA airfoils** are airfoil shapes for aircraft wings developed by the National Advisory Committee for Aeronautics (NACA)." -- Wikipedia
This one, particularly, is a symmetrical 4-digit airfoil and the *"15"* in *0015* indicates the airfoil has a 15% thickness to chord length ratio or, in other words, it is 15% as thick as it is long.
Basically, this is what it looks like:
Picture 4 - NACA 0015 airfoil
### NACA 0015 coefficients
Back in 2017, I got these coefficients from a free software called [Javafoil](https://www.mh-aerotools.de/airfoils/javafoil.htm). For this example I'll get data from the same website I got the picture above, [AirfoilTools.com](http://airfoiltools.com), using the Reynolds number approximately 200 (for information on Reynolds number, please check [this](https://en.wikipedia.org/wiki/Reynolds_number)).
So now we're going to plot 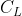 ,
, 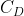 and
and  against
against 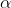 to see what we're dealing with:
to see what we're dealing with:
Picture 5 - Lift coefficient vs Alpha

Picture 6 - Drag coefficient vs Alpha

Picture 7 - Driving coefficient vs Alpha

It is pretty intuitive that 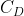 and
and 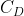 are mirrored on
are mirrored on  and
and  , and
, and 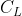 on
on  equals
equals  on
on  , being
, being 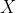 the horizontal axis on the charts. This said, from now on we'll only use the
the horizontal axis on the charts. This said, from now on we'll only use the  side of them.
side of them.
### The stall issue
As we can see on the *"Lift coefficient vs Alpha"* chart, next to 14 degrees, it has its greatest value and then starts decreasing very fast. This phenomenon is called *stall*, and it's defined by:
>"A stall is a condition in aerodynamics and aviation wherein the angle of attack increases beyond a certain point such that lift begins to decrease. The angle at which this occurs is called the *critical angle of attack*.
>[...]
>[Flow separation](https://en.wikipedia.org/wiki/Flow_separation) begins to occur at small angles of attack while attached flow over the wing is still dominant. As angle of attack increases, the separated regions on the top of the wing increase in size and hinder the wing's ability to create lift. At the critical angle of attack, separated flow is so dominant that additional incr\alphaeases in angle of attack produce less lift and more drag." -- Wikipedia
In other words, it may be risky to choose an *"ideal"* 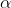 greater than the *critical angle* (
greater than the *critical angle* ( , from now on), even though its
, from now on), even though its  may be greater than
may be greater than  's.
's.
### Choosing Alpha
Okay, now that we know how to do it, let's just do it!
On the auxiliary code I uploaded, there's a function `max_value (data, x_label, y_label)` that returns the greatest 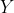 value in the dataset for the given
value in the dataset for the given 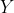 versus
versus 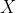 chart and its respective
chart and its respective 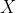 value. This considered, the output we get for
value. This considered, the output we get for  and
and  , respectively, is the following:
, respectively, is the following:
`(14.25, 1.2139)`
`(14.5, 0.254183875029455)`
This is pretty clear if we plot both 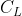 (in red) and
(in red) and  (in green), as follows:
(in green), as follows:
Picture 8 - Lift and Driving coefficients vs Alpha

Being aware of the *stall* issue, we shall consider taking our  instead of
instead of  and, as curious as I am, I got to check the difference it will bring me, so I'll check the value of
and, as curious as I am, I got to check the difference it will bring me, so I'll check the value of  for
for  too.
too.
In this particular example,  for
for  , which will give me
, which will give me
}{C_R(14.5)}&space;=&space;\frac{0.253639}{0.254183}&space;=&space;99,8\%) of the best performance according to this model.
of the best performance according to this model.
This is a risk I, personally, wouldn't take, considering the tiny difference on performance. So, for this example, we'll be assuming
as our final answer.
----------
> ---> TODO:
>* Simple example Arduino code to control sail
>* Final considerations