https://github.com/gagniuc/markov-chains-prediction-framework

This application makes predictions by multiplying a probability vector with a transition matrix multiple times (n steps - user defined). On each step the values from the resulting probability vectors are plotted on a chart. The resulting curves on the chart indicate the behavior of the system over a number of steps.
https://github.com/gagniuc/markov-chains-prediction-framework

markov-chains markov-model prediction probability transition transition-matrix vb6 vectors

Last synced: 7 months ago
JSON representation

This application makes predictions by multiplying a probability vector with a transition matrix multiple times (n steps - user defined). On each step the values from the resulting probability vectors are plotted on a chart. The resulting curves on the chart indicate the behavior of the system over a number of steps.

• Host: GitHub
• URL: https://github.com/gagniuc/markov-chains-prediction-framework
• Owner: Gagniuc
• License: mit
• Created: 2021-10-28T21:55:33.000Z (almost 4 years ago)
• Default Branch: main
• Last Pushed: 2022-11-17T07:09:10.000Z (almost 3 years ago)
• Last Synced: 2025-01-15T07:31:56.522Z (9 months ago)
• Topics: markov-chains, markov-model, prediction, probability, transition, transition-matrix, vb6, vectors
• Language: Visual Basic 6.0
• Homepage:
• Size: 64.5 KB
• Stars: 5
• Watchers: 1
• Forks: 2
• Open Issues: 0
• Metadata Files:
  • Readme: README.md
  • Funding: .github/FUNDING.yml
  • License: LICENSE.md

Awesome Lists containing this project

README

          
# Markov Chains Prediction framework

The application multiplies a probability vector with a transition matrix multiple times (n steps - user defined). On each step, the values from the resulting probability vectors are plotted on a chart. The resulting curves on the chart indicate the behavior of the system over n steps. Note that the application allows a prediction for systems with a maximum of four states. [This version in JS](https://gagniuc.github.io/Predictions-with-Markov-Chains/) can also be of use: [Predictions with Markov Chains](https://github.com/Gagniuc/Predictions-with-Markov-Chains).

![screenshot](https://github.com/Gagniuc/Markov-Chains-Prediction-framework/blob/main/img/Markov%20Chains%20-%20Prediction%20framework.png?raw=true)

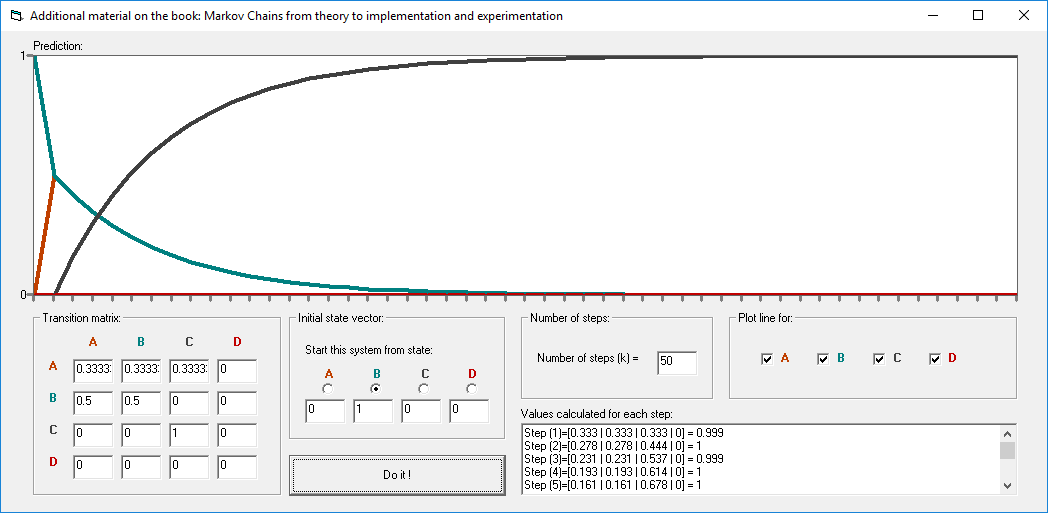
![screenshot](https://github.com/Gagniuc/Markov-Chains-Prediction-framework/blob/main/img/Markov%20Chains%20-%20Prediction%20framework%20(new%20setup).png?raw=true)

# References

- Paul A. Gagniuc. Markov chains: from theory to implementation and experimentation. Hoboken, NJ,  John Wiley & Sons, USA, 2017, ISBN: 978-1-119-38755-8.