https://github.com/garrettj403/czt

Chirp Z-Transform
https://github.com/garrettj403/czt

czt dft dsp fourier-transform frequency-domain signal-processing z-transform

Last synced: 10 months ago
JSON representation

Chirp Z-Transform

• Host: GitHub
• URL: https://github.com/garrettj403/czt
• Owner: garrettj403
• License: mit
• Created: 2020-11-25T15:22:31.000Z (about 5 years ago)
• Default Branch: main
• Last Pushed: 2024-12-20T07:34:08.000Z (about 1 year ago)
• Last Synced: 2025-03-30T11:06:37.980Z (11 months ago)
• Topics: czt, dft, dsp, fourier-transform, frequency-domain, signal-processing, z-transform
• Language: Python
• Homepage:
• Size: 12.2 MB
• Stars: 44
• Watchers: 4
• Forks: 16
• Open Issues: 0
• Metadata Files:
  • Readme: README.md
  • Changelog: CHANGES.md
  • License: LICENSE

Awesome Lists containing this project

README

          
Chirp Z-Transform (CZT)

=======================

[![PyPI version](https://badge.fury.io/py/czt.svg)](https://badge.fury.io/py/czt)

[![ci](https://github.com/garrettj403/CZT/actions/workflows/ci.yml/badge.svg)](https://github.com/garrettj403/CZT/actions/workflows/ci.yml)

[![flake8](https://github.com/garrettj403/CZT/actions/workflows/linter.yml/badge.svg)](https://github.com/garrettj403/CZT/actions/workflows/linter.yml)

From [Wikipedia](https://en.wikipedia.org/wiki/Chirp_Z-transform):

> The chirp Z-transform (CZT) is a generalization of the discrete Fourier transform (DFT). While the DFT samples the Z plane at uniformly-spaced points along the unit circle, the chirp Z-transform samples along spiral arcs in the Z-plane, corresponding to straight lines in the S plane. The DFT, real DFT, and zoom DFT can be calculated as special cases of the CZT.

Getting Started

---------------

You can install the CZT package using ``pip``:

   ```bash

   # to install the latest release (from PyPI)

   pip install czt

   # to install the latest commit (from GitHub)

   git clone https://github.com/garrettj403/CZT.git

   cd CZT

   pip install -e .

   # to install dependencies for examples

   pip install -e .[examples]

   

   # to install dependencies for testing

   pip install -e .[testing]

   ```

Example

-------

Consider the following time-domain signal:







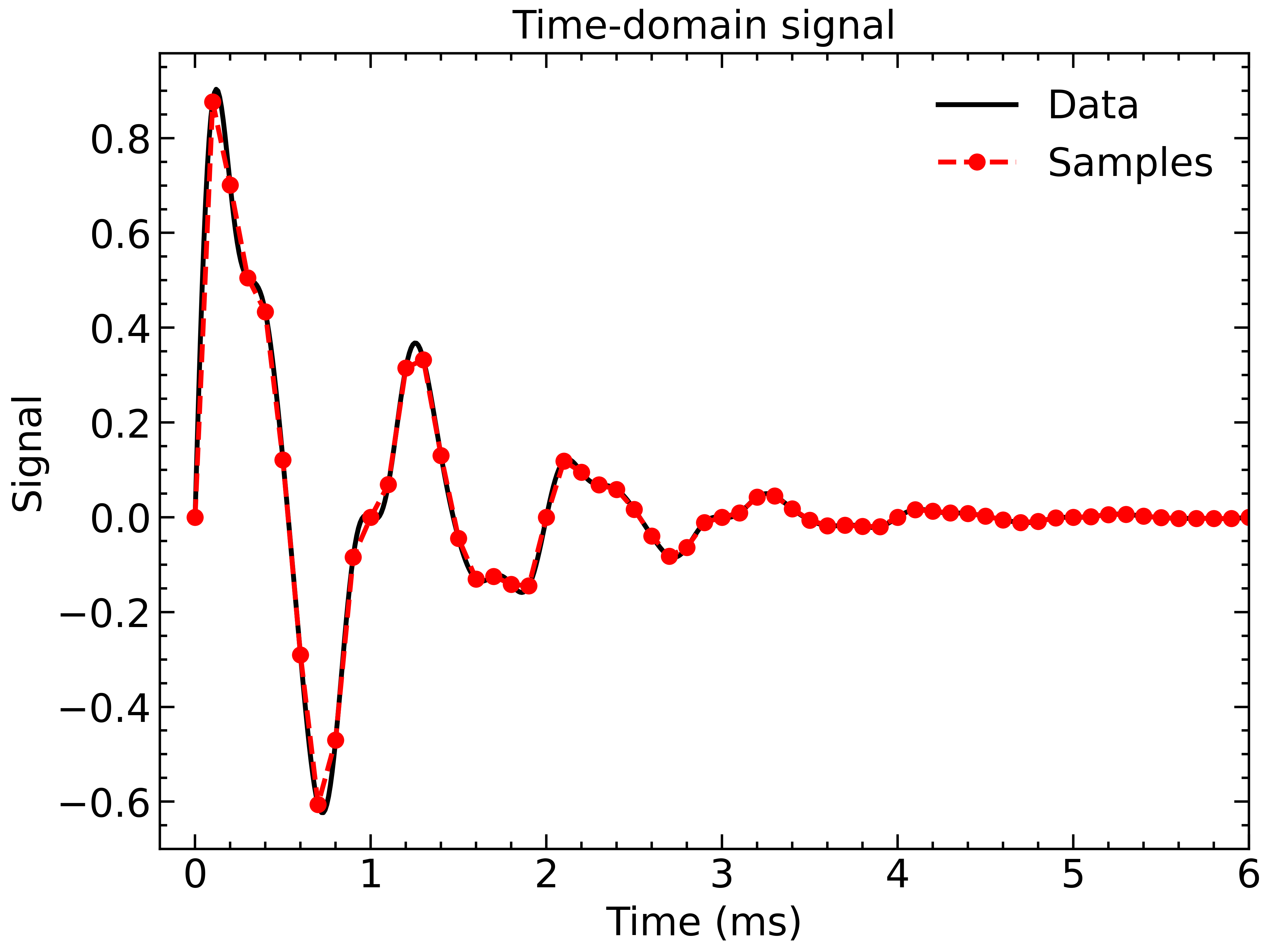
This is an exponentially decaying sine wave with some distortion from higher-order frequencies. We can convert this signal to the frequency-domain to investigate the frequency content using the Chirp Z-Transform (CZT):







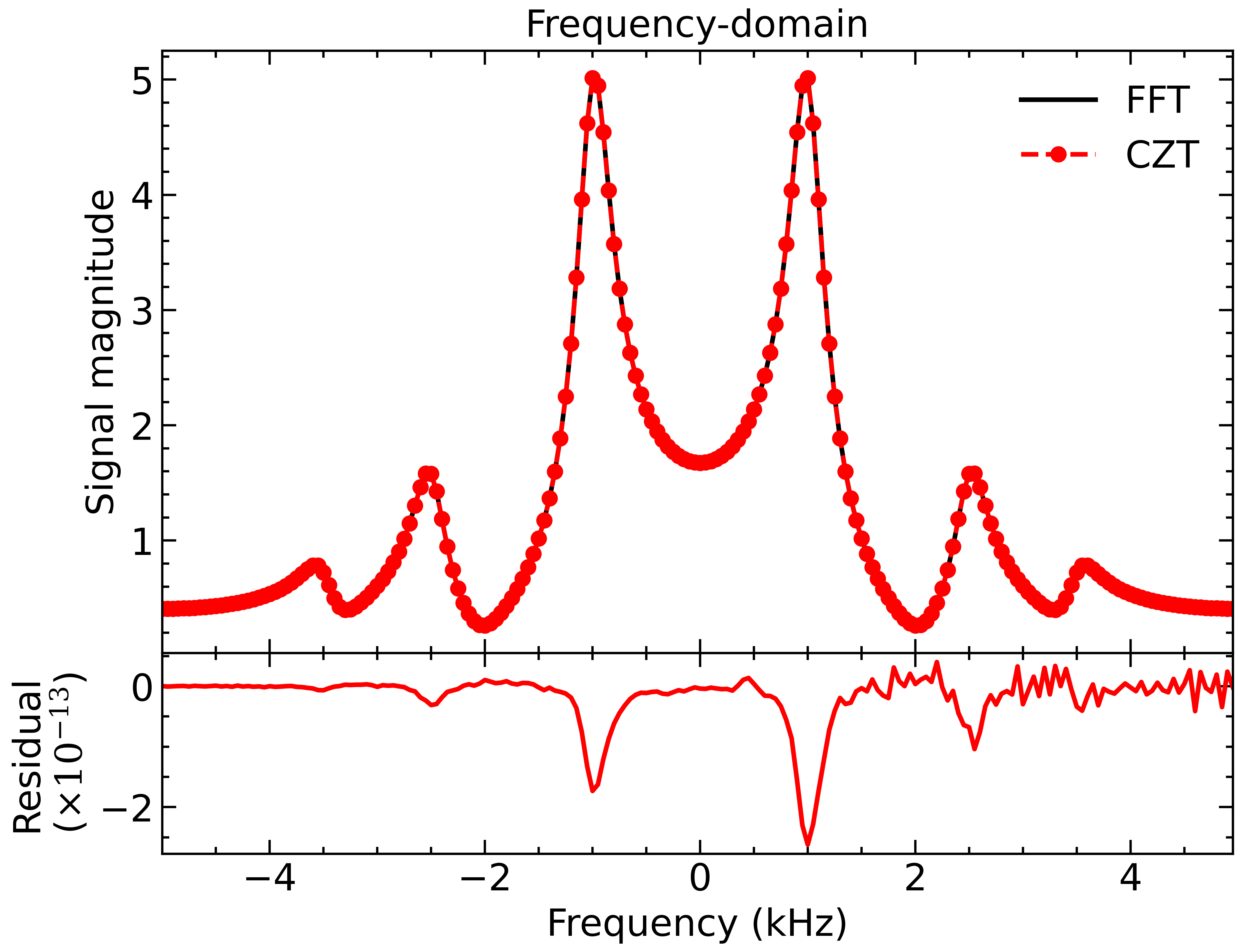
Note that the CZT also allows us to calculate the frequency response over an arbitrary frequency range:







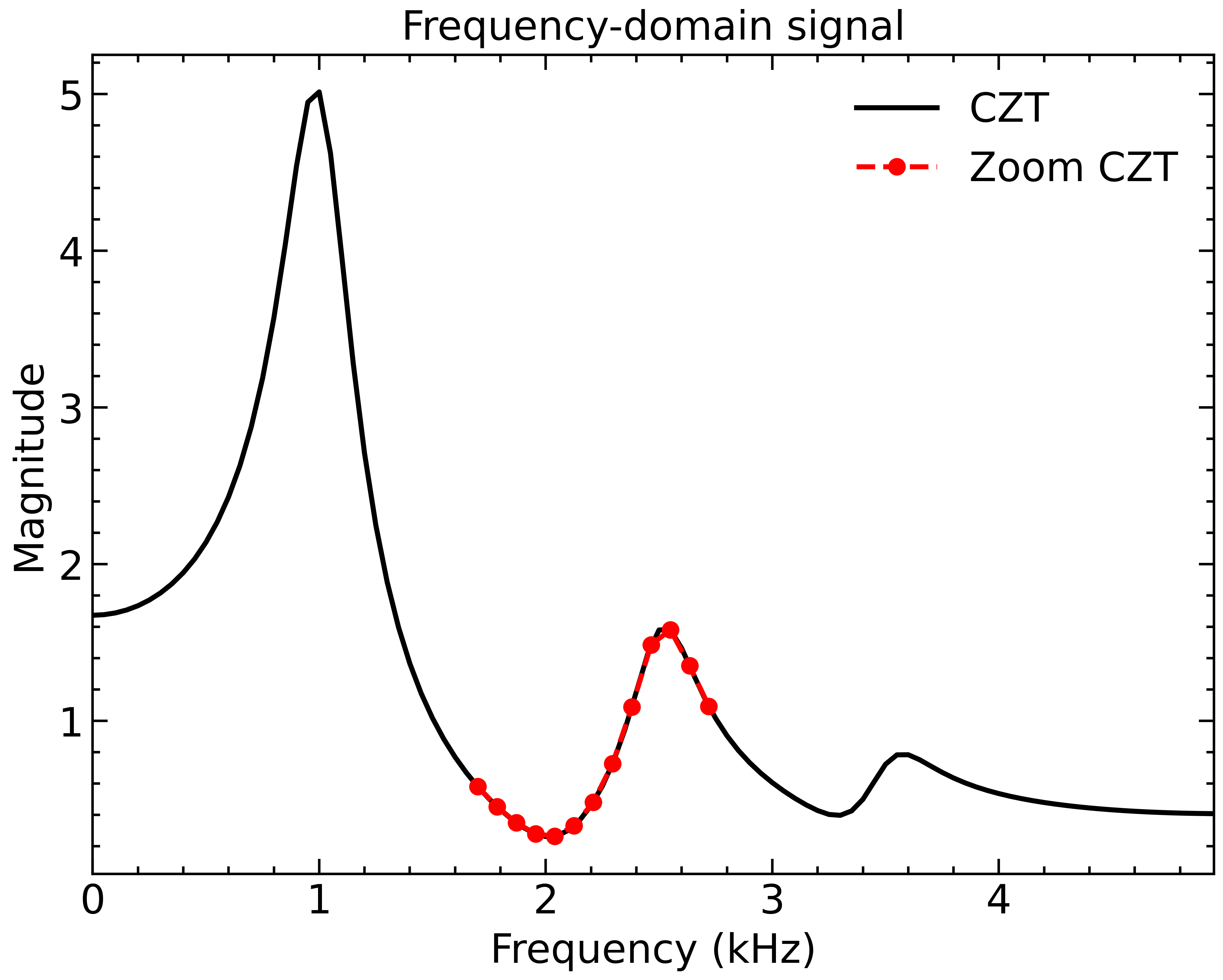
We can see that the signal has frequency components at 1 kHz, 2.5 kHz and 3.5 kHz. To remove the distortion and isolate the 1 kHz signal, we can apply a simple window in the frequency-domain:







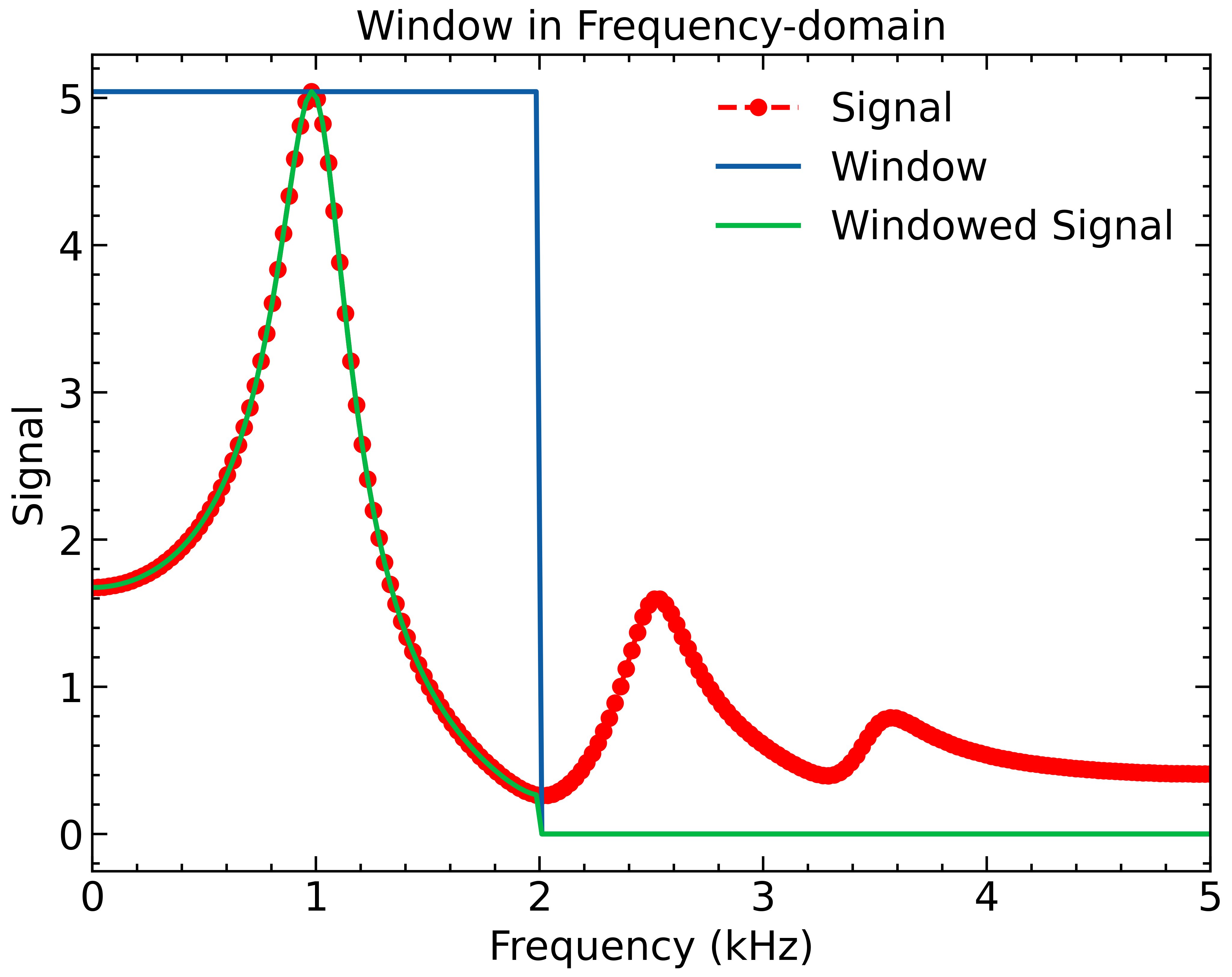
Finally, we can use the Inverse Chirp Z-Transform (ICZT) to transform back to the time domain:







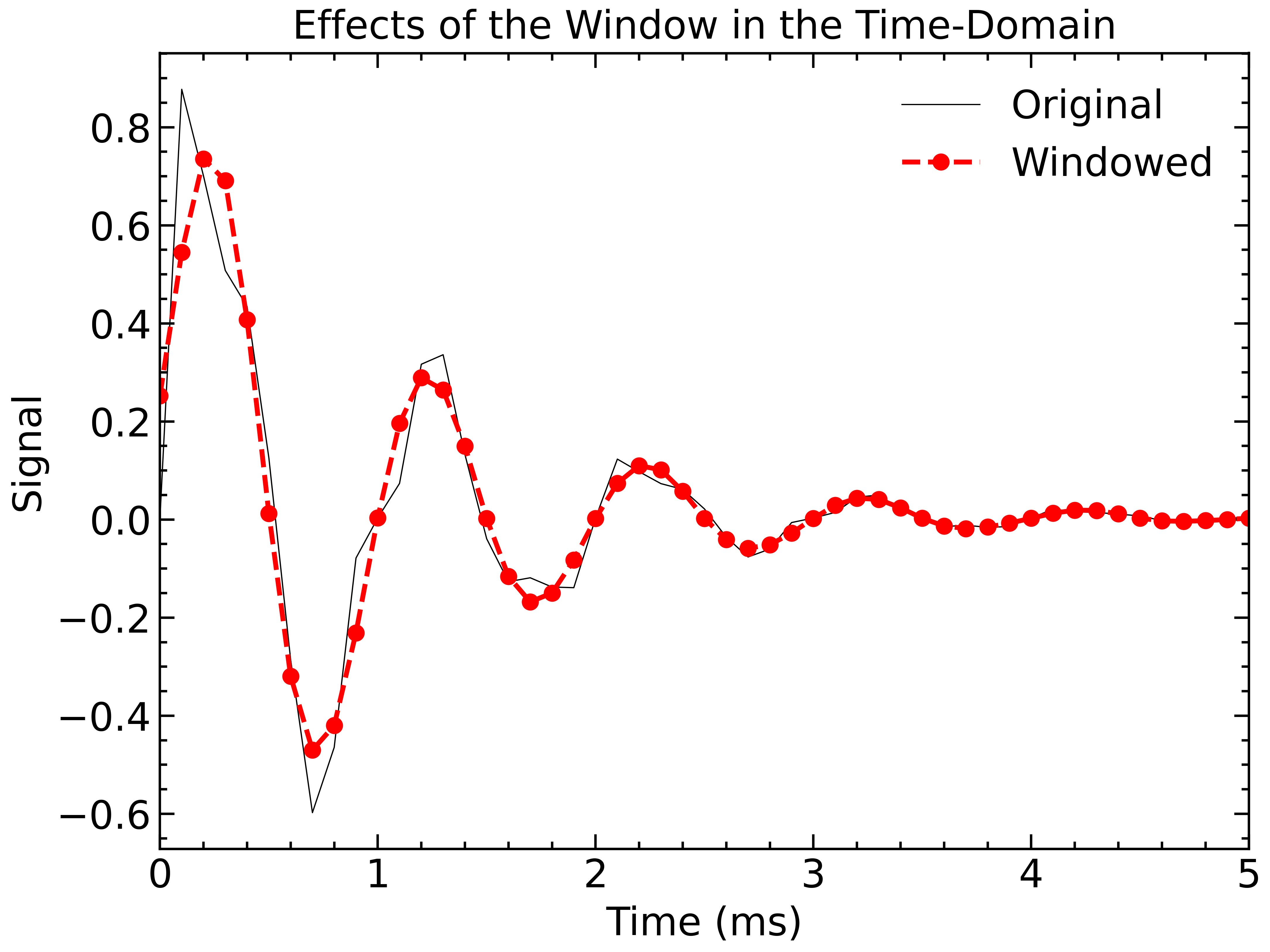
As we can see, we were able to remove the higher-order frequencies that were distorting our 1 kHz signal.

You can find this example and others in the [``examples/``](https://github.com/garrettj403/CZT/blob/main/examples/)  directory.

References

----------

- [L. Rabiner, R. Schafer and C. Rader, "The chirp z-transform algorithm," *IEEE Transactions on Audio and Electroacoustics*, vol. 17, no. 2, pp. 86-92, Jun. 1969, doi: 10.1109/TAU.1969.1162034.](https://web.ece.ucsb.edu/Faculty/Rabiner/ece259/Reprints/015_czt.pdf)

- [V. Sukhoy and A. Stoytchev, "Generalizing the inverse FFT off the unit circle," *Scientific Reports*, vol. 9, no. 14443, Oct. 2019, doi: 10.1038/s41598-019-50234-9.](https://doi.org/10.1038/s41598-019-50234-9)

- [Chirp Z-Transform (Wikipedia)](https://en.wikipedia.org/wiki/Chirp_Z-transform)

- [Discrete Fourier Transform (Wikipedia)](https://en.wikipedia.org/wiki/Discrete_Fourier_transform)