https://github.com/geekquad/lasso-ridge-regression-and-elastic_net-regularization-from-scratch
Basic implementation of Lasso, Ridge Regression and Elastic-Net Regularization.
https://github.com/geekquad/lasso-ridge-regression-and-elastic_net-regularization-from-scratch
boston-housing-dataset elasticnetregression feature-selection lasso-regression regression regression-analysis regularization ridge-regression sklearn
Last synced: 8 months ago
JSON representation
Basic implementation of Lasso, Ridge Regression and Elastic-Net Regularization.
- Host: GitHub
- URL: https://github.com/geekquad/lasso-ridge-regression-and-elastic_net-regularization-from-scratch
- Owner: geekquad
- Created: 2020-07-11T22:12:27.000Z (about 5 years ago)
- Default Branch: master
- Last Pushed: 2020-07-12T13:24:41.000Z (about 5 years ago)
- Last Synced: 2025-01-07T05:16:47.020Z (9 months ago)
- Topics: boston-housing-dataset, elasticnetregression, feature-selection, lasso-regression, regression, regression-analysis, regularization, ridge-regression, sklearn
- Language: Jupyter Notebook
- Homepage:
- Size: 624 KB
- Stars: 2
- Watchers: 1
- Forks: 1
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Lasso-Ridge-Regression-and-Elastic_Net-Regularization-from-Scratch
## Feature Selection:
We want to have a minimal number of eatures that it takes to really capture the trends and patterns of our data.
```
*NOTE:
Features != Information
```
Why do we do Feature Selection?
- It enables the machine learning algorithm to train faster.
- It reduces the complexity of a model and makes it easier to interpret.
- It improves the accuracy of a model if the right subset is chosen.
## Regularization:
- This is the method for automatically penalizing extra features.
- It can set the coefficient of a feature to zero.
**There are some pre-defined modules/libraries in sklearn that helps us in Reglarization/Feature Selection.**
1. Lasso Regression
2. Ridge Regression
3. Elasric-Net Regularization
## Lasso Regression:
- In Lasso Regression, we add Mean Absolute Value of coefficients.
- Lasso regression can completely eliminate the variable by reducing its coefficient value to 0.
- The new term we added to Ordinary Least Square(OLS) is called L1 Regularization.
##### **Formula:**
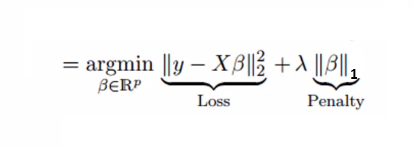
The second term is basically a paramter with the term that describes how many features we are using.
##### **Plotting Lasso Regression's Coefficient Score:**

##### **Documentation of LASSO:**
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
## Ridge Regression:
- In Ridge Regression, we add Mean Square Values of coefficients.
- This term is the sum of squares of coefficient multiplied by the parameter.
- The motive of adding this term is to penalize the variable corresponding to that coefficient not very much correlated to the target variable.
##### **Formula:**
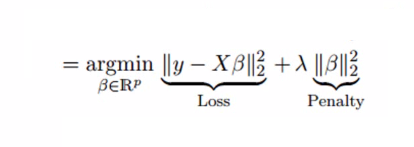
In this equation, we have two components. First one is least square term and other one is lambda of the summation of β2 (beta- square) where β is the coefficient. This is added to least square term in order to shrink the parameter to have a very low variance.
##### **Plotting Ridge Regression's Coefficient Score:**

##### **Documentation of RIDGE:**
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html
## Elastic-Net Regularizatoin:
- ElasticNet is hybrid of Lasso and Ridge Regression techniques.
- It is trained with L1 and L2 prior as regularizer.
- Elastic-net is useful when there are multiple features which are correlated. Lasso is likely to pick one of these at random, while elastic-net is likely to pick both.
##### **Formula:**
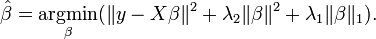
In elastic Net Regularization we added the both terms of L1 and L2 to get the final loss function.
##### **Plotting Elastic-Net Regularization's Coefficient Score:**

##### **Documentation of ELASTIC-NET:**
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html