Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/goessl/hermite-function
A Hermite function series module.
https://github.com/goessl/hermite-function
easy hermite hermite-functions hermite-polynomial hermite-polynomials hilbert lightweight numpy pip pip3 pypi python python3 vector vector-space wavefunction
Last synced: about 2 months ago
JSON representation
A Hermite function series module.
- Host: GitHub
- URL: https://github.com/goessl/hermite-function
- Owner: goessl
- License: mit
- Created: 2022-12-03T20:54:49.000Z (about 2 years ago)
- Default Branch: main
- Last Pushed: 2024-11-07T17:51:07.000Z (3 months ago)
- Last Synced: 2024-11-15T09:51:04.721Z (2 months ago)
- Topics: easy, hermite, hermite-functions, hermite-polynomial, hermite-polynomials, hilbert, lightweight, numpy, pip, pip3, pypi, python, python3, vector, vector-space, wavefunction
- Language: Python
- Homepage:
- Size: 1.33 MB
- Stars: 0
- Watchers: 2
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# Hermite Function Series
A Hermite function series module.
```python
from hermitefunction import HermiteFunction
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, +4, 1000)
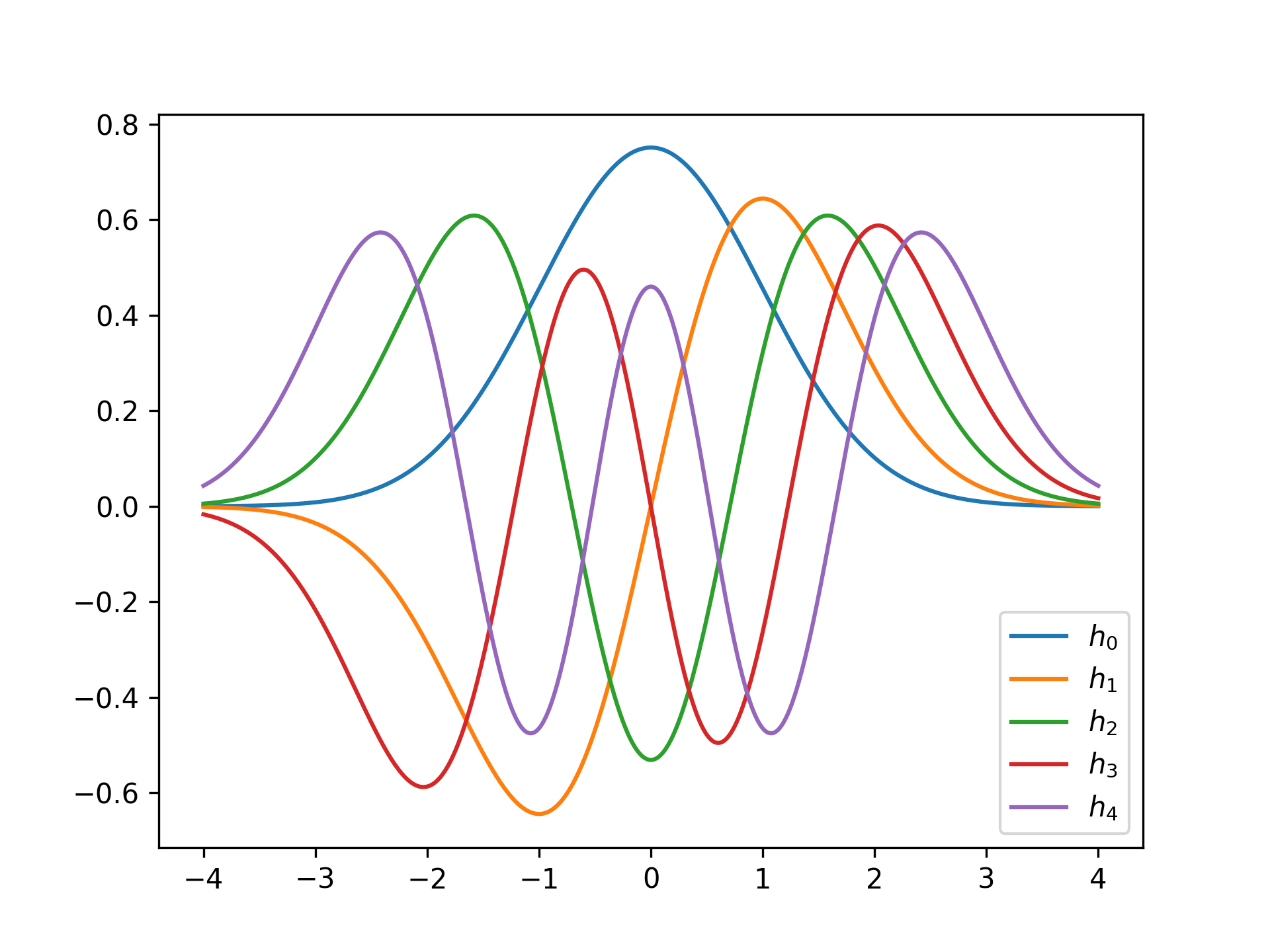
for n in range(5):
f = HermiteFunction(n)
plt.plot(x, f(x), label=f'$h_{n}$')
plt.legend(loc='lower right')
plt.show()
```
## Installation
```
pip install git+https://github.com/goessl/vector.git
pip install hermite-function
```
## Usage
This package provides a single class, `HermiteFunction`, to handle Hermite function series.
`HermiteFunction` extends [`Vector`](https://github.com/goessl/vector/blob/main/vector.py) from the [vector module](https://github.com/goessl/vector) and therefore provides all Hilbert space operations from coefficient access through indexing, over norm calculation to arithmetic.
A series can be initialized in three ways:
- With the constructor `HermiteFunction(coef)`, that takes a non-negative integer to create a pure Hermite function with the given index, or an iterable of coefficients to create a Hermite function series.
- With the random factories `HermiteFunction.rand(deg)` & `HermiteFunction.randn(deg, normed=True)` for a random Hermite function series of a given degree.
- By fitting data with `HermiteFunction.fit(X, y, deg)`.
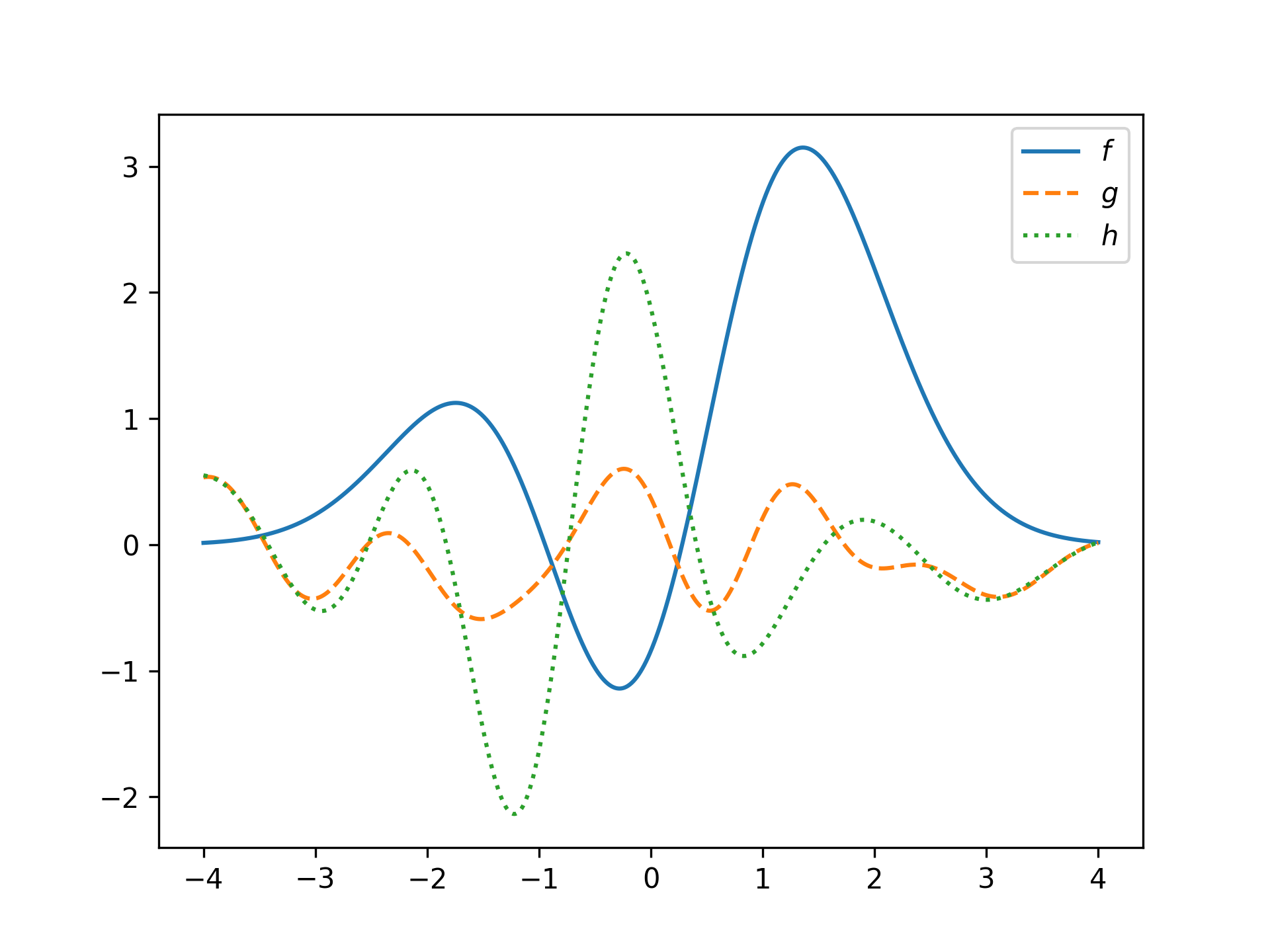
```python
f = HermiteFunction((1, 2, 3))
g = HermiteFunction.randn(15)
h = HermiteFunction.fit(x, g(x), 10)
plt.plot(x, f(x), label='$f$')
plt.plot(x, g(x), '--', label='$g$')
plt.plot(x, h(x), ':', label='$h$')
plt.legend()
plt.show()
```
Methods for functions:
- evaluation with `f(x)`,
- differentiation to an arbitrary degree `f.der(n)`,
- integration `f.antider()`,
- Fourier transformation `f.fourier()` &
- getting the degree of the series `f.deg` are implemented.
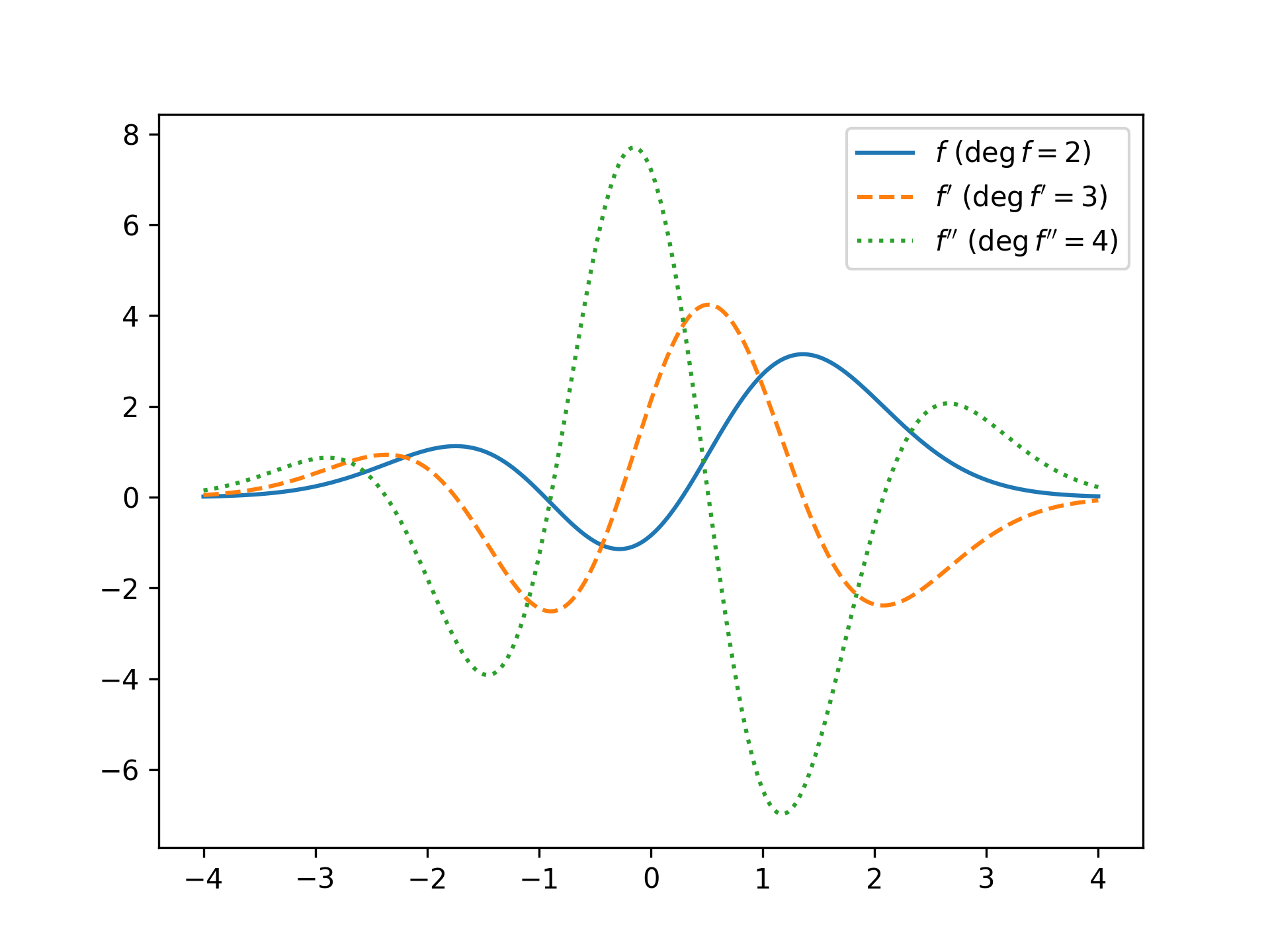
```python
f_p = f.der()
f_pp = f.der(2)
plt.plot(x, f(x), label=rf"$f \ (\deg f={f.deg})$")
plt.plot(x, f_p(x), '--', label=rf"$f' \ (\deg f'={f_p.deg})$")
plt.plot(x, f_pp(x), ':', label=rf"$f'' \ (\deg f''={f_pp.deg})$")
plt.legend()
plt.show()
```
Hilbert space operations inherited from [vector](https://github.com/goessl/vector)
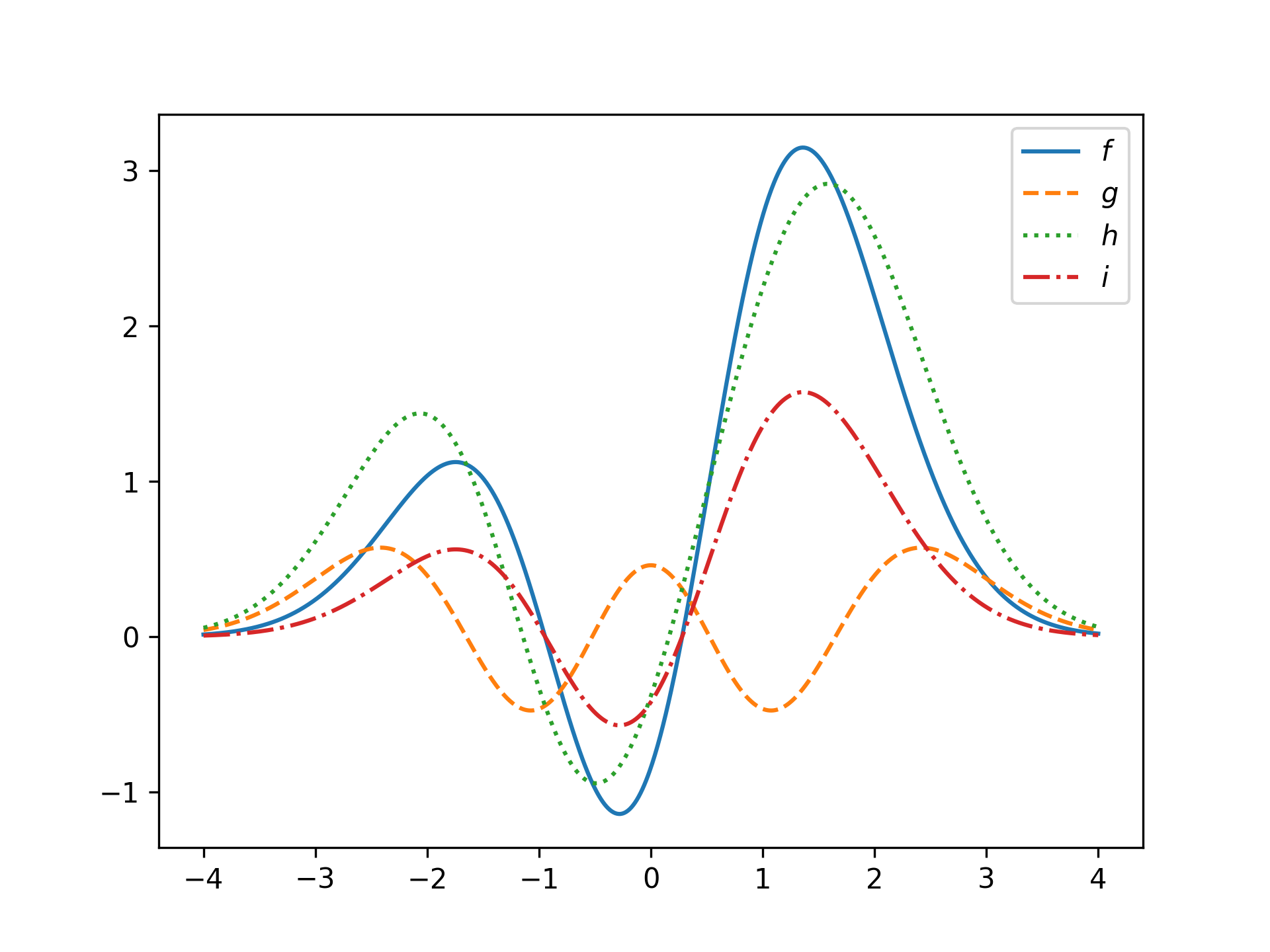
```python
g = HermiteFunction(4)
h = f + g
i = 0.5 * f
plt.plot(x, f(x), label='$f$')
plt.plot(x, g(x), '--', label='$g$')
plt.plot(x, h(x), ':', label='$h$')
plt.plot(x, i(x), '-.', label='$i$')
plt.legend()
plt.show()
```
Because this package was intended as a tool to work with quantum mechanical wavefunctions, the expectation value for the kinetic energy is also implemented ($\langle\hat{P}^2\rangle=\frac{1}{2}\int_\mathbb{R}f^*(x)f''(x)dx$, natural units):
```python
f.kin
```
## Proofs
In the following let
$$
f=\sum_{k=0}^\infty f_k h_k, \ g=\sum_{k=0}^\infty g_k h_k.
$$
where $h_k$ are the Hermite functions, defined by the Hermite polynomials $H_k$:
$$
h_k(x) = \frac{e^{-\frac{x^2}{2}}}{\sqrt{2^kk!\sqrt{\pi}}} H_k(x)
$$
from [Wikipedia - Hermite functions](https://en.wikipedia.org/wiki/Hermite_polynomials\#Hermite_functions).
### Differentiation
$$
\begin{aligned}
f' &= \sum_k f_k h_k' \\
&\qquad\mid h'\_k = \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \\
&= \sum_k f_k \left( \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \right) \\
&= \sum_{k=0}^\infty f_k\sqrt{\frac{k}{2}} h_{k-1} - \sum_{k=0}^\infty f_k\sqrt{\frac{k+1}{2}} h_{k+1} \\
&\qquad\mid k-1 \to k, \ k+1 \to k \\
&= \sum_{k=-1}^\infty \sqrt{\frac{k+1}{2}}f_{k+1} h_k - \sum_{k=1}^\infty \sqrt{\frac{k}{2}}f_{k-1} h_k \\
&\qquad\mid -0+0 = -\sqrt{\frac{-1+1}{2}}f_{-1+1}h_{-1} + \sqrt{\frac{0}{2}}f_{0-1} h_0 \\
&= \sum_{k=0}^\infty \sqrt{\frac{k+1}{2}}f_{k+1} h_k - \sum_{k=0}^\infty \sqrt{\frac{k}{2}}f_{k-1} h_k \\
&= \sum_k \left( \sqrt{\frac{k+1}{2}}f_{k+1} - \sqrt{\frac{k}{2}}f_{k-1} \right) h_k
\end{aligned}
$$
With $h'\_k=\sqrt{\frac{k}{2}}h_{k+1}-\sqrt{\frac{k+1}{2}}h_{k-1}$ from [Wikipedia - Hermite functions](https://en.wikipedia.org/wiki/Hermite_polynomials\#Hermite_functions).
### Integration
With the same relation as above we get
$$
\begin{aligned}
h_k' &= \sqrt{\frac{k}{2}}h_{k-1} - \sqrt{\frac{k+1}{2}}h_{k+1} \\
&\qquad\mid +\sqrt{\frac{k+1}{2}}h_{k+1} - h_k' \\
\sqrt{\frac{k+1}{2}}h_{k+1} &= \sqrt{\frac{k}{2}}h_{k-1} - h_k' \\
&\qquad\mid \cdot\sqrt{\frac{2}{k+1}} \\
h_{k+1} &= \sqrt{\frac{k}{k+1}}h_{k-1} - \sqrt{\frac{2}{k+1}}h_k' \\
&\qquad\mid k+1 \to k \\
h_k &= \sqrt{\frac{k-1}{k}}h_{k-2} - \sqrt{\frac{2}{k}}h_{k-1}' \\
&\qquad\mid \int \\
H_k &= \sqrt{\frac{k-1}{k}}H_{k-2} - \sqrt{\frac{2}{k}}h_{k-1}
\end{aligned}
$$
which can be applied from the highest to the lowest order. For $h_0$ we then get
$$
H_0(x) = \int_{-\infty}^xh_0(x')dx' = \int_{-\infty}^x\frac{e^{-\frac{x'^2}{2}}}{\sqrt[4]{\pi}}dx' = \sqrt{\frac{\sqrt{\pi}}{2}}\text{erf}\left(\frac{x}{\sqrt{2}}\right) \ \left(+\sqrt{\frac{\sqrt{\pi}}{2}}\right)
$$
### Fourier transformation
[Wikipedia - Hermite functions](https://en.wikipedia.org/wiki/Hermite_polynomials#Hermite_functions_as_eigenfunctions_of_the_Fourier_transform)
### Kinetic energy
$$
\left\langle\frac{-\hat{P}^2}{2}\right\rangle = -\frac{1}{2}\int_{\mathbb{R}}f^*(x)\frac{d^2}{dx^2}f(x)dx = +\frac{1}{2}\int_{\mathbb{R}}|f'(x)|^2dx = \frac{1}{2}||f'||\_{L_{\mathbb{R}}^2}^2
$$
## License (MIT)
Copyright (c) 2022 Sebastian Gössl
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.