https://github.com/iandennismiller/i0
i0 is the zero-targeting module for R that puts you in charge of your intercept.
https://github.com/iandennismiller/i0
Last synced: 6 months ago
JSON representation
i0 is the zero-targeting module for R that puts you in charge of your intercept.
- Host: GitHub
- URL: https://github.com/iandennismiller/i0
- Owner: iandennismiller
- License: mit
- Created: 2013-10-25T21:02:46.000Z (almost 12 years ago)
- Default Branch: master
- Last Pushed: 2013-10-28T17:37:39.000Z (almost 12 years ago)
- Last Synced: 2023-04-18T03:24:45.739Z (over 2 years ago)
- Language: R
- Homepage: http://iandennismiller.github.io/i0/
- Size: 1.29 MB
- Stars: 0
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# i0
**i0** (pronounced "i-zero") provides a simple interface for exploring interactions in linear models. This R package is an implementation of the methods in Page-Gould and Miller (submitted), which extends Aiken and West (1991).
## usage
```R
# load the i0 library
library(i0)
# the following dataset comes with the i0 package
data(candy_example)
# create a zero-targeted model using the dataset
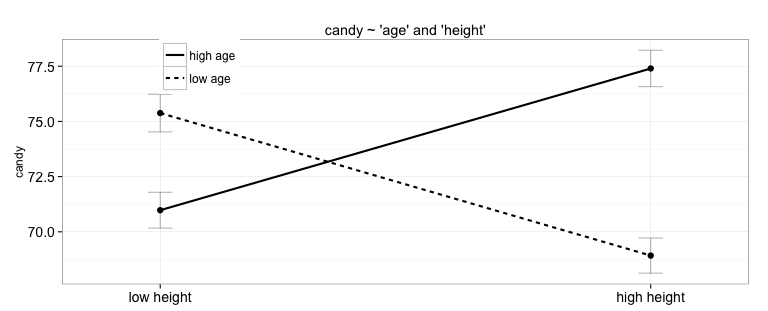
zt = target(candy ~ age + height + age * height, data=candy_example)
# explore +/- 1 standard deviation like Aiken and West (1991)
plot(zt)
```
## installation
The **i0** R package is easily installed using R or RStudio. In the R console, load **devtools** and install **i0** from the project website:
```R
library(devtools)
install_github("i0", "iandennismiller")
```
If you receive the message `Error in library(devtools) : there is no package called devtools`, you must first install **devtools** (see instructions below) then try again.
```R
install.packages("devtools")
```
## documentation
- [Examples](https://github.com/iandennismiller/i0/wiki/Examples)
- [Project Website](http://iandennismiller.github.io/i0)
- [Source Code](https://github.com/iandennismiller/i0)
## support
Please visit the [issue tracker](https://github.com/iandennismiller/i0/issues) on github to report a problem.
## references
Aiken, L. S., & West, S. G. (1991). Multiple regression: Testing and interpreting interactions. Sage Publications, Inc.
Page-Gould, E., & Miller, I. D. (submitted). Zeroing in on the intercept: Estimating marginal means and standard errors with linear models.