https://github.com/innofang/quantify

📐 A desktop application practice and powered by JavaFx. (Curriculum design for algorithm)
https://github.com/innofang/quantify

algorithm algorithm-design curriculum-design curriculum-project javafx javafx-application javafx-desktop-apps quantify quantization

Last synced: about 1 month ago
JSON representation

📐 A desktop application practice and powered by JavaFx. (Curriculum design for algorithm)

• Host: GitHub
• URL: https://github.com/innofang/quantify
• Owner: InnoFang
• License: apache-2.0
• Created: 2017-06-02T13:34:04.000Z (about 8 years ago)
• Default Branch: master
• Last Pushed: 2020-06-26T14:13:35.000Z (almost 5 years ago)
• Last Synced: 2025-04-04T01:11:19.508Z (3 months ago)
• Topics: algorithm, algorithm-design, curriculum-design, curriculum-project, javafx, javafx-application, javafx-desktop-apps, quantify, quantization
• Language: Java
• Homepage:
• Size: 298 KB
• Stars: 4
• Watchers: 1
• Forks: 1
• Open Issues: 0
• Metadata Files:
  • Readme: README.md
  • License: LICENSE

Awesome Lists containing this project

README

        
# Quantify

Algorithm Design

English | [中文](https://github.com/InnoFang/Quantify/blob/master/README_zh.md)

# Description

The quantization process represents a wide range of values ​​as a small range of approximations, thus achieving lossy compression. For example: 16-bit JPG file into a 4-color GIF file, is to RGB color space color quantification into four colors of the process. In addition, four students who are 161,164,178,184 are represented as "one of the 160-169 stages, one in the 170-179 stage and one in the 180th stage" is also quantified.

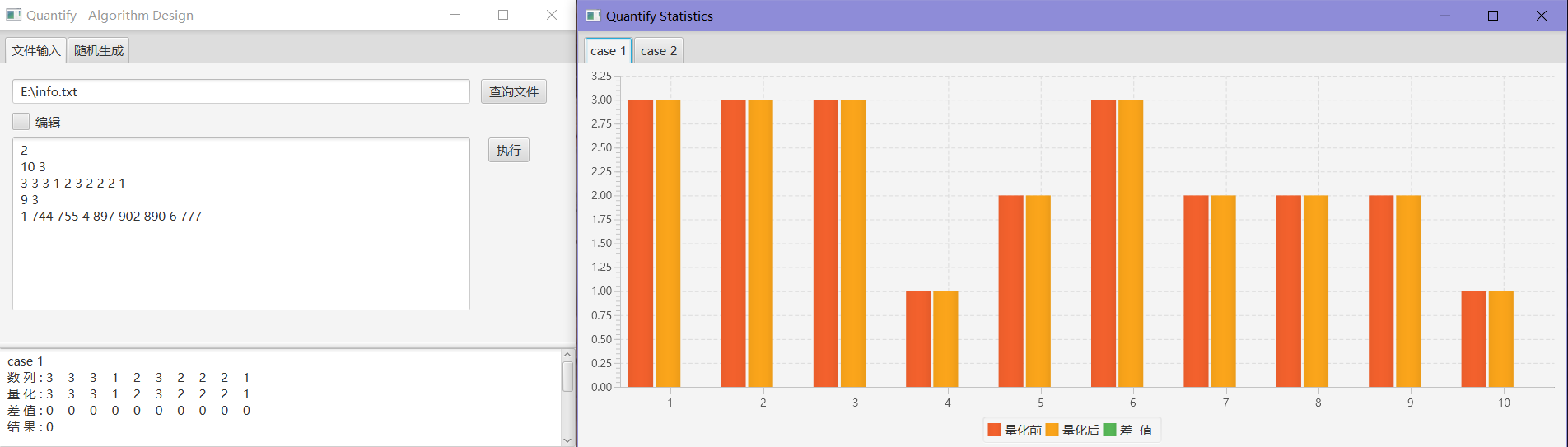
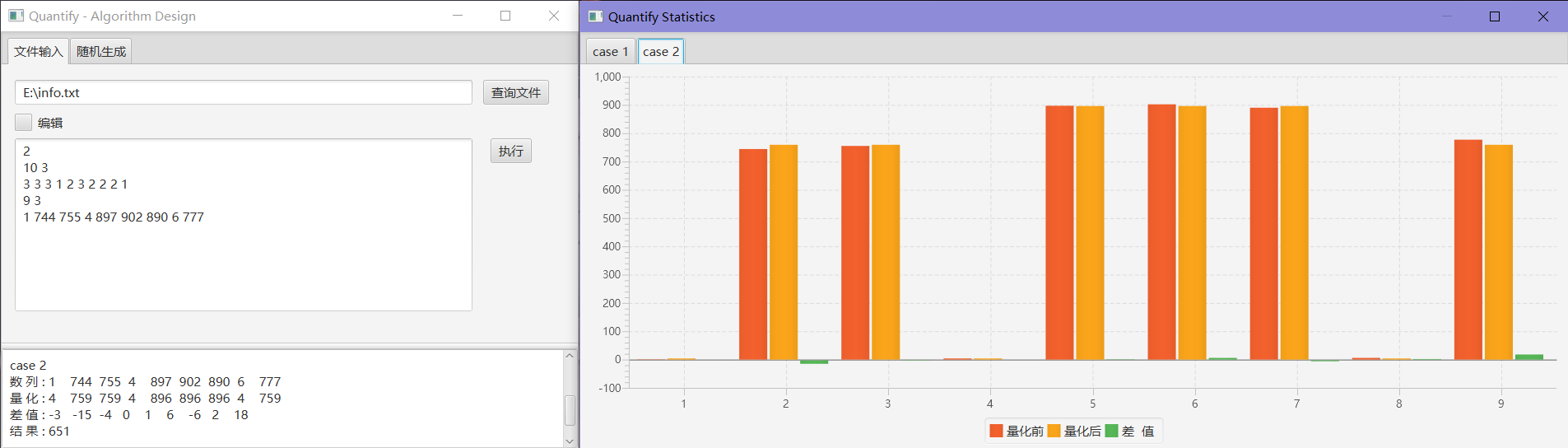
It is necessary to quantize the sequence of natural numbers less than 1000 into a sequence of s natural numbers. There are many ways to quantify, for example, only two numbers for the sequence {1 2 3 4 5 6 7 8 9 10}, can be expressed as {3 3 3 3 7 7 7 7 7}. Or can also be expressed in the form of {1 1 1 1 10 10 10 10 10}. What is the quantification result of the sum of the squares of the numerical errors?

For example, the sequence {1 2 3 4 5} is quantified to {2 2 3 3 3}, and the error after quantization is -1,0,0,1,2. Then the sum of the squared errors is 1 + 0 + 0 + 1 + 4 = 6. However, if the quantization becomes {2 2 4 4 4}, then the sum of the squares of errors is 1 + 0 + 1 + 0 + 1 = 3. Then write the program, use s values ​​to quantify the sum of the sum of the squares after the given sequence.

## Input

The first row enters the number of test cases C (1 <= C <= 50). The length n (1 <= n <= 100) of the first line of the test cases and the number of available values ​​s (1 <= s <= 10). The second line enters the n integer of the sequence, and all the numbers of the sequence are natural numbers below 1000.

## Output

Each test case will output the sum of the minimum squares generated when the given sequence is quantized with s values in one row.

# Example

## Input

```

2

10 3

3 3 3 1 2 3 2 2 2 1

9 3

1 744 755 4 897 902 890 6 777

```

## Output

```

0

651

```

# Code

 + [_C++_](https://github.com/InnoFang/Quantify/blob/master/code/quantify.cpp)

 + [_Java_](https://github.com/InnoFang/Quantify/blob/master/code/Quantify.java)

# GUI

 ![case1](https://cdn.jsdelivr.net/gh/innofang/quantify/image/case1.png)

  

  

 ![case2](https://cdn.jsdelivr.net/gh/innofang/quantify/image/case2.png)

 

# LICENSE

 [Apache License 2.0](https://github.com/InnoFang/Quantify/blob/master/LICENSE)