https://github.com/josecelano/php-mandelbrot-arbitrary-precision
PHP project to generate the Mandelbrot fractal using arbitrary precision math
https://github.com/josecelano/php-mandelbrot-arbitrary-precision
arbitrary-precision mandelbrot php
Last synced: 2 months ago
JSON representation
PHP project to generate the Mandelbrot fractal using arbitrary precision math
- Host: GitHub
- URL: https://github.com/josecelano/php-mandelbrot-arbitrary-precision
- Owner: josecelano
- Created: 2020-04-10T21:12:02.000Z (about 5 years ago)
- Default Branch: master
- Last Pushed: 2020-04-17T17:30:02.000Z (about 5 years ago)
- Last Synced: 2025-04-01T21:54:38.156Z (2 months ago)
- Topics: arbitrary-precision, mandelbrot, php
- Language: PHP
- Homepage:
- Size: 801 KB
- Stars: 1
- Watchers: 2
- Forks: 0
- Open Issues: 1
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Mandelbrot Kata
This a little programming exercise using the fractal domain, in particular the Mandelbrot Set.
Detailed explanations about the Mandelbrot Set can be found here:
https://en.wikipedia.org/wiki/Mandelbrot_set
The goals of the kata are:
* Understand a little bit the mathematical concepts behind fractals.
* Apply Test-First Programming approach.
* Improve OO programming skills.
In order to finish the kata you have to draw two versions of the Mandelbrot fractal:
* ASCII graph: see file `mandelbrot-160x160.txt`
* Image (background white and mandelbrot set in black): see file `mandelbrot-160x160.png`
### Math
Basically, there is a mathematical formula for complex number:
```
f(x) = z² + c
```
where `z` and `c` are complex number.
The Mandelbrot set is the set of complex numbers `c` for which the function does not diverge when iterated from z=0.
Than means, given a `c` complex number, if you apply the formula to that number `n` times using the previous result as the new `z` number, that `c` belongs to Mandelbrot Set if the sequence does not diverge.
You can represent those complex number in a graph where x-axis is the real part of the complex number and y-axis is the imaginary part.
### Drawing the fractal
You have to draw the portion of the graph between -2 and 2 real and imaginary parts.
Mandelbrot Set is inside those limits.
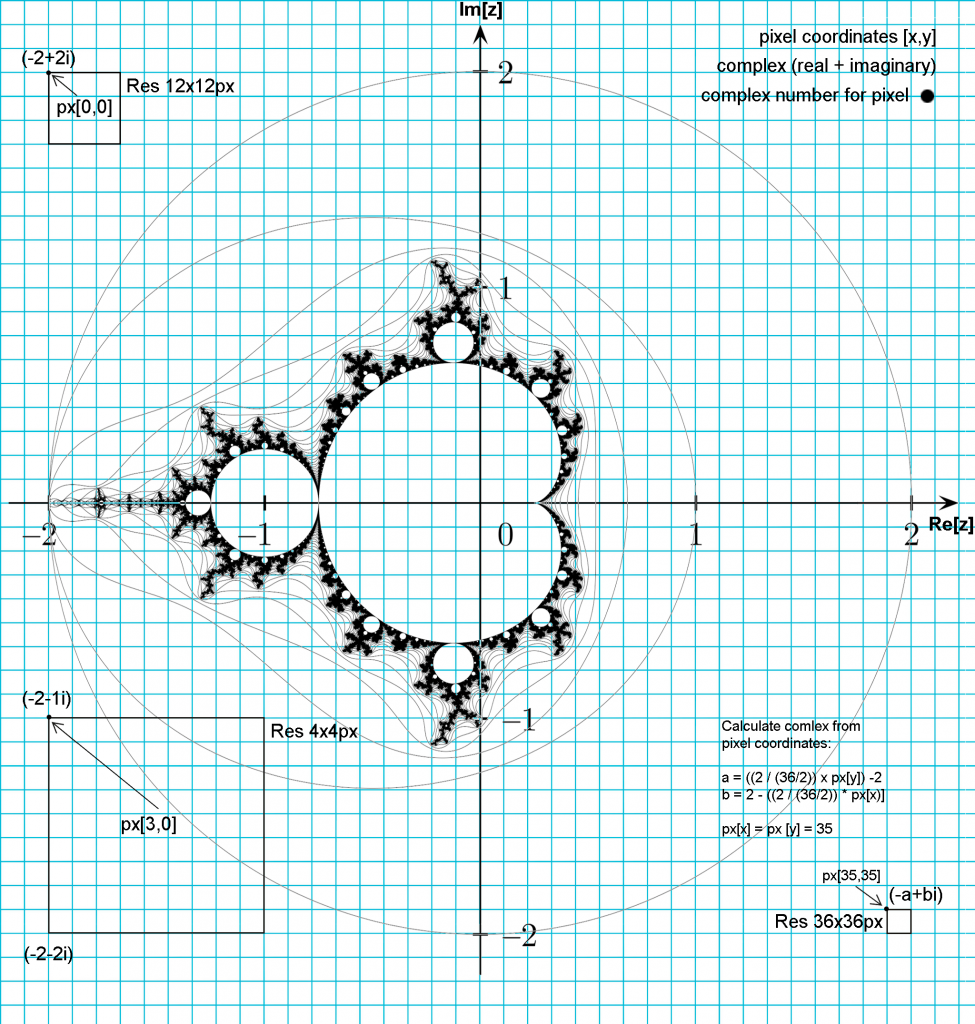
### Prerequisites
PHP
```
PHP 7.4
```
### Installation
PHP without docker
```
composer install
```
PHP with docker
```
docker build -t php-mandelbrot .
docker run -it --rm \
-v "$PWD":/usr/src/app \
-w /usr/src/app \
-u $(id -u ${USER}):$(id -g ${USER}) \
php-mandelbrot \
composer install
```
## Running the tests
PHP without docker
```
./vendor/bin/phpunit
```
PHP with docker
```
docker run -it --rm \
-v "$PWD":/usr/src/app \
-w /usr/src/app \
-u $(id -u ${USER}):$(id -g ${USER}) \
php-mandelbrot
```
Execute only one test class
```
docker run -it --rm \
-v "$PWD":/usr/src/app \
-w /usr/src/app \
-u $(id -u ${USER}):$(id -g ${USER}) \
php-mandelbrot \
./vendor/bin/phpunit --filter 'MandelbrotFormulaShould'
```
## Acknowledgments
* This kata was inspired by: https://github.com/edyoung/gnofract4d
## Similar projects
* https://github.com/ziqbal/mandelbrot
## Performance
It's very bad. It's not the goal of the project.
For 8192px image:
* Size: 8192x8192px
* Iter: 200
* Decimal precision: 28
* Time: 179m (2,98h)
* Performance: 0,17ms/px
* Min number step: 0,00048828125 (4/8192)
For 16384px image:
* Size: 16384x16384px
* Iter: 200
* Decimal precision: 28
* Time: 673m (11,21h)
* Performance: 0,17ms/px
* Min number step: 0,000244140625 (4/16384)
## TODO
Increase performance:
* Use [PHP parallel](https://www.php.net/manual/en/parallel.setup.php)
* Symmetry real axis.
* Mapping from pixel to complex number only for one image corner. Calculate next pixel complex from previous complex number.
More fun:
* Auto zoom.
* Build only the image for a tile.
* Add color map (grey scale).
* Add JS GUI like this: https://github.com/cslarsen/mandelbrot-js
Arbitrary precision:
* Test it with numbers greater than PHP float precision.