https://github.com/krichelj/pydiffgame
PyDiffGame is a Python implementation of a Nash Equilibrium solution to Differential Games, based on a reduction of Game Hamilton-Bellman-Jacobi (GHJB) equations to Game Algebraic and Differential Riccati equations, associated with Multi-Objective Dynamical Control Systems
https://github.com/krichelj/pydiffgame
artificial-intelligence-algorithms bellman-equation computer-science control-theory differential-equations differential-game dynamical-systems game-theory hamilton-jacobi-bellman hamiltonian inverted-pendulum matrix-equations multi-objective-optimization nash-equilibrium numerical-methods object-oriented-programming optimization-algorithms pontryagin-maximum-principle quadrotor riccati-equation
Last synced: 9 days ago
JSON representation
PyDiffGame is a Python implementation of a Nash Equilibrium solution to Differential Games, based on a reduction of Game Hamilton-Bellman-Jacobi (GHJB) equations to Game Algebraic and Differential Riccati equations, associated with Multi-Objective Dynamical Control Systems
- Host: GitHub
- URL: https://github.com/krichelj/pydiffgame
- Owner: krichelj
- License: mit
- Created: 2020-04-22T13:38:13.000Z (over 5 years ago)
- Default Branch: master
- Last Pushed: 2025-02-19T07:15:33.000Z (8 months ago)
- Last Synced: 2025-03-30T12:06:50.460Z (7 months ago)
- Topics: artificial-intelligence-algorithms, bellman-equation, computer-science, control-theory, differential-equations, differential-game, dynamical-systems, game-theory, hamilton-jacobi-bellman, hamiltonian, inverted-pendulum, matrix-equations, multi-objective-optimization, nash-equilibrium, numerical-methods, object-oriented-programming, optimization-algorithms, pontryagin-maximum-principle, quadrotor, riccati-equation
- Language: Python
- Homepage: https://krichelj.github.io/PyDiffGame/
- Size: 7.41 MB
- Stars: 50
- Watchers: 5
- Forks: 10
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- Contributing: CONTRIBUTING.md
- License: LICENSE
- Code of conduct: CODE_OF_CONDUCT.md
- Citation: CITATIONS.bib
Awesome Lists containing this project
README
[](https://opensource.org/licenses/MIT) [](https://github.com/krichelj/PyDiffGame/actions/workflows/python-publish.yml) [](https://github.com/krichelj/PyDiffGame/actions/workflows/pages/pages-build-deployment)
* [What is this?](#what-is-this)
* [Installation](#installation)
* [Input Parameters](#input-parameters)
* [Tutorial](#tutorial)
* [Authors](#authors)
* [Acknowledgments](#acknowledgments)
# What is this?
[`PyDiffGame`](https://github.com/krichelj/PyDiffGame) is a Python implementation of a Nash Equilibrium solution to Differential Games, based on a reduction of Game Hamilton-Bellman-Jacobi (GHJB) equations to Game Algebraic and Differential Riccati equations, associated with Multi-Objective Dynamical Control Systems\
The method relies on the formulation given in:
- The thesis work "_Differential Games for Compositional Handling of Competing Control Tasks_"
([Research Gate](https://www.researchgate.net/publication/359819808_Differential_Games_for_Compositional_Handling_of_Competing_Control_Tasks))
- The conference article "_Composition of Dynamic Control Objectives Based on Differential Games_"
([IEEE](https://ieeexplore.ieee.org/document/9480269) |
[Research Gate](https://www.researchgate.net/publication/353452024_Composition_of_Dynamic_Control_Objectives_Based_on_Differential_Games))
The package was tested for Python >= 3.10.
# Installation
To install this package run this from the command prompt:
```
pip install PyDiffGame
```
The package was tested for Python >= 3.10, along with the listed packages versions in [`requirments.txt`](https://github.com/krichelj/PyDiffGame/blob/master/requirements.txt)
# Input Parameters
The package defines an abstract class [`PyDiffGame.py`](https://github.com/krichelj/PyDiffGame/blob/master/src/PyDiffGame/PyDiffGame.py). An object of this class represents an instance of differential game.
The input parameters to instantiate a `PyDiffGame` object are:
* `A` : `np.array` of shape $(n,n)$
>System dynamics matrix
* `B` : `np.array` of shape $(n, m_1 + ... + m_N)$, optional
>Input matrix for all virtual control objectives
* `Bs` : `Sequence` of `np.array` objects of len $(N)$, each array $B_i$ of shape $(n,m_i)$, optional
>Input matrices for each virtual control objective
* `Qs` : `Sequence` of `np.array` objects of len $(N)$, each array $Q_i$ of shape $(n,n)$, optional
>State weight matrices for each virtual control objective
* `Rs` : `Sequence` of `np.array` objects of len $(N)$, each array $R_i$ of shape $(m_i,m_i)$, optional
>Input weight matrices for each virtual control objective
* `Ms` : `Sequence` of `np.array` objects of len $(N)$, each array $M_i$ of shape $(m_i,m)$, optional
>Decomposition matrices for each virtual control objective
* `objectives` : `Sequence` of `Objective` objects of len $(N)$, each $O_i$ specifying $Q_i, R_i$ and $M_i$, optional
>Desired objectives for the game
* `x_0` : `np.array` of len $(n)$, optional
>Initial state vector
* `x_T` : `np.array` of len $(n)$, optional
>Final state vector, in case of signal tracking
* `T_f` : positive `float`, optional
>System dynamics horizon. Should be given in the case of finite horizon
* `P_f` : `list` of `np.array` objects of len $(N)$, each array $P_{f_i}$ of shape $(n,n)$, optional, default = uncoupled solution of `scipy's solve_are`
>
>Final condition for the Riccati equation array. Should be given in the case of finite horizon
* `state_variables_names` : `Sequence` of `str` objects of len $(N)$, optional
>The state variables' names to display when plotting
* `show_legend` : `boolean`, optional
>Indicates whether to display a legend in the plots
* `state_variables_names` : `Sequence` of `str` objects of len $(n)$, optional
>The state variables' names to display
* `epsilon_x` : `float` in the interval $(0,1)$, optional
>Numerical convergence threshold for the state vector of the system
* `epsilon_P` : `float` in the interval $(0,1)$, optional
>Numerical convergence threshold for the matrices P_i
* `L` : positive `int`, optional
>Number of data points
* `eta` : positive `int`, optional
>The number of last matrix norms to consider for convergence
* `debug` : `boolean`, optional
>Indicates whether to display debug information
# Tutorial
To demonstrate the use of the package, we provide a few running examples.
Consider the following system of masses and springs:

The performance of the system under the use of the suggested method is compared with that of a Linear Quadratic Regulator (LQR). For that purpose, class named [`PyDiffGameLQRComparison`](https://github.com/krichelj/PyDiffGame/blob/master/src/PyDiffGame/PyDiffGameLQRComparison.py) is defined. A comparison of a system should subclass this class.
As an example, for the masses and springs system, consider the following instantiation of an [`MassesWithSpringsComparison`](https://github.com/krichelj/PyDiffGame/blob/master/src/PyDiffGame/examples/MassesWithSpringsComparison.py) object:
```python
import numpy as np
from PyDiffGame.examples.MassesWithSpringsComparison import MassesWithSpringsComparison
N = 2
k = 10
m = 50
r = 1
epsilon_x = 10e-8
epsilon_P = 10e-8
q = [[500, 2000], [500, 250]]
x_0 = np.array([10 * i for i in range(1, N + 1)] + [0] * N)
x_T = x_0 * 10 if N == 2 else np.array([(10 * i) ** 3 for i in range(1, N + 1)] + [0] * N)
T_f = 25
masses_with_springs = MassesWithSpringsComparison(N=N,
m=m,
k=k,
q=q,
r=r,
x_0=x_0,
x_T=x_T,
T_f=T_f,
epsilon_x=epsilon_x,
epsilon_P=epsilon_P)
```
Consider the constructor of the class `MassesWithSpringsComparison`:
```python
import numpy as np
from typing import Sequence, Optional
from PyDiffGame.PyDiffGame import PyDiffGame
from PyDiffGame.PyDiffGameLQRComparison import PyDiffGameLQRComparison
from PyDiffGame.Objective import GameObjective, LQRObjective
class MassesWithSpringsComparison(PyDiffGameLQRComparison):
def __init__(self,
N: int,
m: float,
k: float,
q: float | Sequence[float] | Sequence[Sequence[float]],
r: float,
Ms: Optional[Sequence[np.array]] = None,
x_0: Optional[np.array] = None,
x_T: Optional[np.array] = None,
T_f: Optional[float] = None,
epsilon_x: Optional[float] = PyDiffGame.epsilon_x_default,
epsilon_P: Optional[float] = PyDiffGame.epsilon_P_default,
L: Optional[int] = PyDiffGame.L_default,
eta: Optional[int] = PyDiffGame.eta_default):
I_N = np.eye(N)
Z_N = np.zeros((N, N))
M_masses = m * I_N
K = k * (2 * I_N - np.array([[int(abs(i - j) == 1) for j in range(N)] for i in range(N)]))
M_masses_inv = np.linalg.inv(M_masses)
M_inv_K = M_masses_inv @ K
if Ms is None:
eigenvectors = np.linalg.eig(M_inv_K)[1]
Ms = [eigenvector.reshape(1, N) for eigenvector in eigenvectors]
A = np.block([[Z_N, I_N],
[-M_inv_K, Z_N]])
B = np.block([[Z_N],
[M_masses_inv]])
Qs = [np.diag([0.0] * i + [q] + [0.0] * (N - 1) + [q] + [0.0] * (N - i - 1))
if isinstance(q, (int, float)) else
np.diag([0.0] * i + [q[i]] + [0.0] * (N - 1) + [q[i]] + [0.0] * (N - i - 1)) for i in range(N)]
M = np.concatenate(Ms,
axis=0)
assert np.all(np.abs(np.linalg.inv(M) - M.T) < 10e-12)
Q_mat = np.kron(a=np.eye(2),
b=M)
Qs = [Q_mat.T @ Q @ Q_mat for Q in Qs]
Rs = [np.array([r])] * N
R_lqr = 1 / 4 * r * I_N
Q_lqr = q * np.eye(2 * N) if isinstance(q, (int, float)) else np.diag(2 * q)
state_variables_names = ['x_{' + str(i) + '}' for i in range(1, N + 1)] + \
['\\dot{x}_{' + str(i) + '}' for i in range(1, N + 1)]
args = {'A': A,
'B': B,
'x_0': x_0,
'x_T': x_T,
'T_f': T_f,
'state_variables_names': state_variables_names,
'epsilon_x': epsilon_x,
'epsilon_P': epsilon_P,
'L': L,
'eta': eta}
lqr_objective = [LQRObjective(Q=Q_lqr,
R_ii=R_lqr)]
game_objectives = [GameObjective(Q=Q,
R_ii=R,
M_i=M_i) for Q, R, M_i in zip(Qs, Rs, Ms)]
games_objectives = [lqr_objective,
game_objectives]
super().__init__(args=args,
M=M,
games_objectives=games_objectives,
continuous=True)
```
Finally, consider calling the `masses_with_springs` object as follows:
```python
output_variables_names = ['$\\frac{x_1 + x_2}{\\sqrt{2}}$',
'$\\frac{x_2 - x_1}{\\sqrt{2}}$',
'$\\frac{\\dot{x}_1 + \\dot{x}_2}{\\sqrt{2}}$',
'$\\frac{\\dot{x}_2 - \\dot{x}_1}{\\sqrt{2}}$']
masses_with_springs(plot_state_spaces=True,
plot_Mx=True,
output_variables_names=output_variables_names,
save_figure=True)
```
This will result in the following plot that compares the two systems performance for a differential game vs an LQR:
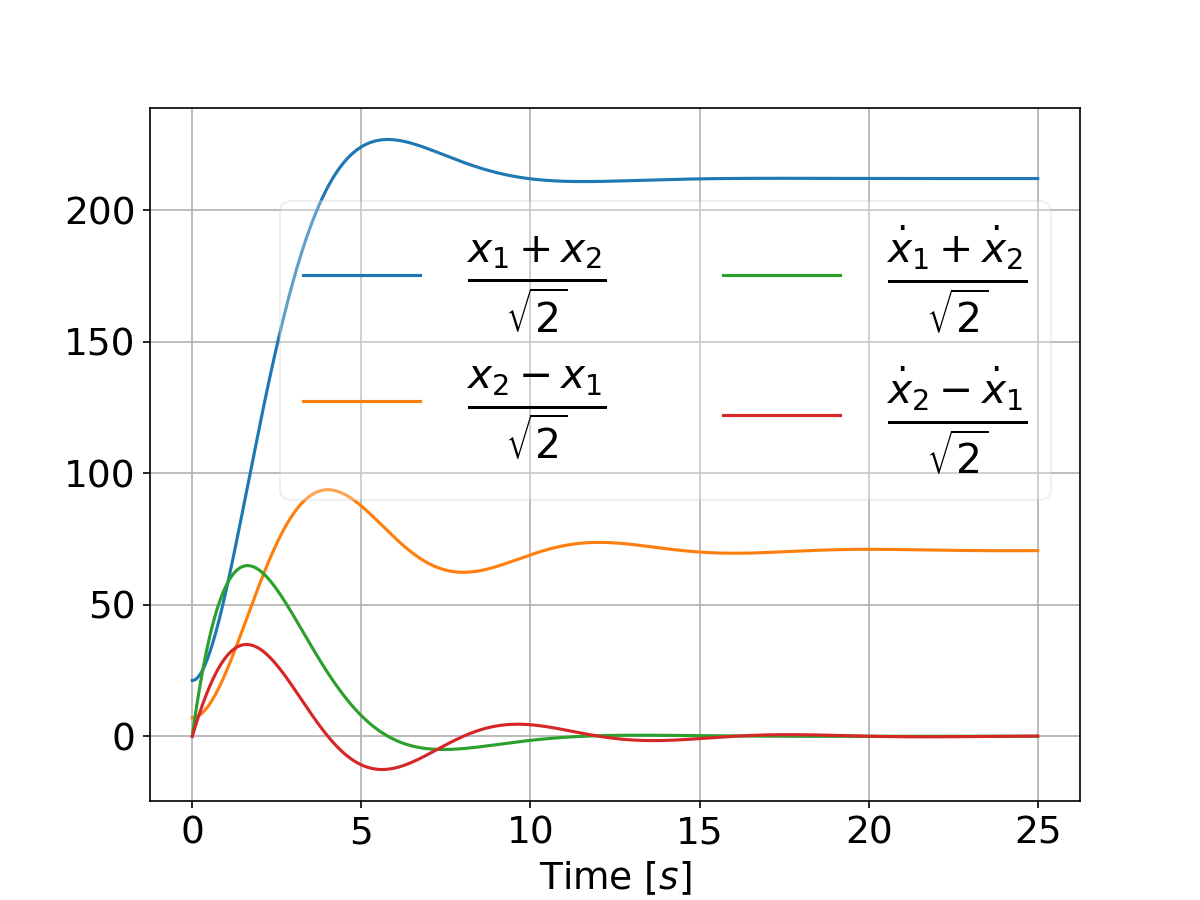
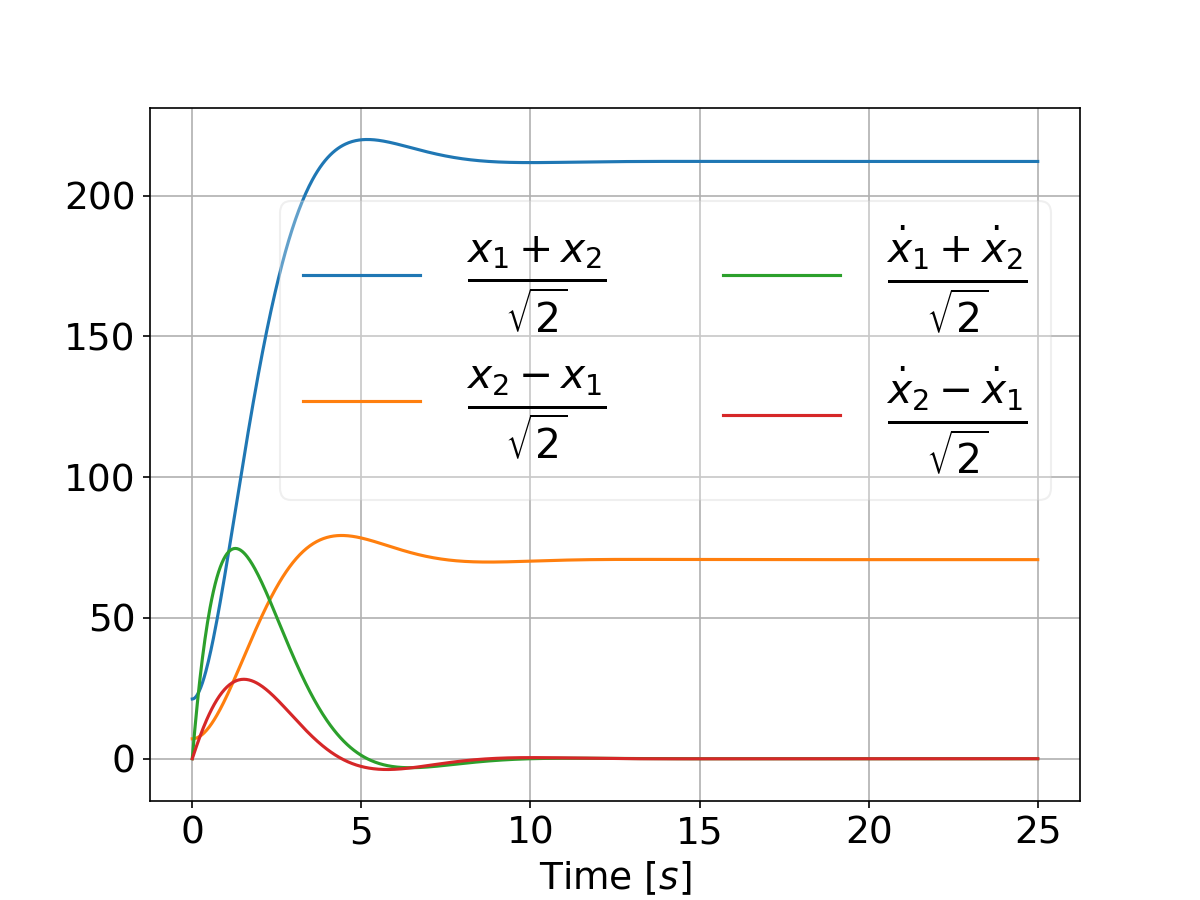
And when tweaking the weights by setting
```python
qs = [[500, 5000]]
```
we have:
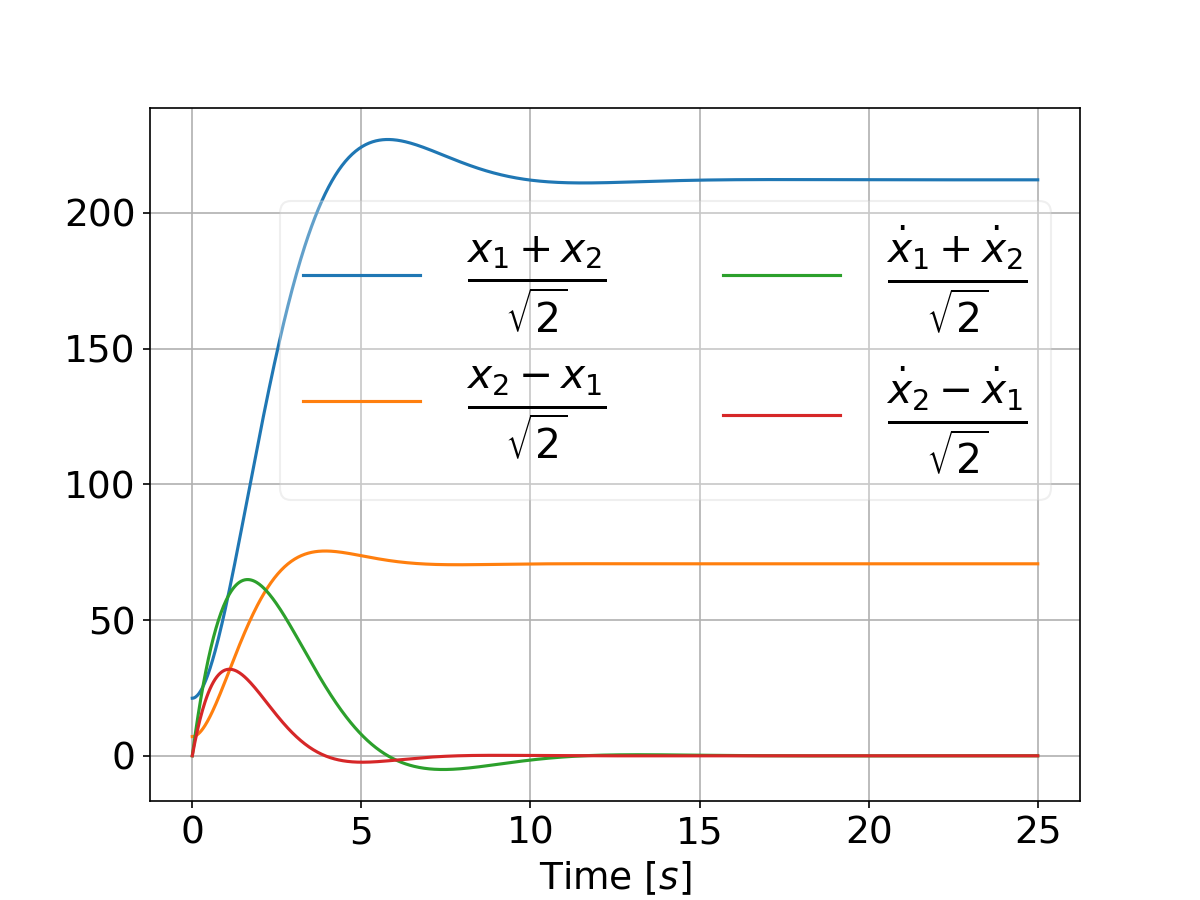
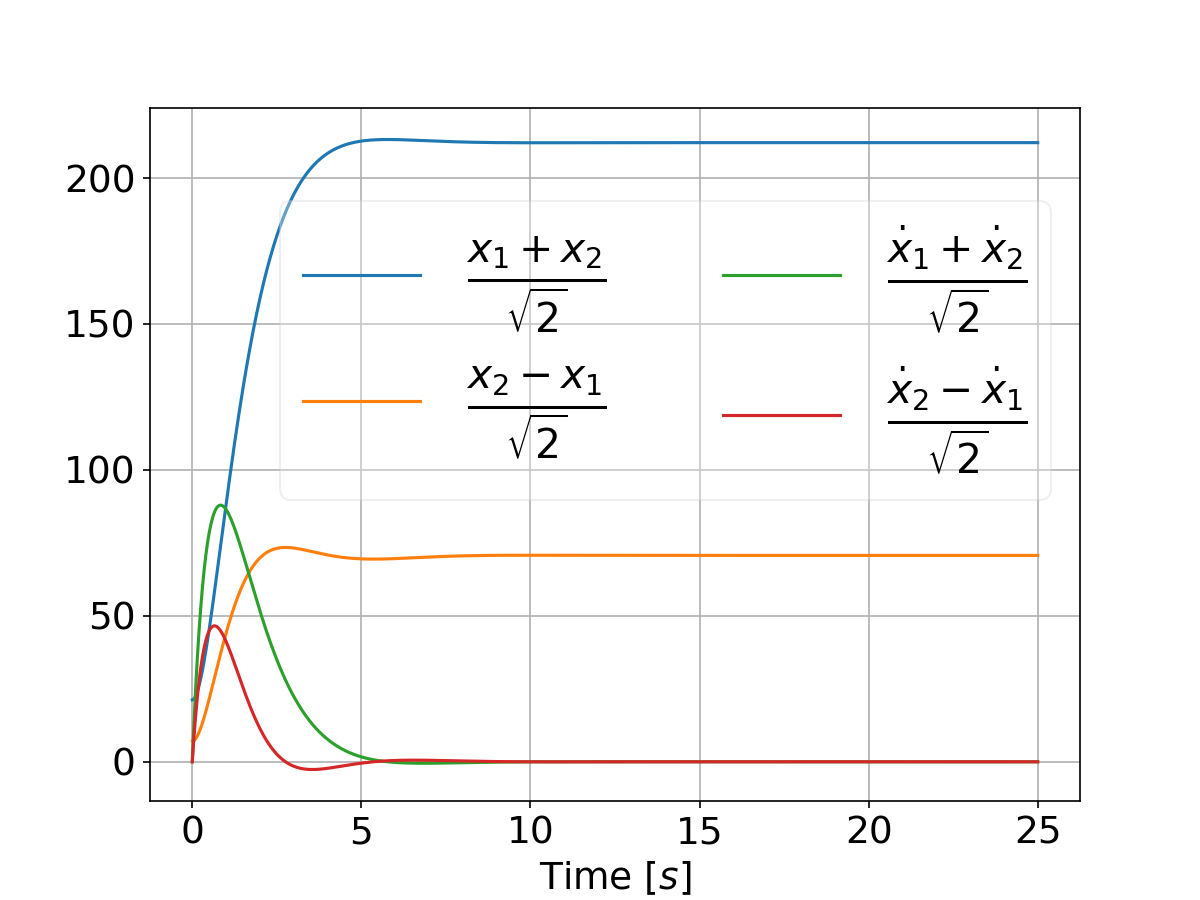
# Authors
If you use this work, please cite our paper:
```
@inproceedings{pydiffgame_paper,
author={Kricheli, Joshua Shay and Sadon, Aviran and Arogeti, Shai and Regev, Shimon and Weiss, Gera},
booktitle={29th Mediterranean Conference on Control and Automation (MED 2021)},
title={{Composition of Dynamic Control Objectives Based on Differential Games}},
year={2021},
volume={},
number={},
pages={298-304},
doi={10.1109/MED51440.2021.9480269}}
```
Further details can be found in the [citation document](CITATIONS.bib).
# Acknowledgments
This research was supported in part by the Leona M. and Harry B. Helmsley Charitable Trust through the '_Agricultural, Biological and Cognitive Robotics Initiative_' ('ABC') and by the Marcus Endowment Fund both at Ben-Gurion University of the Negev, Israel.
This research was also supported by The '_Israeli Smart Transportation Research Center_' ('ISTRC') by The Technion and Bar-Ilan Universities, Israel.