Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/krproject-tech/matlab_ancf_shell
Nonlinear shell dynamics analysis based on FEM shell element with Absolute Nodal Coordinate. Formulation (ANCF).
https://github.com/krproject-tech/matlab_ancf_shell
absolute-nodal-coordinate-formulation ancf dynamics fem finite-element-method matlab structure
Last synced: 17 days ago
JSON representation
Nonlinear shell dynamics analysis based on FEM shell element with Absolute Nodal Coordinate. Formulation (ANCF).
- Host: GitHub
- URL: https://github.com/krproject-tech/matlab_ancf_shell
- Owner: KRproject-tech
- License: mit
- Created: 2023-08-11T02:33:07.000Z (over 1 year ago)
- Default Branch: main
- Last Pushed: 2024-11-18T04:04:18.000Z (about 1 month ago)
- Last Synced: 2024-11-18T05:18:24.403Z (about 1 month ago)
- Topics: absolute-nodal-coordinate-formulation, ancf, dynamics, fem, finite-element-method, matlab, structure
- Language: MATLAB
- Homepage:
- Size: 32.6 MB
- Stars: 21
- Watchers: 1
- Forks: 1
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# MATLAB_ANCF_shell
Nonlinear plate dynamics analysis based on FEM shell element with Absolute Nodal Coordinate Formulation (ANCF) [^1].
(This code is validated with MATLAB R2007b or later versions)
**Communication**
**Language**
## Directory
├─Plate_FEM_explicit_3_SURFplot
│ ├─cores
│ │ ├─functions
│ │ ├─solver
│ │ └─ToolBoxes
│ └─save
│ └─fig
└─Plate_FEM_implicit_0
├─cores
│ ├─functions
│ ├─solver
│ └─ToolBoxes
└─save
└─fig
* __Plate_FEM_implicit_0__ : Implicit solver (Faster and more robust under the thin thickness condition)
* __Plate_FEM_explicit_3_SURFplot__ : Explicit solver (Light computing cost)
__Comparisons between Semi-implicit solver vs ODE113 (MATLAB explicit solver)__
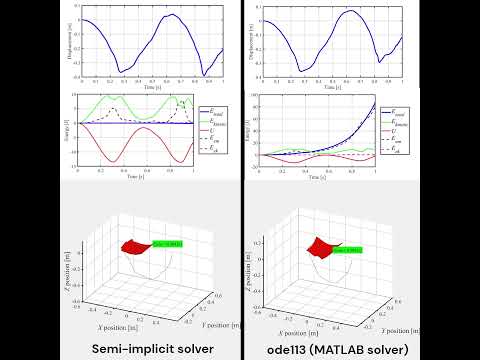[](https://youtube.com/shorts/R_YgaX05x_U?si=56Yt0fEM15mr7k4f)
## Publications
This code with the implicit solver (__Plate_FEM_implicit_0__) was employed as a structure solver for the following publication(s):
* Influence of the aspect ratio of the sheet for an electric generator utilizing the rotation of a flapping sheet, Mechanical Engineering Journal, Vol. 8, No. 1 (2021).
https://doi.org/10.1299/mej.20-00459
````
@article{Akio YAMANO202120-00459,
title={Influence of the aspect ratio of the sheet for an electric generator utilizing the rotation of a flapping sheet},
author={Akio YAMANO and Hiroshi IJIMA and Atsuhiko SHINTANI and Chihiro NAKAGAWA and Tomohiro ITO},
journal={Mechanical Engineering Journal},
volume={8},
number={1},
pages={20-00459-20-00459},
year={2021},
doi={10.1299/mej.20-00459}
}
````
* Flow-induced vibration and energy-harvesting performance analysis for parallelized two flutter-mills considering span-wise plate deformation with geometrical nonlinearity and three-dimensional flow, International Journal of Structural Stability and Dynamics, Vol. 22, No. 14, (2022).
https://doi.org/10.1142/S0219455422501632
````
@article{doi:10.1142/S0219455422501632,
author = {Yamano, Akio and Chiba, Masakatsu},
title = {Flow-Induced Vibration and Energy-Harvesting Performance Analysis for Parallelized Two Flutter-Mills Considering Span-Wise Plate Deformation with Geometrical Nonlinearity and Three-Dimensional Flow},
journal = {International Journal of Structural Stability and Dynamics},
volume = {22},
number = {14},
pages = {2250163},
year = {2022},
doi = {10.1142/S0219455422501632}
}
````
* Influence of boundary conditions on a flutter-mill, Journal of Sound and Vibration, Vol. 478, No. 21 (2020).
https://doi.org/10.1016/j.jsv.2020.115359
````
@article{YAMANO2020115359,
title = {Influence of boundary conditions on a flutter-mill},
journal = {Journal of Sound and Vibration},
volume = {478},
pages = {115359},
year = {2020},
doi = {https://doi.org/10.1016/j.jsv.2020.115359},
author = {A. Yamano and A. Shintani and T. Ito and C. Nakagawa and H. Ijima}
}
````
## Preparation before analysis
__[Step 1] Install the ToolBoxes__
The following ToolBoxes in “./XXXX/cores/ToolBoxes/” are required,
__For numerical analysis:__
* __“Meshing a plate using four noded elements”__ by KSSV:
https://jp.mathworks.com/matlabcentral/fileexchange/33731-meshing-a-plate-using-four-noded-elements
* __“Sparse sub access”__ by Bruno Luong:
https://jp.mathworks.com/matlabcentral/fileexchange/23488-sparse-sub-access
* __“Vectorized Multi-Dimensional Matrix Multiplication”__ by Darin Koblick:
https://jp.mathworks.com/matlabcentral/fileexchange/47092-vectorized-multi-dimensional-matrix-multiplication?s_tid=prof_contriblnk
__For plotting results:__
* __“mmwrite”__ by Micah Richert:
https://jp.mathworks.com/matlabcentral/fileexchange/15881-mmwrite
* __“mpgwrite”__ by David Foti:
https://jp.mathworks.com/matlabcentral/fileexchange/309-mpgwrite?s_tid=srchtitle
* __“mmread”__ by Micah Richert:
https://jp.mathworks.com/matlabcentral/fileexchange/8028-mmread
__[Step 1.2] Add path to installed ToolBoxes__
Modify "add_pathes.m" to add path to abovementined installed ToolBoxes as follows,
````
addpath ./cores/ToolBoxes/XX;
````
where `XX` is the name of folder of the installed ToolBox.
__[Step 2] Start GUI form__
Open the “GUI.fig” from MATLAB.
__[Step 2.1] Pre-setting__
Push the "Parameters" button and edit parameters.
__[Step 3] Start analysis__
Push the “exe” button and wait until the finish of the analysis.
__[Step 4] Plot results__
Push the “plot” button.
__[Step 5] View plotted results__
Results (figures and movie) plotted by [Step 4] are in "./save" directory.
## Parameters
Analytical condisions are in "./save/param_setting.m"
````
End_Time = 1.0; %% Analytical time [s]
d_t = 1e-4; %% step time [s]
core_num = 6; %% The number of CPUs for computing [-]
movie_format = 'mpeg'; %% movie format [-]
% movie_format = 'avi';
speed_check = 0; %%
%% Plate
rho_m = 1000; %% density [kg/m^3]
Eelastic = 1e+3; %% Young's modulus [Pa]
nu = 0.3; %% Poiison ratio [-]
Length = 100e-3; %% Length [m]
Width = 100e-3; %% Width [m]
thick = 10e-3; %% Thickness [m]
Nx = 8; %% The number of x-directional elements [-]
Ny = 8; %% The number of y-directional elements [-]
N_gauss = 5; %% Gauss-Legendre [-]
g = 9.81; %% gravity acc. [m/s^2]
F_in = -rho_m*g*[ 0 0 1].'; %% gravity [N/m^3]
````
and boundary conditions for nodes on the plate;
````
%% Boundary conditions
node_r_0 = [ 1]; %% Node number for fixed node [-]
node_dxr_0 = [ ]; %% Node number for fixed x-directional gradient [-]
node_dyr_0 = [ ]; %% Node number for fixed y-directional gradient [-]
````
Then, boundary conditions for a plate are written as,
* __Pinned at the corner of the plate__
````
%% Boundary conditions
node_r_0 = [ 1]; %% Node number for fixed node [-]
node_dxr_0 = [ ]; %% Node number for fixed x-directional gradient [-]
node_dyr_0 = [ ]; %% Node number for fixed y-directional gradient [-]
````
* __Clamped at the leading-edge__
````
%% Boundary conditions
node_r_0 = [ 1:Ny+1 ]; %% Node number giving the displacement constraint [-]
node_dxr_0 = [ 1:Ny+1 ]; %% Node number giving x-directional gradient constraint [-]
node_dyr_0 = [ 1:Ny+1 ]; %% Node number giving y-directional gradient constraint [-]
````
* __Pinned at the leading-edge__
````
%% Boundary conditions
node_r_0 = [ 1:Ny+1 ]; %% Node number giving the displacement constraint [-]
node_dxr_0 = [ ]; %% Node number giving x-directional gradient constraint [-]
node_dyr_0 = [ 1:Ny+1 ]; %% Node number giving y-directional gradient constraint [
````
where index in vector shows the node index around a plate element to apply boundary conditions.
## Gallery
* Young's modulus: $1.0 \times 10^5 \ \rm{Pa}$
* density: $7810 \ \rm{kg/m^3}$
* Poisson ratio: $0.3$
* Length, width: $0.3 \ \rm{m}$
* Thickness: $0.01 \ \rm{m}$
Deformed shape of the pendulum by this code ($8^2$ elements).
Deformed shape of the pendulum by this code ($12^2$ elements).
Deformed shape of the pendulum by the preceding report (Model I, $8^2$ elements, interpolated) [^2].
Time series of energy of the falling plate.
## Demonstration movie
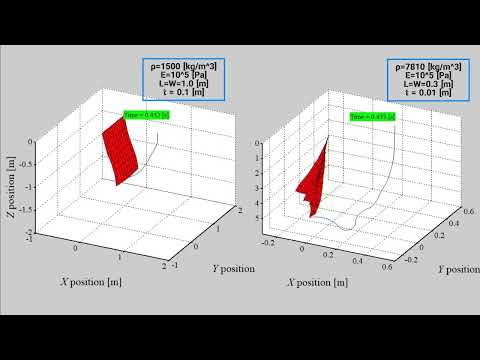[](https://www.youtube.com/watch?v=FohSLgNJ3vY)
## Stargazers over time
[](https://starchart.cc/KRproject-tech/MATLAB_ANCF_shell)
## License
MIT License
## Contributing
Issue reports and pull requests are highly welcomed.
### References
[^1]: A. Shabana, Computational Continuum Mechanics, Chap. 6 (Cambridge University Press, 2008), pp. 231–285.
[^2]: K. Dufva and A. Shabana, Analysis of thin plate structures using the absolute nodal coordinate formulation, Proc. IMechE Vol. 219 Part K: J. Multi-body Dynamics, 2005.