Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/markcmiller86/hello-numerical-world
https://github.com/markcmiller86/hello-numerical-world
Last synced: 9 days ago
JSON representation
- Host: GitHub
- URL: https://github.com/markcmiller86/hello-numerical-world
- Owner: markcmiller86
- Created: 2020-07-11T00:37:37.000Z (over 4 years ago)
- Default Branch: main
- Last Pushed: 2024-09-10T04:02:24.000Z (2 months ago)
- Last Synced: 2024-09-10T06:53:09.188Z (2 months ago)
- Language: C++
- Size: 2.67 MB
- Stars: 6
- Watchers: 3
- Forks: 6
- Open Issues: 3
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Hello Numerical World
For a complete, hands-on lesson involving this simple HPC/CSE application, please see the [ATPESC-2020 hands on lesson](lessons/hand_coded_heat/).
This is an implementation of an application for solving one dimensional heat conduction
problems. It is the functional equivalent of a *Hello World* application for HPC/CSE.
In general, heat [conduction](https://en.wikipedia.org/wiki/Thermal_conduction) is governed
by the partial differential equation ([PDE](https://en.wikipedia.org/wiki/Partial_differential_equation))...
| | |
|:---:|:---:|
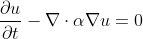||(1)|
where _u_ is the temperature at spatial positions, _x_, and times, _t_,
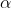 is the _thermal diffusivity_
of the material through which heat is flowing. This PDE
is known as the _Diffusion Equation_ and also the [_Heat Equation_](https://en.wikipedia.org/wiki/Heat_equation).
### Simplifying Assumptions
Our implemenation makes some simplifying assumptions...
1. The thermal diffusivity, ,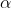
is constant for all _space_ and _time_.
1. The only heat _source_ is from the initial and/or boundary conditions.
1. We will deal only with the _one dimensional_ problem in _Cartesian coordinates_.
In this case, the PDE simplifies to...
| | |
|:---:|:---:|
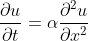||(2)|
From this highly simplified basic problem, there are a number of [extensions](http://hplgit.github.io/num-methods-for-PDEs/doc/pub/diffu/html/._diffu001.html) available for a more in-depth computational science study.
Currently, three different numerical algorithms are implemented here
* [Foward Time Centered Space (FTCS)](https://en.wikipedia.org/wiki/FTCS_scheme), an
[explicit](https://en.wikipedia.org/wiki/Explicit_and_implicit_methods) method
* [Crank-Nicholson](https://en.wikipedia.org/wiki/Crank–Nicolson_method),
an [implicit](https://en.wikipedia.org/wiki/Explicit_and_implicit_methods) method
* [Dufort-Frankel](http://folk.ntnu.no/leifh/teaching/tkt4140/._main064.html#ch5:sec42), another
[explicit](https://en.wikipedia.org/wiki/Explicit_and_implicit_methods) method
with higher temporal order than FTCS.
In addition, the application can be built with half, single, double and long-double precision.
Details are described more fully in this [ATPESC](https://extremecomputingtraining.anl.gov)
[Hands-On Lesson](https://josee1031.github.io/hello-numerical-world/lessons/hand_coded_heat/)
---
### Compiling and Using
The command...
```
make
```
will output help about available make targets.
```
Targets:
heat: makes the default heat application (double precision)
heat-omp: makes heat with OpenMP parallel threading (double precision)
heat-half: makes the heat application with half precision
heat-single: makes the heat application with single precision
heat-double: makes the heat application with double precision
heat-long-double: makes the heat application with long-double precision
PTOOL=[gnuplot,matplotlib,visit] RUNAME= plot: plots results
check: runs various tests confirming steady-state is linear
```
`make heat` will make the heat application with *default* (double) precision.
After making the application, the command...
```
./heat --help
```
gives help and example command-line argument usage...
```
Usage: ./heat = =...
runame="heat_results" name to give run and results dir (char*)
alpha=0.2 material thermal diffusivity (sq-meters/second) (fpnumber)
lenx=1 material length (meters) (fpnumber)
dx=0.1 x-incriment. Best if lenx/dx==int. (meters) (fpnumber)
dt=0.004 t-incriment (seconds) (fpnumber)
maxt=2 >0:max sim time (seconds) | <0:min l2 change in soln (fpnumber)
bc0=0 boundary condition @ x=0: u(0,t) (Kelvin) (fpnumber)
bc1=1 boundary condition @ x=lenx: u(lenx,t) (Kelvin) (fpnumber)
ic="const(1)" initial condition @ t=0: u(x,0) (Kelvin) (char*)
alg="ftcs" algorithm ftcs|dufrank|crankn (char*)
savi=0 save every i-th solution step (int)
save=0 save error in every saved solution (int)
outi=100 output progress every i-th solution step (int)
noout=0 disable all file outputs (int)
prec=2 precision 0=half/1=float/2=double/3=long double (int const)
Examples...
./heat dx=0.01 dt=0.0002 alg=ftcs
./heat dx=0.1 bc0=273 bc1=273 ic="spikes(273,5,373)"
```
### Plotting results
There are scripts for running [gnuplot](http://www.gnuplot.info), [matplotlib](https://matplotlib.org) and [VisIt](https://visit.llnl.gov) to produce curve plots of the results.
Whatever option you select, the associated tool must be in your path.
For example, to use `gnuplot`, use the command...
```
make PTOOL=gnuplot RUNAME=heat_results plot
```
Where the `RUNAME` option is the name of the directory/folder containing the results to be plotted.
### Setting the Initial Condition (`ic=`)
The initial condition argument, `ic=`, handles various cases...
* **Constant**, `ic="const(V)"`: Set initial condition to constant value, `V`
* **Ramp**, `ic="ramp(L,R)"`: Set initial condition to a linear ramp having value `L` @ `x=0` and `R` @ `x=L_x`.
* **Step**, `ic="step(L,Mx,R)"`: Set initial condition to a step function having value `L` for all `x=Mx`.
* **Random**, `ic="rand(S,B,A)"`: Set initial condition to random values in the range `[B-A,B+A]` using seed value `S`.
* **Sin**, `ic="sin(A,w)"`: Set initial condition to `A*sin(pi*w*x)`.
* **Spikes**, `ic="spikes(C,A0,X0,A1,X1,...)"`: Set initial condition to a constant value, `C` with any number of _spikes_ where each spike is the pair, `Ai` specifying the spike amplitude and `Xi` specifying its position in, `x`.
* **File**, `ic="file(foo.dat)"` : read initial condition data from the file `foo.dat`.
**Note**: The boundary condition arguments, `bc0=` and `bc1=` should be specified such that they *combine* smoothly with the specified initial condition.