https://github.com/matloff/fasteR
Fast Lane to Learning R!
https://github.com/matloff/fasteR
Last synced: 7 months ago
JSON representation
Fast Lane to Learning R!
- Host: GitHub
- URL: https://github.com/matloff/fasteR
- Owner: matloff
- Created: 2019-04-28T19:02:30.000Z (over 6 years ago)
- Default Branch: master
- Last Pushed: 2024-08-08T00:45:27.000Z (over 1 year ago)
- Last Synced: 2024-11-12T13:39:27.466Z (about 1 year ago)
- Language: R
- Size: 68.1 MB
- Stars: 985
- Watchers: 41
- Forks: 159
- Open Issues: 10
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
- my-awesome - matloff/fasteR - 08 star:1.1k fork:0.2k Fast Lane to Learning R! (R)
- jimsghstars - matloff/fasteR - Fast Lane to Learning R! (R)
README
# fasteR: Fast Lane to Learning R!
## *"Becoming productive in R, as fast as possible"*
### Norm Matloff, Prof. of Computer Science, UC Davis; [my bio](http://heather.cs.ucdavis.edu/matloff.html)
(See notice at the end of this document regarding copyright.)
This site is for those who know nothing of R, and maybe even nothing of
programming, and seek *QUICK, PAINLESS!* entree to the world of R.
* **FAST**: You'll already be doing good stuff in R -- useful data analysis
-- in your very first lesson.
* **For nonprogrammers:** If you're comfortable with navigating
the Web and viewing charts, you're fine. This tutorial is aimed
at you, not experienced C or Python coders.
* **Motivating:** Every lesson centers around a *real problem* to be
solved, on *real data*. The lessons do *not* consist of a few toy
examples, unrelated to the real world. The material is presented in a
conversational, story-telling manner.
* **Just the basics, no frills or polemics:**
- Notably, in the first few lessons, we do NOT use Integrated
Development Environments (IDEs). RStudio, ESS etc. are great, but
you shouldn't be burdened with learning R *and* learning an IDE at the
same time, a distraction from the goal of becoming productive in R as
fast as possible.
Note that even the excellent course by [R-Ladies
Sydney](https://threadreaderapp.com/thread/1119025557830684673.html),
which does start with RStudio, laments that RStudio can be
**"way too overwhelming."**
So, in the initial lessons, we stick to the R command line, and
focus on data analysis, not tools such as IDEs, which we will cover as
an intermediate-level topic. (Some readers of this tutorial may already
be using RStudio, in which case they will just run in the RS
Console pane.)
- Coverage is mainly limited to base R. So for instance the popular
but self-described "opinionated" Tidyverse is not treated, partly
due to its controversial nature (I am a
[skeptic](http://github.com/matloff/TidyverseSkeptic)), but
again mainly because it would be an obstacle to your
becoming productive in R quickly.
While you can learn a few simple, "sanitized" things in Tidy
quickly, thinking you are learning a lot, those things are quite
limited in scope, and Tidy learners often find difficulty in
applying R to real world situations. Our tutorial here is aimed
at learners whose goal is to *use the R system productively in
their own data analysis.*
- **Pro Tip sections:** Pitfalls, handy tricks, general advice.
* **Nonpassive approach:** Passive learning, just watching the screen,
is NO learning. Coding is not a "spectator sport"; you must try the
concepts yourself, nonpassively. So there will be occasional **Your
Turn** sections, in which you the learner must devise and try your own
variants on what has been presented. Sometimes the tutorial will be
give you some suggestions, but even then, you should cook up your own
variants to try. Remember: You get out what
you put in! The more actively you work the **Your Turn**
sections, the more powerful you will be as an R coder.
**HOW MUCH NEED YOU COVER?**
* Part I is basics, Part II advanced topics
* If you intend to cover only Part I, Lessons 1 through 11 should be
considered minimal.
## Table of Contents
**PART I**
* [Lesson 1: Getting Started](#overview)
* [Lesson 2: First R Steps](#firstr)
* [Lesson 3: Vectors and Indices](#vecidxs)
* [Lesson 4: More on Vectors](#less2)
* [Lesson 5: On to Data Frames!](#less3)
* [Lesson 6: The R Factor Class](#less4)
* [Lesson 7: Extracting Rows/Columns from Data Frames](#extractdf)
* [Lesson 8: More Examples of Extracting Rows, Columns](#moreextract)
* [Lesson 9: The tapply Function](#tapply)
* [Lesson 10: Data Cleaning](#less5)
* [Lesson 11: The R List Class](#less6)
* [Lesson 12: Another Look at the Nile Data](#less7)
* [Lesson 13: Pause to Reflect](#pause1)
* [Lesson 14: Introduction to Base R Graphics ](#less8)
* [Lesson 15: More on Base Graphics ](#less9)
* [Lesson 16: Writing Your Own Functions](#less10)
* [Lesson 17: `For` Loops](#less11)
* [Lesson 18: Functions with Blocks](#ftnbl)
* [Lesson 19: Text Editing and IDes](#edt)
* [Lesson 20: If, Else, Ifelse](#ifelse)
* [Lesson 21: Do Pro Athletes Keep Fit?](#keepfit)
* [Lesson 22: Linear Regression Analysis, I](#linreg1)
* [Lesson 23: S3 Classes](#s3)
* [Lesson 24: Baseball Player Analysis (cont'd.)](#less15)
* [Lesson 25: R Packages, CRAN, Etc.](#cran)
**PART II**
* [Lesson 26: A Pause, Before Going on to Advanced Topics](#advanced)
* [Lesson 27: A First Look at ggplot2](#gg2first)
* [Lesson 28: Should You Use Functional Programming?](#appfam)
* [Lesson 29 Simple Text Processing, I](#txt)
* [Lesson 30: Simple Text Processing, II](#txt1)
* [Lesson 31: Linear Regression Analysis, II](#linreg2)
* [Lesson 32: Working with the R Date Class](#dates)
* [Lesson 33: Tips on R Coding Style and Strategy](#style)
* [Lesson 34: The Logistic Model](#logit)
* [Lesson 35: Files and Directories](#fd)
* [Lesson 36: R `while` Loops](#whl)
* [To Learn More](#forMore)
* [Thanks](#thanks)
* [Appendix: Installing and Using RStudio](#rstudio)
For the time being, the main part of this online course will be this
**README.md** file. It is set up as a potential R package, though, and
I may implement that later.
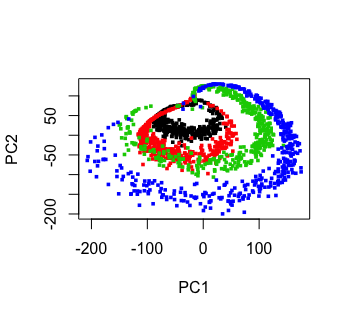
The color figure at the top of this file was generated by our
[**prVis** package](https://github.com/matloff/prVis/),
run on a famous dataset called *Swiss Roll*.
###
> 📘 Please note again, and KEEP IN MIND ALWAYS:
>
> * Nonpassive learning is absolutely key! So even if the output of an R
> command is shown here, run the command yourself in your R console, by
> copy-and-pasting from this document into the R console. Again, *you
> will get out of this tutorial what you put in.*
>
> * Similarly, the **Your Turn** sections are absolutely crucial. Devise
> your own little examples, and try them! "When in doubt, Try it
> out!" is a motto I devised for teaching. If you are unclear or
> curious about something, try it out! Just devise a little experiment,
> and type in the code. Don't worry -- you won't "break" things.
>
> * I cannot *teach* you how to
> program. I can merely give you the tools, e.g. R vectors, and some
> examples. For a given desired programming task, then, you must
> creatively put these tools together to attain the goal. Treat it like a
> puzzle! I think you'll find that if you stick with it, you'll find
> you're pretty good at it. After all, we can all work puzzles.
>
> * And for such reasons, one must remember that *there is not always a
> simple way to code a given task*. As you progress through these
> lessons, they will become increasingly complex. The essence of becoming
> a good programmer is to be patience and persistent. You then WILL
> complete those complex tasks!
### Starting out:
You'll need to [install
R](https://www.datacamp.com/community/tutorials/installing-R-windows-mac-ubuntu),
from [the R Project site](https://www.r-project.org). Start up R,
either by clicking an icon or typing `R` in a terminal window. We are
not requiring RStudio here, but if you already have it, start it; you'll
be typing into the R console, the Console pane.
As noted, this tutorial will be "bare bones." In particular, there is
no script to type your command for you. Instead, you will either
copy-and-paste from the text here into the R console, or type them there
by hand. (Note that the code lines here will all begin with the R
interactive prompt, `>`; that should not be typed.)
This is a Markdown file. You can read it right there on GitHub, which
has its own Markdown renderer. Or you can download it to your own
machine in Chrome and use the Markdown Reader extension to view it (be
sure to enable Allow Access to File URLs).
When you end your R session, exit by typing `quit()`.
Good luck! And if you have any questions, feel free to e-mail me, at
matloff@cs.ucdavis.edu
The R command prompt is `>`. Again, it will be shown here, but you don't type
it. It is just there in your R window to let you know R is inviting you
to submit a command. (If you are using RStudio, you'll see it in the
Console pane.)
So, just type `1+1` then hit Enter. Sure enough, it prints out 2 (you
were expecting maybe 12108?):
``` r
> 1 + 1
[1] 2
```
But what is that `[1]` here? It's just a row label. We'll go into that
later, not needed quite yet.
### Example: Nile River data
R includes a number of built-in datasets, mainly for illustration
purposes. One of them is **Nile**, 100 years of annual flow data on the
Nile River.
Let's find the mean flow:
``` r
> mean(Nile)
[1] 919.35
```
Here **mean** is an example of an R *function*, and in this case Nile is
an *argument* -- fancy way of saying "input" -- to that function. That
output, 919.35, is called the *return value* or simply *value*. The act
of running the function is termed *calling* the function. (Remember
these terms!)
Another point to note is that we didn't need to call R's **print**
function; the mean flow just printed out automatically. We will see the
reason for that shortly, but we could have typed,
``` r
> print(mean(Nile))
```
Function calls in R (and other languages) work "from the inside out."
Here we are asking R to find the mean of the Nile data (our inner call),
then print the result (the outer call, to the function **print**).
But whenever we are at the R `>` prompt, any expression we type will be
printed out anyway, so there is no need to call **print**.
Since there are only 100 data points here, it's not unwieldy to print
them out. Again, all we have to do is type `Nile`, no need to call
**print**:
``` r
> Nile
Time Series:
Start = 1871
End = 1970
Frequency = 1
[1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020
[16] 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 774 840
[31] 874 694 940 833 701 916 692 1020 1050 969 831 726 456 824 702
[46] 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759
[61] 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801
[76] 1040 860 874 848 890 744 749 838 1050 918 986 797 923 975 815
[91] 1020 906 901 1170 912 746 919 718 714 740
```
Now you can see how the row labels work. There are 15 numbers per row
here, so the second row starts with the 16th, indicated by `[16]`. The
third row starts with the 31st output number, hence the `[31]` and so
on. So, if we want to find, say, the 78th value, we look at the third
number in the row labeled [76], obtaining 874.
Note that a set of numbers such as **Nile** is called a *vector*. This
one is a special kind of vector, a *time series*, with each element of
the vector recording a particular point in time, here consisting of the
years 1871 through 1970. We thus know that this vector has length 100
elements. But in general, we can find the length of any vector by
calling the **length** function, e.g.
``` r
> length(Nile)
[1] 100
```
If you are ever unsure of the arguments a function has, R provides the
**args** function. For instance, we will later use the **sort**
function, which orders a set of numbers from lowest to highest (or vice
versa).
For example:
``` r
> sort(Nile)
[1] 456 649 676 692 694 698 701 702 714 718 726 740 742 744 744
[16] 746 749 759 764 768 771 774 781 796 797 799 801 812 813 815
[31] 821 822 824 831 832 833 838 840 845 845 845 846 848 860 862
[46] 864 865 874 874 890 897 901 906 912 916 918 919 923 935 940
[61] 944 958 960 963 969 975 984 986 994 995 1010 1020 1020 1020 1030
[76] 1040 1040 1050 1050 1100 1100 1100 1110 1120 1120 1140 1140 1150 1160 1160
[91] 1160 1170 1180 1210 1210 1220 1230 1250 1260 1370
```
(Again, the return value from the call to **sort** was printed out
automatically.)
We can query **sort**'s arguments:
``` r
> args(sort)
function (x, decreasing = FALSE, ...)
NULL
```
We see that the **sort** function has arguments named **x**
and **decreasing** (and more, actually, but put that aside for now).
### A first graph
R has great graphics, not only in base R but also in wonderful
user-contributed packages, such as **ggplot2** and **lattice**. But
we'll stick with base-R graphics for now, and save the more powerful yet
more complex **ggplot2** for a later lesson.
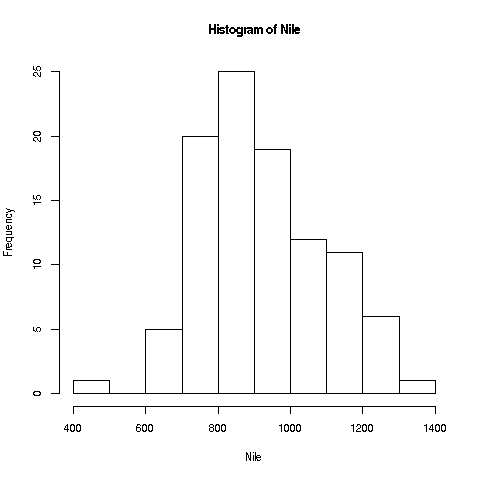
We'll start with a very simple, non-dazzling one, a no-frills histogram:
``` r
> hist(Nile)
```
Like any function, **hist** has a return value, but in this case, we
haven't save it. The return value contains the bin counts, bin
boundaries and so on.
> ❄️ Your Turn
>
> The *median* of a set of numbers is a value x such that half the
> numbers are less than x and half are greater than x. (There are issues
> with tied values, but not important here.) The median might be less
> than the mean or larger than it. Determine which of those two cases
> holds for the **Nile** data; the median function in R is of course
> named **median**.
>
> The **hist** function draws 10 bins for this dataset
> in the histogram by default, but you can choose other values, by
> specifying an optional second argument to the function, named
> **breaks**. E.g.
> ``` r
> > hist(Nile,breaks=20)
> ```
>
> would draw the histogram with 20 bins. Try plotting using several
> different large and small values of the number of bins.
**Note:** The **hist** function, as with many R functions, has many
different options, specifiable via various arguments. For now, we'll
just keep things simple, and resist the temptation to explore them all,
but R has lots of online help, which you can access via `?`. E.g.
typing
``` r
> ?hist
```
will tell you to full story on all the options available for the
**hist** function. Again, there are far too many for you to digest for
now (most users don't ever find a need for the more esoteric ones), but
it's a vital resource to know.
> 📘 Pro Tip
>
> Many people like to designate functions by adding parentheses. For
> instance, instead of writing something like, "The **length** function
> often comes in handy," they will write, "The **length()** function
> often comes in handy," in order to make sure others know they are
> talking about a function. I do that myself sometimes, but it can lead
> to trouble in some settings. Consider:
>
> ``` r
> > args(sort)
> function (x, decreasing = FALSE, ...)
> NULL
> > args(sort())
> Error in sort.default() : argument "x" is missing, with no default
> ```
>
> What went wrong? In the first case, we asked **args** about an object
> **sort** that happens to be of type 'function'. In the second case, we
> actually *called* **sort**. And the latter function itself expected an
> argument, which we did not supply. (And one wouldn't have been
> appropriate anyway.)
>
> The problem here was rather obvious--well, many things are "obvious"
> in retrospect, right?--, but it can occur much more
> subtly as well.
>
> This illustrates the point that in coding, one must be extremely careful
> in recognizing subtle differences, in this case between a *function* and
> a *call* to that function. In ordinary English, we might say, "That car
> wants to turn left" instead of "The *driver* of that car wants to turn
> left," but in coding we must be very picky.
> ❄️ Your Turn
>
> Write code to sort the **Nile** data from largest value to smallest,
> rather than vice versa.
>
> By default, calling **hist()** will display that graph, but we can
> suppress display, by setting one of its arguments. If we wish to save
> the return value of this function, we may wish to suppress the
> display. Check the online help to determine which argument does this,
> and verify that it works, i.e. it does suppress display.
>
> Look up the **order** function ('?order'), and try it out on the
> **Nile** data, and do a check that it is working as you expect.
>
## Lesson 3: Vectors and Indices
Say we want to find the mean river flow after year 1950.
The above output said that the **Nile** series starts in 1871. That
means 1951 will be the 81st year, and the 100th will be 1970. How do we
designate the 81st through 100th elements in this data?
Individual elements can be accessed using *subscripts* or *indices*
(singular is *index*), which are specified using brackets, e.g.
``` r
> Nile[2]
[1] 1160
```
for the second element (the output we saw earlier shows that the second
element is indeed 1160). The value 2 here is the index.
The **c** ("concatenate") function builds a vector, stringing several
numbers together. E.g. we can get the 2nd, 5th and 6th elements of
**Nile**:
``` r
> Nile[c(2,5,6)]
[1] 1160 1160 1160
```
If we wish to build a vector of *consecutive* numbers, we can use the
"colon" notation:
``` r
> Nile[c(2,3,4)]
[1] 1160 963 1210
> Nile[2:4]
[1] 1160 963 1210
```
As you can see, 2:4 is shorter way to specify the vector c(2,3,4).
So, 81:100 means all the numbers from 81 to 100. Thus
**Nile[81:100]** specifies the 81st through 100th elements in the **Nile**
vector.
Then to answer the above question on the mean flow during 1951-1971, we
can do
``` r
> mean(Nile[81:100])
[1] 877.05
```
> **NOTE:** Observe how the above reasoning process worked. We had a
> goal, to find the mean river flow after 1950. We knew we had some tools
> available to us, namely the **mean** function and R vector indices. We
> then had to figure out a way to combine these tools in a manner that
> achieves our goal, which we did.
>
> This is how use of R works in general. As you go through this tutorial,
> you'll add more and more to your R "toolbox." Then for any given goal,
> you'll rummage around in that toolbox, and eventually figure out the
> right set of tools for the goal at hand. Sometimes this will require
> some patience, but you'll find that the more you do, the more adept you
> become.
If we plan to do more with that time period, we should make a copy of
it:
``` r
> n81100 <- Nile[81:100]
> mean(n81100)
[1] 877.05
> sd(n81100)
[1] 125.5583
```
The function **sd** finds the standard deviation.
Note that we used R's *assignment operator* here to copy ("assign")
those particular **Nile** elements to **n81100**. (In most situations,
you can use `=` instead of `<-`, but why worry about what the exceptions
might be? They are arcane, so it's easier just to always use `<-`.
And though "keyboard shortcuts" for this are possible, again let's just
stick to the basics for now.)
Note too that though we will speak of the above operation as having
"extracted" the 81st through 100th elements of **Nile**, we have merely
made a copy of those elements. The original vector **Nile** remains
intact.
> 📘 Pro Tip
>
> We can pretty much choose any name we want; "n81100" just was chosen
> to easily remember this new vector's provenance. (But names can't
> include spaces, and must start with a letter.)
Note that **n81100** now is a 20-element vector. Its first element is
now element 81 of **Nile**:
``` r
> n81100[1]
[1] 744
> Nile[81]
[1] 744
```
Keep in mind that although **Nile** and **n81100** now have identical
contents, they are *separate* vectors; if one changes, the other will
not.
Recall that another oft-used function is **length**, which gives the
number of elements in the vector, e.g.
``` r
> length(Nile)
[1] 100
```
Can you guess the value of **length(n81100)**? Type this expression in
at the '>' prompt to check your answer.
> ❄️ Your Turn
>
> Write code to find the mean height of the Nile the
> over the years 1945-1960.
>
> In which period did the Nile have a larger mean height, the first 50
> years or the last 50?
### Recap: What have we learned in these first two lessons?
* Starting and exiting R.
* Some R functions: **mean**, **hist**, **length**.
* R vectors, and vector indices.
* Extracting vector subsets.
* Forming vectors, using the function **c** and ":".
Not a bad start! And needless to say, you'll be using all of these
frequently in the subsequent lessons and in your own usage of R.
Continuing along the Nile, say we would like to know in how many years
the level exceeded 1200. Let's first introduce R's **sum** function:
``` r
> sum(c(5,12,13))
[1] 30
```
Here the ***c*** function built a vector consisting of
5, 12 and 13. That vector was then fed into the **sum** function,
returning 5+12+13 = 30.
By the way, the above is our first example of *function composition*,
where the output of one function, ***c*** here, is fed as input into
another, **sum** in this case.
We can now use this to answer our question on the **Nile** data:
``` r
> sum(Nile > 1200)
[1] 7
```
The river level exceeded 1200 in 7 years.
**But how in the world did that work?** Bear with me a bit here. Let's
look at a small example first:
``` r
> x <- c(5,12,13)
> x
[1] 5 12 13
> x > 8
[1] FALSE TRUE TRUE
> sum(x > 8)
[1] 2
```
First, notice something odd here, in the expression **x > 8**. Here
**x** is a vector, 3 elements in length, but 8 is just a number. It
would seem that it's nnonsense to ask whether a vector is greater than a
number; they're different animals.
But R makes them "the same kind" of animal, by extending that number 8
to a 3-element vector 8,8,8. This is called *recycling*. This sets up
an element-by-element comparison: Then, the 5 in **x** is compared to
the first 8, yielding FALSE i.e. 5 is NOT greater than 8. Then 12 is
compared to the second 8, yielding TRUE, and then the comparison of 13
to the third 8 yields another TRUE. So, we get the vector
FALSE,TRUE,TRUE.
Fine, but how will **sum** add up some TRUEs and FALSEs? The
answer is that R, like most computer languages, treats TRUE and FALSE as
1 and 0, respectively. So we summed the vector (0,1,1), yielding 2.
Getting back to the question of the number of years in which the Nile
flow exceeded 1200, let's look at that expression again:
``` r
> sum(Nile > 1200)
```
Since the vector **Nile** has length 100, that number 1200 will be
recycled into a vector of one hundred copies of 1200. The '>'
comparison will then yield 100 TRUEs and FALSEs, so summing gives us the
number of TRUEs, exactly what we want.
A question related to *how many* years had a flow above 1200 is *which*
years had that property. Well, R actually has a **which** function:
``` r
> which(Nile > 1200)
[1] 4 8 9 22 24 25 26
```
So the 4th, 8th, 9th etc. elements in **Nile** had the queried property.
(Note that those were years 1874, 1878 and so on.)
In fact, that gives us another way to get the count of the years with
that trait:
``` r
> which1200 <- which(Nile > 1200)
> which1200
[1] 4 8 9 22 24 25 26
> length(which1200)
[1] 7
```
Of course, as usual, my choice of the variable name "which1200" was
arbirary, just something to help me remember what is stored in that
variable.
R's **length** function does what it says, i.e. finding the length of a
vector. In our context, that gives us the count of years with flow
above 1200.
And, what were the river flows in those 7 years?
``` r
> which1200 <- which(Nile > 1200)
> Nile[which1200]
[1] 1210 1230 1370 1210 1250 1260 1220
```
Finally, something a little fancier. We can combine steps above:
``` r
> Nile[Nile > 1200]
[1] 1210 1230 1370 1210 1250 1260 1220
```
We just "eliminated the middle man," **which1200**. The R interpreter
saw our "Nile > 1200", and thus generated the corresponding TRUEs and
FALSEs. The R interpreter then treated those TRUEs and
FALSEs as subscripts in **Nile**, thus extracting the desired data.
Now, we might add here, "Don't try this at home, kids." For
beginners, it's really easier and more comfortable to break things into
steps. Once, you become experienced at R, you may wish to start
skipping steps.
> ❄️ Your Turn
>
> Say we are interested in years in which the Nile had under 950. Write
> code to determine (a) how many such years there were, (b) which
> specific years these were, and (c) the median height during those
> years.
>
> Try a few other experiments of your choice using **sum**.
> I'd suggest starting with finding the sum of the first 25 elements in
> **Nile**. You may wish to start with experiments on a small vector, say
> (2,1,1,6,8,5), so you will know that your answers are correct.
> Remember, you'll learn best nonpassively. Code away!
>
> Also very useful is the notion of negative indices, e.g.
>
> ``` r
> > x <- c(5,12,13,8)
> > x[-1]
> [1] 12 13 8
> ```
>
> Here we are asking for all of **x** *except* for **x[1]**. Can you
> guess what **x[c(-1,-4)]** evaluates to? Guess first, then try it out.
Concerning that last point:
> 📘 Pro Tip
>
> A catchy motto I teach students is, "When in doubt, Try it out!" Get
> in the habit of devising little experiments that you can try to check
> the behavior of some R aspect that you are unsure of.
### Recap: What have we learned in this lesson?
Here you've refined your skillset for R vectors, learning R's recycling
feature, and two tricks that R users employ for finding counts of things.
Once again, as you progress through this tutorial, you'll see that these
things are used a lot in R.
## Lesson 5: On to Data Frames!
Right after vectors, the next major workhorse of R is the *data frame*.
It's a rectangular table consisting of one row for each data point.
Say we have height, weight and age on each of 100 people. Our data
frame would have 100 rows and 3 columns. The entry in, e.g., the second
row and third column would be the age of the second person in our data.
The second row as a whole would be all the data for that second person,
i.e. the height, weight and age of that person.
**Note that that row would also be considered a vector. The third column
as a whole would be the vector of all ages in our dataset.**
As our first example, consider the **ToothGrowth** dataset built-in to
R. Again, you can read about it in the online help by typing
``` r
> ?ToothGrowth
```
The data turn out to be on guinea pigs, with orange juice or
Vitamin C as growth supplements. Let's take a quick look
from the command line.
``` r
> head(ToothGrowth)
len supp dose
1 4.2 VC 0.5
2 11.5 VC 0.5
3 7.3 VC 0.5
4 5.8 VC 0.5
5 6.4 VC 0.5
6 10.0 VC 0.5
```
R's **head** function displays (by default) the first 6 rows of the
given dataframe. We see there are length, supplement and dosage
columns, which the curator of the data decided to name 'len', 'supp' and
'dose'. Each of column is an R vector, or in the case of the second
column, a vector-like object called a *factor*, to be discussed
shortly).
> 📘 Pro Tip
>
> To avoid writing out the long words repeatedly, it's handy to
> make a copy with a shorter name.
``` r
> tg <- ToothGrowth
```
Dollar signs are used to denote the individual columns, e.g.
**ToothGrowth$dose** for the dose column. So for instance, we can print
out the mean tooth length:
``` r
> mean(tg$len)
[1] 18.81333
```
Subscripts/indices in data frames are pairs, specifying row and column
numbers. To get the element in row 3, column 1:
``` r
> tg[3,1]
[1] 7.3
```
which matches what we saw above in our **head** example. Or, use the
fact that **tg$len** is a vector:
``` r
> tg$len[3]
[1] 7.3
```
The element in row 3, column 1 in the *data frame* **tg** is element 3
in the *vector* **tg$len**. This duality between data frames and
vectors is often exploited in R.
> ❄️ Your Turn
>
> The above examples are fundamental to R, so you should
> conduct a few small experiments on your own this time, little variants
> of the above. The more you do, the better!
For any subset of a data frame **d**, we can extract whatever rows and
columns we want using the format
``` r
d[the rows we want, the columns we want]
```
Some data frames don't have column names, but that is no obstacle. We
can use column numbers, e.g.
``` r
> mean(tg[,1])
[1] 18.81333
```
Note the expression '[,1]'. Since there is a 1 in the second position,
we are talking about column 1. And since the first position, before the
comma, is empty, no rows are specified -- so *all* rows are included.
That boils down to: all of column 1.
A key feature of R is that one can extract subsets of data frames,
just as we extracted subsets of vectors earlier. For instance,
``` r
> z <- tg[2:5,c(1,3)]
> z
len dose
2 11.5 0.5
3 7.3 0.5
4 5.8 0.5
5 6.4 0.5
```
Here we extracted rows 2 through 5, and columns 1 and 3, assigning the
result to **z**. To extract those columns but keep all rows, do
``` r
> y <- tg[ ,c(1,3)]
```
i.e. leave the row specification field empty.
By the way, note that the three columns are all of the same length, a
requirement for data frames. And what is that common length in this
case? R's **nrow** function tells us the number of rows in any data
frame:
``` r
> nrow(ToothGrowth)
[1] 60
```
Ah, 60 rows (60 guinea pigs, 3 measurements each).
Or, alternatively:
``` r
> tg <- ToothGrowth
> length(tg$len)
[1] 60
> length(tg$supp)
[1] 60
> length(tg$dose)
[1] 60
```
So now you know four ways to do the same thing. But isn't one enough?
Of course. But in this get-acquainted period, reading all four will
help reinforce the knowledge you are now accumulating about R. So,
*make sure you understand how each of those four approaches produced the
number 60.*
The **head** function works on vectors too:
``` r
> head(ToothGrowth$len)
[1] 4.2 11.5 7.3 5.8 6.4 10.0
```
Like many R functions, **head** has an optional second argument,
specifying how many elements to print:
``` r
> head(ToothGrowth$len,10)
[1] 4.2 11.5 7.3 5.8 6.4 10.0 11.2 11.2 5.2 7.0
```
You can create your own data frames -- good for devising little tests of
your understanding -- as follows:
``` r
> x <- c(5,12,13)
> y <- c('abc','de','z')
> d <- data.frame(x,y)
> d
x y
1 5 abc
2 12 de
3 13 z
```
Look at that second line! Instead of vectors consisting of numbers,
one can form vectors of character strings, complete with indexing
capability, e.g.
``` r
> y <- c('abc','de','z')
> y[2]
[1] "de"
```
As noted, all the columns in a data frame must be of the same length.
Here **x** consists of 3 numbers, and **y** consists of 3 character
strings. (The string is the unit in the latter. The number of
characters in each string is irrelevant.)
One can use negative indices for rows and columns as well, e.g.
``` r
> z <- tg[,-2]
> head(z)
len dose
1 4.2 0.5
2 11.5 0.5
3 7.3 0.5
4 5.8 0.5
5 6.4 0.5
6 10.0 0.5
```
> ❄️ Your Turn
>
> Devise your own little examples with the **ToothGrowth** data. For
> instance, write code that finds the number of cases in which the tooth
> length was less than 16, and which rows had the VC supplement..
>
> Also, try some examples with another built-in R dataset, **faithful**.
> This one involves the Old Faithful geyser in Yellowstone National Park
> in the US. The first column gives duration of the eruption, and the
> second has the waiting time since the last eruption.
>
> For instance, write code to find the maximum value of the durations,
> and also write code to determine the index (1st, 2nd, 3rd, ...) of
> that largest duration value.
>
> As mentioned, these operations are key features of R, so devise and
> run as many examples as possible; err on the side of doing too many!
### Recap: What have we learned in this lesson?
As mentioned, the data frame is the fundamental workhorse of R. It is
made up of columns of vectors (of equal lengths), a fact that often
comes in handy.
Unlike the single-number indices of vectors, each element in a data
frame has 2 indices, a row number and a column number. One can specify
sets of rows and columns to extra subframes.
One can use the R **nrow** function to query the number of rows in a
data frame; **ncol** does the same for the number of columns.
Each object in R has a *class*. The number 3 is of the **'numeric'**
class, the character string 'abc' is of the **'character'** class, and
so on. (In R, class names are quoted; one can use single or double
quotation marks.) Note that vectors of numbers are of **'numeric'**
class too; actually, a single number is considered to be a vector of
length 1. So, **c('abc','xw')**, for instance, is **'character'**
as well.
> 📘 Pro Tip
>
> Computers require one to be very, very careful and very, very precise.
> In that expression **c('abc','xw')** above, one might wonder why it does
> not evaluate to 'abcxw'. After all, didn't I say that the 'c' stands
> for "concatenate"? Yes, but the **c** function concatenates *vectors*.
> Here 'abc' is a vector of length 1 -- we have *one* character string,
> and the fact that it consists of 3 characters is irrelevant -- and
> likewise 'xw' is one character string. So, we are concatenating a
> 1-element vector with another 1-element vector, resulting in a 2-element
> vector.
What about **tg** and **tg$supp** in the Vitamin C example above? What
are their classes?
``` r
> class(tg)
[1] "data.frame"
> class(tg$supp)
[1] "factor"
```
R factors are used when we have *categorical* variables. If in a
genetics study, say, we have a variable for hair color, that might
comprise four categories: black, brown, red, blond. We can find the
list of categories for **tg$supp** as follows:
``` r
> levels(tg$supp)
[1] "OJ" "VC"
```
The categorical variable here is **supp**, the name the creator of this
dataset chose for the supplement column. We see that there are two categories
(*levels*), either orange juice or Vitamin C.
Note carefully that the values of an R factor must be quoted. Either
single or double quote marks is fine (though the marks don't show
up when we use **head**).
> 📘 Pro Tip
>
> The R **factor** class is one of the most powerful aspects of R. We
> will acquire this skill gradually in the coming lessons. Make sure to
> really become skilled in it.
> ❄️ Your Turn
>
> As mentioned, R includes many built-in datasets, a list of which you
> may obtain via the call **data()**. One of them is **CO2**. Using
> the **class()** function as above, determine which of the columns in
> this dataset, if any, are of **factor** class.
## Lesson 7: Extracting Rows/Columns from Data Frames
(The reader should cover this lesson especially slowly and carefully.
The concepts are simple, but putting them together requires careful
inspection.)
First, let's review what we saw in a previous lesson:
``` r
> which1200 <- which(Nile > 1200)
> Nile[which1200]
[1] 1210 1230 1370 1210 1250 1260 1220
```
There, we saw how to extract *vector elements*. We can do something
similar to extract *data frame rows or columns*. Here is how:
Continuing the Vitamin C example, let's compare mean tooth length for
the two types of supplements. Here is the code:
``` r
> whichOJ <- which(tg$supp == 'OJ')
> whichVC <- which(tg$supp == 'VC')
> mean(tg[whichOJ,1])
[1] 20.66333
> mean(tg[whichVC,1])
[1] 16.96333
```
In the first two lines above, we found which rows in **tg** (or
equivalently, which elements in **tg$supp**) had the OJ supplement, and
recorded those row numbers in **whichOJ**. Then we did the same for VC.
Now, look at the expression **tg[whichOJ,1]**. Remember, data frames
are accessed with two subscript expressions, one for rows, one for
colums, in the format
``` r
d[the rows we want, the columns we want]
```
So, **tg[whichOJ,1]** says to restrict attention to the OJ rows, and
only column 1, tooth length. We then find the mean of those restricted
numberss. This turned out to be 20.66333. Then do the same for VC.
Again, if we are pretty experienced, we can skip steps:
``` r
> tgoj <- tg[tg$supp == 'OJ',]
> tgvc <- tg[tg$supp == 'VC',]
> mean(tgoj$len)
[1] 20.66333
> mean(tgvc$len)
[1] 16.96333
```
Either way, we have the answer to our original question: Orange juice appeared
to produce more growth than Vitamin C. (Of course, one might form a
confidence interval for the difference etc.)
### Recap: What have we learned in this lesson?
Just as we learned earlier how to use a sequence of TRUE and FALSE
values to extract a parts of a vector, we now see how to do the
analogous thing for data frames: **We can use a sequence of TRUE and FALSE
values to extract a certain rows or columns from a data frame.**
It is imperative that the reader fully understand this lesson before
continuing, trying some variations of the above example on his/her own.
We'll be using this technique often in this tutorial, and it is central
to R usage in the real world.
> ❄️ Your Turn
>
> Try some of these operations on R's built-in **faithful** dataset.
> For instance, extract the sub-data frame consisting of all rows in
> which the waiting time was more than 80 minutes.
## Lesson 8: More Examples of Extracting Rows, Columns
Often we need to extract rows or columns from a data frame, subject to
more than one condition. For instance, say we wish to extract from
**tg** the sub-data frame consisting of rows in which
OJ was the treatment and length was less than 8.8.
We could do this, using the ampersand symbol '&', which means a logical
AND operation:
``` r
> tg[tg$supp=='OJ' & tg$len < 8.8,]
len supp dose
37 8.2 OJ 0.5
```
Ah, it turns out that only one case satisfied both conditions.
If we want all rows that satisfy at least one of the conditions, not
necessarily both, then we use the OR operator, '|'. Say we want to
obtain all rows in which either **len** is greater than 28 or the
treatment dose was 1.0 or both:
``` r
> tg[tg$len > 28 | tg$dose == 1.0,]
len supp dose
11 16.5 VC 1
12 16.5 VC 1
13 15.2 VC 1
14 17.3 VC 1
15 22.5 VC 1
16 17.3 VC 1
17 13.6 VC 1
18 14.5 VC 1
19 18.8 VC 1
20 15.5 VC 1
23 33.9 VC 2
26 32.5 VC 2
30 29.5 VC 2
41 19.7 OJ 1
42 23.3 OJ 1
43 23.6 OJ 1
44 26.4 OJ 1
45 20.0 OJ 1
46 25.2 OJ 1
47 25.8 OJ 1
48 21.2 OJ 1
49 14.5 OJ 1
50 27.3 OJ 1
56 30.9 OJ 2
59 29.4 OJ 2
```
By the way, note that the original row numbers are displayed too. For
example, the first case satisfying the conditions was row number 11 in
the original data frame **tg**.
Typically we want not only to extract part of the data frame, but also
save the results:
``` r
> w <- tg[tg$len > 28 | tg$dose == 1.0,]
```
Again, I chose the name 'w' arbitrarily. Names must begin with a
letter, and consist only of letters, digits and a few special
characters such as '-' or '.'
Note that **w** is a new data frame, on which we can perform the usual
operations, e.g.
``` r
> head(w)
len supp dose
11 16.5 VC 1
12 16.5 VC 1
13 15.2 VC 1
14 17.3 VC 1
15 22.5 VC 1
16 17.3 VC 1
> nrow(w)
[1] 25
```
We may only be interested in say, *how many* cases satisfied the given
conditions. As before, we can use **nrow** for that, as seen here.
As seen early, we can also extract columns. Say our analysis will use
only tooth length and dose. We write 'c(1,3)' in the "what columns we
want" place, indicating columns 1 and 3:
``` r
> lendose <- tg[,c(1,3)]
> head(lendose)
len dose
1 4.2 0.5
2 11.5 0.5
3 7.3 0.5
4 5.8 0.5
5 6.4 0.5
6 10.0 0.5
```
From now on, we would work with **lendose** instead of **tg**.
It's a little nicer, though, the specify the columns by name instead of
number:
``` r
> lendose <- tg[,c('len','dose')]
> head(lendose)
len dose
1 4.2 0.5
2 11.5 0.5
3 7.3 0.5
4 5.8 0.5
5 6.4 0.5
6 10.0 0.5
```
The logical operations work on vectors too. For example, say in the
**Nile** data we wish to know how many years had flows in the extremes,
say below 800 or above 1300:
``` r
> exts <- Nile[Nile < 800 | Nile > 1300]
> head(exts)
[1] 1370 799 774 694 701 692
> length(exts)
[1] 27
```
By the way, if this count were our only interest, i.e. we have no
further use for **exts**, we can skip assigning to **exts**, and do
things directly:
``` r
> length(Nile[Nile < 800 | Nile > 1300])
[1] 27
```
This is fine for advanced, experienced R users, but really, "one step at
a time" is better for beginners. It's clearer, and most important,
easier to debug if something goes wrong.
In the **Nile** data, say we are interested in the change in river
height from one year to the next. Recall the first few elements:
``` r
> head(Nile)
[1] 1120 1160 963 1210 1160 1160
```
So the was a change of +40, then a change of -197 and so on. How can we
code up a vector of all the changes?
``` r
> nile1 <- Nile[-1]
> head(nile1)
[1] 1160 963 1210 1160 1160 813
> z <- nile1 - Nile
Warning message:
In `-.default`(nile1, Nile) :
longer object length is not a multiple of shorter object length
> head(z)
[1] 40 -197 247 -50 0 -347
```
Let's ignore the warning for a moment. What happened here?
1. Deleting element 1 of **Nile** had the effect of shifting all the
elments leftward by one spot; i.e. **nile[1]** is **Nile[2][**,
**nile[2]** is **Nile[3]** and so on.
2. The subtraction **nile1 - Nile** is done element-by-element, so
it produced **nile1[1] - Nile[1]**, **nile1[2] - Nile[2]** etc.
But those are the year-to-year differences in the original **Nile**
data, so **z** now has exactly what we want!
3. But, that subtraction wasn't quite right. As the warning tells us,
we subtracted a vector of length 100 from one of length 99. R used
recycling to extend the latter to length 100, but the 100th element
of **z** is meaningless. We should probably finish by running
``` r
z <- z[-100]
```
In extracting various vector elements, rows or columns, we
don't have to use the same ordering, e.g.
``` r
> x <- c(5,12,13,8,168)
>
> x
[1] 5 12 13 8 168
> w <- x[c(5,4)]
> w
[1] 168 8
> x[c(4,5)] <- w
> x
[1] 5 12 13 168 8
```
We extracted the 5th and 4th elements of **x**, in that order. We
then assigned the result to **w**, and (whether we had some purpose in
mind or just for fun), we assigned the reversed numbers back into **x**.
Nor do the extracted entities need to be contiguous, e.g.
``` r
> x[c(1,4)]
[1] 5 168
```
### Recap: What we've learned in this lesson
Here we got more practice in manipulating data frames, and were
introduced to the logical operators '&' and '|'. We also saw another
example of using **nrow** as a means of counting how many rows satisfy
given conditions.
Again, these are all "bread and butter" operations that arise quite
freqently in real world R usage.
By the way, note how the essence of R is "combining little things in
order to do big things," e.g. combining the subsetting operation, the
'&' operator, and **nrow** to get a count of rows satisfying given
conditions. This too is the "bread and butter" of R. It's up to you,
the R user, to creatively combine R's little operations (and later, some
big ones) to achieve whatever goals you have for your data. *Programming
is a creative process*. It's like a grocery store and cooking: The
store has lots of different potential ingredients, and you decide which
ones to buy and combine into a meal.
> ❄️ Your Turn
> Try some of these operations on R's built-in **faithful** dataset.
>
> 1. Find the number of rows for which the **eruptions**
> column was greater than 3 and waiting time was more than 80 minutes.
>
> 2. Add code to print out the row numbers of those cases.
>
## Lesson 9: The tapply Function
> 📘 Pro Tip
>
> Often in R there is a shorter, more
> compact way of doing things. That's the case here; we can use the
> magical **tapply** function in the above example. In fact, we can do it
> in just one line.
The general form of a call to **tapply** is
``` r
tapply(what to split, what criterion to use for splitting,
what to do with the resulting grouped data)
```
``` r
> tapply(tg$len,tg$supp,mean)
OJ VC
20.66333 16.96333
```
In English: "Split the vector **tg$len** into two groups, according to
the value of **tg$supp**, then apply **mean** to each group." Note that
the result was returned as a vector, which we could save by assigning it
to, say **z**:
``` r
> z <- tapply(tg$len,tg$supp,mean)
> z[1]
OJ
20.66333
> z[2]
VC
16.96333
```
By the way, **z** is not only a vector, but also a *named* vector,
meaning that its elements have names, in this case 'OJ' and 'VC'.
Saving can be quite handy, because we can use that result in subsequent
code.
To make sure it is clear how this works, let's look at a small
artificial example:
``` r
> x <- c(8,5,12,13)
> g <- c('M',"F",'M','M')
```
Suppose **x** is the ages of some kids, who are a boy, a girl, then two more
boys, as indicated in **g**. For instance, the 5-year-old is a girl.
Let's call **tapply**:
``` r
> tapply(x,g,mean)
F M
5 11
```
That call said, "Split **x** into two piles, according to the
corresponding elements of **g**, and then find the mean in each pile.
Note that it is no accident that **x** and **g** had the same number of
elements above, 4 each. If on the contrary, **g** had 5 elements, that
fifth element would be useless -- the gender of a nonexistent fifth
child's age in **x**. Similarly, it wouldn't be right if **g** had had
only 3 elements, apparently leaving the fourth child without a specified
gender.
> 📘 Pro Tip
>
> If **g** had been of the wrong length, we would have gotten an error,
> "Arguments must be of the same length." This is a common error in R
> code, so watch out for it, keeping in mind WHY the lengths must be the
> same.
Instead of **mean**, we can use any function as that third argument in
**tapply**. Here is another example, using the built-in dataset
**PlantGrowth**:
``` r
> tapply(PlantGrowth$weight,PlantGrowth$group,length)
ctrl trt1 trt2
10 10 10
```
Here **tapply** split the **weight** vector into subsets according to
the **group** variable, then called the **length** function on each
subset. We see that each subset had length 10, i.e. the experiment had
assigned 10 plants to the control, 10 to treatment 1 and 10 to treatment
2.
> ❄️ Your Turn
>
> One of the most famous built-in R datasets is
> **mtcars**, which has various measurements on cars from the 60s and 70s.
> Lots of opportunties for you to cook up little experiments here!
>
> You may wish to start by comparing the mean miles-per-gallon values
> for 4-, 6- and 8-cylinder cars. Another suggestion would be to find
> how many cars there are in each cylinder category, using **table**.
> As usual, the more examples you cook up here, the better!
By the way, the **mtcars** data frame has a "phantom" column.
``` r
> head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
```
That first column seems to give the make (brand) and model of the car.
Yes, it does -- but it's not a column. Behold:
``` r
> head(mtcars[,1])
[1] 21.0 21.0 22.8 21.4 18.7 18.1
```
Sure enough, column 1 is the mpg data, not the car names. But we see
the names there on the far left! The resolution of this seeming
contradiction is that those car names are the *row names* of this data
frame:
``` r
> row.names(mtcars)
[1] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710"
[4] "Hornet 4 Drive" "Hornet Sportabout" "Valiant"
[7] "Duster 360" "Merc 240D" "Merc 230"
[10] "Merc 280" "Merc 280C" "Merc 450SE"
[13] "Merc 450SL" "Merc 450SLC" "Cadillac Fleetwood"
[16] "Lincoln Continental" "Chrysler Imperial" "Fiat 128"
[19] "Honda Civic" "Toyota Corolla" "Toyota Corona"
[22] "Dodge Challenger" "AMC Javelin" "Camaro Z28"
[25] "Pontiac Firebird" "Fiat X1-9" "Porsche 914-2"
[28] "Lotus Europa" "Ford Pantera L" "Ferrari Dino"
[31] "Maserati Bora" "Volvo 142E"
```
So 'Mazda RX4' was the *name* of row 1, but not part of the row.
As with everything else, **row.names** is a function, and as you can see
above, its return value here is a 32-element vector (the data frame had
32 rows, thus 32 row names). The elements of that vector are of class
**'character'**, as is the vector itself.
You can even assign to that vector:
``` r
> row.names(mtcars)[7]
[1] "Duster 360"
> row.names(mtcars)[7] <- 'Dustpan'
> row.names(mtcars)[7]
[1] "Dustpan"
```
Inside joke, by the way. Yes, the example is real and significant, but
the "Dustpan" thing came from a funny TV commercial at the time.
(If you have some background in programming, it may appear odd to you to
have a function call on the *left* side of an assignment. This is
actually common in R. It stems from the fact that '<-' is actually a
function! But this is not the place to go into that.)
> 📘 Pro Tip
>
> As a beginner (and for that matter later on), you should NOT be obsessed
> with always writing code in the "optimal" way, including in terms of
> compactness of the code. It's much more important
> to write something that works and is clear; one can always tweak it
> later. In this case, though, **tapply** actually aids clarity, and it
> is so ubiquitously useful that we have introduced it early in this
> tutorial. We'll be using it more in later lessons.
Most real-world data is "dirty," i.e. filled with errors. The famous
[New York taxi trip
dataset](https://data.cityofnewyork.us/Transportation/2017-Yellow-Taxi-Trip-Data/biws-g3hs),
for instance, has one trip destination whose lattitude and longitude
place it in Antartica! The impact of such erroneous data on one's statistical
analysis can be anywhere from mild to disabling. Let's see below how one
might ferret out bad data. And along the way, we'll cover several new R
concepts.
We'll use the famous Pima Diabetes dataset. Various versions exist, but
we'll use the one included in **faraway**, an R package compiled
by Julian Faraway, author of several popular books on statistical
regression analysis in R.
I've placed the data file, **Pima.csv**, on
[my Web site](http://heather.cs.ucdavis.edu/FasteR/data/Pima.csv). Here
is how you can read it into R:
``` r
> pima <- read.csv('http://heather.cs.ucdavis.edu/FasteR/data/Pima.csv',header=TRUE)
```
The dataset is in a CSV ("comma-separated values") file. Here we read
it, and assigned the resulting data frame to a variable we chose to name
**pima**.
Note that second argument, **header=TRUE**. A header in a file, if one
exists, is in the first line in the file. It states what names the
columns in the data frame are to have. If the file doesn't have one,
set **header** to FALSE. You can always add names to your data frame
later (future lesson).
> 📘 Pro Tip
>
> It's always good to take a quick look at a newly loaded or construced
> data frame:
``` r
> head(pima)
pregnant glucose diastolic triceps insulin bmi diabetes age test
1 6 148 72 35 0 33.6 0.627 50 1
2 1 85 66 29 0 26.6 0.351 31 0
3 8 183 64 0 0 23.3 0.672 32 1
4 1 89 66 23 94 28.1 0.167 21 0
5 0 137 40 35 168 43.1 2.288 33 1
6 5 116 74 0 0 25.6 0.201 30 0
> dim(pima)
[1] 768 9
```
The **dim** function tells us that there are
768 people in the study, 9 variables measured on each, i.e. the data has
768 rows and 9 columns.
Since this is a study of diabetes, let's take a look at the glucose
variable. R's **table** function is quite handy.
``` r
> table(pima$glucose)
0 44 56 57 61 62 65 67 68 71 72 73 74 75 76 77 78 79 80 81
5 1 1 2 1 1 1 1 3 4 1 3 4 2 2 2 4 3 6 6
82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101
3 6 10 7 3 7 9 6 11 9 9 7 7 13 8 9 3 17 17 9
102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121
13 9 6 13 14 11 13 12 6 14 13 5 11 10 7 11 6 11 11 6
122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141
12 9 11 14 9 5 11 14 7 5 5 5 6 4 8 8 5 8 5 5
142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161
5 6 7 5 9 7 4 1 3 6 4 2 6 5 3 2 8 2 1 3
162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181
6 3 3 4 3 3 4 1 2 3 1 6 2 2 2 1 1 5 5 5
182 183 184 186 187 188 189 190 191 193 194 195 196 197 198 199
1 3 3 1 4 2 4 1 1 2 3 2 3 4 1 1
```
Be careful here; the first, third, fifth and so on lines are the glucose
values, while the second, fourth, sixth and so on lines are the counts
of women having those values. For instance, 3 women had glucose = 68.
Uh, oh! 5 women in the study had glucose level 0. And 1 had level 44,
etc. Presumably 0 is not physiologically possible, and maybe not 44
either.
Let's consider a version of the glucose data that at least excludes these 0s.
``` r
> pg <- pima$glucose
> pg1 <- pg[pg > 0]
> length(pg1)
[1] 763
```
As before, the expression **pg > 0** creates a vector of TRUEs and FALSEs.
The filtering **pg[pg > 0]** will only pick up the TRUE cases, and sure
enough, we see that **pg1** has only 763 cases, as opposed to the
original 768; the 5 with glucose = 0 are now gone.
Did removing the 0s make much difference? Turns out it doesn't:
``` r
> mean(pg)
[1] 120.8945
> mean(pg1)
[1] 121.6868
```
But still, these things can in fact have major impact in many
statistical analyses.
R has a special code for missing values, NA, for situations like this.
Rather than removing the 0s, it's better to recode them as NAs. Let's
do this, back in the original dataset so we keep all the data in
one object:
``` r
> pima$glucose[pima$glucose == 0] <- NA
```
This is a bit complicated. Here is the same action, but broken into
smaller steps:
``` r
> glc <- pima$glucose
> z <- glc == 0
> glc[z] <- NA
> pima$glucose <- glc
```
Here is what the code does:
- That first line just makes a copy of the original vector, to avoid
clutter in the code.
- The second line determines which elements of **glc**
are 0s, resulting in **z** being a vector of TRUEs and FALSEs.
- The third line then assigns NA to those elements in **glc** corresponding to
the TRUEs. (Note the recycling of NA.)
- Finally, we need to have the changes in the original data, so we copy
**glc** to it.
> 📘 Pro Tip
>
> We broke our original 1 line of code into 4 simpler lines.
> This is MUCH clearer, and by the way, easier to debug.
> I recommend this especially for beginners, but also for everyone, and
> I use this approach a lot in my own code.
>
> There is an advanced R concept, *pipes*, that also breaks longer
> computations into smaller steps. I do not use pipes (either the
> Tidyverse version or the newer base-R pipes), as I believe they are
> less clear and, very important, hard to debug. You may find you like
> them, which of course is fine, but we will not use them here.
> 📘 Pro Tip
>
> Note again the double-equal sign in the above code! If we wish to
> test whether, say, ***a*** and ***b*** are equal, the expression must
> be "a == b", not "a = b"; the latter would do "a <- b". This is a
> famous beginning programmer's error.
As a check, let's verify that we now have 5 NAs in the glucose variable:
``` r
> sum(is.na(pima$glucose))
[1] 5
```
Here the built-in R function **is.na** will return a vector of TRUEs and
FALSEs. Recall that those values can always be treated as 1s and 0s,
thus summable. Thus we got our count, 5.
Let's also check that the mean comes out right:
``` r
> mean(pima$glucose)
[1] NA
```
What went wrong? By default, the **mean** function will *not* skip over
NA values; thus the mean was reported as NA too. But we can instruct
the function to skip the NAs:
``` r
> mean(pima$glucose,na.rm=TRUE)
[1] 121.6868
```
> ❄️ Your Turn
>
> Determine which other columns in **pima** have
> suspicious 0s, and replace them with NA values.
>
> Now, look again at the plot we made earlier of the Nile flow histogram.
> There seems to be a gap between the numbers at the low end and the rest.
> What years did these correspond to? Find the mean of the data,
> excluding these cases.
## Lesson 11: The R List Class
We saw earlier how handy the **tapply** function can be. Let's look at
a related one, **split**. The general call form of the latter is
``` r
split(what to split, what criterion to use for splitting)
```
This looks similar to the form for **tapply** that we saw earlier,
``` r
tapply(what to split, what criterion to use for splitting,
what to do with the resulting grouped data)
```
But this is no surprise, because the internal code for **tapply**
actually calls **split**. (You can check this via **edit(tapply)**; hit
ZZ to exit.)
Earlier we mentioned the built-in dataset **mtcars**, a data frame.
Consider **mtcars$mpg**, the column containing the miles-per-gallon
data. Again, to save typing and avoid clutter in our code, let's make a
copy first:
``` r
> mtmpg <- mtcars$mpg
```
Suppose we wish to split the original vector into three vectors,
one for 4-cylinder cars, one for 6 and one for 8. We *could* do
``` r
> mt4 <- mtmpg[mtcars$cyl == 4]
```
and so on for **mt6** and **mt8**.
> ❄️ Your Turn
>
> In order to keep up, make sure you understand how that
> line of code works, with the TRUEs and FALSEs etc. First print out the
> value of **mtcars$cyl == 4**, and go from there.
But there is a cleaner way:
``` r
> mtl <- split(mtmpg,mtcars$cyl)
> mtl
$`4`
[1] 22.8 24.4 22.8 32.4 30.4 33.9 21.5 27.3 26.0 30.4 21.4
$`6`
[1] 21.0 21.0 21.4 18.1 19.2 17.8 19.7
$`8`
[1] 18.7 14.3 16.4 17.3 15.2 10.4 10.4 14.7 15.5 15.2 13.3 19.2 15.8 15.0
> class(mtl)
[1] "list"
```
In English, the call to **split** said, "Split **mtmpg** into multiple
vectors, with the splitting criterion being the correspond
values in **mtcars$cyl**."
Now **mtl**, an object of R class **"list"**, contains the 3 vectors.
We can access them individually with the dollar sign notation:
``` r
> mtl$`4`
[1] 22.8 24.4 22.8 32.4 30.4 33.9 21.5 27.3 26.0 30.4 21.4
```
Or, we can use indices, though now with double brackets:
``` r
> mtl[[1]]
[1] 22.8 24.4 22.8 32.4 30.4 33.9 21.5 27.3 26.0 30.4 21.4
```
``` r
> mtl[[2]][1:3]
[1] 21.0 21.0 21.4
```
Looking a little closer:
``` r
> head(mtcars$cyl)
[1] 6 6 4 6 8 6
```
We see that the first car had 6 cylinders, so the
first element of **mtmpg**, 21.0, was thrown into the `6` pile, i.e.
**mtl[[2]]** (see above printout of **mtl**), and so on.
And of course we can make copies for later convenience:
``` r
> m4 <- mtl[[1]]
> m6 <- mtl[[2]]
> m8 <- mtl[[3]]
```
Lists are especially good for mixing types together in one package:
``` r
> l <- list(a = c(2,5), b = 'sky')
> l
$a
[1] 2 5
$b
[1] "sky"
```
Note that here we can give names to the list elements, 'a' and 'b'. In
forming **mtl** using **split** above, the names were assigned
according to the values of the vector beiing split. (In that earlier
case, we also needed backquotes `` ``, since the names were numbers.)
If we don't like those default names, we can change them:
``` r
> names(mtl) <- c('four','six','eight')
> mtl
$four
[1] 22.8 24.4 22.8 32.4 30.4 33.9 21.5 27.3 26.0 30.4 21.4
$six
[1] 21.0 21.0 21.4 18.1 19.2 17.8 19.7
$eight
[1] 18.7 14.3 16.4 17.3 15.2 10.4 10.4 14.7 15.5 15.2 13.3 19.2 15.8
15.0
```
What if we want, say, the MPG for the third car in the 6-cylinder
category?
``` r
> mtl[[2]][3]
[1] 21.4
```
The point is that **mtl[[2]]** is a vector, so if we want element 3 of
that vector, we tack on [3].
Or,
``` r
> mtl$six[3]
[1] 21.4
```
By the way, it's no coincidence that a dollar sign is used for
delineation in both data frames and lists; data frames *are* lists.
Each column is one element of the list. So for instance,
``` r
> mtcars[[1]]
[1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
[16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
[31] 15.0 21.4
```
Here we used the double-brackets list notation to get the first element
of the list, which is the first column of the data frame.
> ❄️ Your Turn
>
> In the **mtcars** data, write code to do the following (individually,
> separate code for each):
>
> * Print out the 5th through 8th values for horsepower in 4-cylinder
> cars.
>
> * Print the *last* 3 values in MPG for 6-cylinder cars. This should be
> done fully *programmatically*, i.e. without your setting values by
> had. Make use of the **length** function.
>
> * Find the average horsepower among all cars in the dataset.
>
> * One can divide one vector by another, e.g. c(6,12,25) / c(3,2,5)
> will produce c(2,6,5). Write code that first computes the vector of
> horsepower-to-weight ratios, and then computes their average.
> (Warning: This is *not* the same as average horsepower divided by
> average weight.)
## Lesson 12: Another Look at the Nile Data
Here we'll learn several new concepts, using the **Nile** data as our
starting point.
If you look again at the histogram of the Nile we generated, you'll see
a gap between the lowest numbers and the rest. In what year(s) did
those really low values occur? Let's plot the data against time:
``` r
> plot(Nile)
```
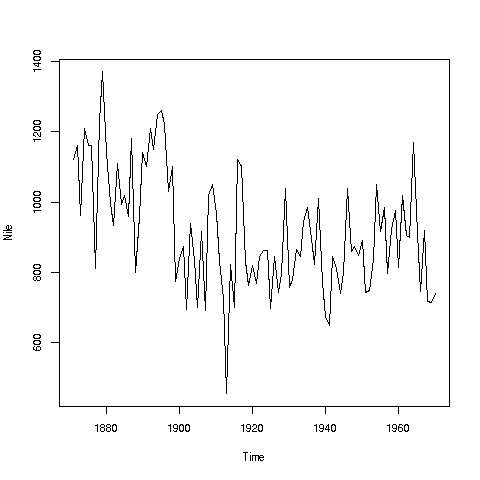
Looks like maybe 1912 or so was much lower than the rest. Is this an
error? Or was there some big historical event then? This would require
more than R to track down, but at least R can tell us which exact year or
years correspond to the unusually low flow. Here is how:
We see from the graph that the unusually low value was below 600. We
can use R's **which** function to see when that occurred:
``` r
> which(Nile < 600)
[1] 43
```
As before, make sure to understand what happened in this code. The
expression **Nile < 600** yields 100 TRUEs and FALSEs. The **which**
then tells us which of those were TRUEs.
So, element 43 is the culprit here, corresponding to year 1871+42=1913.
Again, we would have to find supplementary information in order to
decide whether this is a genuine value or an error, but at least now we
know the exact year.
Of course, since this is a small dataset, we could have just printed out the
entire data and visually scanned it for a low number. But what if the
length of the data vector had been 100,000 instead of 100? Then the
visual approach wouldn't work.
> 📘 Pro Tip
>
> Remember, a goal of programming is to automate tasks, rather
> than doing them by hand.
> ❄️ Your Turn
>
> There appear to be some unusually high values as well,
> e.g. one around 1875. Determine which year this was, using the
> techniques presented here.
>
> Also, try some similar analysis on the
> built-in **AirPassengers** data. Can you guess why those peaks are
> occurring?
>
> Call **hist()** on the **AirPassengers** data, but save the return
> value in a variable **z**. The latter is technically of class
> **histogram**, but is essentially an R list. Type 'str(z)' to see
> what's in it, and write code to find the mean value of the bin counts.
> (Note that this does NOT mean copying the numbers by hand; it should
> be all code.)
Here is another point: That function **plot** is not quite so innocuous
as it may seem. Let's run the same function, **plot**, but with two
arguments instead of one:
``` r
> plot(mtcars$wt,mtcars$mpg)
```
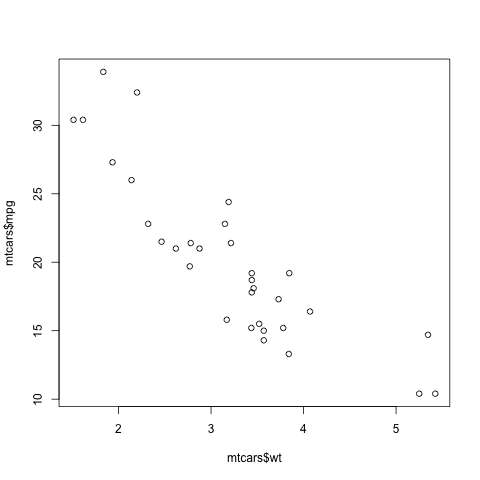
In contrast to the previous plot, in which our data were on the vertical
axis and time was on the horizontal, now we are plotting *two* vectors,
against each other. This enables us to explore the relation between
car weight and gas mileage.
There are a couple of important points here. First, as we might guess,
we see that the heavier cars tended to get poorer gas mileage. But
here's more: That **plot** function is pretty smart!
Why? Well, **plot** knew to take different actions for different input
types. When we fed it a single vector, it plotted those numbers against
time (or, against index). When we fed it two vectors, it knew to do a scatter plot.
In fact, **plot** was even smarter than that. It noticed that **Nile**
is not just of **'numeric'** type, but also of another class, **'ts'**
("time series"):
``` r
> is.numeric(Nile)
[1] TRUE
> class(Nile)
[1] "ts"
```
So, **plot** put years on the horizontal axis, instead of indices 1,2,3,...
And one more thing: Say we wanted to know the flow in the year 1925.
The data start at 1871, so 1925 is 1925 - 1871 = 54 years later. Since
the 1871 number is in element 1 of the vector, that means the flow for
the year 1925 is in element 1+54 = 55.
``` r
> Nile[55]
[1] 698
```
OK, but why did we do this arithmetic ourselves? We should have R do
it:
``` r
> Nile[1 + 1925 - 1871]
[1] 698
```
R did the computation 1925 - 1871 + 1 itself, yielding 55, then looked
up the value of **Nile[55]**. This is the start of your path to
programming -- we try to automate things as much as possible, doing
things by hand as little as possible.
## Lesson 13: Pause to Reflect
> 📘 Pro Tip
>
> Repeating an earlier point:
> How does one build a house? There of course is no set formula. One has
> various tools and materials, and the goal is to put these together in a
> creative way to produce the end result, the house.
>
> It's the same with R. The tools here are the various functions, e.g.
> **mean** and **which**, and the materials are one's data. One then must
> creatively put them together to achieve one's goal, say ferreting out
> patterns in ridership in a public transportation system. Again, it is a
> creative process; there is no formula for anything. But that is what
> makes it fun, like solving a puzzle.
>
> And...we can combine various functions in order to build *our own*
> functions. This will come in future lessons.
## Lesson 14: Introduction to Base R Graphics
One of the greatest things about R is its graphics capabilities. There
are excellent graphics features in base R, and then many contributed
packages, with the best known being **ggplot2** and **lattice**. These
latter two are quite powerful, and will be the subjects of future
lessons, but for now we'll concentrate on the base.
As our example here, we'll use a dataset I compiled on Silicon Valley
programmers and engineers, from the US 2000 census. Let's read
in the data and take a look at the first records:
``` r
> load(url(
'https://github.com/matloff/fasteR/blob/master/data/prgeng.RData?raw=true'))
> head(prgeng)
age educ occ sex wageinc wkswrkd
1 50.30082 13 102 2 75000 52
2 41.10139 9 101 1 12300 20
3 24.67374 9 102 2 15400 52
4 50.19951 11 100 1 0 52
5 51.18112 11 100 2 160 1
6 57.70413 11 100 1 0 0
```
Here we use **load** to input the data, which was stored in R's
compressed form. This function will be explained in [Lesson
16](#less10), but for now, the point is that this was necessary to
preserve the R factor structure of some of the variables.
Here **educ** and **occ** are codes, for levels of education and
different occupations. For now, let's not worry about the specific
codes. (You can find them in the
[Census Bureau document](https://www.census.gov/prod/cen2000/doc/pums.pdf).
For instance, search for "Educational Attainment" for the **educ**
variable.)
Let's start with a scatter plot of wage vs. age:
``` r
> plot(prgeng$age,prgeng$wageinc)
```
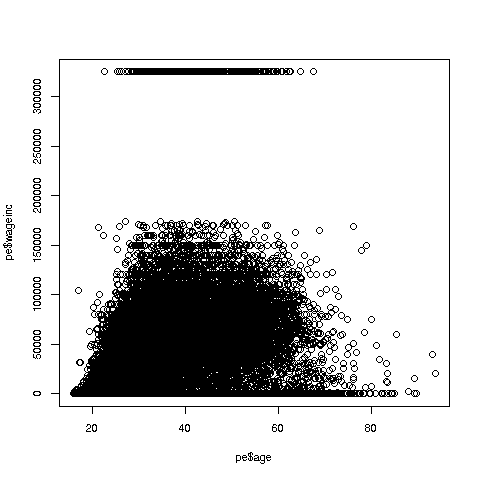
Oh no, the dreaded Black Screen Problem! There are about 20,000 data
points, thus filling certain parts of the screen. So, let's just plot a
random sample, say 2500. (There are other ways of handling the problem,
say with smaller dots or *alpha blending*.)
``` r
> rowNumbers <- sample(1:nrow(prgeng),2500)
> prgeng2500 <- prgeng[rowNumbers,]
```
Recall that the **nrow** function returns the number of rows in the
argument, which in this case is 20090, the number of rows in **prgeng**.
R's **sample** function does what its name implies. Here it randomly
samples 2500 of the numbers from 1 to 20090. We then extracted those
rows of **prgeng**, in a new data frame **prgeng2500**.
> 📘 Pro Tip
>
> Note again that it's usually clearer to break complex operations into
> simpler, smaller ones. I could have written the more compact
>
> ``` r
> > prgeng2500 <- prgeng[sample(1:nrow(prgeng),2500),]
> ```
>
> but it would be hard to read that way. I also use direct function
> composition sparingly, preferring to break
>
> ``` r
> h(g(f(x),3)
> ```
>
> into
>
> ``` r
> y <- f(x)
> z <- g(y,3)
> h(z)
> ```
>
> (As noted earlier, my personal view is that pipes, though also breaking
> complex statements into smaller ones, is less clear and harder to debug,
> so I don't use them.)
So, here is the new plot:
``` r
> plot(prgeng2500$age,prgeng2500$wageinc)
```
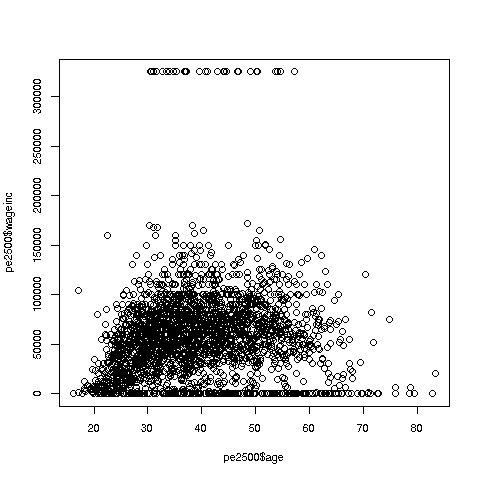
Note that since I plotted a random sample of rows, the ones you get may
differ from the ones I got. The resulting graph will be largely similar
but probably not identical.
OK, now we are in business. A few things worth noting:
* The relation between wage and age is not linear, indeed not even
monotonic. After the early 40s, one's wage tends to decrease. As with
any observational dataset, the underlying factors are complex, but it
does seem there is an age discrimination problem in Silicon Valley.
(And it is well documented in various studies and litigation.)
* Note the horizontal streaks at the very top and very bottom of the
picture. Some people in the census had 0 income (or close to it), as
they were not working. And the census imposed a top wage limit of
$350,000 (probably out of privacy concerns), so that higher numbers were
truncated to that value.
We can break things down by gender, via color coding:
``` r
> plot(prgeng2500$age,prgeng2500$wageinc,col=prgeng2500$sex)
```
The **col** argument indicates we wish to color code, in this case by
gender. It is required to be an R factor.
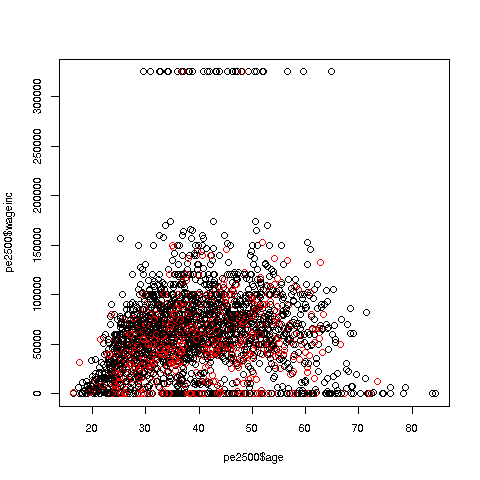
The red dots are the women. (Details below.) Are they generally paid
less than men? There seems to be a hint of that, but detailed
statistical analysis is needed (a future lesson).
It would be good to have better labels on the axes, and maybe smaller
dots:
``` r
> plot(pe2500$age,pe2500$wageinc,col=as.factor(pe2500$sex),
xlab='age',ylab='wage',cex=0.6)
```
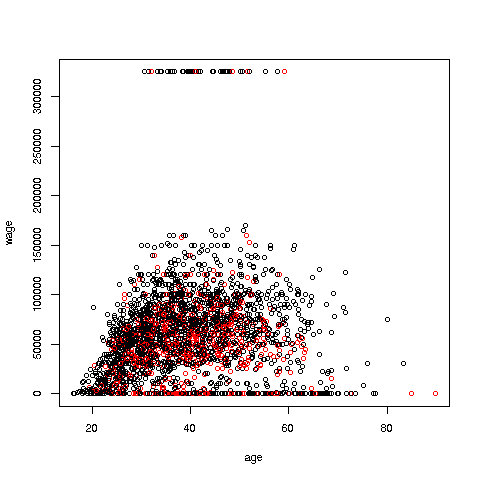
Here 'xlab' meant "X label" and similarly for 'ylab'. The argument 'cex
= 0.6' means "Draw the dots at 60% of default size."
Now, how did the men's dots come out black and the women's red? The men
were coded 1, the women 2. So men got color 1 in the default palette,
black, and the women color 2, red.
There are many, many other features. More in a future lesson.
> ❄️ Your Turn
>
> Use the above data with wage against age again, but this time
> color-coding by education level. (By the way, 1-9 codes no college;
> 10-12 means some college; 13 is a bachelor's degree, 14 a master's, 15 a
> professional degree and 16 is a doctorate.)
## Lesson 15: More on Base Graphics
We can also plot multiple histograms on the same graph. But the
pictures are more effective using a smoothed version of histograms,
available in R's **density** function. Let's compare men's and women's
wages in the census data.
First we use **split** to separate the data by gender:
``` r
> wageByGender <- split(prgeng$wageinc,prgeng$sex)
> dm <- density(wageByGender[[1]])
> dw <- density(wageByGender[[2]])
```
So, **wageByGender[[1]]** will now be the vector of men's wages,
and similarly **wageByGender[[2]]** will have the women's wages.
The **density** function does not automatically draw a plot; it has the
plot information in a return value, which we've assigned to **dm** and
**dw** here. We can now plot the graph:
``` r
> plot(dw,col='red')
> points(dm,cex=0.2)
```
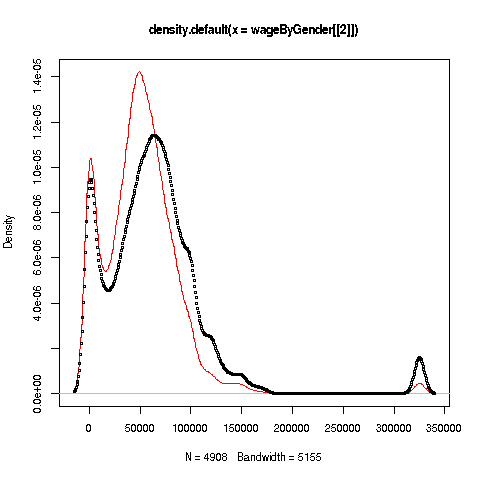
Why did we call the **points** function instead of **plot** in that
second line? The issue is that calling **plot** again would destroy the
first plot; we merely want to *add points* to the existing graph.
And why did we plot the women's data first? As you can see, the women's
curve is taller, so if we plotted the men first, part of the women's
curve would be cut off. Of course, we didn't know that ahead of time,
but graphics often is a matter of trial-and-error to get to the picture
we really want. (In the case of **ggplot2**, the rescaling and
redrawing is done automatically by the software.)
Well, then, what does the graph tell us? The peak for women, occurring
at a little less than $50,000, seems to be at a lower wage than that for
men, at something like $60,000. At salaries around, say, $125,000,
there seem to be more men than women. (Black curve higher than red
curve. Remember, the curves are just smoothed histograms, so, if a
curve is really high at, say 168.0, that means that 168.0 is a very
frequently-occurring value.)
> ❄️ Your Turn
>
> Recall the **prgeng** dataset analyzed earlier. The **occ**
> column has data on six different occupations.
>
> 1. Draw the estimated density curves for **wageinc**, one for each
> occupation, color-coded for the latter..
>
> 2. Draw a scatter plot of **wageinc** versus **age**, one for each
> occupation, color-coded. Thin out the data first, as we did before,
> but now we have six subdatasets, which may require more thinning.
## Lesson 16: Writing Your Own Functions
We've seen a number of R's built-in functions so far, but here comes the
best part -- you can write your *own* functions.
Recall a line we had earlier:
``` r
> sum(Nile > 1200)
```
This gave us the count of the elements in the **Nile** data larger than 1200.
Now, say we want the mean of those elements:
``` r
> gt1200 <- which(Nile > 1200)
> nileSubsetGT1200 <- Nile[gt1200]
> mean(nileSubsetGT1200)
[1] 1250
```
As before, we could instead write a more compact version,
``` r
> mean(Nile[Nile > 1200])
[1] 1250
```
But it's best to do it step by step at first. Let's see how those steps
work. Writing the code with line numbers for reference, the code is
``` r
1 gt1200Indices <- which(Nile > 1200)
2 nileSubsetGT1200 <- Nile[gt1200Indices]
3 mean(nileSubsetGT1200)
```
Let's review how this works:
* In line 1, we find the indices in **Nile** for the elements larger than 1200.
* In line 2, we extract the subset of **Nile** consisting of those
elements.
* In line 3, we compute the desired mean.
But we may wish to do this kind thing often, on many datasets etc. Then
we have:
> 📘 Pro Tip
>
> If we have an operation we will use a lot, we should consider writing a
> function for it.
>
> Say we want to do the above again, but with 1350 instead of 1200. Or,
> with the **tg$len** vector from our ToothGrowth example, with 10.2 as
> our lower bound. We *could* keep typing the same pattern as above,
> but if we're going to do this a lot, it's better to write a function
> for it:
>
> Here is our function:
>
> ``` r
> > mgd <- function(x,d) mean(x[x > d])
> ```
>
> Here I've used a compact form for convenience. (Otherwise I'd
> need to use *blocks* to be covered in a later lesson.) I named it 'mgd'
> for "mean of elements greater than d," but any name is fine.
>
> Let's try it out, then explain:
>
> ``` r
> > mgd(Nile,1200)
> [1] 1250
> > mgd(tg$len,10.2)
> [1] 21.58125
> ```
>
> This saved me typing. In the second call, I would have had to type
>
> ``` r
> mean(tg$len[tg$len > 10.2])
> ```
>
> considerably longer. But even more importantly, I'd have to think about
> the operation each time I used it; by making a function out of it, I've
> got it ready to go, all debugged, whenever I need it.
So, how does all this work? Again, look at the code:
``` r
> mgd <- function(x,d) mean(x[x > d])
> class(mgd)
[1] "function"
```
There is a lot going on here. Bear with me for a moment, as I bring in
a little of the "theory" of R:
Odd to say, but there is a built-in function in R itself named
'function'! We've already seen several built-in R functions, e.g.
**mean**, **sum** and **plot**. Well, here is another,
**function**. We're calling it here. And its job is to build a
function. Yes, as I like to say, to my students' amusement,
> "The function of the function named **function** is to build functions!
> And the class of object returned by **function** is 'function'!"
So, in the line
``` r
> mgd <- function(x,d) mean(x[x > d])
```
we are telling R, "R, I want to write my own function. I'd like to name
it 'mgd'; it will have arguments 'x' and 'd', and it will compute
'mean(x[x > d])', and return that value. Please build the function for
me. Thanks in advance, R!"
Here we called **function** to build and return a 'function' object, and
then assigned that returned object to **mgd**. We can then call the
latter, as we saw above, repeated here for convenience:
``` r
> mgd(Nile,1200)
[1] 1250
```
In executing
``` r
> mgd <- function(x,d) mean(x[x > d])
```
***x*** and ***d*** are known as *formal* arguments, meaning
that they are just placeholders. For example, in
``` r
> mgd(Nile,1200)
```
we said, "R, please execute **mgd** with **Nile** playing the role of
***x***, and 1200 playing the role of ***d***." Here **Nile** and 1200 are
known as the *actual* arguments.
As with variables, we can pretty much name functions and their arguments
as we please.
As you have seen with R's built-in functions, a function will typically
have a return value. In our case here, we could arrange that by writing
``` r
> mgd <- function(x,d) return(mean(x[x > d]))
```
a bit more complicated than the above version. But the call to
**return** is not needed here, because in any function, R will return the
last value computed, in this case the requested mean.
And we can save the function for later use. One way to do this is to
call R's **save** function, which can be used to save any R object:
``` r
> save(mgd,file='mean_greater_than_d')
```
The function has now been saved in the indicated file, which will be in
whatever folder R is running in right now. We can leave R, and say,
come back tomorrow. If we then start R from that same folder, we then
run
``` r
> load('mean_greater_than_d')
```
and then **mgd** will be restored, ready for us to use again.
(Typically this is not the way people save code, but this is
the subject of a later lesson.)
Let's write another function, this one to find the range of a vector,
i.e. the difference between the minimal and maximal values. (Actually,
there is already such a function in R, unsurprisingly named 'range', but
just as an example, let's write our own.)
``` r
> rng <- function(y) max(y) - min(y)
> rng(Nile)
[1] 914
```
Here we made use of the built-in R functions **max** and **min**.
Again, the last item computed in **rng** is the subtraction, so it will
be automatically returned, just what we want. I chose to name the
argument **y**, but it could be anything.
> ❄️ Your Turn
>
> Try your hand at writing some simple functions along
> the lines seen above.
>
> 1. Write a function **cgd()**, like **mgd()** above, but returning the
> count of the number of elements in **x** that are greater than
> **d**.
>
> 2. Write a function **n0(x)**, that returns the number of 0s in the
> vector ***x***. (Hint: Make use of R's **==** and **sum**.)
>
> 3. Write a function **hld(x,d)** that draws a histogram for those
> elements in the vector ***x*** that are less than ***d***.
>
> 4. Write a function **w(x,y)** for vector arguments **x** and **y**
> that outputs a vector of the same length as the inputs, with
> element **i** being the larger of **x[i]** and **y[i]**, except
> that in the case in which those two numbers are equal, the
> corresponding argument in the output vector is 0.
Functions are R objects, just as are vectors, lists and so on. Thus, we
can print them by just typing their names!
``` r
> mgd <- function(x,d) mean(x[x > d])
> mgd
function(x,d) mean(x[x > d])
```
For that matter, we can assign them, e.g.
``` r
> crazynamedfunction <- mgd
> crazynamedfunction(Nile,1200)
[1] 1250
```
Recall that earlier we found that there were several columns in the
Pima dataset that contained values of 0, which were physiologically
impossible. These should be coded NA. We saw how to do that recoding
for the glucose variable:
``` r
> pima$glucose[pima$glucose == 0] <- NA
```
But there are several columns like this, and we'd like to avoid doing
this all repeatedly by hand. (What if there were several *hundred* such
columns?) Instead, we'd like to do this *programmatically*, i.e. purely
by code. This can be done with R's **for** loop construct, which is the
topic of this unit.
> 📘 Pro Tip
>
> Loops are a major workhorse in most programming languages, e.g.
> Python. Most R programmers use them often as well, but oddly some R
> coders believe loops should be used quite sparingly, in situations in
> which a good *functional programming* (FP) alternative is unavailable.
>
> To me, this makes no sense. Loops are easier to code, and very
> important, *easier to debug* than FP code. We will cover FP in Lesson
> 28, but I do not recommend it for R beginners.
>
> I've seen some beginning R coders actually apologize on Twitter for
> using a loop! Write in whatever style you feel comfortable with,
> rather than being a "slave to fashion."
Let's first check which columns seem appropriate for recoding. Recall
that there are 9 columns in this data frame.
``` r
> for (i in 1:9) print(sum(pima[,i] == 0))
[1] 111
[1] 5
[1] 35
[1] 227
[1] 374
[1] 11
[1] 0
[1] 0
[1] 500
```
This is known in the programming world as a *'for' loop*.
The 'print(etc.)' is called the *body* of the loop. The 'for (i in
1:9)' part says, "Execute the body of the loop with i = 1, then execute
it with i = 2, then i = 3, etc. up through i = 9."
In other words, the above code instructs R to do the following:
``` r
i <- 1
print(sum(pima[,i] == 0))
i <- 2
print(sum(pima[,i] == 0))
i <- 3
print(sum(pima[,i] == 0))
i <- 4
print(sum(pima[,i] == 0))
i <- 5
print(sum(pima[,i] == 0))
i <- 6
print(sum(pima[,i] == 0))
i <- 7
print(sum(pima[,i] == 0))
i <- 8
print(sum(pima[,i] == 0))
i <- 9
print(sum(pima[,i] == 0))
```
And this amounts to doing
``` r
print(sum(pima[,1] == 0))
print(sum(pima[,2] == 0))
print(sum(pima[,3] == 0))
print(sum(pima[,4] == 0))
print(sum(pima[,5] == 0))
print(sum(pima[,6] == 0))
print(sum(pima[,7] == 0))
print(sum(pima[,8] == 0))
print(sum(pima[,9] == 0))
```
So, this gives us a report of the number of 0s in each column.
Each run of the loop body is called an *iteration*. We have an
iteration for **i=1**, then one for **i=2** and so on.
Now, it's worth reviewing what those statements do, say the first. Once
again, **pima[,1] == 0** yields a vector of TRUEs and FALSEs, each
indicating whether the corresponding element of column 1 is 0. When we
call **sum**, TRUEs and FALSEs are treated as 1s and 0s, so we get the
total number of TRUEs -- which is a count of the number of elements in that
column that are 0, exactly what we wanted.
The variable **i** in "for (i in 1:9)..." is known as the *index* of the
loop. It's just an ordinary R variable, so name it what you wish.
Instead of **i**, we might name it, say, **colNumber**.
``` r
for (colNumber in 1:9) print(sum(pima[,colNumber] == 0))
```
A technical point: Why did we need the explicit call to **print**?
Didn't we say earlier that just typing an expression at the R '>' prompt
will automatically print out the value of the expression? Ah yes -- but
we are not at the R prompt here! Yes, in the expanded form we see
above,
``` r
print(sum(pima[,1] == 0))
print(sum(pima[,2] == 0))
print(sum(pima[,3] == 0))
print(sum(pima[,4] == 0))
print(sum(pima[,5] == 0))
print(sum(pima[,6] == 0))
print(sum(pima[,7] == 0))
print(sum(pima[,8] == 0))
print(sum(pima[,9] == 0))
```
each command would be issued at the prompt, and **print()** would not be
needed. But in the **for** loop version
``` r
for (i in 1:9) print(sum(pima[,i] == 0))
```
we are calling **print** from *within the loop*, not at the prompt.
So, the explicit call to **print** is needed.
We see in the output of the loop that there are a lot of erroneous 0s in
this dataset, e.g. 35 of them in column 3. We probably have forgotten
which column is which, so let's see, using yet another built-R function:
``` r
> colnames(pima)
[1] "pregnant" "glucose" "diastolic" "triceps" "insulin" "bmi"
[7] "diabetes" "age" "test"
```
Ah, so column 3 was 'diastolic'.
Since some women will indeed have had 0 pregnancies, that column should
not be recoded. And the last column states whether the test for
diabetes came out positive, 1 for yes, 0 for no, so those 0s are
legitimate too.
But 0s in columns 2 through 6 ought to be recoded as NAs. And *the fact
that it's a repetitive action suggests that a **for** loop can be used*
there too:
``` r
> for (i in 2:6) pima[pima[,i] == 0,i] <- NA
```
You'll probably find this line quite challenging, but be patient and, as
with everything in R, you'll find you can master it with patience. Here
goes:
First, let's write it in more easily digestible form:
``` r
> for (i in 2:6) {
+ zeroIndices <- which(pima[,i] == 0)
+ pima[zeroIndices,i] <- NA
+ }
```
You can enter the code for a loop or function etc. line by line at the
prompt, as we've done here. R helpfully uses its '+' prompt (which I
did *not* type) to remind me that I am still in the midst of typing the
code. (After the '}' I simply hit Enter to tell R that I'm done.)
Here I intended the body of the loop to consist of a *block* of two
statements, not one, so I needed to tell R that, by enclosing them with
'{' and '}.
Entering code line-by-line as above, is a quick and convenient way to
create a short loop or function. But generally, we use a text editor,
either standalone as with the famous Vim, or as part of an IDE like
RStudio. But for now, we'll work as above.
For your convenience, below is the code itself, no '+' symbols. You can
copy-and-paste into R, with the result as above.
```
for (i in 2:6) {
zeroIndices <- which(pima[,i] == 0)
pima[zeroIndices,i] <- NA
}
```
So, the block (two lines here) will be executed with **i** = 2, then 3,
4, 5 and 6. The line
``` r
zeroIndices <- which(pima[,i] == 0)
```
determines where the 0s are in column **i**, and then the line
``` r
pima[zeroIndices,i] <- NA
```
replaces those 0s by NAs.
> 📘 Pro Tip
>
> Note that I have indented the two lines in the block. This is not
> required but is considered good for clear code, in order to easily
> spot the block when you or others read the code.
Sometimes our code needs to leave a loop early, which we can do using
the R **break** construct. Say we are adding cubes of numbers
1,2,3,..., and for some reason want to determine which sum--if any-- is
the first to exceed **s**:
``` r
> f
function(n,s)
{
tot <- 0
for (i in 1:n) {
tot <- tot + i^3
if (tot > s) {
print(i)
break
}
if (i == n) print('failed')
}
}
> f(100,345)
[1] 6
> f(5,345)
[1] "failed"
```
Here our creation of the function **f()** is not shown, but note what we
did after creating it--we typed its name at the R prompt, and sure
enough, it printed out! Functions are objects, and R has been designed
so that these objects can be printed.
Let's see what the code does; there is quite a bit there.
First, note the **if** statement. If the current total is greater than
**s**, we execute the block that follows it (the **print** and
**break**), so that we print out the value of **i** that had put us over
the top and then leave the loop by executing the **break**. And since
there is no code in this function following the loop, we exit the
function.
On the other hand, if the current total is not greater than **s**
we skip that block, and go to the next statement. That latter turns out
to be another **if**. It checks
A better approach is to use 'while' loops, covered later in this
tutorial.
## Lesson 18: Functions with Blocks
Blocks are usually key in defining functions. Let's generalize the
above code in the Loops lesson, writing a function that replaces 0s by
NAs in specified columns in general data frames, not just **pima** as
before.
``` r
1 zerosToNAs <- function(d,cols)
2 {
3 for (j in cols) {
4 NArows <- which(d[,j] == 0)
5 d[NArows,j] <- NA
6 }
7 d
8 }
```
(We've added line numbers to this display for convenence.)
Here the formal argument **d** is the data frame to be worked on, and
**cols** specifies the columns in which 0s are to be replaced.
The loop goes through **d**, one column at a time. Since **d[,j]**
means all of column **j** of **d**, then **which(d[,j] == 0)** will give
us the indices in that column of elements that are 0s. Those indices in
turn are row numbers in **d**. In other words, **NArows** is a vector
cntaining the row numbers of the 0s in column **j**. In line 5, then,
we replace the 0s we've found in column **j** by NAs. Before
continuing, work through this little example in your mind:
``` r
> d <- data.frame(x=c(1,0,3),y=c(0,0,13))
> d
x y
1 1 0
2 0 0
3 3 13
> which(d[,2] == 0)
[1] 1 2 # ah yes; the 0 elements in column 2 are at indices 1 and 2
```
Returning to the above loop code, note that when we reach line 7, we've
already finished the loop, and exited from it. So, we are ready to
return the new value of **d**. Recall that we could do this via the
expression **return(d)**, but we can save ourselves some typing by
simply writing 'd'. That value becomes the last value computed, and R
automatically returns that last value.
We could use this in the Pima data:
``` r
> pima <- zerosToNAs(pima,2:6)
```
There is an important subtlety here. All of this will produce a new
data frame, rather than changing **pima** itself. That does look odd;
isn't **d** changing, and isn't **d** the same as **pima**? Well, no;
**d** is only a *separate copy* of **pima**. So, when **d** changes,
**pima** does not. So, if we want **pima** to change, we must reassign
the output of the function back to **pima**, as we did above.
> ❄️ Your Turn
>
> Write a function with call form **countNAs(dfr)**,
> which prints the numbers of NAs in each column of the data frame
> **dfr**. You'll need to use the built-in **is.na** functon; execute
> **is.na(c(5,NA,13,28,NA))** at the R command prompt to see what it
> does. Test it on a small artificial dataset that you create.
## Lesson 19: Text Editing and IDEs
In trying out our function **zeroToNAs** above, you probably used your
computer's mouse to copy-and-paste from this tutorial into your machine.
Your screen would then look like this:
```
> zerosToNAs <- function(d,cols)
+ {
+ zeroIndices <- which(d[,cols] == 0)
+ d[zeroIndices,cols] <- NA
+ d
+ }
```
But this is unwieldy. Typing it in line by line is laborious and
error-prone. And what if we were to change the code? Must we type in
the whole thing again? We really need a *text editor* for this. Just
as we edit, say, reports, we do the same for code.
Here are your choices:
1. If you are already using an IDE, say RStudio, you simply edit
in the designated pane.
2. If you are using an external editor, say vim or emacs,
just open a new file and use that workspace.
3. For those not using these, we'll just use R's built-in **edit**
function.
Option 3 is fine for now, but eventually you'll want to use either
Option 1 or 2. You may wish to start with one of those options now,
before going further.
We have details on getting start with RStudio in the Appendix at the end of this document. **Warning:**
As noted earlier, one major R Users Group described RStudio as
"overwhelming." But it is quite easy if you resist the temptation (or
the exhortations of others) to learn it all at once. As long as you
stick to the basics in the Appendix, you'll find it quite easy; you can
learn the advanced tricks later.
Consider the following toy example:
``` r
f <- function(x,y)
{
s <- x + y
d <- x - y
c(s,d)
}
```
It finds the sum and difference of the inputs, and returns them as a
two-element vector.
If you are using RStudio or an external editor, copy-and-paste the above
code into the workspace of an empty file.
Or, to create **f** using **edit**, we would do the following:
``` r
> f <- edit()
```
This would invoke the text editor, which will depend on your machine.
It will open your text editor right there in your R window. Type the
function code, then save it, using the editor's Save command.
**IMPORTANT:** Even if you are not using **edit**, it's important to
know what is happening in that command above.
a. **edit** itself is a function. Its return value is the code you
typed in!
b. That code is then assigned to **f**, which you can now call
If you want to change the function, in the RStudio/external editor case,
just edit it there. In the **edit** case, type
``` r
> f <- edit(f)
```
This again opens the text editor, but this time with the current **f**
code showing. You edit the code as desired, then as before, the result
is reassigned to **f**.
How do you then run the code, say for computing **f(5,2)**?
* If you had created **f** using **edit**, then execute as usual:
``` r
> f(5,2)
```
* If you had used an external text editor, say saving the code into the
file **a.R**, then
``` r
> source('a.R')
```
loads file, and then you run as above.
* In RStudio, click on Source, then run as above.
## Lesson 20: If, Else, Ifelse
In our Census data example above, it was stated that education codes 0-9
all corresponded to having no college education at all. For instance, 9
means high school graduate, while 6 means schooling through the 10th
grade. (Of course, few if any programmers and engineers have
educational attainment level below college, but this dataset was
extracted from the general data.) 13 means a bachelor's degree.
Suppose we wish to color-code the wage-age graph in an earlier lesson by
educational attainment. Let's amalgamate all codes under 13, giving them
the code 12.
The straightforward but overly complicated, potentially slower way would
be this:
``` r
> head(pe$educ,15)
[1] 13 9 9 11 11 11 12 11 14 9 12 13 12 13 6
> for (i in 1:nrow(pe)) {
+ if (pe$educ[i] < 13) pe$educ[i] <- 12
+ }
> head(pe$educ,15)
[1] 13 12 12 12 12 12 12 12 14 12 12 13 12 13 12
```
For pedagogical clarity, I've inserted "before and after" code, using
**head**, to show the **educ** did indeed change where it should.
The **if** statement works pretty much like the word "if" in English.
First **i** will be set to 1 in the loop, so R will test whether
**pe$educ[1]** is less than 13. If so, it will reset that element to
12; otherwise, do nothing. Then it will do the same for **i** equal to
2, and so on. You can see above that, for instance, **pe$educ[2]** did
indeed change from 9 to 12.
But there is a slicker (and actually more standard) way to do this
(re-read the data file before running this, so as to be sure the code
worked):
``` r
> edu <- pe$educ
> pe$educ <- ifelse(edu < 13,12,edu)
```
(Once again, we've broken what could have been one line into two, for
clarity.)
Now how did that work? As you see above, R's **ifelse** function
has three arguments, and its return value is a new vector, that in this
case we've reassigned to **pe$educ**. Here, **edu < 12** produces a vector
of TRUEs and FALSEs. For each TRUE, we set the corresponding element of
the output to 12; for each FALSE, we set the corresponding element of
the output to the corresponding element of **edu**. That's exactly what
we want to happen.
So, we can now produce the desired graph:
``` r
> plot(pe$age,pe$wageinc,col=edu)
```
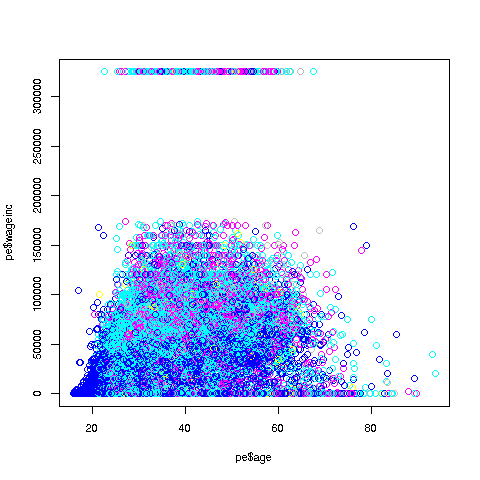
By the way, an ordinary **if** can be paired with **else** too. For
example, say we need to set **y** to either -1 or 1, depending on
whether **x** is less than 3. We could write
``` r
if (x < 3) y <- -1 else y <- 1
```
One more important point: Using **ifelse** instead of a loop in the
above example is termed *vectorization*. The name comes from the fact
that **ifelse** operates on vectors, while in the loop we operate on one
individual element at a time.
Vectorized code is typically much more compact than loop-based code, as
was the case here. In some cases, though certainly not all, the
vectorized version will be much faster.
By the way, note the remark above, "**ifelse** operates on vectors."
Let's revisit the above statement with this point in mind.
``` r
> pe$educ <- ifelse(edu < 13,12,edu)
```
It would be helpful to keep in mind that both the 13 and the 12 will be
recycled, as expained before. The **edu** vector is 20090 elements
long, so in order to be compared on an element-to-element basis, the 13
has to be recycled to a vector consisting of 20090 elements that are
each 13. The same holds for the 12.
Here's another example. Say we wish to recode the **Nile** data to a
new vector **nile**, with values 1, 2 and 3, for the cases in which the
value is less than 800, between 800 and 1150 inclusive, or greater than
1150. We could do this:
``` r
> nile <- ifelse(Nile > 1150,3,2)
> nile <- ifelse(Nile < 800,1,nile)
# check it
> table(nile)
nile
1 2 3
26 62 12
```
After the first call to **ifelse**, the vector **nile** (not **Nile**;
variable names etc. are case-sensitive) consists of 2s and 3s. The 3s
are right, but the 2s need further work, hence the second call.
But let's look closely at the second call, to review some things we've
seen before:
1. The expression **Nile > 1150** evaluates to a vector of 100 TRUEs and
FALSEs.
2. The singleton value 800 is then recycled to one hundred
800s, to set up the '<'. Let's call the result of that '<' operation w.
3. Then **ifelse(Nile < 800,1,nile)** says, "For each element in the vector
w that is TRUE, write down a 1; for each element that is FALSE, write
down whatever the corresponding value is in **nile**."
Well, congratulations! With **for** and now **ifelse**, you've really
gotten into the programming business. We'll be using them a lot in the
coming lessons.
> ❄️ Your Turn
>
> Write a **for** loop version of the **Nile** example
> above.
## Lesson 21: Do Professional Athletes Keep Fit?
Many people gain weight as they age. But what about professional
athletes? They are supposed to keep fit, after all. Let's explore this
using data on professional baseball players. (Dataset courtesy of the
UCLA Statistics Dept.)
``` r
> load(url('https://github.com/matloff/fasteR/blob/master/data/mlb.RData?raw=true'))
> head(mlb)
Name Team Position Height Weight Age PosCategory
1 Adam_Donachie BAL Catcher 74 180 22.99 Catcher
2 Paul_Bako BAL Catcher 74 215 34.69 Catcher
3 Ramon_Hernandez BAL Catcher 72 210 30.78 Catcher
4 Kevin_Millar BAL First_Baseman 72 210 35.43 Infielder
5 Chris_Gomez BAL First_Baseman 73 188 35.71 Infielder
6 Brian_Roberts BAL Second_Baseman 69 176 29.39 Infielder
> class(mlb$Height)
[1] "integer"
> class(mlb$Name)
[1] "factor"
```
(As usual, after reading in the data, we took a look around, glancing at
the first few records, and looking at a couple of data types.)
Now, as a first try in assessing the question of weight gain over time,
let's look at the mean weight for each age group. In order to have
groups, we'll round the ages to the nearest integer first, using the R
function, **round**, so that e.g. 21.8 becomes 22 and 35.1 becomes 35.
Let's explore the data using R's **table** function.
``` r
> age <- round(mlb$Age)
> table(age)
age
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
2 20 58 80 103 104 106 84 80 74 70 44 44 32 32 22 20 12 6 7
41 42 43 44 49
9 2 2 1 1
```
Not surprisingly, there are few players of extreme age -- e.g. only two of
age 21 and one of age 49. So we don't have a good sampling at those age
levels, and may wish to exclude them (which we will do shortly).
Now, how do we find group means? It's a perfect job for the **tapply**
function, in the same way we used it before:
``` r
> taout <- tapply(mlb$Weight,age,mean)
> taout
21 22 23 24 25 26 27 28
215.0000 192.8500 196.2241 194.4500 200.2427 200.4327 199.2925 203.9643
29 30 31 32 33 34 35 36
199.4875 204.1757 202.8429 206.7500 203.5909 204.8750 209.6250 205.6364
37 38 39 40 41 42 43 44
203.2000 200.6667 208.3333 207.8571 205.2222 230.5000 229.5000 175.0000
49
188.0000
```
To review: The call to **tapply** instructed R to split the
**mlb$Weight** vector according to the corresponding elements in the
**age** vector, and then find the mean in each resulting group. This
gives us exactly what we want, the mean weight in each age group.
So, do we see a time trend above? Again, we should dismiss the extreme
low and high ages, and we cannot expect a fully consistent upward trend over
time, because each mean value is subject to sampling variation. (We
view the data as a sample from the population of all professional
baseball players, past, present and future.) That said, it does seem
there is a slight upward trend; older players tend to be heavier!
By the way, note that **taout** is vector, but with additional
information, in that the elements have names, in this case the ages. In
fact, we can extract the names into its own vector if needed:
``` r
> names(taout)
[1] "21" "22" "23" "24" "25" "26" "27" "28" "29" "30" "31" "32" "33"
"34" "35"
[16] "36" "37" "38" "39" "40" "41" "42" "43" "44" "49"
```
Let's plot the means against age. We'll just plot the means that are
based on larger amounts of data. So we'll restrict it to, say, ages 23
through 35, all of whose means were based on at least 30 players. That
age range corresponded to elements 3 through 15 of **taout**, so here is
the code for plotting:
``` r
> plot(23:35,taout[3:15])
```
There does indeed seem to be an upward trend in time. Ballplayers
should be more careful!
(Though it is far beyond the scope of this tutorial, which is on R
rather than statistics, it should be pointed out that interpretation of
the regression coefficients must be done with care. It may be, for
instance, that heavier players tend to have longer careers. If so,
fitting our linear form to data that has many older, heavier players may
misleadingly imply that most individual players gain weight as they age.
And of course, they would insist the gained weight
is all muscle. :-) )
Note again that the **plot** function noticed that we supplied it with
two arguments instead of one, and thus drew a two-dimensional scatter
plot. For instance, in **taout** we see that for age group 25, the mean
weight was 200.2427, so there is a dot in the graph for the point
(25,200.2427).
> ❄️ Your Turn
>
> There are lots of little experiments you can do on this
> dataset. For instance, use **tapply** to find the mean weight for
> each position; is the stereotype of the "beefy" catcher accurate, i.e.
> is the mean weight for that position higher than for the others?
> Another suggestion: Plot the number of players at each age group, to
> visualize the ages at which the bulk of the players fall.
## Lesson 22: Linear Regression Analysis, I
Looking at the picture in the last lesson, it seems we could draw a
straight line through that cloud of points that fits the points pretty
well. Here is where linear regression analysis comes in.
We of course cannot go into the details of statistical methodology here,
but it will be helpful to at least get a good definition set:
> As mentioned, we treat the data as a sample from the (conceptual)
> population of all players, past, present and future. Accordingly,
> there is a population mean weight for each age group. It is assumed
> that those population means, when plotted against age, lie on some
> straight line.
In other words, our model is
mean weight = β0 + β1 height
where β0 and β1 are the
intercept and slope of the population regression line.
So, we need to use the data to estimate the slope and intercept of that
straight line, which R's **lm** ("linear model") function does for us.
We'll use the original dataset, since the one with rounded ages was just
to guide our intuition.
``` r
> lm(Weight ~ Age,data=mlb)
Call:
lm(formula = Weight ~ Age, data = mlb)
Coefficients:
(Intercept) Age
181.4366 0.6936
```
Here the call instructed R to estimate the regression line of weight
against age, based on the **mlb** data.
So the estimated slope and intercept are 0.6936 and 181.4366,
respectively. (Remember, these are just sample estimates. We don't
know the population values.) R has a provision by which we can draw the
line, superimposed on our scatter plot:
``` r
> abline(181.4366,0.6936)
```
> ❄️ Your Turn
>
> In the **mtcars** data, fit a linear model of the
> regression of MPG against weight; what is the estimated
> effect of 100 pounds of extra weight?
> 📘 Pro Tip
>
> Remember, the point of computers is to alleviate us of work. We should
> avoid doing what the computer could do. For instance,
> consider the graph in the last lesson: We had typed
>
> ``` r
> > abline(181.4366,0.6936)
> ```
>
> but we really shouldn't have to type those numbers in by hand -- and we
> don't have to. Here's why:
As mentioned earlier, R is an *object-oriented language*. Everthing is
an *object*, and every object has a *class*. One of the most common
class structures is called 'S3'.
When we call **lm**, the latter returns an S3 object of 'lm' class:
``` r
> lmout <- lm(Weight ~ Age,data=mlb)
> class(lmout)
[1] "lm"
```
A handy way to take a quick glance at the contents of an object is
via the **str** function:
``` r
> str(lmout)
List of 12
$ coefficients : Named num [1:2] 181.437 0.694
..- attr(*, "names")= chr [1:2] "(Intercept)" "Age"
...
...
- attr(*, "class")= chr "lm"
```
Our use of ... here is to indicate that we've omitted a lot of the
output. But a couple of things stand out even in this excerpt:
1. Our **lmout** object here is an R list (which is the nature of S3
objects). That R list here has 12 elements.
2. But it has an extra *attribute*, which is the class name, in this
case **'lm'**. (So the designers of R simply chose to name the class
after the function, which is not always the case.)
3. The first of the elements of this R list is named 'coefficients', and it
is a vector containing the slope and intercept.
So, we don't have to type the slope and intercept in by hand after all.
``` r
> cfs <- lmout$coefficients
> abline(a = cfs[1], b = cfs[2])
```
By the way, **abline** is actually a *generic* function, like **print**
and **plot**. That is, it works on various kinds of object classes.
One such class is 'lm'! So if we want to be clever, we can add our line
to the graph using this approach:
``` r
> abline(lmout)
```
The internal code for **abline** recognizes that **lmout** is of 'lm'
class, and thus knows it can find the coefficients in the **coefficients**
element of the **lmout** list. Saves us a lot of work!
Now, what about our original question -- do baseball players gain weight
as they age? The answer appears to be yes; for each additional year of
age, the estimated mean age increases by about 0.7 pound. That's about
7 pounds in 10 years, rather remarkable.
Again, this is only an estimate -- 181.437 and 0.694 are estimates of
the unknown population values β0 and β1.
-- generated from sample data. We can get an idea of the accuracy of
this estimate by calculating a *confidence interval*, but we'll leave
that for statistics courses.
But we can do more right now. One might ask, Shouldn't we also account
for a player's height, not just his age? After all, taller people tend
to be heavier. Yes, we should do this:
``` r
> lmo <- lm(Weight ~ Height + Age, data=mlb)
> lmo
Call:
lm(formula = Weight ~ Height + Age, data = mlb)
Coefficients:
(Intercept) Height Age
-187.6382 4.9236 0.9115
```
Here we instruct R to find the estimated regression function of weight,
using both height and age as predictors. The '+' doesn't mean addition; it
is simply a delimiter between the predictors height and age in our regression
specification.
So the new model is
mean weight = β0 + β1 height + β2 age
This says:
estimated mean weight = -187.6382 + 4.9236 height + 0.9115 age
So, under this more refined analysis, things are even more pessimistic;
players on average gain about 0.9 pounds per year. And by the way, an
extra inch of height corresponds on average to about 4.9 pounds of extra
weight; taller players are indeed heavier, as we surmized.
Warning:
Though this is not a statistics tutorial *per se*, an important point
should be noted. Regression analysis has two goals, Description and
Prediction. Our above analysis was aimed at the former -- we want to
*describe* the nature of fitness issues in pro baseball players. As we
saw, a coefficient can change quite a lot when another predictor is
added to the model, and in fact can even change sign ("Simpson's
Paradox"). Suppose for instance the shorter players tend to have longer
careers. If we do *not* include height in our model, that omission
might bias the age coefficient downward. Thus great care must be taken
in interpreting coefficients in the Description setting. For
Prediction, it is not as much of an issue.
> ❄️ Your Turn
>
> In the **mtcars** data, fit a linear model of the
> regression of MPG against weight and horsepower; what is the estimated
> effect of 100 pounds of extra weight, for fixed horsepower?
## Lesson 24: Baseball Player Analysis (cont'd.)
This lesson will be a little longer and more detail-oriented. But it
will give you more practice on a number of earlier topics, and will also
bring in some new R functions for you. Spending extra time on
this lesson will pay substantial dividends.
We might wonder whether the regression lines differ much among player
positions. (A more statistical approach would be to include
*interaction terms* in the model.) Let's first see what positions are
tabulated:
``` r
> table(mlb$PosCategory)
Catcher Infielder Outfielder Pitcher
76 210 194 535
```
Let's fit the regression lines separately for each position type.
There are various ways to do this, involving avoidance of loops to
various degrees. But we'll keep it simple, which will be clearer.
First, let's split the data by position. You might at first think this
is easily done using the **split** function, but that doesn't work,
since that function is for splitting vectors. Here we wish to split a
data frame.
So what can be done instead? We need to think creatively here. One
solution is this:
We need to determine the row numbers of the catchers, the row numbers of
the infielders and so on. So we can take all the row numbers,
**1:nrow(mlb)**, and apply **split** to that vector!
``` r
> rownums <- split(1:nrow(mlb),mlb$PosCategory)
```
There are 1015 rows in **mlb**, so this says, "Take the row numbers
1:1015, and split them according to the **PosCategory** column of **mlb**."
The resulting piles of row numbers will be the row numbers for catchers,
then the row numbers for infielders and so on.
As usual, following an intricate operation like this, we should glance
at the result:
``` r
> str(rownums)
List of 4
$ Catcher : int [1:76] 1 2 3 35 36 66 67 68 101 102 ...
$ Infielder : int [1:210] 4 5 6 7 8 9 37 38 39 40 ...
$ Outfielder: int [1:194] 10 11 12 13 14 15 16 43 44 45 ...
$ Pitcher : int [1:535] 17 18 19 20 21 22 23 24 25 26 ...
```
So the output is an R list; no surprise there, as we knew beforehand
that **split** produces an R list. Also not surprisingly, the elements
of the list are named "Catcher" etc. So for example, the third
outfielder is in row 12 of the data frame.
> 📘 Pro Tip
>
> The idea here, using **split** on **1:nrow(mlb)**, was a bit of a trick.
> Actually, it is a common ploy for experienced R coders, but you might
> ask, "How could a novice come up with this idea?"
>
> The answer, as noted several times already here, is that programming
> is a creative process. This was a creative solution.
>
> Creativity may not come quickly! Of course, there are many forums on
> the Web at which you can ask questions, e.g. Stack Overflow, but
> *resist the temptation to immediately go that route*. Don't give up!
> The more you think about a problem, the more skilled you will get,
> even if you sometimes come up empty-handed.
Now, remember, a nice thing about R lists is that we can reference their
elements in various ways. The first element above, for instance, is any
of **rownums$Catcher**, **rownums[['Catcher']]** and **rownums[[1]]**,
This versatility is great, as for example we can use the latter two
forms to write loops.
And a loop is exactly what we need here. (One can also do this with
*functional programming*, which we will cover in a later lesson.) We
want to call **lm** four times, once for each position. We could do
this, say, with a loop beginning with
``` r
for (i in 1:4)
```
to iterate through the four position types, but it will be clearer if we
use the names:
``` r
for (pos in c('Catcher','Infielder','Outfielder','Pitcher'))
```
Recall 'for' loops are of the form
``` r
for (variable in vector)...
```
Instead of having a numeric vector, e.g. the 1:4 above, we now have a
character vector, which each element of the vector being a character
string, i.e. 'Catcher', 'Infielder' etc., but the principles are the same.
We could have **lm** and **print** calls in the body of the loop.
But let's be a little fancier, building up a data frame with the output.
We'll start with an empty frame, and keep adding rows to it.
Our code is
``` r
posNames <- c('Catcher','Infielder','Outfielder','Pitcher')
m <- data.frame()
for (pos in posNames) {
posRows <- rownums[[pos]]
lmo <- lm(Weight ~ Age, data = mlb[posRows,])
newrow <- lmo$coefficients
m <- rbind(m,newrow)
}
```
Here is the output:
``` r
> m
X180.828029016113 X0.794925225995348
1 180.8280 0.7949252
2 170.2466 0.8589593
3 176.2884 0.7883343
4 185.5994 0.6543904
```
Some key things to note here.
* The overall strategy is to start with an empty data frame, then keep
adding rows to it, one row of regression coefficients per player position.
* In order to add rows to **m**, we used R's **rbind** ("row bind")
function. The expression **rbind(m,newrow)** forms a new data frame,
by tacking **newrow** onto **m** and returning the result. Here we
reassign the result back to **m**, also a common operation. (Note
carefully: The **rbind** operation did not change **m**; it merely
created a new data frame. To update **m**, we needed to assign that
new data frame to **m**.) By the way, there is also a **cbind**
function for columns.
* In the call to **lm**, we used **mlb[rownums[[pos]],]** instead of
**mlb** as previously, since here we wanted to fit a regression line
on each position subgroup. So, we restricted attention to only those
rows of **mlb** for which the position was equal to the current value
of **pos**.
So, what happens is: **m** is initially an empty data frame. Then the
loop, for its first iteration, sets **pos** to 'Catcher'. Then a
regression line will be fit to the rows of **mlb** that are for
catchers. That fit is returned to us from **lm**, and we extract the
coefficients, assigning them to **lmo**. (Once again, the name is
arbitrary; I chose this one to symbolize "lm output.") We extract the
coefficients and tack them on at the end of **m**.
> 📘 Pro Tip
>
> This is a very common *design
> pattern* in R (and most other languages), to build up a data frame (or
> similar structure) row by row in a loop.
Nice output, with the two columns aligned. But those column names are
awful, and the row labels should be nicer than 1,2,3,4. We can fix
these things:
``` r
> row.names(m) <- posNames
> names(m) <- c('intercept','slope')
> m
intercept slope
Catcher 180.8280 0.7949252
Infielder 170.2466 0.8589593
Outfielder 176.2884 0.7883343
Pitcher 185.5994 0.6543904
```
What happened here? We earlier saw the built-in **row.names** function,
so that setting row names was easy. But what about the column names?
Recall that a data frame is actually an R list, consisting of several
vectors of the same length, which form the columns. So, **names(m)** is
the names of the columns.
So with a little finessing here, we got some nicely-formatted output.
Moreover, we now have our results in a data frame for further use. For
instance, we may wish to plot the four lines on the same graph, and we
would use rows of the data frame as input.
A little more finessing is possible. Look at the line
``` r
posNames <- c('Catcher','Infielder','Outfielder','Pitcher')
```
We're using a computer! We shouldn't have to type out these names by
hand, as I did in this line. In fact, we already have them in one of
our R objects, **rownums**; recall our earlier check:
``` r
> str(rownums)
List of 4
$ Catcher : int [1:76] 1 2 3 35 36 66 67 68 101 102 ...
$ Infielder : int [1:210] 4 5 6 7 8 9 37 38 39 40 ...
$ Outfielder: int [1:194] 10 11 12 13 14 15 16 43 44 45 ...
$ Pitcher : int [1:535] 17 18 19 20 21 22 23 24 25 26 ...
```
The elements of the R list **rownums** are the names of the positions!
So, the better way to set **posNames** is
``` r
posNames <- names(rownums)
```
> 📘 Pro Tip
>
> Again, the reader may be thinking,
> "How in the world would I have been able to realize this?" Again, the
> answer is that as you acquire more experience in coding, you will be
> more and more able to come up with creative insights like this. Patience!
Finally, what about those numerical results? There is substantial
variation in those estimated slopes, but again, they are only estimates.
The question of whether there is substantial variation at the population
level is one of statistical inference, to be discussed in a later
lesson.
## Lesson 25: R Packages, CRAN, Etc.
One of the great things about R is that are tens of thousands of
packages that were developed by users and then contributed to
the [CRAN repository](https://cran.r-project.org). As of December 2020,
there were nearly 17,000 packages there. If you need to do some special
operation in R, say spatial data analysis, it may well be in there.
You might take the [CRAN Task Views](https://cran.r-project.org/web/views/)
as your starting point, or simply use Google, e.g. plugging in the search
term "CRAN spatial data."
Other good sources of public R packages are
[Bioconductor](https://www.bioconductor.org/) and useRs' personal GitHub
pages.
Below, we'll introduce one of the most popular user-contributed
packages, **ggplot2**. But first, how does one install and load
packages?
First, one needs a place to put the packages. UseRs often designate a
special folder/directory for their packages (both those they download
and ones they write themselves). I use 'R' in my home directory for
that purpose, but if you don't specify a folder, your package installer
will choose one for you. It won't matter as long as you are consistent.
I'll assume you don't specify a package folder.
To install, say, **ggplot2**, you can type at the R prompt,
``` r
> install.packages('ggplot2')
```
Or in RStudio, choose Tools | Install Packages...
When you want to use one of your installed packages, you need to tell R
to load it, e.g. by typing at the R prompt,
``` r
> library(ggplot2)
```
In RStudio, click the Packages button and select the one you want; there
may be a delay while R makes a list of all your packages.
Later, you'll write your own R packages. We won't cover that here, but
there are many good tutorials for this on the Web.
## Lesson 26: A Pause, Before Going on to Advanced Topics
At this point, you have a pretty good grounding in R. You are capable
of doing lots of things in R. It may be all you need, but even if not,
you know enough to ask a question online if you get stuck on something.
The remaining topics are more advanced, and lessons will be somewhat
longer and more detailed that the previous ones. But you are still
strongly encouraged to go through them, as they will not only cover new
topics but also give you deeper insight into the earlier material.
## Lesson 27: The ggplot2 Graphics Package
Now, on to **ggplot2**.
The **ggplot2** package was written by Hadley Wickham, who later became
Chief Scientist at RStudio. It's highly complex, with well over 400
functions, and rather abstract, but quite powerful. We will touch on it
at various points in this tutorial, while staying with base-R graphics
when it is easier to go that route.
Now to build up to using **ggplot2**, let's do a bit more with base-R
graphics first, continuing with our weight/age investigation of the
ballplayers. To begin, let's do a scatter plot of weight against age,
color-coded by position. We could type
``` r
> plot(mlb$Age,mlb$Weight,col=mlb$PosCategory)
```
but to save some typing, let's use R's **with** function (we'll change
the point size while we are at it):
``` r
> with(mlb,plot(Age,Weight,col=PosCategory,cex=0.6))
```
By writing **with**, we tell R to take Age, Weight and PosCategory in
the context of **mlb**.
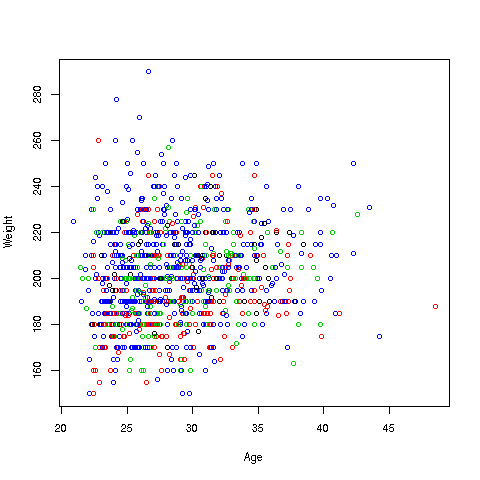
Here is how we can do it in **ggplot2**:
First, I make an empty plot, based on the data frame **mlb**:
``` r
> p <- ggplot(mlb)
```
Nothing will appear on the screen. The package displays only when you
"print" the plot:
``` r
> p
```
This will just display an empty plot. (Try it.) By the way, recall
that any expression you type, even 1 + 1, will be evaluated and printed
to the screen. Here the plot (albeit) empty is printed to the screen.
Now let's do something useful:
``` r
> p + geom_point(aes(x = Age, y = Weight, col = PosCategory),cex=0.6)
```
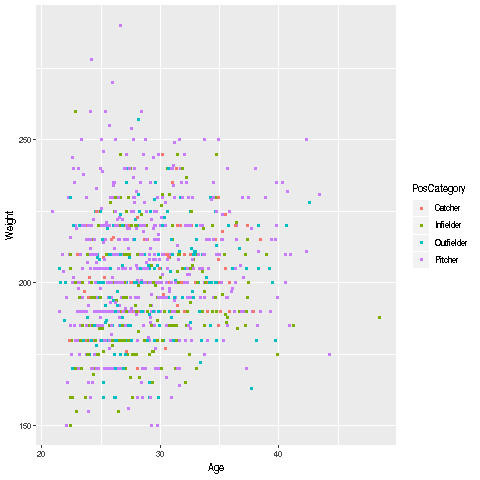
What happened here? Quite a bit, actually, so let's take this slowly.
* We took our existing (blank) plot, **p**, and by writing the'+' sign,
directed **ggplot2** to add to the plot **p**.
* Now, WHAT do we want added? We are saying, "**ggplot2**, please add
to the plot **p** whatever **geom_point** returns."
* Note that **geom_point** is a **ggplot2** function. Its task is to
produce scatter plots.
* Here are the details on the arguments to **geom_point**:
* We want to plot weight against height. We do not need to specify what
data frame these two variables are from, as we already stated that
the plot **p** is for the data frame **mlb**.
* We are also specifying that the color coding will be according to
the player position, again from **mlb**.
* When R evaluates that entire expression, **p + geom_point(aes(x = Age,
y = Weight, col = PosCategory),cex=0.6)**, the result will be another
**ggplot2** graph object. Since we typed that expression at the '>'
prompt, it was then printed to the screen as seen above.
* There is one mystery left, though: What does the function **aes**
('aesthetic") do? And why is the expression **cex=0.6** NOT an
argument to **aes**? Unfortunately, there are no easy answers to
these questions, and in a rare exception to our rule of explaining all,
we will just have to leave this as something that must be done.
One nice thing is that we automatically got a legend printed to the
right of the graph, so we know which color corresponds to which
position. We can do this in base-R graphics too, but need to set an
argument for it in **plot**.
## Lesson 28: Should You Use Functional Programming?
Earlier in this tutorial, we've found R's **tapply** function to be
quite handy. There are several others in this family, notably
**apply**, **lapply** and **sapply**. In addition, there are other
related functions, such as **do.call** and **Reduce**. And there are
a number of counterparts in the Tidyverse **purrr** package.
All of these go under the aegis of *functional programming* (FP).
To many, FP is intended as a higher-level replacement for loops, and
some members of the R community view that as desirable, even a must. I
personally take a more moderate point of view, but before discussing the
controversy, let's see how FP works as a loop-replacement.
As a simple example, say we have a nonnegative integer vector **x**, and
want code that counts doubles each element that is greater than 9.
Of course, this is something we should not use a loop with in the first
place. We should take advantage of R's vectorization capabilities:
``` r
x <- ifelse(x > 9,2*x,x)
```
But let's ignore vectorization, for the sake of illustrating the issues,
and write up a loop version:
``` r
for (i in 1:5) if (x[i] > 9) x[i] <- 2 * x[i]
```
Now, how would we replace this loop by a call to R's **sapply** function?
The latter has the call form
``` r
sapply(X,FUN)
```
where **X** is an R factor and **FUN** is a function. We will assume
here that **FUN** returns a number, not a vector or other R object. The
action of the function is to apply **FUN** on each element of **X**,
producing a new vector. (It of course can be reassigned to the old
one.)
The key is defining **FUN**:
``` r
doubleIt <- function(z) if(z > 9) return(2*z) else return(z)
sapply(x,doubleIt)
```
Let's check:
``` r
> x <- c(5,12,13,8,88)
> x <- sapply(x,doubleIt)
> x
[1] 5 24 26 8 176
```
Or, we can use what is called an *anonymous* function:
``` r
> x <- c(5,12,13,8,88)
> x <- sapply(x,function(z) if(z > 9) return(2*z) else return(z))
> x
[1] 5 24 26 8 176
```
Instead of defining the function separately, we define it right there in
the second argument of **sapply**.
Now let's consider something more elaborate. Recall our earlier
baseball player example, in which we wanted to fit separate regression
lines to each of the four player position categories. We used a loop,
which for convenience I'll duplicate here:
``` r
rownums <- split(1:nrow(mlb),mlb$PosCategory)
posNames <- c('Catcher','Infielder','Outfielder','Pitcher')
m <- data.frame()
for (pos in posNames) {
lmo <- lm(Weight ~ Age, data = mlb[rownums[[pos]],])
newrow <- lmo$coefficients
m <- rbind(m,newrow)
}
```
How might we do this in FP? We've seen the **tapply** function a couple
of times already. Now let's turn to **lapply** ("list apply"). The
call form is
``` r
lapply(VectorOrList,FUN)
```
This first argument must be a vector or list, and the second argument
must be the name of a one-argument function. This calls
**FUN** on each element of **VetorcOrList**, placing the
return values in a new list.
How might we use that here? Well, **lapply**, as the name implies, is
aimed at working on lists. Do we have any? Why yes, **rownums** is a
list!
And indeed, we do want to take some action on each element of that list:
We want to fit a linear regression model to the rows in that element.
It is natural, then, to take for **FUN** the following function:
``` r
zlm <- function(rws) lm(Weight ~ Age, data=mlb[rws,])$coefficients
```
Here **rws** is a set of row numbers, e.g. those for the pitchers. This
function calls **lm** on those rows, i.e. on the data **mlb[rws,]**,
then extracts the regression coefficients.
The code then is
``` r
> zlm <- function(rws) lm(Weight ~ Age, data=mlb[rws,])$coefficients
> w <- lapply(rownums,zlm)
```
The call to **lapply** then says, run **zlm** on each set of rows we see
in **rownums**, placing the coefficient vectors in an output list.
Specifically: Recall that the first element of **rownums** was
**rownums[['catcher']]**. So, first **lapply** will make the call
``` r
zlm(rownums[['Catcher']])
```
which will fit the desired regression model on the catcher data. Then
**lapply** will do
``` r
zlm(rownums[['Infielder']])
```
and so on. The outputs of the four **lm** calls will be returned in an
R list, which we have assigned to **w** above. Let's check the first
one:
``` r
> w[[1]]
(Intercept) Age
180.8280290 0.7949252
```
jibing with **m[1,]** in our data-frame/loop appraoch above.
Well, then, what did we accomplish -- if anything -- by using **lapply**
here rather than our earlier approach using a loop? Certainly the
**lapply** version did make for more compact code, just 2 lines. But we
had to think a harder to come up with the idea. Also, printing it
out is less compact:
``` r
> w
$Catcher
(Intercept) Age
180.8280290 0.7949252
$Infielder
(Intercept) Age
170.2465739 0.8589593
$Outfielder
(Intercept) Age
176.2884016 0.7883343
$Pitcher
(Intercept) Age
185.5993689 0.6543904
```
(Actually, we can use **sapply** here instead of **lapply**, with a
nicer printing.)
So, should beginning R coders use FP? Actually, even I, with decades of
coding experience, take a moderate approach. The criterion for
loop-based (LB) code vs. FP should be to ask these questions:
* Would FP code be easier to write than LB in this case?
* Would FP code be easier to debug than LB in this case?
* Would FP code be easier to read -- either by others, or by myself 6
months from now -- than LB in this case?
For the code in this tutorial in which we've used **tapply**, I believe
the answers to the above questions are definitely Yes. But for the
**lapply** example above, I would say the answer is No -- *especially
for beginning coders*, but even for myself.
Beginners are in the process of learning functions. FP by definition is
based on writing functions, thus making FP a more abstract and difficult
process. And I certainly disagree with the doctrinnaire view of some
that one should never write loops.
My recommendation is to take things on a case-by-case basis.
Now, let's turn to another central function in the **apply** family.
Not surprisingly, it's named **apply**! It is usually used on
**matrix** objects (like data frames, but with the contents being all of
the same type, e.g. all numerical), on either rows or columnṡ, but can
be used on data frames too.
The call form is
``` r
apply(d,rc,g)
```
Here R will apply the function **g** to each row (**rc** = 1) or column
(**rc** = 2) of the data **d**. If the function **g** returns a number,
then **apply** will return a vector.
Let's find the max values for the variables in the **pima** data:
``` r
> apply(pima,2,max)
pregnant glucose diastolic triceps insulin bmi diabetes
age
17.00 199.00 122.00 99.00 846.00 67.10 2.42
81.00
test
1.00
```
Note that to use the **apply** family, you can either use a built-in R
function, e.g. **max** here, or one you write yourself, such as **zlm**
above.
The R **apply** family includes other functions as well, They are quite
useful, but don't use them solely for the sake of avoiding writing a loop.
More compact code may not be easier.
## Lesson 29: Simple Text Processing, I
These days, text processing is big in the Data Science field, e.g. in
Natural Language Processing applications. In this lesson, we'll do a
simple yet practical example, in order to illustrate some key functions
in base-R. (R has many packages for advanced text work, such as **tm**.)
Our example will cover reading in a file of text, and compiling a word
count, i.e. calculating the number of times each word appears. This
kind of task is at the core of many text classification algorithms.
The file is
[here](https://raw.githubusercontent.com/matloff/fasteR/master/data/aboutR.txt).
It's basically the About section of the [R Project home
page](https://www.r-project.org/). Here are the first few lines:
```
What is R?
Introduction to R
R is a language and environment for statistical computing and graphics.
```
Now, how can we read the file? For instance, **read.table** won't work,
as it expects the same number of nonblank fields on each line. As you
can see above, our file has a variable number of such fields per line.
Instead, we read the lines of the file via a function named, not
surprisingly, **readLines**:
``` r
> abt <- readLines('https://raw.githubusercontent.com/matloff/fasteR/master/data/aboutR.txt')
```
So, what exactly is in **abt** now? Let's turn to our usual inspection
tool, **str**.
``` r
> str(abt)
chr [1:70] "" "What is R?" "" "Introduction to R" "" ...
```
So, **abt** is a vector of 70 elements, of type character. Each element
of this vector is one line from the file:
```
> head(abt)
[1] ""
[2] "What is R?"
[3] ""
[4] "Introduction to R"
[5] ""
[6] " R is a language and environment for statistical computing and graphics."
```
The first line in the file was empty, so **abt[1]** is "", and so on.
Recall, our goal here is to tabulate the various words in the file. We
won't be tabulating each individual line, so let's just make one long
line out of **abt**.
The main R function for concatening strings is **paste**. For
instance,
``` r
> paste('abc','987')
[1] "abc 987"
```
It can also be applied on an element-by-element basis in a vector, but
as noted, we want to create one long vector. The **collapse** argument
does that for us:
``` r
abt1 <- paste(abt,collapse=' ')
```
This says, "Take all the 70 strings in **abt**, and collapse them into one
big string, with a single space separating each of the original
strings." So, it joined the elements of **abt** into one long string,
**abt1**, with successive elements of **abt** being separated by a
blank (in addition to whatever blanks were in the original strings).
``` r
> str(abt1)
chr " What is R? Introduction to R R is a language and environment for statistical computing and graphics. I"| __truncated__
```
So, **abt1** is now a single character string. We can inspect parts of
it with the **substr** function,, e.g.
``` r
> substr(abt1,288,336)
[1] "nd colleagues. R can be considered as a differ"
```
tells us the 288th through 336th characters in **abt1**. How many
characters are in **abt1** in all?
``` r
> nchar(abt1)
[1] 3461
```
We now need to break **abt1** down into individual words. We can do so using
**strsplit**:
``` r
> y <- strsplit(abt1,' ')
> str(y)
List of 1
```
That second argument, ' ', means we want the blank character to be our
splitting delimiter. In some other setting, we may wish to use, say, a
comma as the splitting delimiter, or whatever.
Now let's look at **y**. Keeping in mind that that object is an R list,
we can use double brackets to inspect the first element of **y** (which
is the *only* element of **y**, as we saw above that **y** is a "list of
1").
``` r
> str(y[[1]])
chr [1:722] "" "What" "is" "R?" "" "Introduction" "to" "R" "" "" "" "" "R" ..
```
So, **y[[1]]** is a character vector of length 722. There is one
element for each word in the original text, though some of the "words"
are actually empty. We see here that the first word in the text,
**y[[1]][1]**, was empty, the second word, **y[[1]][2]**, was 'What',
the third was 'is' and so on.
> 📘 **ALWAYS KEEP IN MIND**
>
> When one gets to this level of R (or for that matter, *any* language)
, it is crucial to pay close attention
> to the class and size of all R objects.
>
> Here we have:
>
> * **abt** is a character vector of length 70 (70 lines in the text)
> * **abt1** is a character vector of length 1 (entire text in 1 long string)
> * **y** is an R list of length 1
> * **y[[1]]** is a character vector of length 722 (722 words in text)
> * **y[[1]][1]**, **y[[1]][2]** etc. are strings (1st word, 2nd word...)
>
> Subtle differences between object types can make big
> differences in actions.
>
> *Dealing with this is not rocket science, just something that
> requires patience.* You the reader should take some time at this point to
> ensure that you understand the above accounting for the various
> variables.
Now, why does the R list **y** have length only 1? The answer is that
only string was fed into **strsplit**. Recall what we did:
``` r
> y <- strsplit(abt1,' ')
```
If **abt1** had consisted of, say, 5 strings rather than just 1, **y**
would have been an R list of 5 elements.
At some places in the original input, we had several consecutive blanks.
When there is more than one consecutive blank, the **strsplit** function
treats the excess blanks as "words." (This comes as quite a surprise to
Python programmers.)
So, how to get rid of the blank "words"?
``` r
> y1 <- y[[1]] # easier to read, less cluttered
> allWords <- y1[y1 != ''] # != means "not equal to"
> allWords
> allWords
[1] "What" "is"
[3] "R?" "Introduction"
[5] "to" "R"
...
```
The expression
``` r
y1[y1 != '']
```
may look a little mysterious, but actually it works in the same way as
we've seen before in extracting subsets of vectors, data frames and so
on:
1. As noted, **!=** means not equal, so **!= ''** means "not an empty word."
(Warning: This will cause some double negatives below. Again, just
be patient (the supreme trait of any programmer).
2. Remember, each element of **y1** is a "word," 722 of them. We saw
above that the first word is '', i.e. an empty string, the
second is "What" and so on. The expression **y1 != ''** produces
722 TRUEs and FALSEs, the first one being FALSE (no, the first word
was not nonempty), the second one being TRUE (yes, the second word was
nonempty), etc.
3. As we saw before, a vector (**y1** here) evaluated
at indices taking on TRUE and FALSE values will retain the
vector elements corresponding to the TRUEs. In other words, the
expression **y1[y1 != '']** consists of the nonempty words.
So, **allWords** is just what we need---the original file contents broken down
into individual words, with no empty words.
A couple of other points:
* '!' means "not" in R, e.g.
``` r
> 3 < 8
[1] TRUE
> !(3 < 8)
[1] FALSE
```
* Material following '#' is a `comment`, a note the programmer inserts
to explain the code, for clarity and future maintainability, to
aid him/herself and/or others who read the code. (In many cases,
comments are here to benefit you, the reader.)
We'll continue with this example in the next lesson, but first, time for
a **Your Turn** session.
> ❄️ Your Turn
>
> Write code to determine which line in
> **abt** is longest, in terms of the number of characters.
## Lesson 30: Simple Text Processing, II
Now, let's complete our goal of producing a word count for the original
text, i.e. which words appeared in the text and how many times did each
one appear?
As usual, it is a must to inspect the result, say the first 25 elements:
``` r
> head(allWords,25)
[1] "What" "is" "R?"
[4] "Introduction" "to" "R"
[7] "R" "is" "a"
[10] "language" "and" "environment"
[13] "for" "statistical" "computing"
[16] "and" "graphics." "It"
[19] "is" "a" "GNU"
[22] "project" "which" "is"
[25] "similar"
```
Good, all the words seem to be there, and the "" are NOT there, just as
desired. But how to get the word counts? Why, it's our old friend,
**tapply**!
``` r
> q <- tapply(allWords,allWords,length)
> head(q,25)
; …) “environment” (easily) (formerly
1 1 1 1 1
(including (linear * © a
1 1 5 1 13
about accretion activity. add additional
3 1 1 1 1
Advanced algorithmic allows an analysis
1 1 1 5 2
analysis, and are around arrays,
2 27 4 1 1
```
We got rid of the blank words, but the report here is still a little
rough, for example treating ';' as a "word." But overall, it's doing
what we want, showing for instance that the word "analysis" occurs 2
times in the original text.
Now, how did this call to **tapply** work here? Actually, this is
really the same pattern we saw with **tapply** before, with the
**length** function as our third argument. It may look a little odd
that the first two arguments are identical, but it makes sense:
1. The first argument says we want to split up the **allWords** vector into
piles.
2. The second argument says we want the *definition* of the piles to
also be based on **allWords**. In other words, we want a separate
pile for each distinct word.
3. Each entity that we are informally calling a "pile" above is an R
vector:
``` r
> str(allWords)
chr [1:515] "What" "is" "R?" "Introduction" "to" "R" "R" "is" "a" ...
```
Applying the **length** function to each vector gives us the count
in each pile, exactly what we needed.
> 📘 Pro Tip
>
> In coding, certain patterns do arise often, such as the
> **tapply(x,x,length)** trick we saw here. In fact,
> there are even coding books with "design patterns" in their titles.
> Take note when you see the same pattern a lot, as it may come in handy.
We're not fully done yet. For instance, we have a punctuation problem,
where periods, commas and so on are considered parts of words, such as
the period in **allWords[17]** seen above, 'graphics.' We also probably
should change capital letters to lower case, so that 'What' and 'what'
are not counted as two different words.
For major usage, we should consider using one of the advanced R packages
in text processing. For instance, the **tm** package has a
**removePunctuation** function. But let's see how we can do this with
the basics.
We'll use R's **gsub** function. Its call form, as we'll use it, is
``` r
gsub(string_to_change,replacement,input_vector,fixed=TRUE)
```
E.g.
``` r
> a <- c('abc','de.')
> gsub('.','',a,fixed=TRUE) # replace '.' by empty string
[1] "abc" "de"
```
(The **fixed** argument is complex, and pops up in all the R string
manipulation packages. This again is something you should use for now,
and look into when you become more skilled at R.)
So, to remove all periods in **allWords**, we can do:
``` r
> awNoPers <- gsub('.','',allWords,fixed=TRUE)
> awNoPers[17] # check that it worked
[1] "graphics"
```
We could continue to fine-tune the output in this manner.
## Lesson 31: Linear Regression Analysis, II
Continuing our look at linear regression analysis using R, let's look at
the famous [bike sharing
data](ttps://archive.ics.uci.edu/ml/datasets/bike+sharing+dataset).
(See the latter site for the documentation; e.g. temperature has been
scaled, rather than measured in degrees.)
It's in a **.zip** file, so it will need a little extra preprocessing:
``` r
# fetch from Web, and store the downloaded data to the file 'bike.sip'
> download.file('https://archive.ics.uci.edu/ml/machine-learning-databases/00275/Bike-Sharing-Dataset.zip','bike.zip')
> unzip('bike.zip') # out come the files 'day.csv' and 'hour.csv'
> day <- read.csv('day.csv',header=TRUE)
> head(day) # always take a look around!
instant dteday season yr mnth holiday weekday workingday weathersit
1 1 2011-01-01 1 0 1 0 6 0 2
2 2 2011-01-02 1 0 1 0 0 0 2
3 3 2011-01-03 1 0 1 0 1 1 1
4 4 2011-01-04 1 0 1 0 2 1 1
5 5 2011-01-05 1 0 1 0 3 1 1
6 6 2011-01-06 1 0 1 0 4 1 1
temp atemp hum windspeed casual registered cnt
1 0.344167 0.363625 0.805833 0.1604460 331 654 985
2 0.363478 0.353739 0.696087 0.2485390 131 670 801
3 0.196364 0.189405 0.437273 0.2483090 120 1229 1349
4 0.200000 0.212122 0.590435 0.1602960 108 1454 1562
5 0.226957 0.229270 0.436957 0.1869000 82 1518 1600
6 0.204348 0.233209 0.518261 0.0895652 88 1518 1606
```
By the way, the weather variables have been rescaled to the interval
[0,1]. A value of 0.28, for instance, means 28% of the way from the
minimum to the maximum value of this variable.
One new concept here is the presence of *indicator* variables, more
informally known as *dummy variables*. These are variables taking only
the values 0 and 1, with a 1 "indicating" that some trait is present.
For instance, the **holiday** variable is either 1 or 0, depending on
whether that day was a holiday (which might affect the demand for bikes
that day).
Those who manage this bike sharing service may wish to predict future
demand for bikes, say the next day, to aid in their planning. As an
example, let's try to predict the number of casual riders from some
weather variables and the dummy variable **workingday**.
``` r
> day1 <- day[,c(8,10,12:14)]
> head(day1)
workingday temp hum windspeed casual
1 0 0.344167 0.805833 0.1604460 331
2 0 0.363478 0.696087 0.2485390 131
3 1 0.196364 0.437273 0.2483090 120
4 1 0.200000 0.590435 0.1602960 108
5 1 0.226957 0.436957 0.1869000 82
6 1 0.204348 0.518261 0.0895652 88
> lmout <- lm(casual ~ .,data=day1)
> lmout
...
Coefficients:
(Intercept) workingday temp hum windspeed
1063.6 -806.6 2149.5 -812.7 -1145.3
```
The expression "casual ~ ." means, "regress **casual** against all the
other variables in this dataset.
These numbers make sense. The negative coefficient for **workingday**
says that, all else equal, there tend to be fewer casual riders on a
work day.
By the way, we probably should expect fewer riders on very
cold or very hot days, so we may wish to add a quadratic term to the
model, say by doing
``` r
day1$temp2 <- temp^2 # the caret symbol means exponentiation,
# i.e. 2nd power here
```
This would add the indicated column to **day1**. But we will not pursue
this for now.
One of the very important features of R is *generic functions*. These
are functions that take on different roles for objects of different
classes. One such example is the **plot** function we saw earlier.
Try typing "plot(lmout)" at the R prompt. You will be shown several
plots desribing the fitted regression model. What happened was that the
function **plot** is just a placeholder. When we type "plot(lmout)" R
says, "Hmm, what kind of object is **lmout**? Oh, it's of class
**'lm'**. So I'm going to transfer (*dispatch*) this call to one
involving a special plot function for that class, **plot.lm**." This is
in contrast to our previous calls to **plot**, which were invoked on
vectors; those calls were dispatched to **plot.default**.
Another generic function is **summary**:
``` r
> summary(Nile)
Min. 1st Qu. Median Mean 3rd Qu. Max.
456.0 798.5 893.5 919.4 1032.5 1370.0
> summary(lmout)
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1063.55 101.37 10.492 < 2e-16 ***
workingday -806.63 33.41 -24.143 < 2e-16 ***
temp 2149.52 86.32 24.901 < 2e-16 ***
hum -812.74 112.98 -7.194 1.57e-12 ***
windspeed -1145.31 208.55 -5.492 5.51e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
...
```
In the first case, the call to **summary**, invoked on a vector, was
dispatched to **summary.default**, while in the second the transfer was
to **summary.lm**. In both cases, whoever it was in the R development
team who wrote these functions decided what summary information should
be printed out automatically.
Again, the purpose of this tutorial is to present R, not statistics.
The interested reader should consult a statistics book regarding
*p-values* and *confidence intervals.* The former are show in the last
column of the above summary. An approximate 95% confidence interval
for, say, the population coefficient of humidity is -812.74 plus or
minus 1.96 times the *standard error*, 112.98. Note carefully that
p-values have long been considered to be poor methodology; see
the [ASA statement](https://amstat.tandfonline.com/doi/full/10.1080/00031305.2016.1154108).
Another important generic function is **predict**. Say we want to
predict **casual** for a work day in which **temp**, **hum** and
**windspeed** are 0.26, 0.55, 0.18, respectively.
``` r
> newCase <- data.frame(workingday=1, temp=0.26, hum=0.55, windspeed=0.18)
> predict(lmout,newCase)
1
162.6296
```
The **predict** function, which here is **predict.lm**, assumes that the
new cases to be predicted are supplied as a data frame, with the same
column names as with the original data.
## Lesson 32: Work with the R Date Class
In the bike sharing data, dates were included, in **day$dteday**. As
noted, some of those were holidays, indicated in the **holiday** column.
Let's see how many holidays there were:
``` r
> hds <- day$dteday[day$holiday == 1]
> hds
[1] 2011-01-17 2011-02-21 2011-04-15 2011-05-30 2011-07-04 2011-09-05
[7] 2011-10-10 2011-11-11 2011-11-24 2011-12-26 2012-01-02 2012-01-16
[13] 2012-02-20 2012-04-16 2012-05-28 2012-07-04 2012-09-03 2012-10-08
[19] 2012-11-12 2012-11-22 2012-12-25
```
Once again, let's review how the above code works. The expression "[day$holiday == 1]" yields a bunch of TRUEs and FALSEs. Using them as indices in the vecotr **day$dteday** gives us exactly the dates that are holidays.
We see above that there were 21 holidays during the time period of the
data. But we can do more. First, what kind of object is **hds** above?
``` r
> class(hds)
[1] "factor"
```
Fine, but R has a special class for date data, not surprisingly called
**'Date'**. Let's convert to that class:
``` r
> hd <- as.Date(hds)
> class(hd)
[1] "Date"
> hd
[1] "2011-01-17" "2011-02-21" "2011-04-15" "2011-05-30" "2011-07-04"
[6] "2011-09-05" "2011-10-10" "2011-11-11" "2011-11-24" "2011-12-26"
[11] "2012-01-02" "2012-01-16" "2012-02-20" "2012-04-16" "2012-05-28"
[16] "2012-07-04" "2012-09-03" "2012-10-08" "2012-11-12" "2012-11-22"
[21] "2012-12-25"
```
Though it prints out just as before, there are extra properties now, and
even bettery, in POSIX form:
``` r
> hp <- as.POSIXlt(hd)
> hp
[1] "2011-01-17 UTC" "2011-02-21 UTC" "2011-04-15 UTC" "2011-05-30 UTC"
[5] "2011-07-04 UTC" "2011-09-05 UTC" "2011-10-10 UTC" "2011-11-11 UTC"
[9] "2011-11-24 UTC" "2011-12-26 UTC" "2012-01-02 UTC" "2012-01-16 UTC"
[13] "2012-02-20 UTC" "2012-04-16 UTC" "2012-05-28 UTC" "2012-07-04 UTC"
[17] "2012-09-03 UTC" "2012-10-08 UTC" "2012-11-12 UTC" "2012-11-22 UTC"
[21] "2012-12-25 UTC"
> hp[16]$wday # what day of the week was July 4, 2012?
[1] 3
# ah, Wednesday (code 3)
```
(The UTC parts are the times of day, which we had not supplied.)
There are many operations that can be done on R dates. The above is
just a little sample.
## Lesson 33: Tips on R Coding Style and Strategy
Programming is a creative activity, and thus different programmers will
have different coding styles. Some people feel so strongly that they
will publish there own particular style guides, such as
[this one](https://google.github.io/styleguide/Rguide.xml)
by the R community at Google. Mine is
[here`](https://github.com/matloff/R-Style-Guide).
Needless to say, style is a matter of personal taste. But:
**Style IS important for any code you intend to use again, for two reasons:**
1. You will quickly forget how your code works.
2. If you share your code with others, you need to make its workings
clear to them.
**Equally important is strategy, the way you approach a coding project.**
There is no magic formula on how to write code. As noted earlier, I
cannot *teach* yow how to code. I can only show you how the
ingredients work -- loops, variables, functions, if/else etc. -- and you
must creatively put them together into code that achieves goals. It's
like solving a big puzzle, and like many big puzzles, you may need to
ponder the problem for quite a while, gaining insights here and there
until it's finally done. Yet, as with coding style, there are strategies
that we all agree on.
So in spite of great individual variation, there are common aspects that
everyone agrees with, which we'll discuss in this lesson.
**Comment your code:**
In any programming course for Computer Science students, this
is absolutely central. If a student turns in a programming assignment
with few or no comments, it will get a failing grade. If comments are
needed for clarity and readability for CS students, who are presumably
strong programmers, then R users who are not expert programmers need
comments even more.
A [style
guide](https://www.cs.utah.edu/~germain/PPS/Topics/commenting.html)
at a top university computer science department puts it well:
> Commenting involves placing Human Readable Descriptions inside of
> computer programs detailing what the Code is doing. Proper use of
> commenting can make code maintenance much easier, as well as helping
> make finding bugs faster. Further, commenting is very important when
> writing functions that other people will use. Remember, well
> documented code is as important as correctly working code.
(Also see specific tips on commenting, later in that document.)
*Don't be under the illusion that your code is self-documenting; it
isn't! A typical comment might look like this:*
``` r
w <- f(w)
# at this point, the data frame w will consist of the original rows for
# people over age 65 and who are homeowners
```
*At the top of each source file, insert comments giving the reader an
overview of the contents.*
This will typically an overview of the roles of each major function, how
the functions interact with each other, what the main data structures
are, and so on.
I strongly recommend that you write these comments at the top of a file
BEFORE you start coding (and of course modifying it as you do write
code). This will really help you focus during the coding process.
**Indent your code:**
``` r
if (x < y) {
x <- y^2
z <- x + y
}
```
is much easier to read than
``` r
if (x < y) {
x <- y^2
z <- x + y
}
```
**Write your code in top-down fashion:**
If you have a function **f** that is more than, say, a dozen lines long,
break its code into calls to smaller functions, say **g** and **h**.
Then **f** will consist of those calls, plus some "glue" lines to deal
with the return values and so on. Of course, it's a matter of taste as
to break things up that way, but the point is that it makes your code
both easier to *read* (by others, or by yourself later), and even more
important, easier to *write*. Breaking up the code like this makes it
read like an outline.
**Don't skimp on attending to the "corner cases":**
Computer Science people talk about "corner cases," meaning special
situations in which code may fail in spite of being generally sound.
For instance, consider this code:
``` r
> i <- 5
> 1:i
[1] 1 2 3 4 5
```
But what about the special case in which **i = 0**?
``` r
> i <- 0
> 1:i
[1] 1 0
```
This may not be what you wanted. You probably should insert a check,
say
``` r
if (i >= 1) i:5
```
and maybe also code to handle the erroneous case. This will depend on
the situation, but the main point is to be aware of possible corner
cases.
**Use a debugging tool:**
More on this in a later lesson!
## Lesson 34: The Logistic Model
In our earlier examples of regression analysis, we were predicting a
continuous variable such as human weight. But what if we wish to
predict a *dichotomous* varible, i.e. one recording which of two
outcomes occurs?
Consider the Pima dataset from earlier examples. Say we are predicting
whether someone has -- or will later develop -- diabetes. This is coded
in the **test** column of the dataset, 1 for having the disease, 0 for
not.
As a simple example, say we try to predict **test** from the variables
**bim** and **age**. A linear model would be
mean test = β0 + β1 bmi + β2 age
Remember, **test** takes on the values 1 and 0. What happens when we
take the average of a bunch of 1s and 0s? The answer is that we get the
proportion of 1s. For instance, the mean of the numbers 1,0,1,1 is 3/4,
which is exactly the proportion of 1s in that data.
In statististical terms, what the above equation is doing is expressing
the probability of a 1 -- i.e. the probability of having diabetes --
in terms of Body Mass Index and age.
Not a bad model, but one troubling point is that the right-hand side
could evaluate to a number less than 0 or greater than 1, which would be
impossible for a probability. In order to deal with that problem, we
might use a *logistic* model, as follows.
Define the logistic function to be
l(t) = 1 / (1 + e-t)
We then modify the above equation to
probability of diabetes = l(β0 + β1 bmi + β2 age)
As before, the statistical details are beyond the scope of this
R tutorial, but here is how you estimate the coefficients
βi using R:
``` r
> glout <- glm(test ~ bmi + age, data=pima, family=binomial)
> summary(glout)
...
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -5.40378 0.51530 -10.487 < 2e-16 ***
bmi 0.09825 0.01248 7.874 3.45e-15 ***
age 0.04561 0.00694 6.571 4.98e-11 ***
...
```
Let's explore those estimated βi a bit. Consider
women with about average BMI, say 32, and compare 30-year-olds to those
of age 40.
``` r
> l <- function(t) 1 / (1 + exp(-t))
> l(-5.40378 + 32*0.09825 + 30*0.04561)
[1] 0.2908045
> l(-5.40378 + 32*0.09825 + 40*0.04561)
[1] 0.3928424
```
So, the risk of diabetes increases substantial over that 10-year period,
but this population and BMI level.
## Lesson 35: Files and Folders/Directories
Note: On Unix-family systems such as Linux, the Windows term *folder*
is said to be a *directory*. You will frequently see this in Mac
discussions as well. (The Mac OS is a Unix-family system.) We will
typically use the term *directory* here, as that is what R uses.
In assembling a dataset for my **regtools** package, I needed to collect
the records of several of my course offerings. I started in a directory
that had one subdirectory for each offering. In turn, there was a file
named **Results**. As an intermediate step, wanted to find all such
files, placing the text for each one in an R list **gFiles**. Only some
specific columns of each file will be retained. (The discussion here is
a slightly adapted version.)
The chief R functions I used were:
* **list.dirs:** Returns a character vector with the names of all the
directories (i.e. subdirectories) within the current directory.
* **dir:** Returns a character vector with the names of all files
within the current directory.
* **%in%:** Determines whether a specified object is an element in a
specified vector.
* **setwd:** Changes to the specified directory.
Here is the code:
``` r
getData <- function() {
currDir <- getwd() # leave a trail of bread crumbs
dirs <- list.dirs(recursive=FALSE)
numCourseOfferings <- 0
# create empty R list, into which we'll store our course records
resultsFiles <- list()
for (d in dirs) {
setwd(d) # descend into d directory
# check if there is a Results file there
fls <- dir()
if (!('Results' %in% fls)) { # not there, skip this dir
setwd(currDir)
next
}
# ah, there is such a file; increment our count
numCourseOfferings <- numCourseOfferings + 1
# open it
resultsLines <- readLines('Results')
# delete the comment lines; look at 1st character in each line
resultsLines <- delComments(resultsLines)
resultsFiles[[numCourseOfferings]] <- extractCols(resultsLines)
setwd(currDir)
}
resultsFiles # return all the grades records
}
```
Before we go into the details, note the following:
* The code is written in a top-down manner. Much of the work of
**getData** is offloaded to other functions (code not shown),
**delComments** and **extractCols**.
* There are lots of comments!
Now, consider the line
``` r
dirs <- list.dirs(recursive=FALSE)
```
As mentioned, **list.dirs** will determine all the subdirectories
within the current directory. But what about subdirectories of
subdirectories, and subdirectories of subdirectories of subdirectories,
and so on? Setting **recursive** to FALSE means we want only
first-level subdirectories.
So, the line
``` r
for (d in dirs) {
```
will then have us process each (first-level) directory, one by one.
When we enter one of those subdirectories, the line
``` r
fls <- dir()
```
will determine all the files there, storing the result as a character
vector **fls**.
Then, as the comment notes, the lines
``` r
if (!('Results' %in% fls)) { # not there, skip this dir
setwd(currDir)
next
}
```
will, in the event that there is no **Results** file in this
subdirectory, skip this subdirectory. The R keyword **next** says, "Go
to the next iteration of this loop," which here means to process the
next subdirectory. Note that to prepare for that, we need to move back
to the original directory:
``` r
setwd(currDir)
```
On the other hand, if this subdirectory *does* contain a file named
**Results**, the remaining code increments our count of such files,
reads in the found file, and assigns its contents as a new element of
our **resultsFiles** list.
We've seen R **for** loops in previous lessons, but there's another kind
of loop, **while**. It keeps iterating until some specified condition
is met. We don't know how many iterations will be needed, unlike the
**for** case, with a fixed number of iterations.
As our example, consider r's built-in dataset **AirPassengers**, which
consists of number of air travelers in thousands, in monthly data from
January 1949. As usual, let's glance at it first:
``` r
> airpass <- AirPassengers # less typing below
> str(airpass)
Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...
```
Suppose we wish to know when the cumulative number of passengers first
exceeded 10 million. A crude way would be to use R's **cumsum**
("cumulative sums") function:
``` r
> cumsum(airpass)
[1] 112 230 362 491 612 747 895 1043 1179 1298 1402 1520
[13] 1635 1761 1902 2037 2162 2311 2481 2651 2809 2942 3056 3196
[25] 3341 3491 3669 3832 4004 4182 4381 4580 4764 4926 5072 5238
[37] 5409 5589 5782 5963 6146 6364 6594 6836 7045 7236 7408 7602
[49] 7798 7994 8230 8465 8694 8937 9201 9473 9710 9921 10101 10302
[61] 10506 10694 10929 11156 11390 11654 11956 12249 12508 12737 12940 13169
[73] 13411 13644 13911 14180 14450 14765 15129 15476 15788 16062 16299 16577
[85] 16861 17138 17455 17768 18086 18460 18873 19278 19633 19939 20210 20516
[97] 20831 21132 21488 21836 22191 22613 23078 23545 23949 24296 24601 24937
[109] 25277 25595 25957 26305 26668 27103 27594 28099 28503 28862 29172 29509
[121] 29869 30211 30617 31013 31433 31905 32453 33012 33475 33882 34244 34649
[133] 35066 35457 35876 36337 36809 37344 37966 38572 39080 39541 39931 40363
```
We see that that occurred in the 60th month. But though this approach
would be convenient, it also would be wasteful: We are calculating *all*
the cumulative sums, even though we don't need them all. In a really
long vector, this could be slow. Here is a less wasteful way:
``` r
tot <- 0
i <- 1
while (i <= length(airpass) && tot < 10000) { ## && means 'and'
i <- i + 1
tot <- tot + airpass[i]
}
i # prints 60
```
So, the **while** loop keeps iterating until we get the desired
cumulative total.
Key points here:
* The **<=** operator means "less than or equal to." There is also
**>=** for "greater than or equal to."
* The **&&** operator stands for "and". It is slightly different from
the **&** operator, which involves vector operands.
* The condition within the 'while' says that (a) we are not yet at the
end of the **airpass** vector, AND (b) our total is still less than 10000.
* Note the need for the condition **i <= length(airpass)**. It's
possible that **tot** will never exceed 10000 (not true here, but we
wouldn't know that *a priori*), so we need that condition so that the
loop doesn't iterate forever!
There's more, though. The **cumsum** function is vectorized, so using
it, though seemingly wasteful, may actually be faster than the loop
These are books and other resources that I myself consult a lot (yes, I
do consult my own books; can't keep it all in my head :-) ), plus others
I recommend.
**Nonprogramming Coverage of R**
* Andrie de Vries and Joris Meys, *R For Dummies* (second edition), For
Dummies
* Jaren Lander, *R for Everyone: Advanced Analytics and Graphics*
(second ed.), Addison-Wesley
**R Programming and Language**
* John Chambers, *Software for Data Analysis: Programming with R*, Springer
* Dirk Eddelbuettel, *Seamless R and C++ Integration with Rcpp*,
Springer
* Colin Gillespie and Robin Lovelace, *Efficient R Programming: A
Practical Guide to Smarter Programming*
* Norm Matloff, *The Art of R Programming*, NSP
* Norm Matloff, *Parallel Computation for Data Science*, CRC
* Hadley Wickham, *Advanced R* (second edition), CRC
**Data Science with R**
* Nina Zumel and John Mount, *Practical Data Science with R*, Manning
(2nd ed.)
* Hadley Wickham and Garrett Grolemund, *R for Data Science: Import,
Tidy, Transform, Visualize, and Model Data*, O'Reilly
**Graphics in R**
* Winston Chang, *R Graphics Cookbook: Practical Recipes for Visualizing Data*, O'Reilly
* Paul Murrell, *R Graphics* (third edition), CRC
* Deepayan Sarkar, *Lattice: Multivariate Data Visualization with R*,
Springer
* Hadley Wickham, *ggplot2: Elegant Graphics for Data Analysis*, Springer
**Regression Analysis and Machine Learning, Using R**
* Francis Chollet and JJ Allaire, *Deep Learning in R*, Manning
* Julian Faraway, *Linear Models with R*, CRC
* Julian Faraway, *Extending the Linear Model with R*, CRC
* John Fox and Sanford Weisberg, *An R Companion to Applied Regression*,
SAGE
* Frank Harrell, *Regression Modeling Strategies: With Applications to
Linear Models, Logistic and Ordinal Regression, and Survival Analysis*,
Springer
* Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani,
*Introduction to Statistical Learning: with Applications in R*,
Springer, 2nd ed.
* Max Kuhn, *Applied Predictive Modeling*, Springer
* Max Kuhn and Kjell Johnson, Feature Engineering and Selection: *A
Practical Approach for Predictive Models*, CRC
* Norm Matloff, *Statistical Regression and Classification: from Linear
Models to Machine Learning*, CRC
* Norm Matloff, *The Art of Machine Learning: Algorithms+Data+R*, NSP,
coming January 2024
**Other**
* Rob Hyndman and George Athanasopoulos, *Forecasting: Principles and Practice*,
OTexts
* Ted Kwartler, *Text Mining in Practice with R*
* Norm Matloff, *Probability and Statistics for Data Science: Math + R +
Data*, CRC
* Julia Silge and David Robinson, *Text Mining with R: A Tidy Approach*,
O'Reilly
* Yihui Xie *et al*, *R Markdown: The Definitive Guide*, CRC
**Web**
I also would recommend various Web tutorials:
* Szilard Palka,
[CEU Business Analytics program: Use Case Seminar 2 with Szilard Pafka (2019- 05-08)](https://t.co/kbhw44Tbbn)
* Hadley Wickham,
[the Tidyverse](https://www.tidyverse.org)
## Thanks
author is grateful to Kyle Butts for some format improvements in July
2022.
This tutorial has also benefited from feedback from (in alphabetical order)
Clay Ford, Reese Goding, Ira Sharenow, and Aaron Wichman, as well as
numerous anonymous suggestions.
An *interactive development environment* (IDE) is a software tool that
enables editing, saving and running your code, as well as related
actions such as installing packages.
The real "power users" tend to use either Emacs Speaks Statistics (ESS),
a plugin for the Emacs editor, or Nvim-r,, a plugin for the vim editor.
However, since this tutorial is aimed at those with little or no prior
coding background, we will not cover them. Instead, we introduce
RStudio. Here are some pros and cons:
* RStudio is very highly popular, especially in the US and Australia/New
Zealand. Indeed, for many users, RStudio *is* R.
* Lots of help available on the Web, and in R User Groups that have been
established in many major cities. Has numerous features, keyboard
shortcuts etc.
* That however also has a downside, since as noted earlier, the
compexity of RStudio can be "overwhelming."
In light of that last point, we recommend that you NOT try to learn
RStudio to any degree of complexity at the outset. Just learn how to
create, load, run, and save files of R code, the simple stuff, which
should be easy. Leave the advanced features for later.
### Installation
There are many tutorials on the Web for installing RStudio.
[This one](https://techvidvan.com/tutorials/install-r/) is pretty good,
for all major platforms.
### Startup
If your screen has an RStudio icon, click it. Otherwise type 'rstudio'
into a terminal window.
### Basic actions:
Again, there is a lot more one can do than the following, but we'll
stick to the absolute basics.
Note the pane in the lower-left portion of the RStudio screen. By
default, that is the Console pane, containing the usual R '>' prompt.
You can use it just as we have throughout this tutorial. Note too that
this is where your R output will appear.
Everything here involves files, where we store our R code (*scripts*).
**creating a new code file:** File | New File | R Script will create an
empty window pane, ready to be filled with code. Start typing!
**saving a code file:** File | Save will save the contents of the pane.
If it's a new file, you'll be asked to give the file a name. Make sure
to note what folder the file will be in, so you know where to read it
from later.
**running code:** To run the code in your current window, choose Code |
Run Region | Run All.
**exiting RStudio:**
File | Quit Session...
## LICENSING
The document is covered by a
[Creative Commons](http://creativecommons.org/licenses/by-nd/3.0/us/) license,
Creative Commons Attribution-No Derivative Works 3.0 United States
. I have
written the document to be *used*, so readers, teachers and so on are
very welcome and encouraged to copy it verbatim. Copyright is retained
by N. Matloff in all non-U.S. jurisdictions, but permission to use these
materials in teaching is still granted, provided the authorship and
licensing information here is displayed. I would appreciate being
notified if you use this book for teaching, just so that I know the
materials are being put to use, but this is not required. information
displayed. No warranties are given or implied for this material.