https://github.com/meshpro/meshzoo
A collection of meshes for canonical domains
https://github.com/meshpro/meshzoo
mesh-generators python
Last synced: about 2 months ago
JSON representation
A collection of meshes for canonical domains
- Host: GitHub
- URL: https://github.com/meshpro/meshzoo
- Owner: meshpro
- Created: 2016-04-26T11:57:19.000Z (almost 10 years ago)
- Default Branch: main
- Last Pushed: 2024-01-19T10:19:50.000Z (about 2 years ago)
- Last Synced: 2025-10-21T20:50:36.223Z (4 months ago)
- Topics: mesh-generators, python
- Homepage:
- Size: 2.46 MB
- Stars: 333
- Watchers: 11
- Forks: 42
- Open Issues: 1
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
[](https://pypi.org/project/meshzoo/)
[](https://pypi.org/project/meshzoo/)
[](https://github.com/nschloe/meshzoo)
[](https://pepy.tech/project/meshzoo)
[](https://discord.gg/PBCCvwHqpv)
When generating meshes for FEM/FVM computations, sometimes your geometry is so simple
that you don't need a complex mesh generator (like
[pygmsh](https://github.com/meshpro/pygmsh/),
[MeshPy](https://github.com/inducer/meshpy),
[mshr](https://bitbucket.org/fenics-project/mshr),
[pygalmesh](https://github.com/meshpro/pygalmesh/),
[dmsh](https://github.com/meshpro/dmsh/)),
but something simple and fast that makes use of the structure of the domain. Enter
meshzoo.
### Installation
Install meshzoo [from PyPI](https://pypi.org/project/meshzoo/) with
```
pip install meshzoo
```
### How to get a license
Licenses for personal and academic use can be purchased
[here](https://buy.stripe.com/5kA3eV8t8af83iE9AE).
You'll receive a confirmation email with a license key.
Install the key with
```
plm add
```
on your machine and you're good to go.
For commercial use, please contact support@mondaytech.com.
### Examples
#### Triangle

```python
import meshzoo
bary, cells = meshzoo.triangle(8)
# corners = np.array(
# [
# [0.0, -0.5 * numpy.sqrt(3.0), +0.5 * numpy.sqrt(3.0)],
# [1.0, -0.5, -0.5],
# ]
# )
# points = np.dot(corners, bary).T
# Process the mesh, e.g., write it to a file using meshio
# meshio.write_points_cells("triangle.vtk", points, {"triangle": cells})
```
#### Rectangle


```python
import meshzoo
import numpy as np
points, cells = meshzoo.rectangle_tri(
np.linspace(0.0, 1.0, 11),
np.linspace(0.0, 1.0, 11),
variant="zigzag", # or "up", "down", "center"
)
points, cells = meshzoo.rectangle_quad(
np.linspace(0.0, 1.0, 11),
np.linspace(0.0, 1.0, 11),
cell_type="quad4", # or "quad8", "quad9"
)
```
#### Regular polygon
|  |
|  |
|  |
|
| :---------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------: |
| `meshzoo.ngon(4, 8)` | `meshzoo.ngon(6, 8)` | `meshzoo.ngon(9, 8)` |
```python
import meshzoo
points, cells = meshzoo.ngon(5, 11)
```
#### Disk
|  |
|  |
|  |
|
| :---------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: |
| `meshzoo.disk(4, 8)` | `meshzoo.disk(6, 8)` | `meshzoo.disk(9, 8)` |
The disk meshes are inflations of regular polygons.
```python
import meshzoo
points, cells = meshzoo.disk(6, 11)
points, cells = meshzoo.disk_quad(10, cell_type="quad4") # or "quad8", "quad9"
```
#### Möbius strip
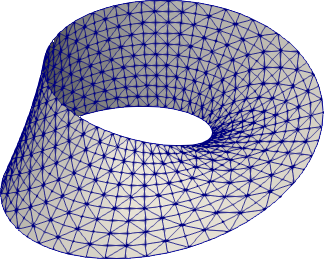
```python
import meshzoo
points, cells = meshzoo.moebius(num_twists=1, nl=60, nw=11)
```
#### Sphere (surface)
|  |
|  |
|
| :--------------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------------: |
```python
import meshzoo
points, cells = meshzoo.uv_sphere(num_points_per_circle=20, num_circles=10, radius=1.0)
points, tri, quad = meshzoo.geo_sphere(
num_points_per_circle=20, num_circles=10, radius=1.0
)
```
Spheres can also be generated by refining the faces of [platonic
solids](https://en.wikipedia.org/wiki/Platonic_solid) and then "inflating" them. meshzoo
implements a few of them. The sphere generated from the icosahedron has the
highest-quality (most equilateral) triangles.
All cells are oriented such that its normals point outwards.
|  |
|  |
|  |
|
| :-----------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------------: |
| `meshzoo.tetra_sphere(10)` | `meshzoo.octa_sphere(10)` | `meshzoo.icosa_sphere(10)` |
#### Ball (solid)
|  |
|  |
|
| :---------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: |
```python
import meshzoo
points, cells = meshzoo.ball_tetra(10)
points, cells = meshzoo.ball_hexa(10)
```
#### Tube

```python
import meshzoo
points, cells = meshzoo.tube(length=1.0, radius=1.0, n=30)
```
#### Cube
|  |
|  |
|
| :---------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: |
```python
import meshzoo
import numpy as np
points, cells = meshzoo.cube_tetra(
np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11)
)
points, cells = meshzoo.cube_hexa(
np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11)
)
```