Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.
Awesome Lists | Featured Topics | Projects
https://github.com/mothnik/robust_fourier

Noise- and Outlier-Robust Fourier Transform with Hermite Functions with NumPy and Numba
https://github.com/mothnik/robust_fourier
chebyshev-polynomials fourier-transform hermite-functions hermite-polynomials least-square-regression logsumexp numba numpy python robust-statistics
Last synced: 2 months ago
JSON representation
Noise- and Outlier-Robust Fourier Transform with Hermite Functions with NumPy and Numba
Host: GitHub
URL: https://github.com/mothnik/robust_fourier
Owner: MothNik
License: mit
Created: 2024-07-05T09:37:20.000Z (6 months ago)
Default Branch: main
Last Pushed: 2024-09-17T18:12:06.000Z (3 months ago)
Last Synced: 2024-09-29T00:23:16.415Z (3 months ago)
Topics: chebyshev-polynomials, fourier-transform, hermite-functions, hermite-polynomials, least-square-regression, logsumexp, numba, numpy, python, robust-statistics
Language: Python
Homepage:
Size: 28 MB
Stars: 1
Watchers: 1
Forks: 0
Open Issues: 3
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project

README

        # `robust_fourier`

[![python-3.9](https://img.shields.io/badge/python-3.9-blue.svg)](https://www.python.org/downloads/release/python-390/)

[![python-3.10](https://img.shields.io/badge/python-3.10-blue.svg)](https://www.python.org/downloads/release/python-3100/)

[![python-3.11](https://img.shields.io/badge/python-3.11-blue.svg)](https://www.python.org/downloads/release/python-3110/)

[![python-3.12](https://img.shields.io/badge/python-3.12-blue.svg)](https://www.python.org/downloads/release/python-3120/)

[![code style: black](https://img.shields.io/badge/code%20style-black-000000.svg)](https://github.com/psf/black)

[![code style: isort](https://img.shields.io/badge/code%20style-isort-000000.svg)](https://pycqa.github.io/isort/)

[![Checked with mypy](http://www.mypy-lang.org/static/mypy_badge.svg)](http://mypy-lang.org/)

[![codecov](https://codecov.io/gh/MothNik/robust_fourier/branch/10-improve-and-add-coverage-to-CI/graph/badge.svg)](https://codecov.io/gh/MothNik/robust_fourier/branch/10-improve-and-add-coverage-to-CI)

![tests](https://github.com/MothNik/robust_fourier/actions/workflows/python-package.yml/badge.svg)





You want to compute the Fourier transform of a signal, but your signal can be corrupted by outliers? If so, this package is for you even though you will have to say goodbye to the _"fast"_ in _Fast Fourier Transform_ 🏃🙅‍♀️

## 🎁 Installation

### 🐍☁️ PyPI

The package can be installed from PyPI with

```bash

pip install robust_fourier

```

If speed matters for you, you can also install the package with the optional dependency

`numba`

```bash

pip install robust_fourier[fast]

```

### 🐙📦 GitHub

To install the package from GitHub, you can simply clone the repository

```bash

git clone https://github.com/MothNik/robust_fourier.git

```

For the following commands, a `Makefile` is provided to simplify the process. Its use is

optional, but recommended.


From within the repositories root directory, the package can be installed for normal use

```bash

# ⚠️ first, activate your virtual environment, e.g., source venv/bin/activate

make install

# equivalent to

pip install --upgrade .

```

or for development (with all the development dependencies)

```bash

# ⚠️ first, activate your virtual environment, e.g., source venv/bin/activate

make install-dev

# equivalent to

pip install --upgrade .["dev"]

```

## ⚙️ Setup and 🪛 Development

When working in developer mode, an environment variable has to be added to run certain

scripts.

```

ROBFT_DEVELOPER = true

```

### 🔎 Code quality

The following checks for `black`, `isort`, `pyright`, `mypy`, `pycodestyle`, and

`ruff` - that are also part of the CI pipeline - can be run with

```bash

make black-check

make isort-check

make pyright-check

make mypy-check

make pycodestyle-check

make ruff-check

# or for all at once

make check

# equivalent to

black --check --diff --color ./auxiliary_scripts ./examples ./src ./tests

isort --check --diff --color ./auxiliary_scripts ./examples ./src ./tests

pyright ./auxiliary_scripts ./examples ./src ./tests

mypy ./auxiliary_scripts ./examples ./src ./tests

ruff check ./auxiliary_scripts ./examples ./src ./tests

pycodestyle ./auxiliary_scripts ./examples ./src ./tests --max-line-length=88 --ignore=E203,W503,E704

```

### ✅❌ Tests

To run the tests - almost like in the CI pipeline - you can use

```bash

make test-xmlcov  # for an XML report

make test-htmlcov  # for an HTML report

# equivalent to

pytest --cov=robust_fourier ./tests -n="auto" --cov-report=xml -x --no-jit

pytest --cov=robust_fourier ./tests -n="auto" --cov-report=html -x --no-jit

```

for parallelized testing whose coverage report will be stored in the file

`./coverage.xml` or in the folder `./htmlcov`, respectively.

## 〰️ Hermite functions

Being the eigenfunctions of the Fourier transform, Hermite functions are excellent

candidates for the basis functions for a Least Squares Regression approach to the Fourier

transform. However, their evaluation can be a bit tricky.

The module `hermite_functions` offers a numerically stable way to evaluate Hermite

functions or arbitrary order $n$ and argument - that can be scaled with a factor

$\alpha$ and shifted by a constant $\mu$:



  



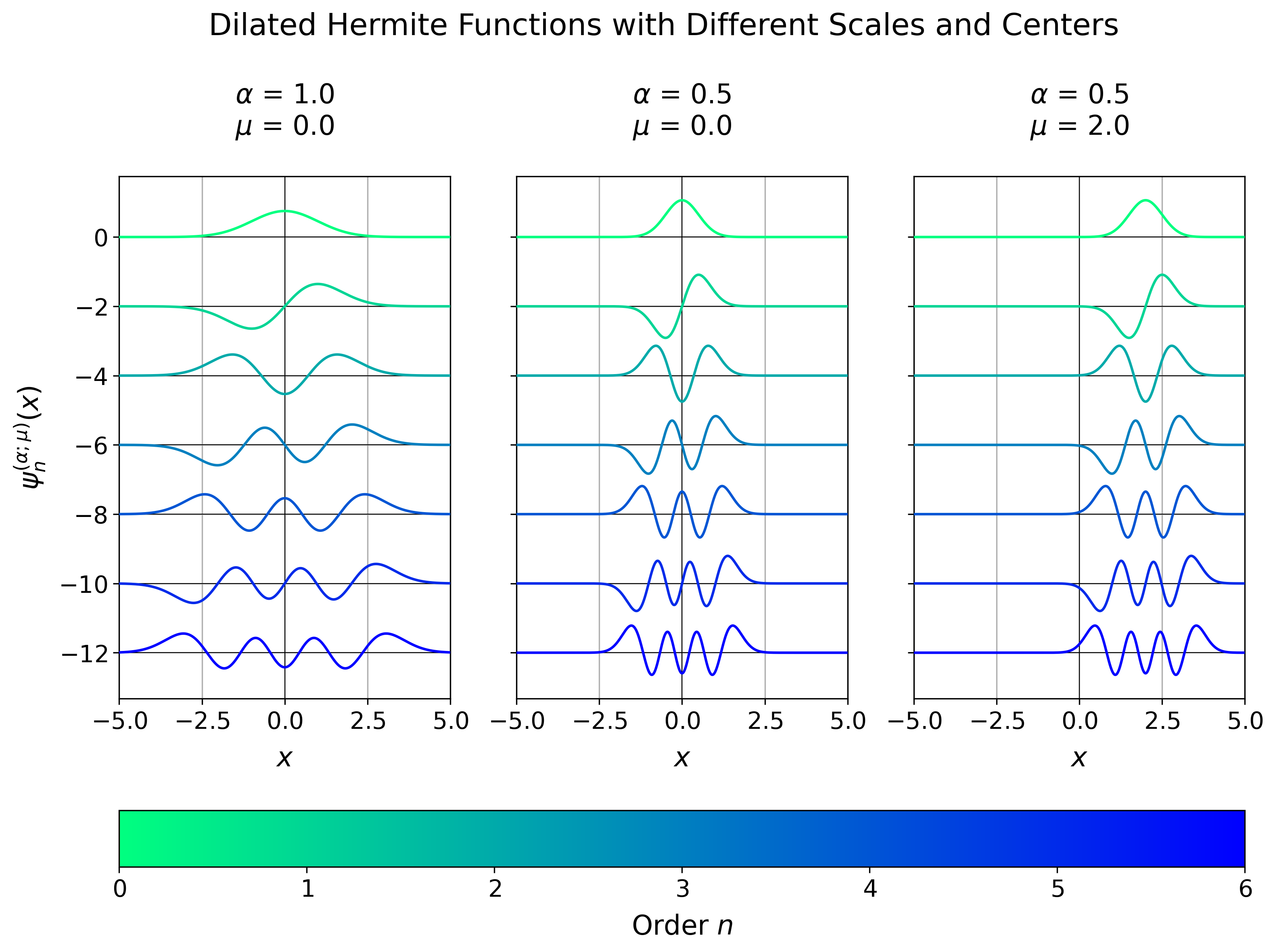
After a slight modification of the definitions in [[1]](#references), the Hermite

functions can be written as



  



with the Hermite polynomials



  



With `robust_fourier`, the Hermite functions can be evaluated for arbitrary orders

using the function interface `hermite_function_vander`

```python

import numpy as np

from robust_fourier import hermite_function_vander

ORDER_MAX = 25  # the maximum order of the Hermite functions

ALPHA = 2.0  # the scaling factor for the x-variable

MU = -2.0  # the shift of the x-variable

X_FROM = -20.0

X_TO = 20.0

NUM_X = 10_001

x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)

hermite_vander = hermite_function_vander(

    x=x_values,

    n=ORDER_MAX,

    alpha=ALPHA,

    x_center=MU,

    jit=True,  # will only take effect if Numba is installed

)

```

By making use of logarithm tricks, the evaluation that might involve infinitely high

polynomial values and at the same time infinitely small Gaussians - that are on top of

that scaled by an infinitely high factorial - can be computed safely and yield accurate

results.

For doing so, the relation between the dilated and the non-dilated Hermite functions



  



and the recurrence relation for the Hermite functions



  



are used, but not directly. Instead, the latest evaluated Hermite function is kept at a

value of either -1, 0, or +1 during the recursion and the logarithm of a correction

factor is tracked and applied when the respective Hermite function is finally evaluated

and stored. This approach is based on [[2]](#references).

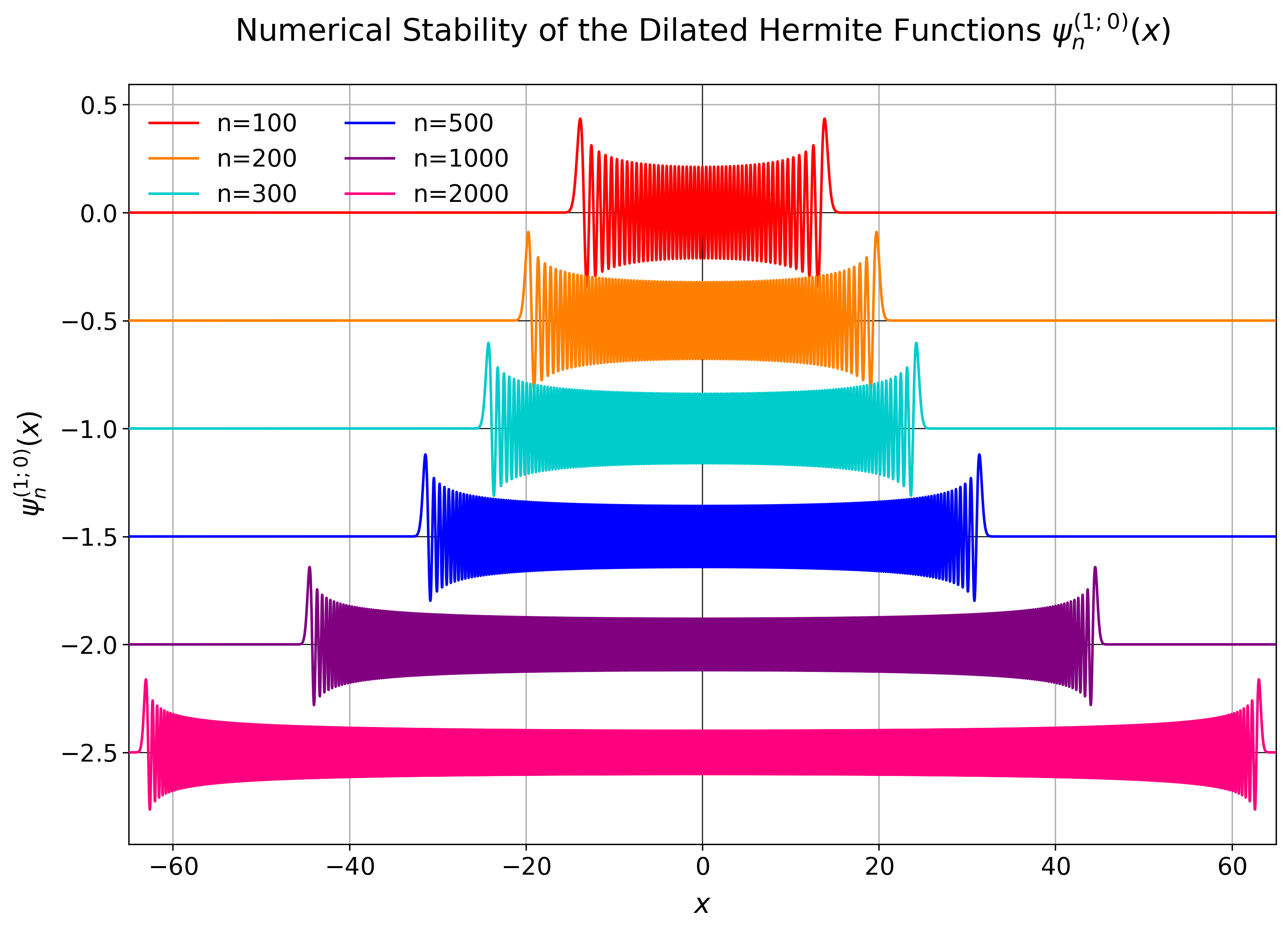
The implementation is tested against a symbolic evaluation with `sympy` that uses 200

digits of precision and it can be shown that even orders as high as 2,000 can still be

computed even though neither the polynomial, the Gaussian nor the factorial can be

evaluated for this anymore. The factorial for example would already have overflown for

orders of 170 in `float64`-precision.



  



As a sanity check, their orthogonality is part of the tests together with a test for

the fact that the absolute values of the Hermite functions for real input cannot exceed

the value $\frac{1}{\sqrt[4]{\pi\cdot\alpha^{2}}}$.

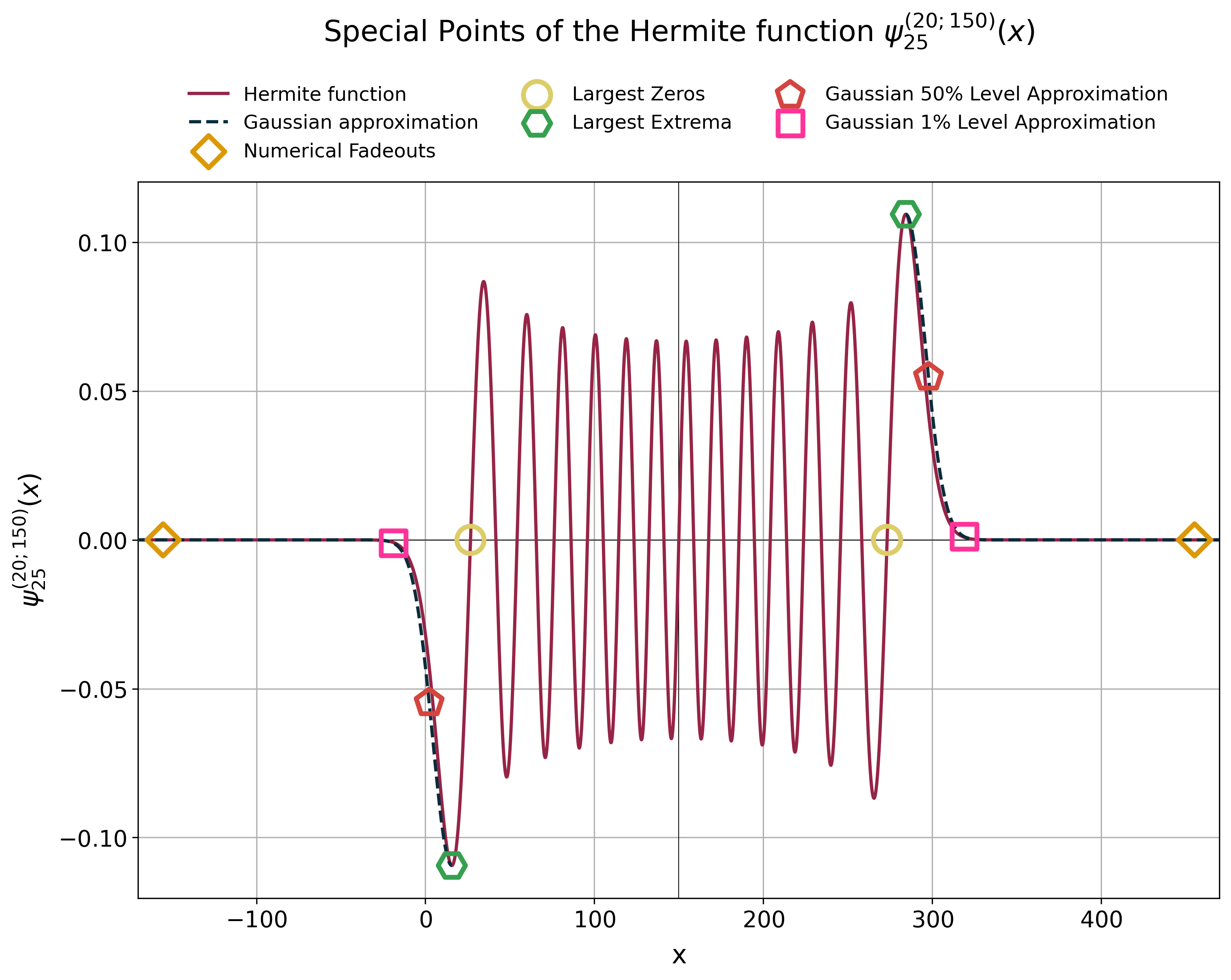
On top of that `robust_fourier` comes with utility functions to approximate some

special points of the Hermite functions, namely the x-positions of their

- largest root (= outermost zero),

- largest extrema in the outermost oscillation,

- the point where they numerically fade to zero, and

- an approximation of the outermost oscillation (tail) by a conservative Gaussian peak.

```python

import numpy as np

from robust_fourier import hermite_approx

ORDER = 25  # the order of the Hermite functions

ALPHA = 20.0  # the scaling factor for the x-variable

MU = 150.0  # the shift of the x-variable

X_FROM = -65.0

X_TO = 65.0

NUM_X = 100_001

# 1) the x-positions at which the outermost oscillation fades below machine

# precision

x_fadeout = hermite_approx.x_fadeout(

    n=ORDER,

    alpha=ALPHA,

    x_center=MU,

)

# 2) the x-positions of the largest zeros

x_largest_zero = hermite_approx.x_largest_zeros(

    n=ORDER,

    alpha=ALPHA,

    x_center=MU,

)

# 3) the x-positions of the largest extrema

x_largest_extremum = hermite_approx.x_largest_extrema(

    n=ORDER,

    alpha=ALPHA,

    x_center=MU,

)

# 4) the Gaussian approximation of the outermost oscillation ...

left_gaussian, right_gaussian = hermite_approx.get_tail_gauss_fit(

    n=ORDER,

    alpha=ALPHA,

    x_center=MU,

)

# ... which is solved for the 50% level

x_left_fifty_percent = left_gaussian.solve_for_y_fraction(y_fraction=0.5)

x_right_fifty_percent = right_gaussian.solve_for_y_fraction(y_fraction=0.5)

# ... but can also be evaluated for all x-values

x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)

left_gaussian_values = left_gaussian(x=x_values)

right_gaussian_values = right_gaussian(x=x_values)

# 5) the Gaussian approximation is also solved for the 1% interval as a more

# realistic (less conservative) approximation of the fadeout point

x_one_percent = hermite_approx.x_tail_drop_to_fraction(

    n=ORDER,

    y_fraction=0.01,

    alpha=ALPHA,

    x_center=MU,

).ravel()

```



  



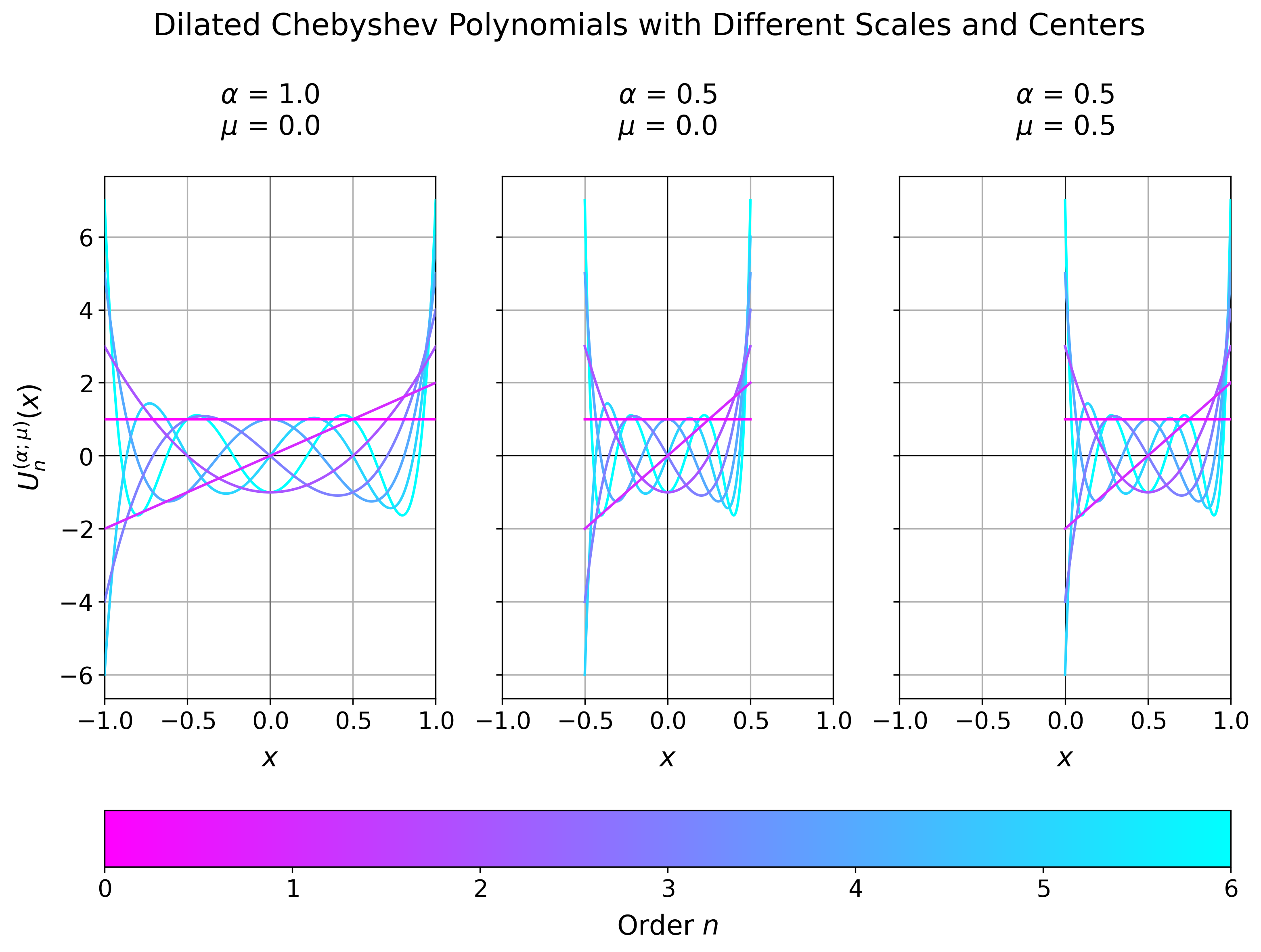
## 🧮 Chebyshev Polynomials

Even though the [Hermite functions](#〰️-hermite-functions) have some nice properties,

they are not necessarily the best choice for the Fourier transform. Choosing their

scaling parameter $\alpha$ can be a bit tricky.

Therefore [[3]](#references) suggests using Chebyshev polynomials instead. They are

only defined on the interval $[-1, 1]$ and can be scaled and shifted to fit the

interval $[\mu - \alpha, \mu + \alpha]$ like



  

for the first kind and



  

for the second kind. In [[3]](#references) the second kind $U$ is used, but the first

kind $T$ is also implemented in `robust_fourier`

```python

import numpy as np

from robust_fourier import chebyshev_polyvander

ORDER_MAX = 10  # the maximum order of the Chebyshev polynomials

ALPHA = 0.5  # the scaling factor for the x-variable

MU = 0.5  # the shift of the x-variable

X_FROM = -0.5

X_TO = 0.5

NUM_X = 10_001

x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)

chebyshev_vander_first_kind = chebyshev_polyvander(

    x=x_values,

    n=ORDER_MAX,

    alpha=ALPHA,

    x_center=MU,

    kind="first",

    jit=True,  # will only take effect if Numba is installed

)

chebyshev_vander_second_kind = chebyshev_polyvander(

    x=x_values,

    n=ORDER_MAX,

    alpha=ALPHA,

    x_center=MU,

    kind="second",

    jit=True,  # will only take effect if Numba is installed

)

# alternatively, both kinds can be computed in one go because this is how they are

# computed internally to achieve maximum accuracy

(

  chebyshev_vander_first_kind,

  chebyshev_vander_second_kind,

) = chebyshev_polyvander(

    x=x_values,

    n=ORDER_MAX,

    alpha=ALPHA,

    x_center=MU,

    kind="both",

    jit=True,  # will only take effect if Numba is installed

)

```



  



## 📈 Fourier Transform

🏗️🚧 👷👷‍♂️👷‍♀️🏗️🚧

Currently under construction. Please check back later.

## 🙏 Acknowledgements

This package would not have been possible without the - unfortunately apparently

abandoned - package [`hermite-functions`](https://github.com/Rob217/hermite-functions)

which was a great inspiration for the implementation of the Hermite functions.

On top of that, I hereby want to thank the anonymous support that patiently listened to

my endless talks about the greatness of Hermite functions (even though they cannot keep

up with her) and that also helped me to give the plots the visual appeal they have now

🤩.

## 📖 References

- [1] Dobróka M., Szegedi H., and Vass P., Inversion-Based Fourier Transform as a New

  Tool for Noise Rejection, _Fourier Transforms - High-tech Application and Current Trends_

  (2017), DOI: [http://dx.doi.org/10.5772/66338](http://dx.doi.org/10.5772/66338)

- [2] Bunck B. F., A fast algorithm for evaluation of normalized Hermite functions,

  _BIT Numer Math_ (2009), 49, pp. 281–295, DOI:

  [https://doi.org/10.1007/s10543-009-0216-1](https://doi.org/10.1007/s10543-009-0216-1)

- [3] Al Marashly, O., Dobróka, M., Chebyshev polynomial-based Fourier transformation

  and its use in low pass filter of gravity data, _Acta Geod Geophys_ (2024), 59,

  pp. 159–181 DOI: [https://doi.org/10.1007/s40328-024-00444-z](https://doi.org/10.1007/s40328-024-00444-z)

- [4] Hrycak T., Schmutzhard S., Accurate evaluation of Chebyshev polynomials in

  floating-point arithmetic, _BIT Numer Math_ (2019), 59, pp. 403–416,

  DOI: [https://doi.org/10.1007/s10543-018-0738-5](https://doi.org/10.1007/s10543-018-0738-5)