Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/mschauer/Kalman.jl

Flexible filtering and smoothing in Julia
https://github.com/mschauer/Kalman.jl

filter kalman-filter kalman-smoother tracking

Last synced: 3 months ago
JSON representation

Flexible filtering and smoothing in Julia

Awesome Lists containing this project

README 

        
[![Build Status](https://travis-ci.org/mschauer/Kalman.jl.svg?branch=master)](https://travis-ci.org/mschauer/Kalman.jl)



[![Latest](https://img.shields.io/badge/docs-latest-blue.svg)](https://mschauer.github.io/Kalman.jl/latest/)



# Kalman

Flexible filtering and smoothing in Julia. `Kalman` uses [`DynamicIterators`](https://github.com/mschauer/DynamicIterators.jl) (an iterator protocol for dynamic data dependent and controlled processes) and

[`GaussianDistributions`](https://github.com/mschauer/GaussianDistributions.jl) (Gaussian distributions as abstraction for the uncertain state)

to implement flexible online Kalman filtering.



The package provides tools to filter and smooth and conditionally sample the state space system



    x[k] = Φx[k−1] + b + w[k],    w[k] ∼ N(0, Q)



    y[k] = Hx[k] + v[k],    v[k] ∼ N(0, R)



## How to use

One way, and maybe *the* way, to use this package is to use `Gaussian` from `GaussianDistributions.jl` as representation of mean and uncertainty of a filter and call `Kalman.correct` to implement the correction step in a Kalman filter:

```julia

using Kalman, GaussianDistributions, LinearAlgebra

using GaussianDistributions: ⊕ # independent sum of Gaussian r.v.

using Statistics



# prior for time 0

x0 = [-1., 1.]

P0 = Matrix(1.0I, 2, 2)



# dynamics

Φ = [0.8 0.2; -0.1 0.8]

b = zeros(2)

Q = [0.2 0.0; 0.0 0.5]



# observation

H = [1.0 0.0]

R = Matrix(0.3I, 1, 1)



# (mock) data

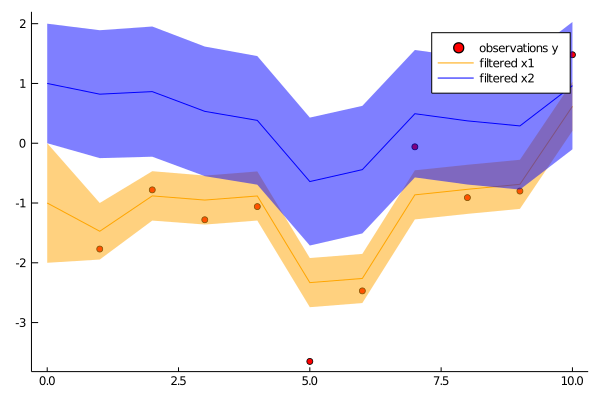
ys = [[-1.77], [-0.78], [-1.28], [-1.06], [-3.65], [-2.47], [-0.06], [-0.91], [-0.80], [1.48]]



# filter (assuming first observation at time 1)

N = length(ys)



p = Gaussian(x0, P0)

ps = [p] # vector of filtered Gaussians

for i in 1:N

    global p

    # predict

    p = Φ*p ⊕ Gaussian(zero(x0), Q) #same as Gaussian(Φ*p.μ, Φ*p.Σ*Φ' + Q)

    # correct

    p, yres, _ = Kalman.correct(Kalman.JosephForm(), p, (Gaussian(ys[i], R), H))

    push!(ps, p) # save filtered density

end



using Plots



p1 = scatter(1:N, first.(ys), color="red", label="observations y")

plot!(p1, 0:N, [mean(p)[1] for p in ps], color="orange", label="filtered x1", grid=false, ribbon=[sqrt(cov(p)[1,1]) for p in ps], fillalpha=.5)

plot!(p1, 0:N, [mean(p)[2] for p in ps], color="blue", label="filtered x2", grid=false, ribbon=[sqrt(cov(p)[2,2]) for p in ps], fillalpha=.5)



savefig(p1, "filter.png")

```



![Filtered trajectory with uncertainty](https://raw.githubusercontent.com/mschauer/Kalman.jl/master/filter.png)



A very similar example of tracking a 2D trajectory can be found [here](example/trajectory_tracking/kalman.jl).



## Interface



The same might be achieved using interface functions



```julia

using DynamicIterators, GaussianDistributions, Kalman, LinearAlgebra



# Define linear evolution

Φ = [0.8 0.5; -0.1 0.8]

b = zeros(2)

Q = [0.2 0.0; 0.0 1.0]



E = LinearEvolution(Φ, Gaussian(b, Q))



# Define observation scheme

H = [1.0 0.0]

R = Matrix(1.0I, 1, 1)



O = LinearObservation(E, H, R)



# Prior

x0 = [1., 0.]

P0 = Matrix(1.0I, 2, 2)



# Observations (mock)

Y = [1 => [1.14326], 2 => [-0.271804], 3 => [-0.00512675]]



# Filter

Xf, ll = kalmanfilter(O, 0 => Gaussian(x0, P0), Y)

@show Xf



```



## Implementation

As said, filtering is implemented via the DynamicIterator protocol. It is worthwhile to look at

a possible the implementation of `kalmanfilter` to see how filtering can be integrated into online algorithms (run in a local scope to avoid `UndefVarError: ystate not defined`.)



```julia

# `Y` is the data iterator, iterating over pairs of  `t => v` of time `t` and observation `v`

# `O` is the dynamical filter iterator, iterating over pairs `t => u` where

#     u::Tuple{<:Gaussian,<:Gaussian,Float64}

# is the tuple of filtered state, the predicted state and the log likelihood



# Initialise data iterator



ϕ = iterate(Y)

ϕ === nothing && error("no observations")

(t, v), ystate = ϕ



# Initialise dynamical filter with first data point `t => v`

# and the `prior::Pair{Int,<:Gaussian}`, a pair of initial time and initial state

prior = 0 => Gaussian(x0, P0)



ϕ = dyniterate(O, Start(Kalman.Filter(prior, 0.0)), t => v)

ϕ === nothing && error("no observations")

(t, u), state = ϕ



X = [t => u[1]]

while true



    # Advance data iterator

    

    ϕ = iterate(Y, ystate)

    ϕ === nothing && break

    (t, v), ystate = ϕ



    # Advance filter with new data `t => v`

    

    ϕ = dyniterate(O, state, t => v)

    ϕ === nothing && break

    (t, u), state = ϕ

    

    # Do something with the result `t => u` (here: saving it)

    

    push!(X, t => u[1]) # save filtered state

end

ll = u[3] # likelihood

@show  X, ll

```