Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.
Awesome Lists | Featured Topics | Projects
https://github.com/nschloe/cplot

:rainbow: Plot complex functions
https://github.com/nschloe/cplot
mathematics matplotlib plotting python science
Last synced: 3 days ago
JSON representation
:rainbow: Plot complex functions
Host: GitHub
URL: https://github.com/nschloe/cplot
Owner: nschloe
License: gpl-3.0
Created: 2018-01-24T09:55:51.000Z (almost 7 years ago)
Default Branch: main
Last Pushed: 2023-11-25T19:14:09.000Z (about 1 year ago)
Last Synced: 2025-01-14T06:07:27.547Z (10 days ago)
Topics: mathematics, matplotlib, plotting, python, science
Language: Python
Homepage:
Size: 75.1 MB
Stars: 155
Watchers: 8
Forks: 21
Open Issues: 7
Metadata Files:
- Readme: README.md
- License: LICENSE
- Citation: CITATION.cff
Awesome Lists containing this project

README

        


  

  
Plot complex-valued functions with style.


[![PyPi Version](https://img.shields.io/pypi/v/cplot.svg?style=flat-square)](https://pypi.org/project/cplot)

[![PyPI pyversions](https://img.shields.io/pypi/pyversions/cplot.svg?style=flat-square)](https://pypi.org/pypi/cplot/)

[![DOI](https://zenodo.org/badge/DOI/10.5281/zenodo.5599493.svg?style=flat-square)](https://doi.org/10.5281/zenodo.5599493)

[![GitHub stars](https://img.shields.io/github/stars/nschloe/cplot.svg?style=flat-square&logo=github&label=Stars&logoColor=white)](https://github.com/nschloe/cplot)

[![Downloads](https://pepy.tech/badge/cplot/month)](https://pepy.tech/project/cplot)

[![Discord](https://img.shields.io/static/v1?logo=discord&logoColor=white&label=chat&message=on%20discord&color=7289da&style=flat-square)](https://discord.gg/hnTJ5MRX2Y)

[![gh-actions](https://img.shields.io/github/workflow/status/nschloe/cplot/ci?style=flat-square)](https://github.com/nschloe/cplot/actions?query=workflow%3Aci)

[![codecov](https://img.shields.io/codecov/c/github/nschloe/cplot.svg?style=flat-square)](https://codecov.io/gh/nschloe/cplot)

[![Code style: black](https://img.shields.io/badge/code%20style-black-000000.svg?style=flat-square)](https://github.com/psf/black)

cplot helps plotting complex-valued functions in a visually appealing manner.

Install with

```

pip install cplot

```

and use as

```python

import numpy as np

import cplot

def f(z):

    return np.sin(z**3) / z

plt = cplot.plot(

    f,

    (-2.0, +2.0, 400),

    (-2.0, +2.0, 400),

    # abs_scaling=lambda x: x / (x + 1),  # how to scale the lightness in domain coloring

    # contours_abs=2.0,

    # contours_arg=(-np.pi / 2, 0, np.pi / 2, np.pi),

    # emphasize_abs_contour_1: bool = True,

    # add_colorbars: bool = True,

    # add_axes_labels: bool = True,

    # saturation_adjustment: float = 1.28,

    # min_contour_length = None,

    # linewidth = None,

)

plt.show()

```

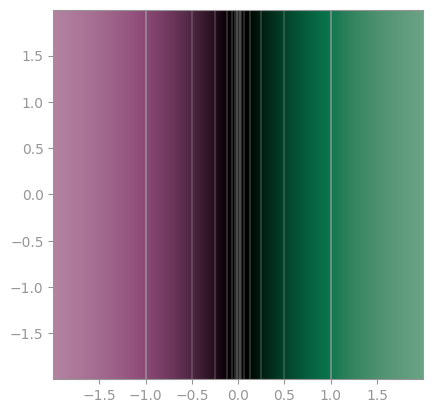
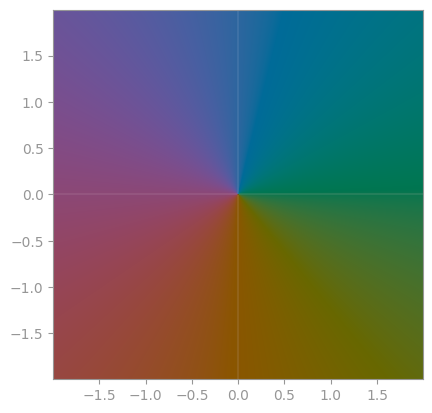
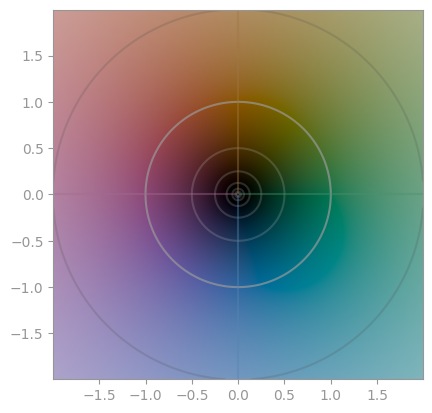
Historically, plotting of complex functions was in one of three ways

|  |  |  |

| :--------------------------------------------------------------------: | :--------------------------------------------------------------------: | :-------------------------------------------------------------------------: |

|          Only show the absolute value; sometimes as a 3D plot          |   Only show the phase/the argument in a color wheel (phase portrait)   |                   Show contour lines for both arg and abs                   |

Combining all three of them gives you a _cplot_:



  



See also [Wikipedia: Domain coloring](https://en.wikipedia.org/wiki/Domain_coloring).

Features of this software:

- cplot uses [OKLAB](https://bottosson.github.io/posts/oklab/), a perceptually

  uniform color space for the argument colors.

  This avoids streaks of colors occurring with other color spaces, e.g., HSL.

- The contour `abs(z) == 1` is emphasized, other abs contours are at 2, 4, 8, etc. and

  1/2, 1/4, 1/8, etc., respectively. This makes it easy to tell the absolte value

  precisely.

- For `arg(z) == 0`, the color is green, for `arg(z) == pi/2` it's blue, for `arg(z) = -pi / 2` it's orange, and for `arg(z) = pi` it's pink.

Other useful functions:

```python

# There is a tripcolor function as well for triangulated 2D domains

cplot.tripcolor(triang, z)

# The function get_srgb1 returns the SRGB1 triple for every complex input value.

# (Accepts arrays, too.)

z = 2 + 5j

val = cplot.get_srgb1(z)

```

#### Riemann sphere



  



cplot can also plot functions on the [Riemann

sphere](https://en.wikipedia.org/wiki/Riemann_sphere), a mapping of the complex

plane to the unit ball.

```python

import cplot

import numpy as np

cplot.riemann_sphere(np.log)

```

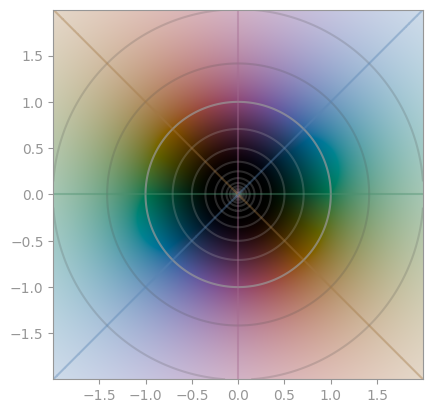
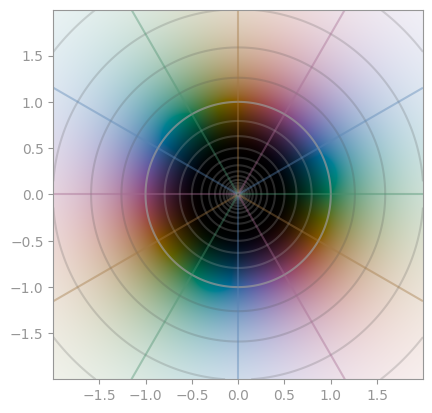
#### Gallery

All plots are created with default settings.

|  |  |  |

| :------------------------------------------------------------: | :------------------------------------------------------------: | :------------------------------------------------------------: |

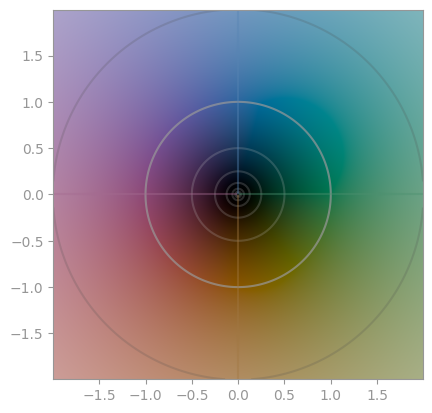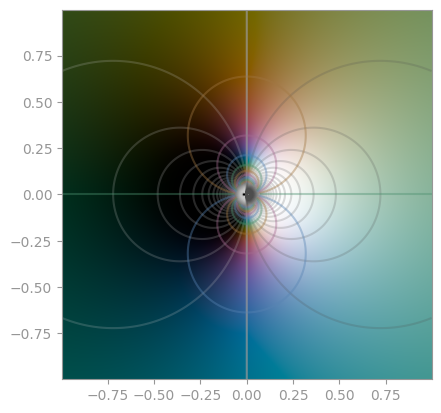
|                            `z ** 1`                            |                            `z ** 2`                            |                            `z ** 3`                            |

Many more plots

|  |  |  |

| :------------------------------------------------------------: | :-------------------------------------------------------------: | :-------------------------------------------------------------: |

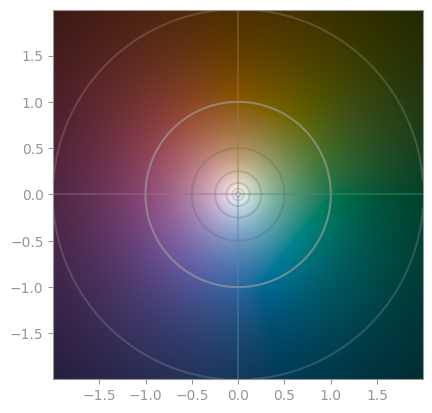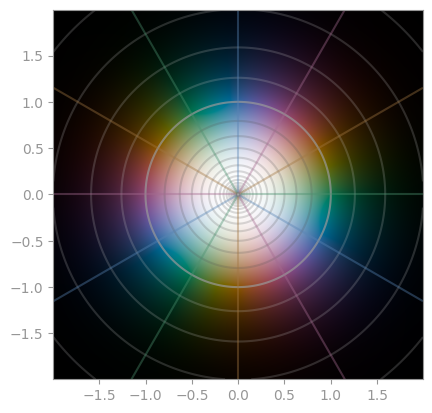|                            `1 / z`                             |                          `1 / z ** 2`                           |                          `1 / z ** 3`                           |

|  |                       |  |

| :------------------------------------------------------------------: | :---------------------------------------------------------------------------------------: | :------------------------------------------------------------------: |

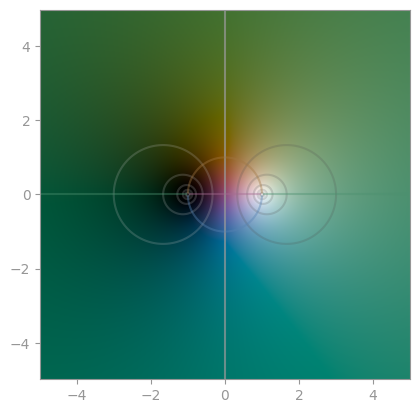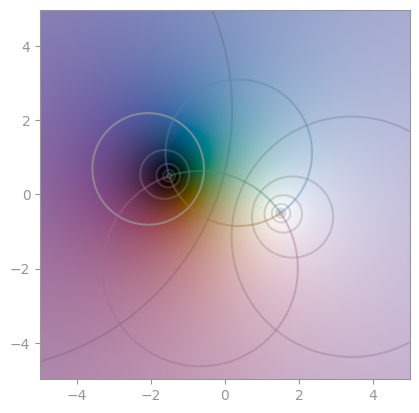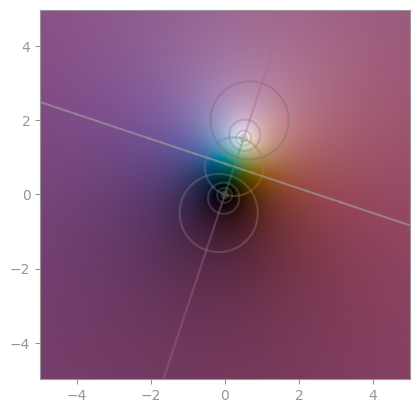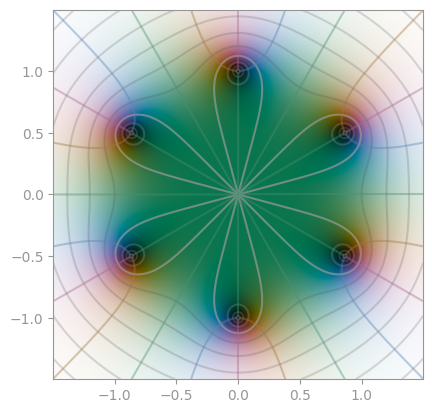
|                         `(z + 1) / (z - 1)`                          | Another [Möbius transformation](https://en.wikipedia.org/wiki/M%C3%B6bius_transformation) |                    A third Möbius transformation                     |

|  |  |  |

| :------------------------------------------------------------: | :----------------------------------------------------------------: | :--------------------------------------------------------------: |

|                           `np.real`                            |                            `z / abs(z)`                            |                            `np.conj`                             |

|  |  |  |

| :--------------------------------------------------------------: | :--------------------------------------------------------------: | :---------------------------------------------------------------: |

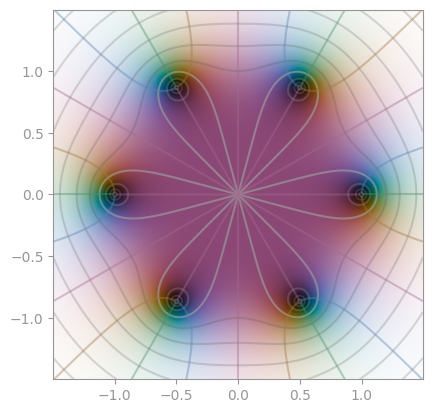
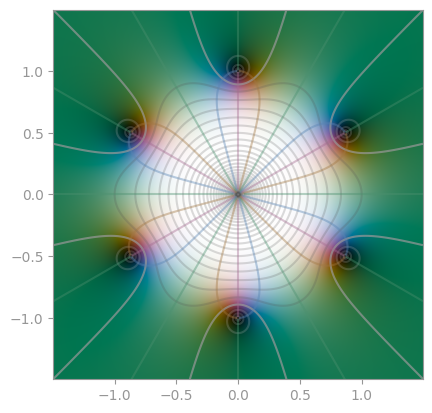
|                           `z ** 6 + 1`                           |   [`z ** 6 - 1`](https://en.wikipedia.org/wiki/Root_of_unity)    |                          `z ** (-6) + 1`                          |

|  |  |  |

| :------------------------------------------------------------: | :-------------------------------------------------------------: | :-------------------------------------------------------------: |

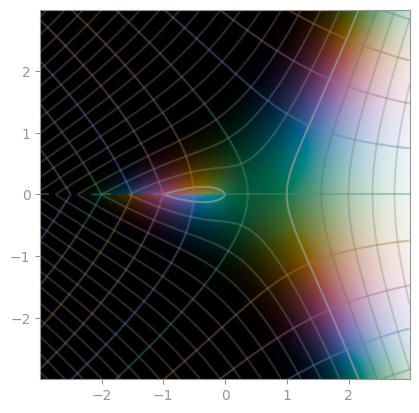
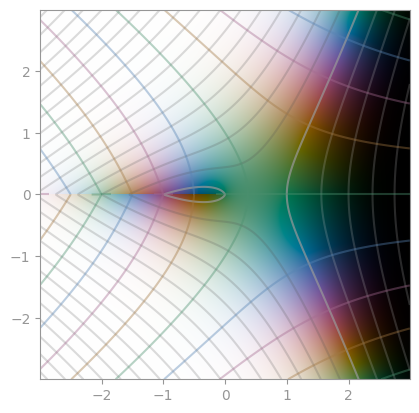
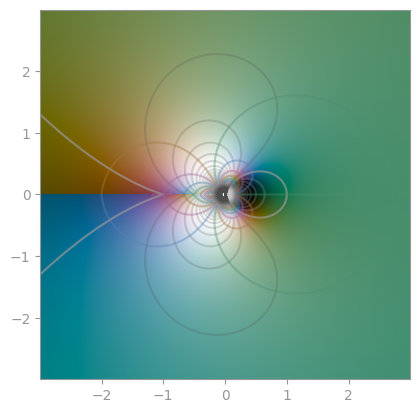
|                            `z ** z`                            |                          `(1/z) ** z`                           |                          `z ** (1/z)`                           |

|  |  |  |

| :---------------------------------------------------------------: | :---------------------------------------------------------------: | :---------------------------------------------------------------: |

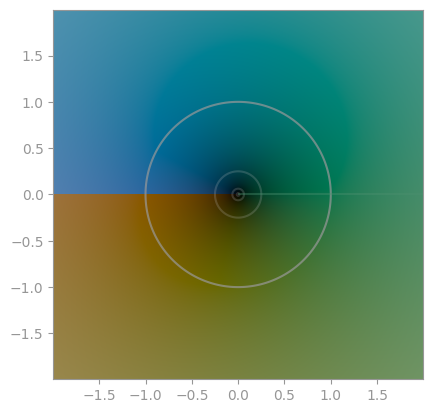
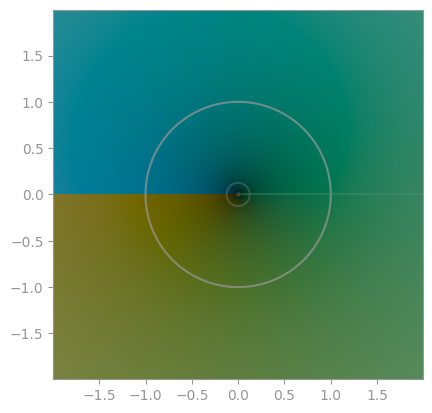
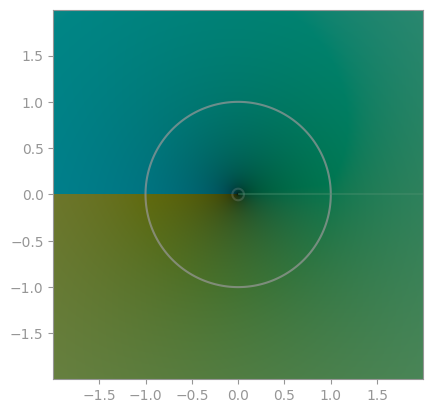
|                             `np.sqrt`                             |                            `z**(1/3)`                             |                            `z**(1/4)`                             |

|  |  |  |

| :-------------------------------------------------------------: | :-------------------------------------------------------------: | :--------------------------------------------------------------: |

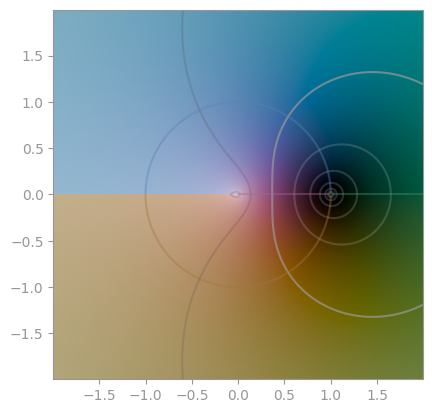
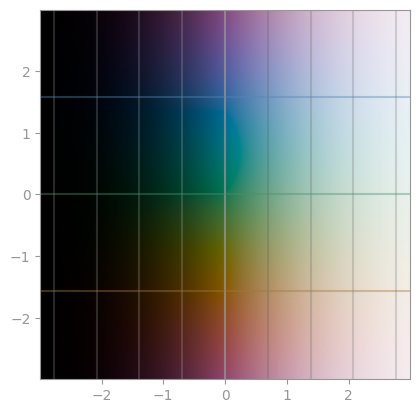
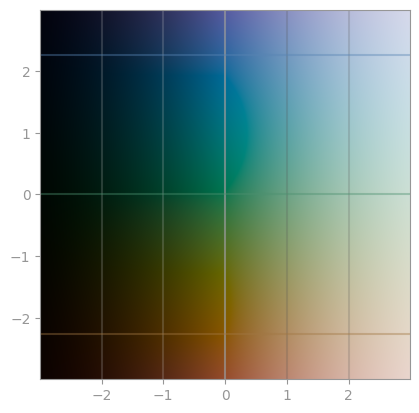
|       [`np.log`](https://en.wikipedia.org/wiki/Logarithm)       |                            `np.exp`                             |                            `np.exp2`                             |

|  |  |  |

| :---------------------------------------------------------------: | :----------------------------------------------------------------: | :---------------------------------------------------------------: |

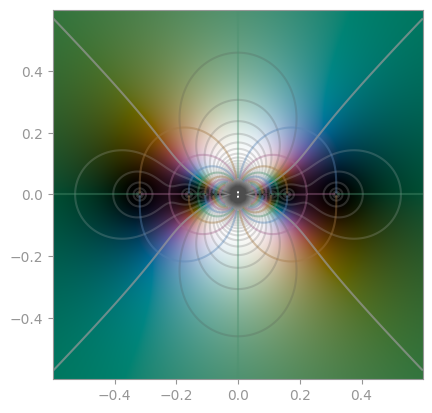
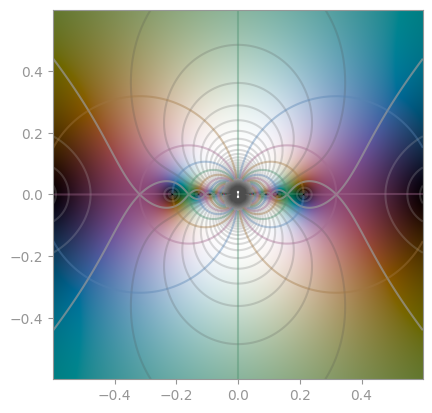
|                          `np.exp(1 / z)`                          |                        `z * np.sin(1 / z)`                         |                          `np.cos(1 / z)`                          |

|  |          |  |

| :----------------------------------------------------------------: | :----------------------------------------------------------------------: | :-------------------------------------------------------------: |

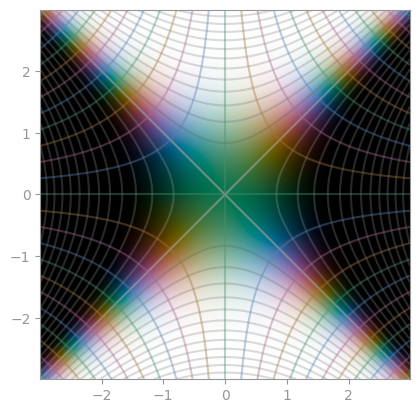
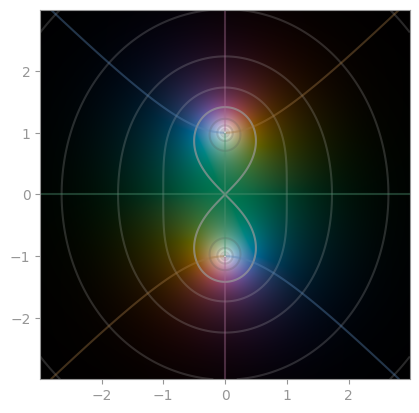
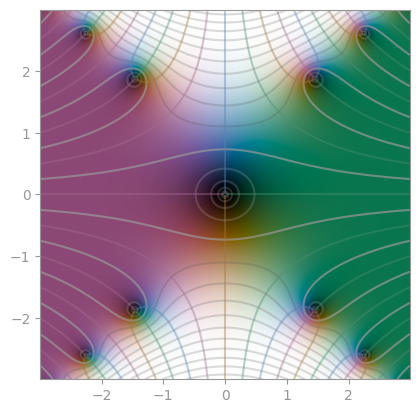
|                          `exp(- z ** 2)`                           | [`1 / (1 + z ** 2)`](https://en.wikipedia.org/wiki/Runge%27s_phenomenon) | [Error function](https://en.wikipedia.org/wiki/Error_function)  |

|  |  |  |

| :-------------------------------------------------------------: | :-------------------------------------------------------------: | :-------------------------------------------------------------: |

|                            `np.sin`                             |                            `np.cos`                             |                            `np.tan`                             |

|  |  |  |

| :-------------------------------------------------------------: | :-------------------------------------------------------------: | :-------------------------------------------------------------: |

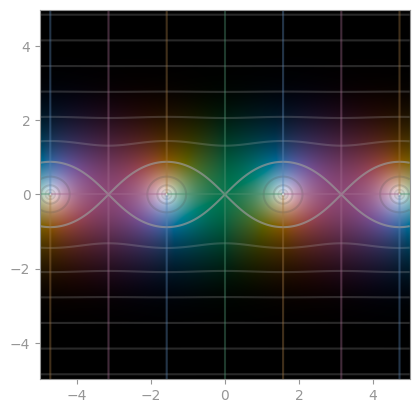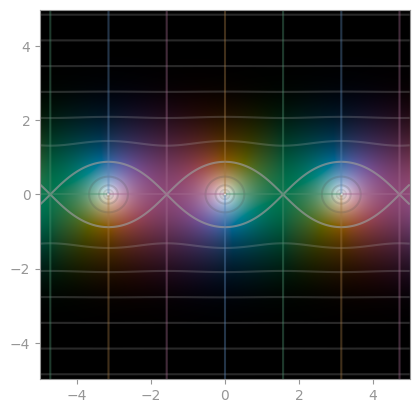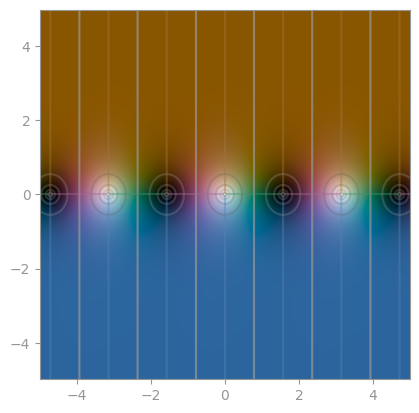|                              `sec`                              |                              `csc`                              |                              `cot`                              |

|  |  |  |

| :--------------------------------------------------------------: | :--------------------------------------------------------------: | :--------------------------------------------------------------: |

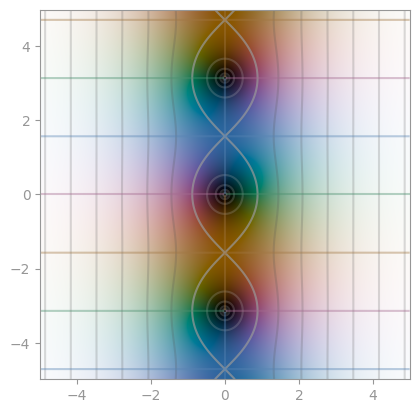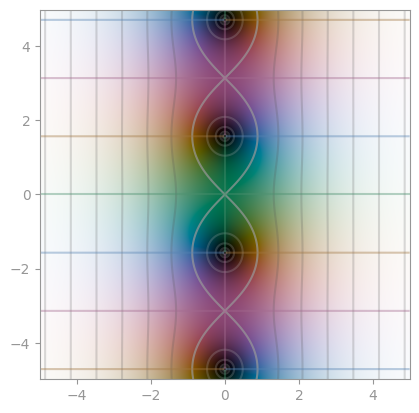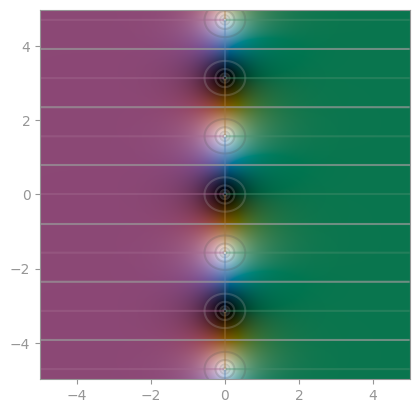| [`np.sinh`](https://en.wikipedia.org/wiki/Hyperbolic_functions)  |                            `np.cosh`                             |                            `np.tanh`                             |

|  |  |  |

| :--------------------------------------------------------------: | :--------------------------------------------------------------: | :--------------------------------------------------------------: |

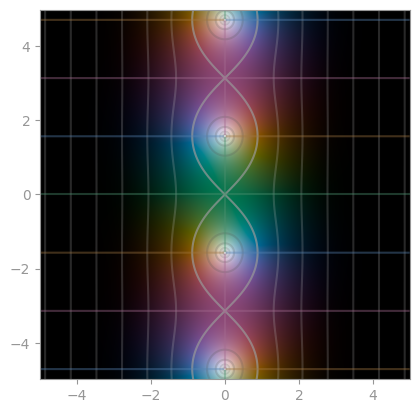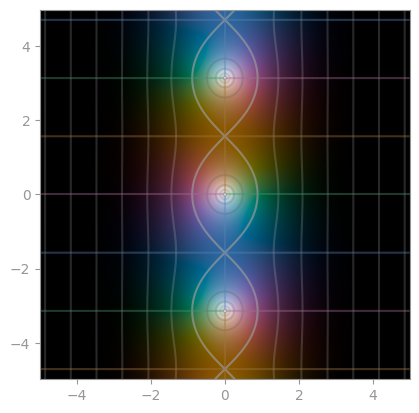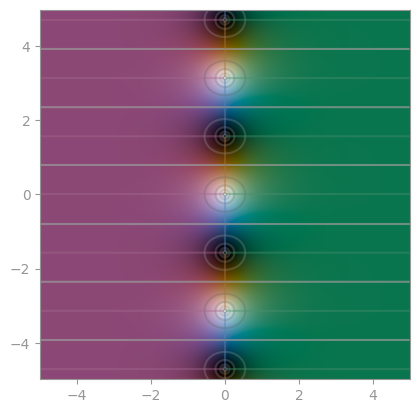
|                       secans hyperbolicus                        |                      cosecans hyperbolicus                       |                      cotangent hyperbolicus                      |

|  |  |  |

| :----------------------------------------------------------------: | :----------------------------------------------------------------: | :----------------------------------------------------------------: |

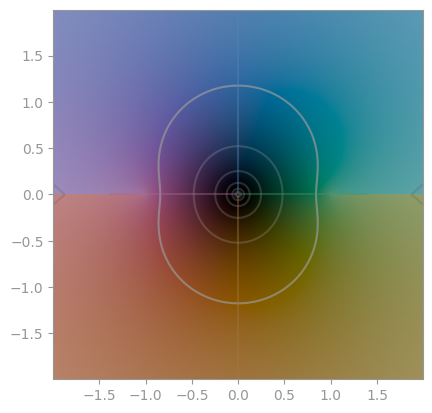
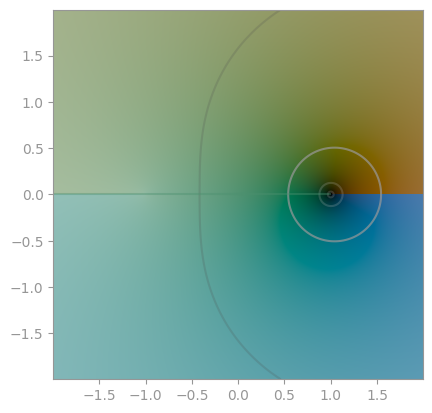
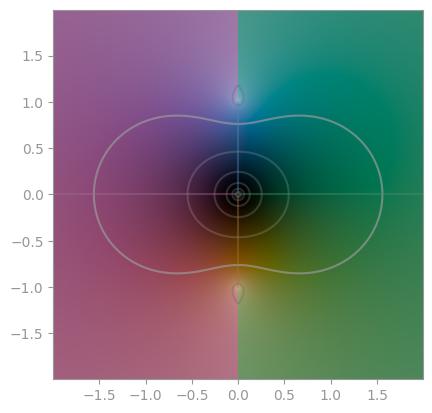
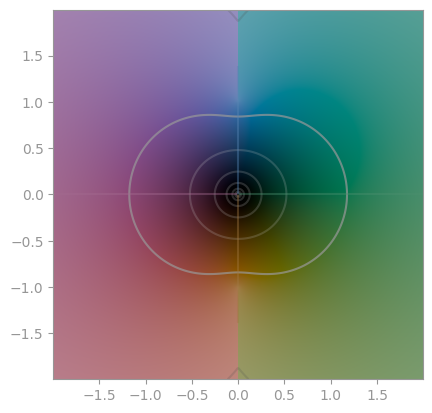
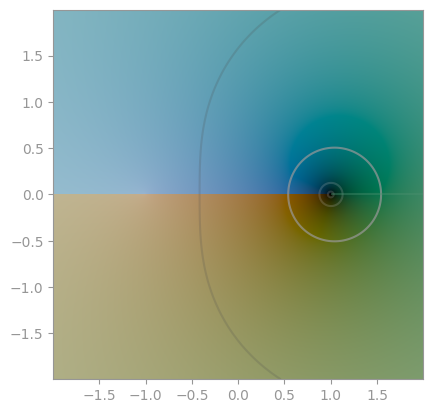
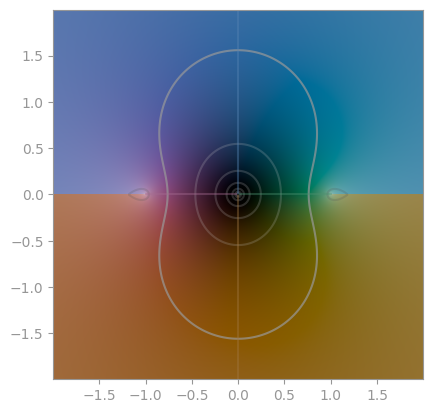
|                            `np.arcsin`                             |                            `np.arccos`                             |                            `np.arctan`                             |

|  |  |  |

| :-----------------------------------------------------------------: | :-----------------------------------------------------------------: | :-----------------------------------------------------------------: |

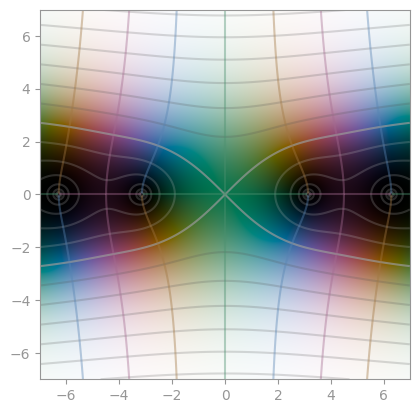
|                            `np.arcsinh`                             |                            `np.arccosh`                             |                            `np.arctanh`                             |

|  |  |  |

| :----------------------------------------------------------------: | :----------------------------------------------------------------: | :----------------------------------------------------------------: |

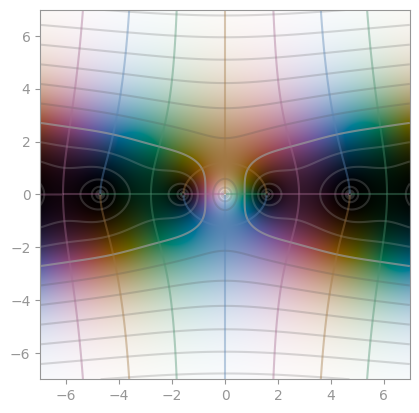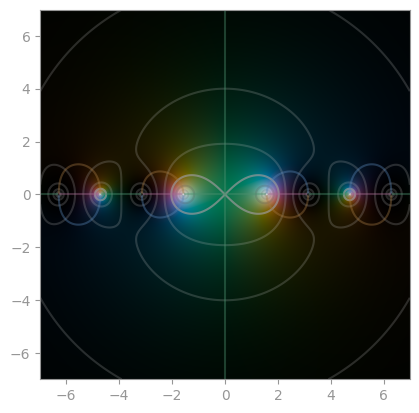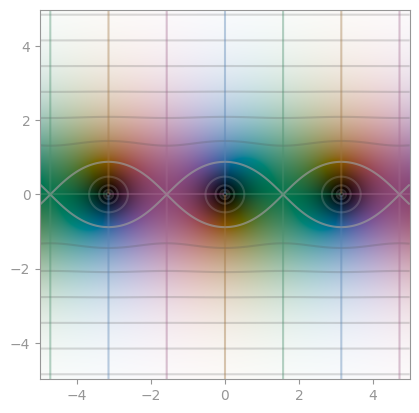
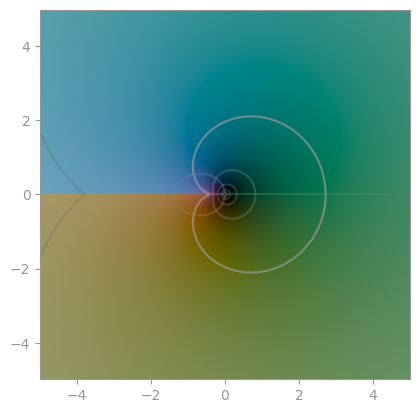
| [Sinc, `sin(z) / z`](https://en.wikipedia.org/wiki/Sinc_function)  |                            `cos(z) / z`                            |                            `tan(z) / z`                            |

|              |  |    |

| :------------------------------------------------------------------------: | :------------------------------------------------------------: | :--------------------------------------------------------------------: |

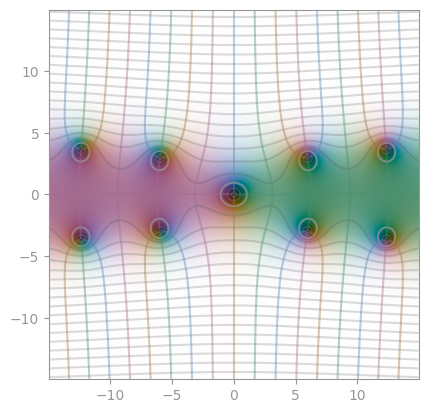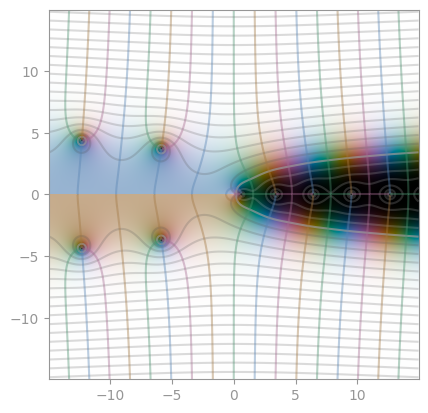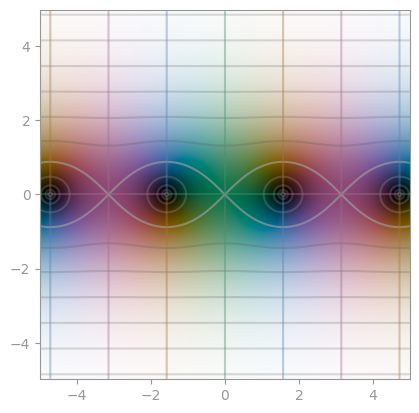
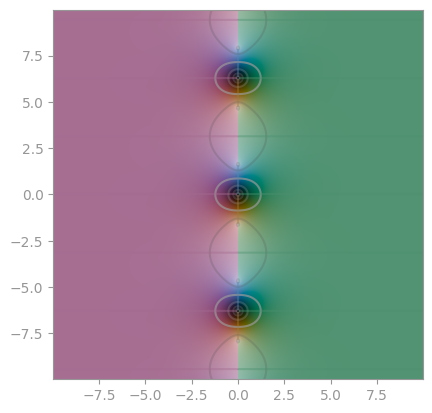
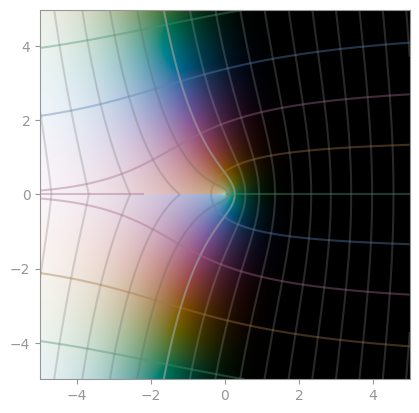
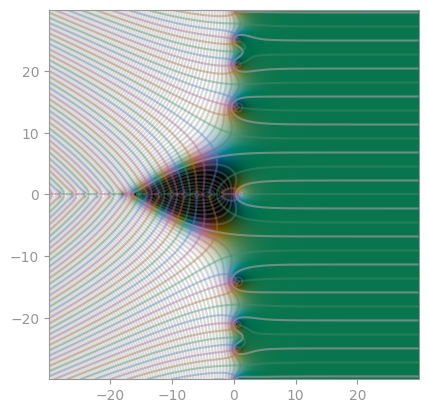
| [Integral sine _Si_](https://en.wikipedia.org/wiki/Trigonometric_integral) |                      Integral cosine _Ci_                      | [Lambert W function](https://en.wikipedia.org/wiki/Lambert_W_function) |

|      |  |  |

| :--------------------------------------------------------------------------: | :--------------------------------------------------------------: | :--------------------------------------------------------------: |

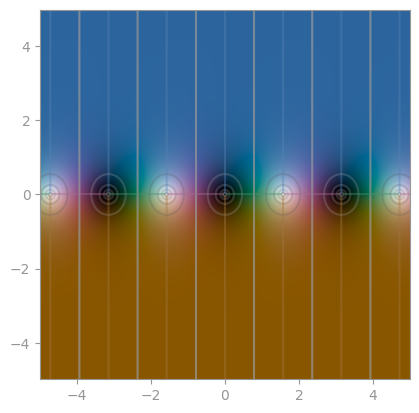
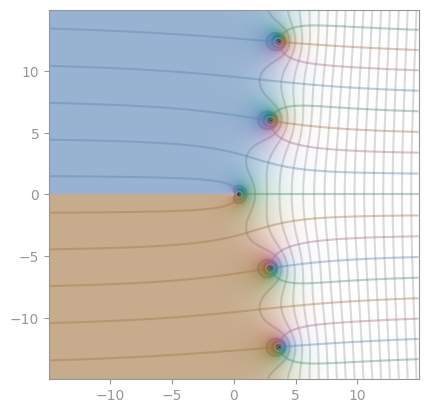
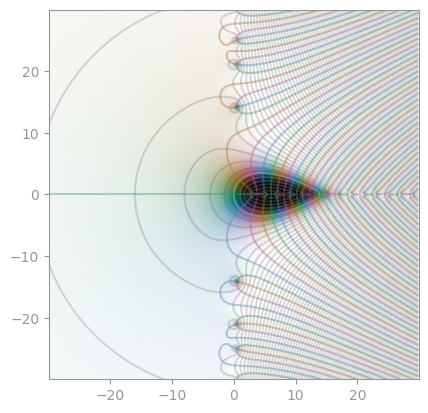
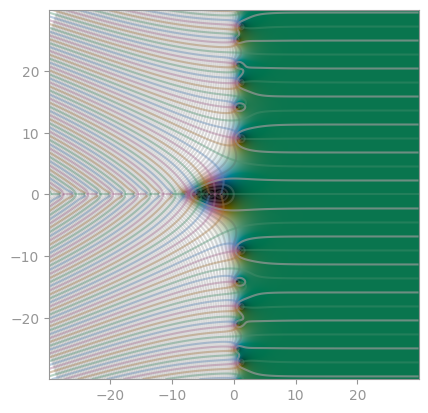
| [Gudermannian function](https://en.wikipedia.org/wiki/Gudermannian_function) |                     Exponential integral E1                      |                     Exponential integral Ei                      |

|      |  |       |

| :------------------------------------------------------------------: | :-------------------------------------------------------------------: | :----------------------------------------------------------------------------: |

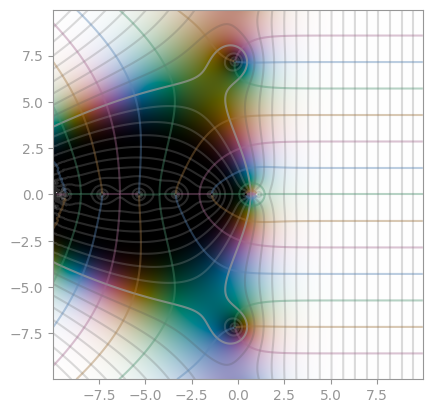
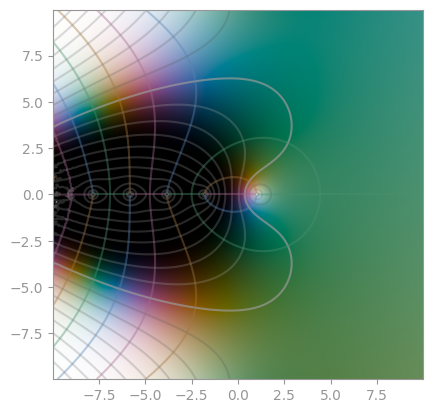
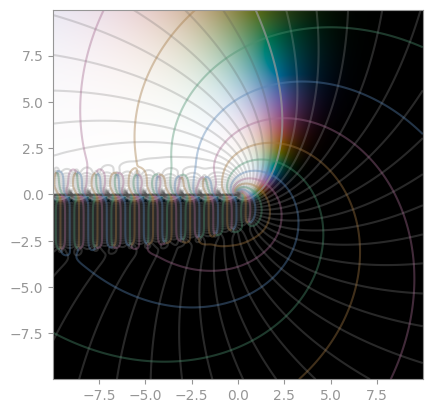
| [`mpmath.zeta`](https://en.wikipedia.org/wiki/Riemann_zeta_function) |                          Bernoulli function                           | [Dirichlet eta function](https://en.wikipedia.org/wiki/Dirichlet_eta_function) |

|                 |  |  |

| :-----------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------: | :-----------------------------------------------------------------------------: |

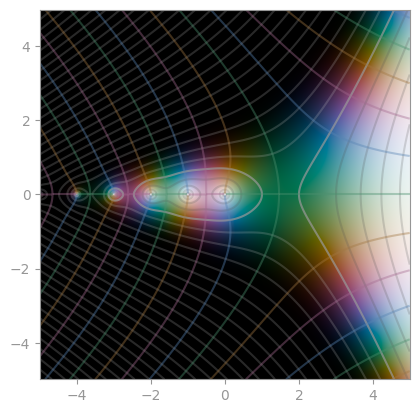
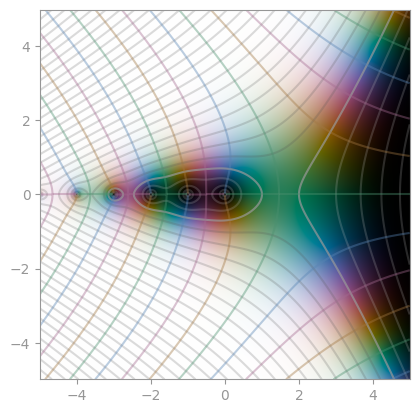
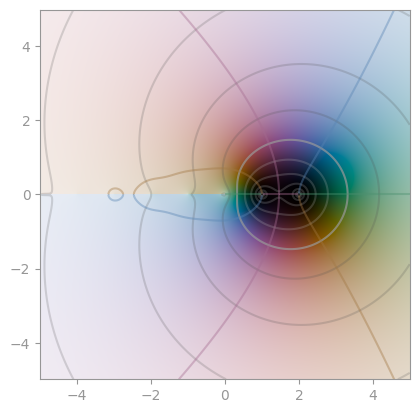
| [Hurwitz zeta function](https://en.wikipedia.org/wiki/Hurwitz_zeta_function) with `a = 1/3` |                     Hurwitz zeta function with `a = 24/25`                     |                     Hurwitz zeta function with `s = 3 + 4i`                     |

|      |  |                             |

| :-------------------------------------------------------------------: | :--------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------------: |

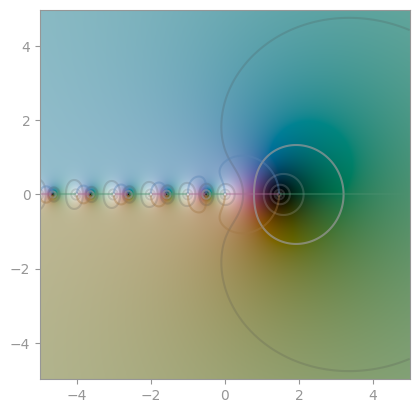
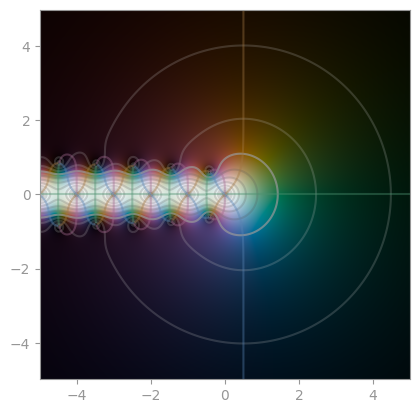
| [`scipy.special.gamma`](https://en.wikipedia.org/wiki/Gamma_function) | [reciprocal Gamma](https://en.wikipedia.org/wiki/Reciprocal_gamma_function)  | [`scipy.special.loggamma`](https://en.wikipedia.org/wiki/Gamma_function#The_log-gamma_function) |

|        |  |  |

| :-----------------------------------------------------------------------: | :--------------------------------------------------------------------: | :--------------------------------------------------------------------: |

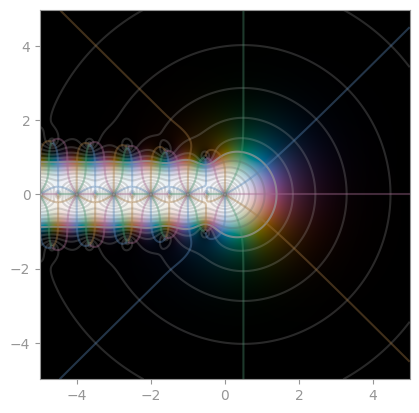
| [`scipy.special.digamma`](https://en.wikipedia.org/wiki/Digamma_function) |    [Polygamma 1](https://en.wikipedia.org/wiki/Polygamma_function)     |    [Polygamma 2](https://en.wikipedia.org/wiki/Polygamma_function)     |

|                      |  |  |

| :--------------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------: | :--------------------------------------------------------------------: |

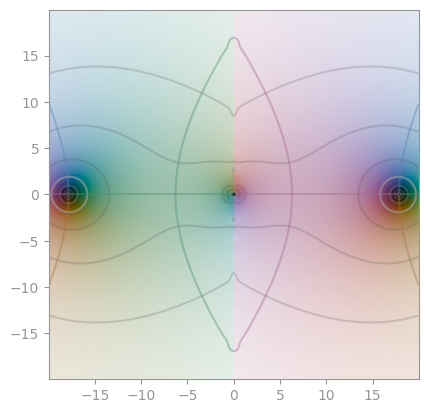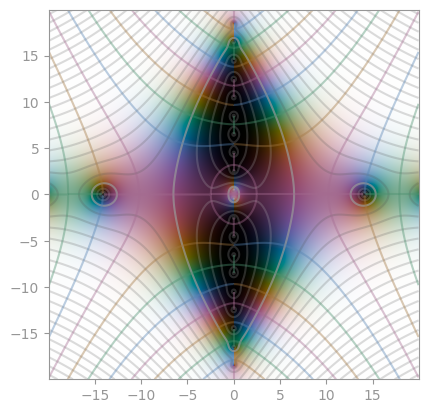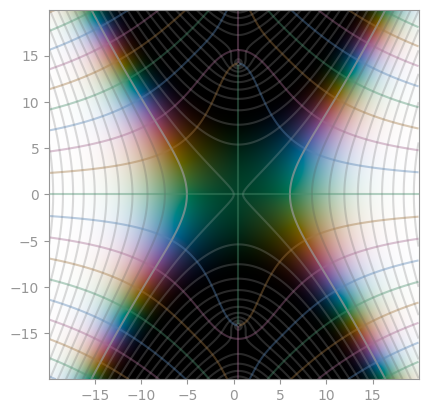| [Riemann-Siegel theta function](https://en.wikipedia.org/wiki/Riemann%E2%80%93Siegel_theta_function) |            [Z-function](https://en.wikipedia.org/wiki/Z_function)            |    [Riemann-Xi](https://en.wikipedia.org/wiki/Riemann_Xi_function)     |

|                       |  |  |

| :-------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------: | :----------------------------------------------------------------------: |

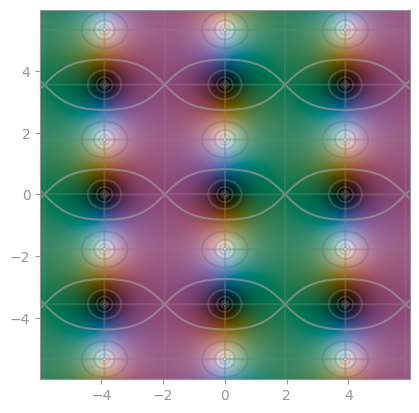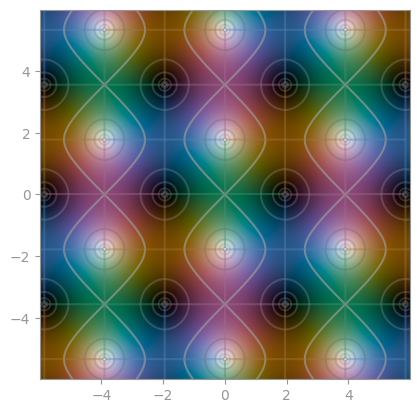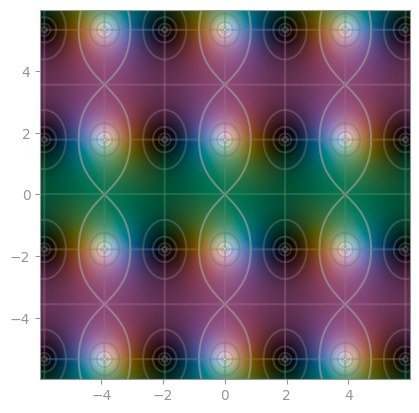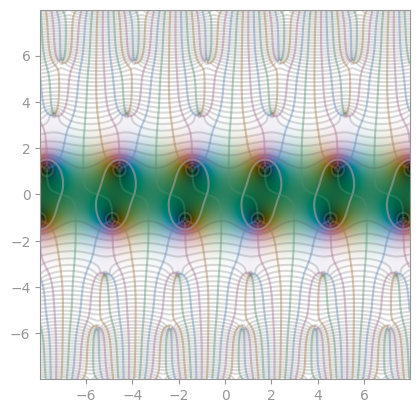
| [Jacobi elliptic function](https://en.wikipedia.org/wiki/Jacobi_elliptic_functions) `sn(0.6)` |                                `cn(0.6)`                                 |                                `dn(0.6)`                                 |

|                               |  |  |

| :----------------------------------------------------------------------------------------------: | :-----------------------------------------------------------------: | :-----------------------------------------------------------------: |

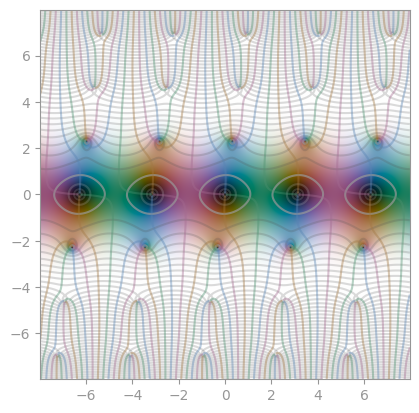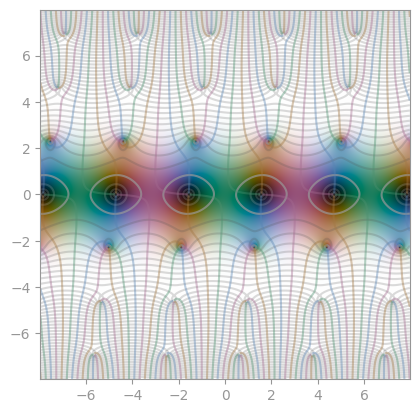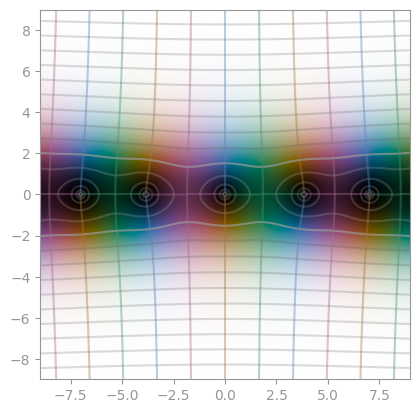
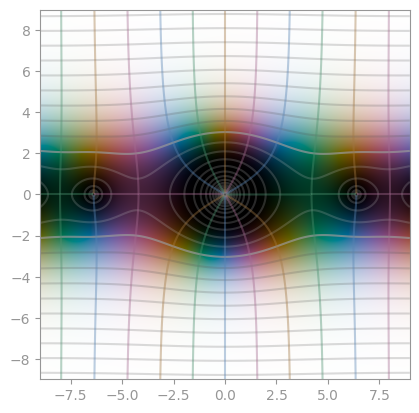
| [Jacobi theta](https://en.wikipedia.org/wiki/Theta_function) 1 with `q=0.1 * exp(0.1j * np.pi))` |                  Jacobi theta 2 with the same `q`                   |                  Jacobi theta 3 with the same `q`                   |

|                  |  |  |

| :-----------------------------------------------------------------------------------: | :-------------------------------------------------------------------: | :-------------------------------------------------------------------: |

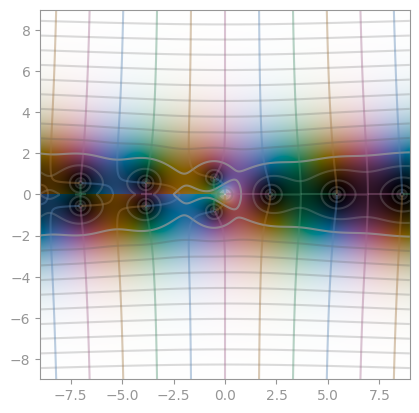
| [Bessel function](https://en.wikipedia.org/wiki/Bessel_function), first kind, order 1 |                 Bessel function, first kind, order 2                  |                 Bessel function, first kind, order 3                  |

|  |  |  |

| :-------------------------------------------------------------------: | :-------------------------------------------------------------------: | :-------------------------------------------------------------------: |

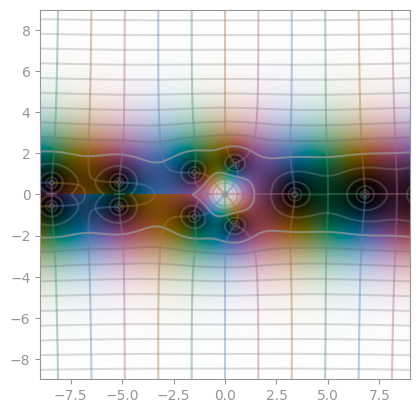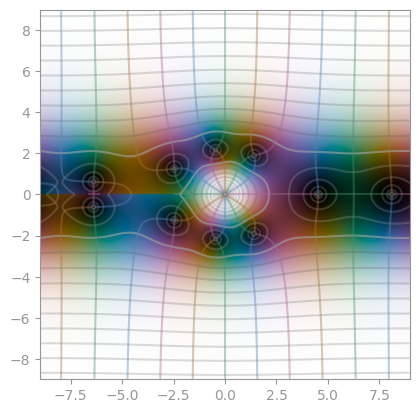|                 Bessel function, second kind, order 1                 |                 Bessel function, second kind, order 2                 |                 Bessel function, second kind, order 3                 |

|  |  |  |

| :------------------------------------------------------------------: | :------------------------------------------------------------------: | :-----------------------------------------------------------------: |

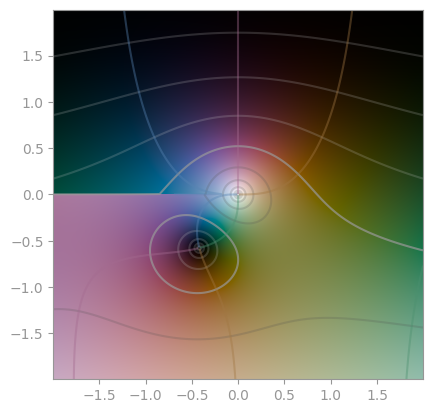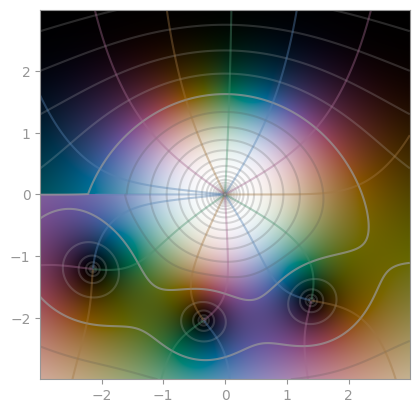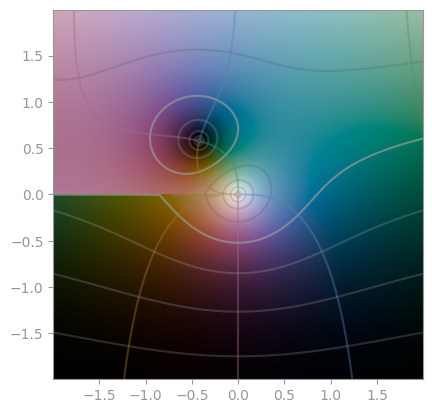|                Hankel function of first kind (n=1.0)                 |                Hankel function of first kind (n=3.1)                 |               Hankel function of second kind (n=1.0)                |

|  |  |  |

| :-------------------------------------------------------------------: | :-------------------------------------------------------------------: | :------------------------------------------------------------------: |

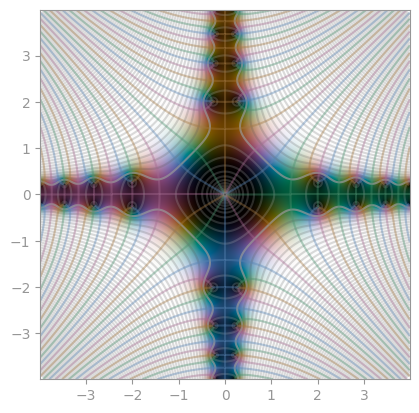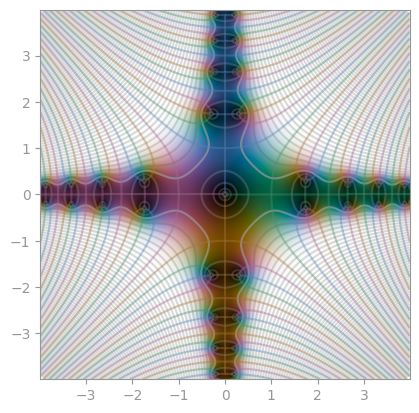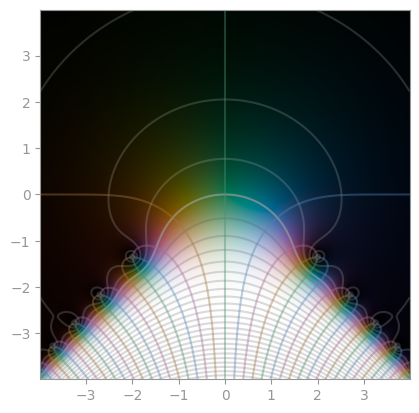|      [Fresnel S](https://en.wikipedia.org/wiki/Fresnel_integral)      |      [Fresnel C](https://en.wikipedia.org/wiki/Fresnel_integral)      | [Faddeeva function](https://en.wikipedia.org/wiki/Faddeeva_function) |

|  |  |     |

| :-----------------------------------------------------------------: | :-----------------------------------------------------------------: | :---------------------------------------------------------------------: |

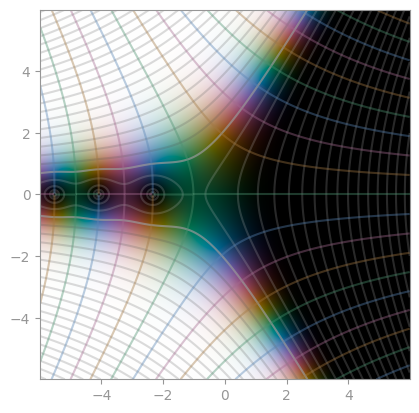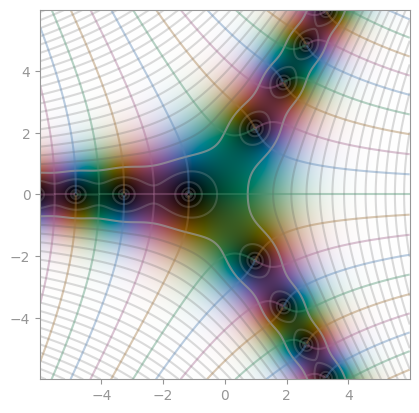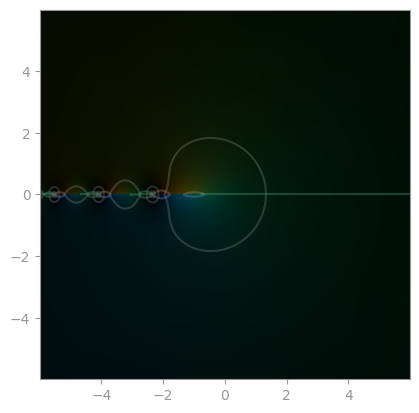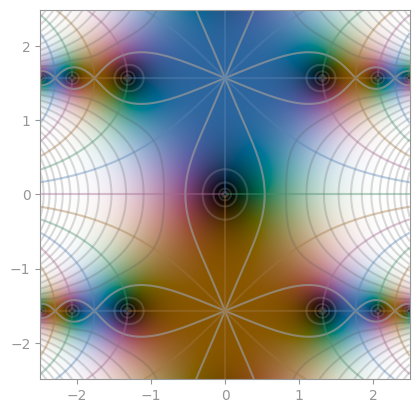
|   [Airy function Ai](https://en.wikipedia.org/wiki/Airy_function)   |          [Bi](https://en.wikipedia.org/wiki/Airy_function)          | [Exponentially scaled eAi](https://en.wikipedia.org/wiki/Airy_function) |

|  |  |  |

| :-------------------------------------------------------------------: | :-------------------------------------------------------------------: | :------------------------------------------------------------------: |

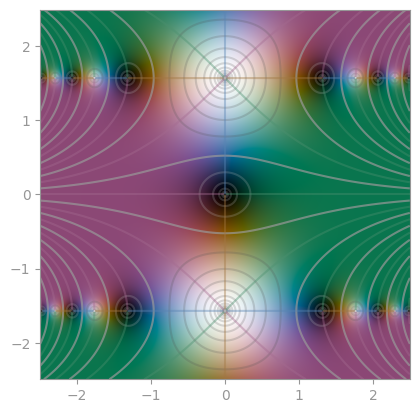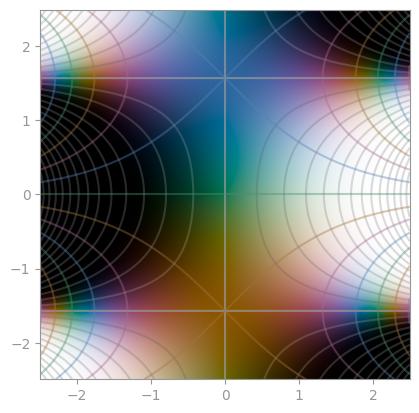
|                       `tanh(pi / 2 * sinh(z))`                        |                       `sinh(pi / 2 * sinh(z))`                        |                       `exp(pi / 2 * sinh(z))`                        |

|  |      |

| :----------------------------------------------------------------: | :--------------------------------------------------------------------------: |

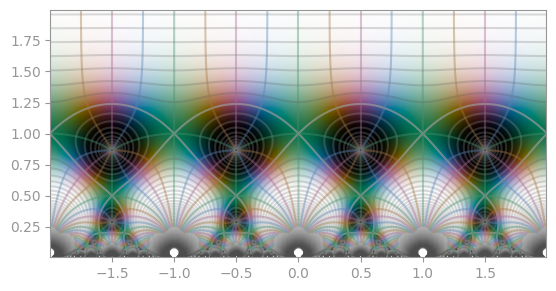
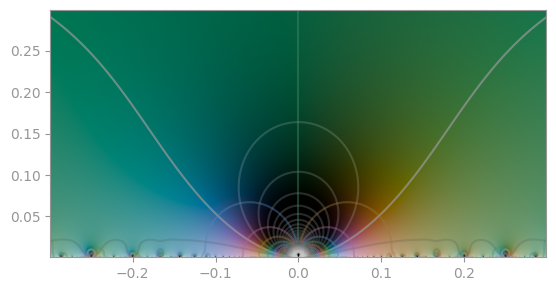
| [Klein's _j_-invariant](https://en.wikipedia.org/wiki/J-invariant) | [Dedekind eta function](https://en.wikipedia.org/wiki/Dedekind_eta_function) |

|   |  |  |

| :--------------------------------------------------------------------: | :------------------------------------------------------------------------------: | :---------------------------------------------------------------------------: |

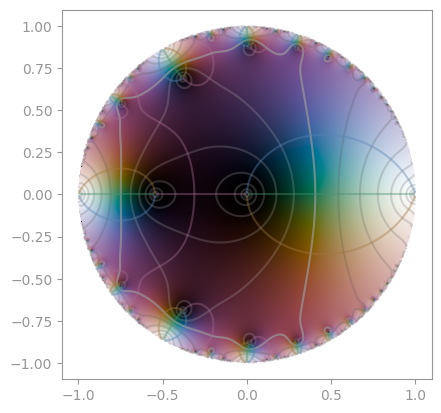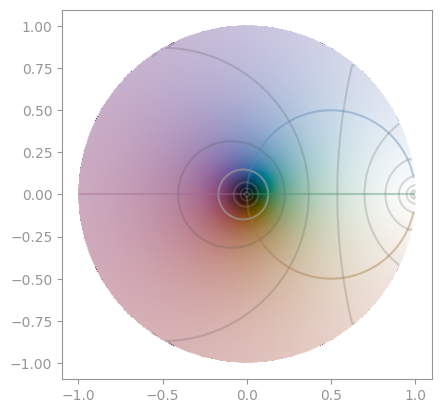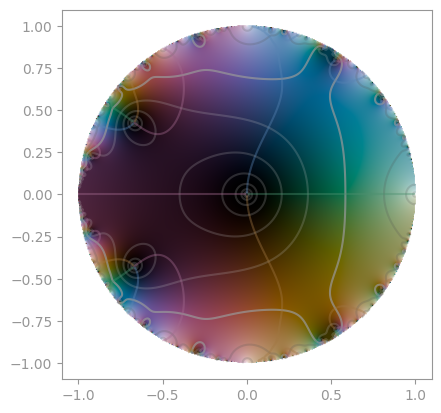| [Lambert series](https://en.wikipedia.org/wiki/Lambert_series) with 1s |                  Lambert series with von-Mangoldt-coefficients                   |                  Lambert series with Liouville-coefficients                   |

### Testing

To run the cplot unit tests, check out this repository and run

```

tox

```

### Similar projects and further reading

- [Tristan Needham, _Visual Complex

  Analysis_, 1997](https://umv.science.upjs.sk/hutnik/NeedhamVCA.pdf)

- [François Labelle, _A Gallery of Complex

  Functions_, 2002](http://wismuth.com/complex/gallery.html)

- [Douglas Arnold and Jonathan Rogness, _Möbius transformations

  revealed_, 2008](https://youtu.be/0z1fIsUNhO4)

- [Konstantin Poelke and Konrad Polthier, _Lifted Domain Coloring_,

  2009](https://doi.org/10.1111/j.1467-8659.2009.01479.x)

- [Elias Wegert and Gunter Semmler, _Phase Plots of Complex Functions:

  a Journey in Illustration_, 2011](https://www.ams.org/notices/201106/rtx110600768p.pdf)

- [Elias Wegert,

  Calendars _Complex Beauties_, 2011-](https://tu-freiberg.de/en/fakult1/ana/institute/institute-of-applied-analysis/organisation/complex-beauties)

- [Elias Wegert, _Visual Complex

  Functions_, 2012](https://www.springer.com/gp/book/9783034801799)

- [empet, _Visualizing complex-valued functions with Matplotlib and Mayavi, Domain coloring method_, 2014](https://nbviewer.org/github/empet/Math/blob/master/DomainColoring.ipynb)

- [John D. Cook, _Visualizing complex

  functions_, 2017](https://www.johndcook.com/blog/2017/11/09/visualizing-complex-functions/)

- [endolith, _complex-colormap_, 2017](https://github.com/endolith/complex_colormap)

- [Anthony Hernandez, _dcolor_, 2017](https://github.com/hernanat/dcolor)

- [Juan Carlos Ponce Campuzano, _DC

  gallery_, 2018](https://www.dynamicmath.xyz/domain-coloring/dcgallery.html)

- [3Blue1Brown, _Winding numbers and domain coloring_, 2018](https://youtu.be/b7FxPsqfkOY)

- [Ricky Reusser, _Domain Coloring with Adaptive

  Contouring_, 2019](https://observablehq.com/@rreusser/adaptive-domain-coloring)

- [Ricky Reusser, _Locally Scaled Domain Coloring, Part 1: Contour

  Plots_, 2020](https://observablehq.com/@rreusser/locally-scaled-domain-coloring-part-1-contour-plots)

- [David Lowry-Duda, _Visualizing modular forms_, 2020](https://arxiv.org/abs/2002.05234)

### License

This software is published under the [GPL-3.0 license](LICENSE). In cases where the

constraints of the GPL prevent you from using this software, feel free contact the

author.