https://github.com/olivierverdier/femshape
Library for computing shape invariants of planar curves using finite element method
https://github.com/olivierverdier/femshape
fenics finite-element-methods math shape
Last synced: 4 months ago
JSON representation
Library for computing shape invariants of planar curves using finite element method
- Host: GitHub
- URL: https://github.com/olivierverdier/femshape
- Owner: olivierverdier
- Created: 2018-11-01T11:16:54.000Z (over 6 years ago)
- Default Branch: master
- Last Pushed: 2019-03-22T10:43:34.000Z (over 6 years ago)
- Last Synced: 2025-01-19T23:37:18.324Z (5 months ago)
- Topics: fenics, finite-element-methods, math, shape
- Language: Jupyter Notebook
- Homepage:
- Size: 2.15 MB
- Stars: 3
- Watchers: 3
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
This is a Python library for computing shape invariants of planar curves using FEM and the FEniCS package. To run the module, [FEniCS](http://fenicsproject.org) must be installed.
It is the supporting code for the paper [Currents and finite elements as tools for shape space](https://arxiv.org/abs/1702.02780) by James Benn, Stephen Marsland, Robert I McLachlan, Klas Modin and Olivier Verdier.
## Getting started ##
The simplest way to calculate the invariants of a curve are as follows.
1. Create a space
```python
space = Space()
```
Check the documentation of the `Space` class to see the available options.
2. Create a curve
This is just an arbitrary array of size P x 2, where P is the number of points.
For instance,
```python
ts = np.arange(0, 2*np.pi, 200)
curve = .7*np.array([np.cos(ts), np.sin(3*ts)]).T
```
3. Compute the associated current
```python
current = Current(space, curve)
```
You have now access to the property `invariants` which contains the result of the current evaluated on the basis of one-forms.
You can inspect the invariants using
```python
plot_invariants(current)
```
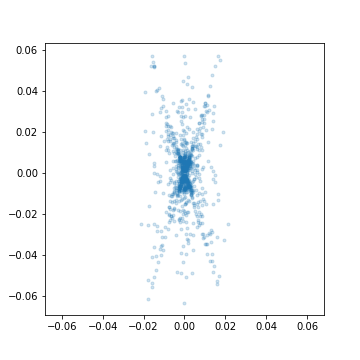
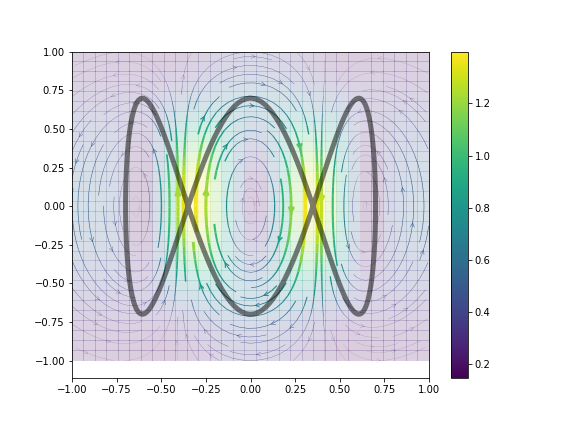
4. Compute the representer
Givne an underlying Hilbert space structure on the one forms, one can compute the associated representer of the current:
```python
representer = Representer(current, scale=.2)
```
You can plot the result using
```python
plot_representer(representer)
```
## Further examples
The notebooks contain further examples:
- [Accuracy of norm computation](https://gist.github.com/olivierverdier/267d1298259f3e0735b49c4e4c88b6a3)
- [Sensitivity with respect to perturbations](https://gist.github.com/olivierverdier/72d2f7b751703f6498f4650be59e4b62)
- [Shape classification with PCA](https://gist.github.com/olivierverdier/9d457d75670d949c0e93321449b60dd0)