Ecosyste.ms: Awesome

An open API service indexing awesome lists of open source software.

Awesome Lists | Featured Topics | Projects

https://github.com/overlordgolddragon/ssqueezepy

Synchrosqueezing, wavelet transforms, and time-frequency analysis in Python
https://github.com/overlordgolddragon/ssqueezepy

cwt morse-wavelet python ridge-extraction signal-processing stft synchrosqueezing time-frequency time-frequency-analysis visualization wavelet-transform

Last synced: 14 days ago
JSON representation

Synchrosqueezing, wavelet transforms, and time-frequency analysis in Python

Awesome Lists containing this project

README 

        



# Synchrosqueezing in Python



[![ssqueezepy CI](https://github.com/OverLordGoldDragon/ssqueezepy/actions/workflows/conda.yml/badge.svg)](https://github.com/OverLordGoldDragon/ssqueezepy/actions/workflows/conda.yml)

[![codecov](https://codecov.io/gh/OverLordGoldDragon/ssqueezepy/branch/master/graph/badge.svg?token=8L7YPN5N19)](https://codecov.io/gh/OverLordGoldDragon/ssqueezepy)

[![PyPI version](https://badge.fury.io/py/ssqueezepy.svg)](https://badge.fury.io/py/ssqueezepy)

[![Codacy Badge](https://app.codacy.com/project/badge/Grade/7cee422639034bcebe0f10ca4b95a506)](https://www.codacy.com/gh/OverLordGoldDragon/ssqueezepy/dashboard?utm_source=github.com&utm_medium=referral&utm_content=OverLordGoldDragon/ssqueezepy&utm_campaign=Badge_Grade)

[![DOI](https://zenodo.org/badge/DOI/10.5281/zenodo.5080508.svg)](https://doi.org/10.5281/zenodo.5080508)

[![License: MIT](https://img.shields.io/badge/License-MIT-green.svg)](https://opensource.org/licenses/MIT)



Synchrosqueezing is a powerful _reassignment method_ that focuses time-frequency representations, and allows extraction of instantaneous amplitudes and frequencies. [Friendly overview.](https://dsp.stackexchange.com/a/71399/50076)



## Features

  - Continuous Wavelet Transform (CWT), forward & inverse, and its Synchrosqueezing

  - Short-Time Fourier Transform (STFT), forward & inverse, and its Synchrosqueezing

  - Wavelet visualizations and testing suite

  - Generalized Morse Wavelets

  - Ridge extraction

  - Fastest wavelet transforms in Python1, beating MATLAB



1: feel free to open Issue showing otherwise



## Installation

`pip install ssqueezepy`. Or, for latest version (most likely stable):



`pip install git+https://github.com/OverLordGoldDragon/ssqueezepy`



## GPU & CPU acceleration



Multi-threaded execution is enabled by default (disable via `os.environ['SSQ_PARALLEL'] = '0'`). GPU requires [CuPy >= 8.0.0](https://docs.cupy.dev/en/stable/install.html)

and [PyTorch >= 1.8.0](https://pytorch.org/get-started/locally/) installed (enable via `os.environ['SSQ_GPU'] = '1'`). `pyfftw` optionally supported for maximum CPU FFT speed.

See [Performance guide](https://github.com/OverLordGoldDragon/ssqueezepy/blob/master/ssqueezepy/README.md#performance-guide).



## Benchmarks



[Code](https://github.com/OverLordGoldDragon/ssqueezepy/blob/master/examples/benchmarks.py). Transforms use padding, `float32` precision (`float64` supported), and output shape

`(300, len(x))`, averaged over 10 runs. `pyfftw` not used, which'd speed 1-thread & parallel further. Benched on author's i7-7700HQ, GTX 1070.



`len(x)`-transform | 1-thread CPU | parallel | gpu | pywavelets | scipy | librosa

:----------------:|:----------------:|:-----------------:|:-----------------:|:-----------------:|:-----------------:|:-----------------:

10k-cwt       | 0.126 | 0.0462 | 0.00393 | 3.58 | 0.523 | -

10k-stft      | 0.108 | 0.0385 | 0.00534 | -    | 0.118 | 0.0909

10k-ssq_cwt   | 0.372 | 0.148  | 0.00941 | -    | -     | -

10k-ssq_stft  | 0.282 | 0.147  | 0.0278  | -    | -     | -

160k-cwt      | 2.99  | 1.25   | 0.0367  | 12.7 | 10.7  | -

160k-stft     | 1.66  | 0.418  | 0.0643  | -    | 1.93  | 1.38

160k-ssq_cwt  | 8.38  | 3.16   | 0.0856  | -    | -     | -

160k-ssq_stft | 4.65  | 2.48   | 0.159   | -    | -     | -



## Questions?



See [here](#asking-questions).



## Examples



### 1. Signal recovery under severe noise



![image](https://user-images.githubusercontent.com/16495490/99879090-b9f12c00-2c23-11eb-8a40-2011ce84df61.png)



### 2. Medical: EEG









### 3. Testing suite: CWT vs STFT, reflect-added parallel A.M. linear chirp






### 4. Ridge extraction: cubic polynom. F.M. + pure tone; noiseless & 1.69dB SNR






[More](https://github.com/OverLordGoldDragon/ssqueezepy/tree/master/examples/ridge_extraction)



### 5. Testing suite: GMW vs Morlet, reflect-added hyperbolic chirp (extreme time-loc.)






### 6. Higher-order GMW CWT, reflect-added parallel linear chirp, 3.06dB SNR






[More examples](https://overlordgolddragon.github.io/test-signals/)



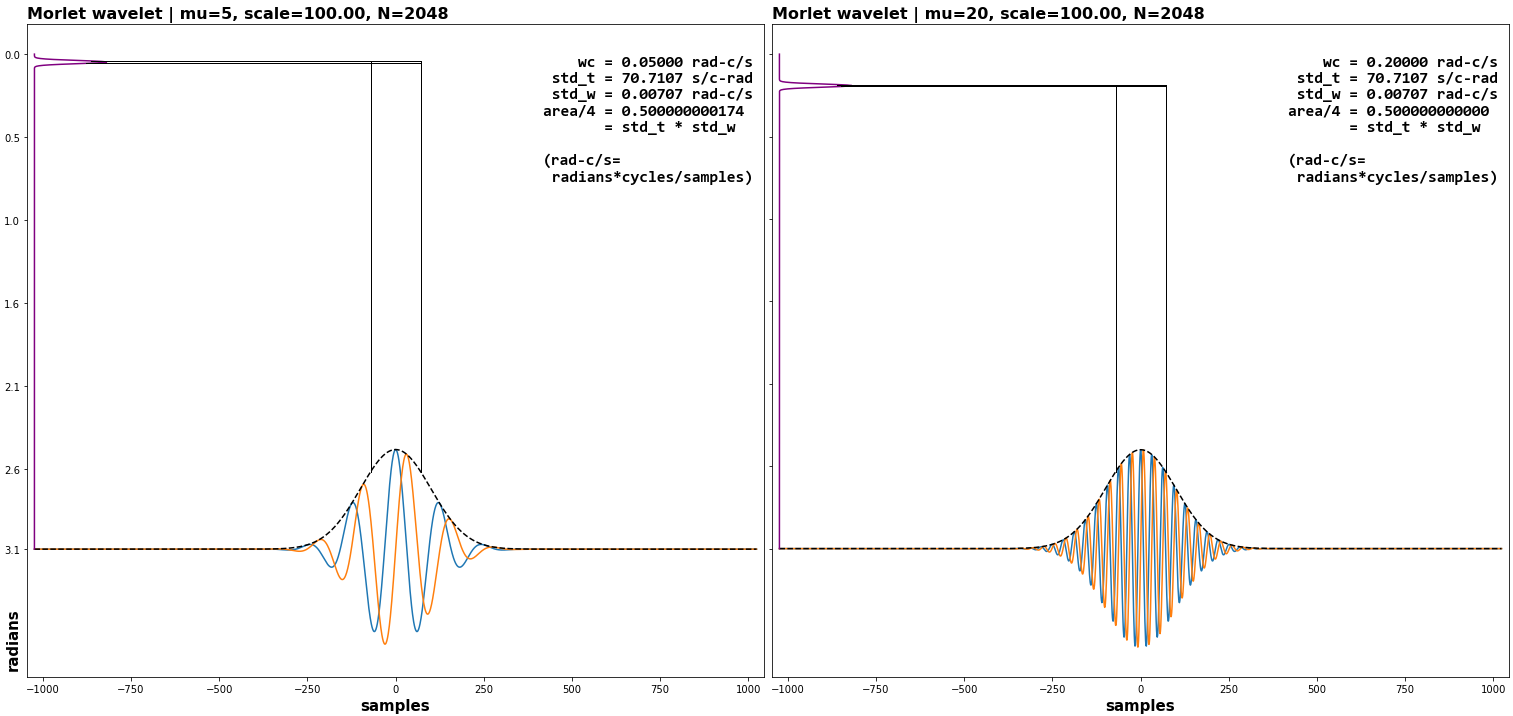
## Introspection



`ssqueezepy` is equipped with a visualization toolkit, useful for exploring wavelet behavior across scales and configurations. (Also see [explanations and code](https://dsp.stackexchange.com/a/72044/50076))





  









## How's it work?



In a nutshell, synchrosqueezing exploits _redundancy_ of a time-frequency representation to sparsely localize oscillations, by imposing a _prior_. That is, we _assume_ `x` is well-captured by AM-FM components, e.g. based on our knowledge of the underlying process. We surpass Heisenberg's limitations, but only for a _subset_ of all possible signals. It's also akin to an _attention_ mechanism.



Convolve with localized, analytic kernels






compute phase transform, then combine oscillations with a shared rate









## Minimal example



```python

import numpy as np

import matplotlib.pyplot as plt

from ssqueezepy import ssq_cwt, ssq_stft

from ssqueezepy.experimental import scale_to_freq



def viz(x, Tx, Wx):

    plt.imshow(np.abs(Wx), aspect='auto', cmap='turbo')

    plt.show()

    plt.imshow(np.abs(Tx), aspect='auto', vmin=0, vmax=.2, cmap='turbo')

    plt.show()



#%%# Define signal ####################################

N = 2048

t = np.linspace(0, 10, N, endpoint=False)

xo = np.cos(2 * np.pi * 2 * (np.exp(t / 2.2) - 1))

xo += xo[::-1]  # add self reflected

x = xo + np.sqrt(2) * np.random.randn(N)  # add noise



plt.plot(xo); plt.show()

plt.plot(x);  plt.show()



#%%# CWT + SSQ CWT ####################################

Twxo, Wxo, *_ = ssq_cwt(xo)

viz(xo, Twxo, Wxo)



Twx, Wx, *_ = ssq_cwt(x)

viz(x, Twx, Wx)



#%%# STFT + SSQ STFT ##################################

Tsxo, Sxo, *_ = ssq_stft(xo)

viz(xo, np.flipud(Tsxo), np.flipud(Sxo))



Tsx, Sx, *_ = ssq_stft(x)

viz(x, np.flipud(Tsx), np.flipud(Sx))



#%%# With units #######################################

from ssqueezepy import Wavelet, cwt, stft, imshow

fs = 400

t = np.linspace(0, N/fs, N)

wavelet = Wavelet()

Wx, scales = cwt(x, wavelet)

Sx = stft(x)[::-1]



freqs_cwt = scale_to_freq(scales, wavelet, len(x), fs=fs)

freqs_stft = np.linspace(1, 0, len(Sx)) * fs/2



ikw = dict(abs=1, xticks=t, xlabel="Time [sec]", ylabel="Frequency [Hz]")

imshow(Wx, **ikw, yticks=freqs_cwt)

imshow(Sx, **ikw, yticks=freqs_stft)

```



Also see ridge extraction [README](https://github.com/OverLordGoldDragon/ssqueezepy/tree/master/examples/ridge_extraction).



## Interesting use cases (with code)



 1. [Identify abrupt changes in audio](https://dsp.stackexchange.com/a/87512/50076) - `ssq_cwt` and `ssq_stft` used together to solve an ML problem without ML

 

Feel free to share yours [here](https://github.com/OverLordGoldDragon/ssqueezepy/issues/9).



## Learning resources



 1. [Continuous Wavelet Transform, & vs STFT](https://ccrma.stanford.edu/~unjung/mylec/WTpart1.html)

 2. [Synchrosqueezing's phase transform, intuitively](https://dsp.stackexchange.com/a/72238/50076)

 3. [Wavelet time & frequency resolution visuals](https://dsp.stackexchange.com/a/72044/50076)

 4. [Why oscillations in SSQ of mixed sines? Separability visuals](https://dsp.stackexchange.com/a/72239/50076)

 5. [Zero-padding's effect on spectrum](https://dsp.stackexchange.com/a/70498/50076)



**DSP fundamentals**: I recommend starting with 3b1b's [Fourier Transform](https://youtu.be/spUNpyF58BY), then proceeding with [DSP Guide](https://www.dspguide.com/CH7.PDF) chapters 7-11.

The Discrete Fourier Transform lays the foundation of signal processing with real data. Deeper on DFT coefficients [here](https://dsp.stackexchange.com/a/70395/50076), also [3b1b](https://youtu.be/g8RkArhtCc4).



## Contributors (noteworthy)



 - [David Bondesson](https://github.com/DavidBondesson): ridge extraction (`ridge_extraction.py`; `examples/`: `extracting_ridges.py`, `ridge_extraction/README.md`)



## Asking questions



Open an Issue, and follow the [Issues Template](https://github.com/OverLordGoldDragon/ssqueezepy/issues/new/choose). Mainly code-related questions go to [Stack Overflow](https://stackoverflow.com/) (SO). Applications, theory questions, etc go elsewhere, e.g. [DSP.SE](https://dsp.stackexchange.com/). I may or may not respond, but others may (or may not) help. I don't follow SO.



**Do not** send e-mail, LinkedIn messages, etc - they will be ignored.



## How to cite



Short form:



> John Muradeli, ssqueezepy, 2020. GitHub repository, https://github.com/OverLordGoldDragon/ssqueezepy/. DOI: 10.5281/zenodo.5080508



BibTeX:



```bibtex

@article{OverLordGoldDragon2020ssqueezepy,

  title={ssqueezepy},

  author={John Muradeli},

  journal={GitHub. Note: https://github.com/OverLordGoldDragon/ssqueezepy/},

  year={2020},

  doi={10.5281/zenodo.5080508},

}

```



## References



`ssqueezepy` was originally ported from MATLAB's [Synchrosqueezing Toolbox](https://github.com/ebrevdo/synchrosqueezing), authored by E. Brevdo and G. Thakur [1]. Synchrosqueezed Wavelet Transform was introduced by I. Daubechies and S. Maes [2], which was followed-up in [3], and adapted to STFT in [4]. Many implementation details draw from [5]. Ridge extraction based on [6].



  1. G. Thakur, E. Brevdo, N.-S. Fučkar, and H.-T. Wu. ["The Synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications"](https://arxiv.org/abs/1105.0010), Signal Processing 93:1079-1094, 2013.

  2. I. Daubechies, S. Maes. ["A Nonlinear squeezing of the Continuous Wavelet Transform Based on Auditory Nerve Models"](https://services.math.duke.edu/%7Eingrid/publications/DM96.pdf).

  3. I. Daubechies, J. Lu, H.T. Wu. ["Synchrosqueezed Wavelet Transforms: a Tool for Empirical Mode Decomposition"](https://arxiv.org/pdf/0912.2437.pdf), Applied and Computational Harmonic Analysis 30(2):243-261, 2011.

  4. G. Thakur, H.T. Wu. ["Synchrosqueezing-based Recovery of Instantaneous Frequency from Nonuniform Samples"](https://arxiv.org/abs/1006.2533), SIAM Journal on Mathematical Analysis, 43(5):2078-2095, 2011.

  5. Mallat, S. ["Wavelet Tour of Signal Processing 3rd ed"](https://www.di.ens.fr/~mallat/papiers/WaveletTourChap1-2-3.pdf).

  6. D. Iatsenko, P. V. E. McClintock, A. Stefanovska. ["On the extraction of instantaneous frequencies from ridges in time-frequency representations of signals"](https://arxiv.org/pdf/1310.7276.pdf).



## License



ssqueezepy is MIT licensed, as found in the [LICENSE](https://github.com/OverLordGoldDragon/ssqueezepy/blob/master/LICENSE) file. Some source functions may be under other authorship/licenses; see [NOTICE.txt](https://github.com/OverLordGoldDragon/ssqueezepy/blob/master/NOTICE.txt).