https://github.com/piotrjustyna/netpolynomial
Single and multivariate polynomial representation for .NET.
https://github.com/piotrjustyna/netpolynomial
Last synced: 7 months ago
JSON representation
Single and multivariate polynomial representation for .NET.
- Host: GitHub
- URL: https://github.com/piotrjustyna/netpolynomial
- Owner: PiotrJustyna
- Created: 2015-12-25T07:48:25.000Z (almost 10 years ago)
- Default Branch: master
- Last Pushed: 2015-12-28T21:29:18.000Z (almost 10 years ago)
- Last Synced: 2025-01-11T16:38:57.451Z (9 months ago)
- Language: C#
- Homepage:
- Size: 1000 KB
- Stars: 1
- Watchers: 2
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Welcome
Welcome to NETPolynomial! This library is written to provide single and multivariate polynomial representation for .NET framework users. Additionally, it allows its users to evaluate polynomial values, provided that coefficients and indeterminates are defined.
# What can I find in NETPolynomial?
NETPolynomial offers a mechanism of representing and evaluating polynomials using .NET framework. Supported are polynomials consisting of finite number of terms, indeterminates, coefficients and of degrees of limited range (positive and negative).
# Application
One of the possible applications of this library is to aid in machine learning tasks. For example, linear and polynomial regressions require a polynomial of certain degree and coefficients to fit the data. Modelling polynomials (defining terms and adjusting coefficients) using this library should make your like easier.
# Examples
## Representing different types of functions
### Linear functions
To represent a linear function, you have to define its shape first - it's common to see linear functions consisting of two terms (one of degree 1, and one of degree 0), so this example will also have two terms.
```csharp
String slope = "a";
String intercept = "b";
String argument = "x";
// Declare all indeterminates and coefficients
Polynomial linearPolynomial = new Polynomial(
new String[] { argument }
, new String[] { slope, intercept });
// Add terms
linearPolynomial.AddTerm(slope, new Dictionary() { { argument, 1.0 } });
linearPolynomial.AddTerm(intercept);
```
This way your polynomial will look like this if you call the *ToString()* method:
```csharp
a * x^1.00 + b
```
Now, since we have the shape of the polynomial defined, we can try to model some simple linear functions using it.
#### y = 2x + 3
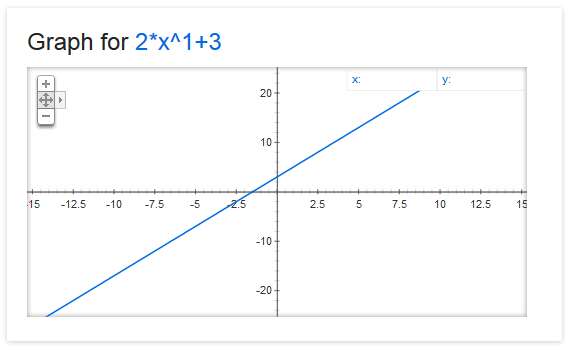
By default, all declared coefficients have value 1.0 and all declared indeterminates have value 0.0, but this can be changed any time:
```csharp
linearPolynomial.SetCoefficientValue(slope, 2.0);
linearPolynomial.SetCoefficientValue(intercept, 3.0);
linearPolynomial.SetIndeterminateValue(argument, 0.0);
```
This way, the polynomial became a function: *y = 2x + 3* (slope is 2.0, *intercept* is 3.0) and its value will be calculated for argument 0.0 (*GetValue()* method).
Full code of this example:
```csharp
String slope = "a";
String intercept = "b";
String argument = "x";
// Declare all indeterminates and coefficients
Polynomial linearPolynomial = new Polynomial(
new String[] { argument }
, new String[] { slope, intercept });
// Add terms
linearPolynomial.AddTerm(slope, new Dictionary() { { argument, 1.0 } });
linearPolynomial.AddTerm(intercept);
// Set coefficients
linearPolynomial.SetCoefficientValue(slope, 2.0);
linearPolynomial.SetCoefficientValue(intercept, 3.0);
// Set the indeterminate
linearPolynomial.SetIndeterminateValue(argument, 0.0);
Console.WriteLine(String.Format("Your polynomial: {0}", linearPolynomial.ToString()));
Console.WriteLine(String.Format("Value for argument 0.0: {0}", linearPolynomial.GetValue()));
```
Output:
```csharp
Your polynomial: a * x^1.00 + b
Value for argument 0.0: 3
```
#### y = -5x + 2
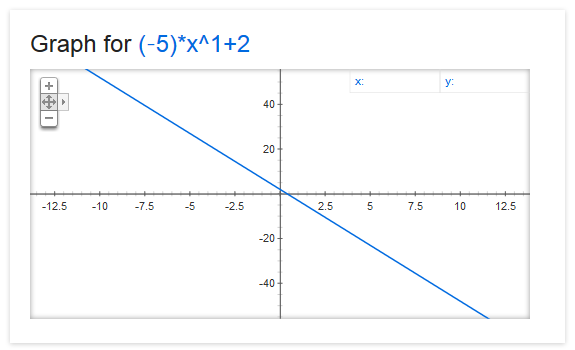
Similarly, our linear polynomial can be easily transformed into this function simply by changing its coefficients:
```csharp
linearPolynomial.SetCoefficientValue(slope, -5.0);
linearPolynomial.SetCoefficientValue(intercept, 2.0);
```
### Planes
#### z = 2x + 3y + 1
Multivariate polynomials can easily represent planes like this one:
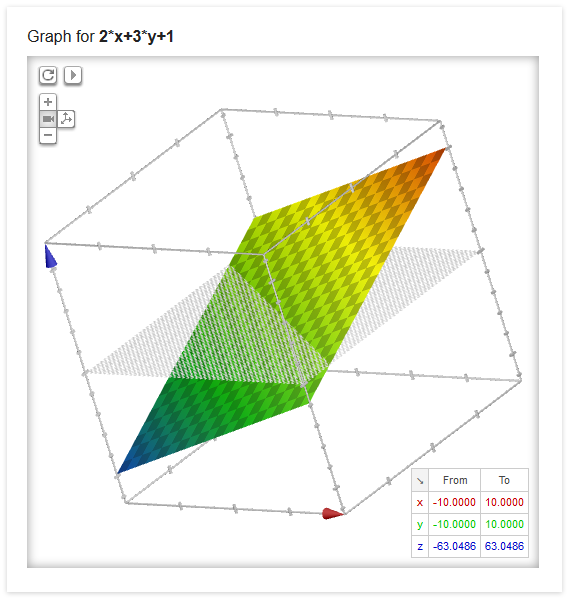
Source code:
```csharp
String a = "a";
String b = "b";
String c = "c";
String x = "x";
String y = "y";
Polynomial linearPolynomial = new Polynomial(
new String[] { x, y }
, new String[] { a, b, c });
linearPolynomial.AddTerm(a, new Dictionary() { { x, 1.0 } });
linearPolynomial.AddTerm(b, new Dictionary() { { y, 1.0 } });
linearPolynomial.AddTerm(c);
linearPolynomial.SetCoefficientValue(a, 2.0);
linearPolynomial.SetCoefficientValue(b, 3.0);
linearPolynomial.SetCoefficientValue(c, 1.0);
linearPolynomial.SetIndeterminateValue(x, 1.0);
linearPolynomial.SetIndeterminateValue(y, 2.0);
```
### Complex Surfaces
#### z = 2x^3 + 15xy + 4y^2 + 5y + 1
Representing more complex functions is just a matter of adding more terms, indeterminates and coefficients. Let's take a look at this graph:
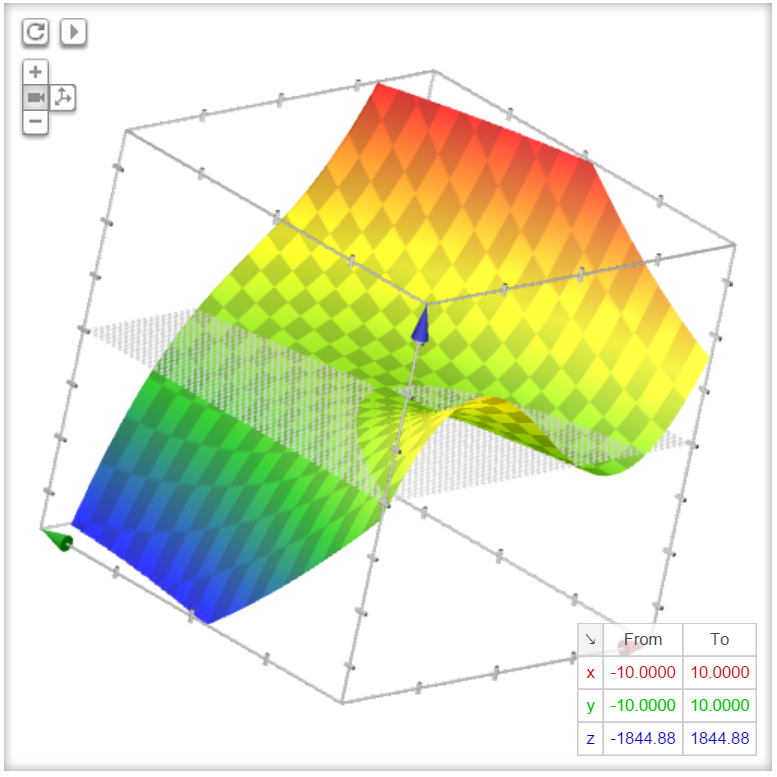
Source code:
```csharp
String a = "a";
String b = "b";
String c = "c";
String d = "d";
String e = "e";
String x = "x";
String y = "y";
Polynomial linearPolynomial = new Polynomial(
new String[] { x, y }
, new String[] { a, b, c, d, e });
linearPolynomial.AddTerm(a, new Dictionary() { { x, 3.0 } });
linearPolynomial.AddTerm(b, new Dictionary()
{
{ x, 1.0 }
, { y, 1.0 }
});
linearPolynomial.AddTerm(c, new Dictionary() { { y, 2.0 } });
linearPolynomial.AddTerm(d, new Dictionary() { { y, 1.0 } });
linearPolynomial.AddTerm(e);
linearPolynomial.SetCoefficientValue(a, 2.0);
linearPolynomial.SetCoefficientValue(b, 15.0);
linearPolynomial.SetCoefficientValue(c, 4.0);
linearPolynomial.SetCoefficientValue(d, 5.0);
linearPolynomial.SetCoefficientValue(e, 1.0);
linearPolynomial.SetIndeterminateValue(x, 1.0);
linearPolynomial.SetIndeterminateValue(y, 2.0);
```
This example shows how you can mix different indeterminates in one term.
## Copying Polynomials
If you face a situation where you have to use multiple structurally similar polynomials (let's say quadratic ones), differing only in the values of their coefficients, you don't have to create each one of them separately. You define your structure once, and then you can deep copy (*Copy()* method) it to create remaining polynomials. After you have a deep copy of your base polynomial, you can then assign desired values to each of the polynomial's coefficients.
## Comparing Polynomials
If you want to compare polynomials, you have two methods at your disposal: *Equals(Object obj)* and *Equals(Polynomial polynomialObject)*. The first one is just overridden .NET *Equals* and lets you compare your polynomials with virtually any object while the second one is more specialised and accepts only instances of the *Polynomial* class.
Comparison is divided into three stages: comparing the structure (quadratic polynomials should not be equal to the cubic ones), comparing the values of coefficients (*2x + 3* is not *2x - 3*) and comparing values of indeterminates (*2x + 3* has different values for *x* = 1 and *x* = 2). If all of these conditions are met, polynomial are equal.