https://github.com/primaryobjects/lsystems

Recursive patterns using Lindenmayer systems.
https://github.com/primaryobjects/lsystems

ai artificial-intelligence canvas canvasjs grammar heuristic heuristics html5-canvas javascript lindenmayer lindenmayer-systems logo react reactjs recursion recursive turtle turtle-graphics

Last synced: 22 days ago
JSON representation

Recursive patterns using Lindenmayer systems.

• Host: GitHub
• URL: https://github.com/primaryobjects/lsystems
• Owner: primaryobjects
• Created: 2019-04-10T22:14:47.000Z (over 5 years ago)
• Default Branch: master
• Last Pushed: 2020-01-22T21:56:09.000Z (almost 5 years ago)
• Last Synced: 2024-10-29T22:50:08.587Z (2 months ago)
• Topics: ai, artificial-intelligence, canvas, canvasjs, grammar, heuristic, heuristics, html5-canvas, javascript, lindenmayer, lindenmayer-systems, logo, react, reactjs, recursion, recursive, turtle, turtle-graphics
• Language: JavaScript
• Size: 354 KB
• Stars: 4
• Watchers: 3
• Forks: 0
• Open Issues: 0
• Metadata Files:
  • Readme: readme.md

Awesome Lists containing this project

README

        
L-Systems

===========

Drawing recursive patterns using a formal grammar heuristic.

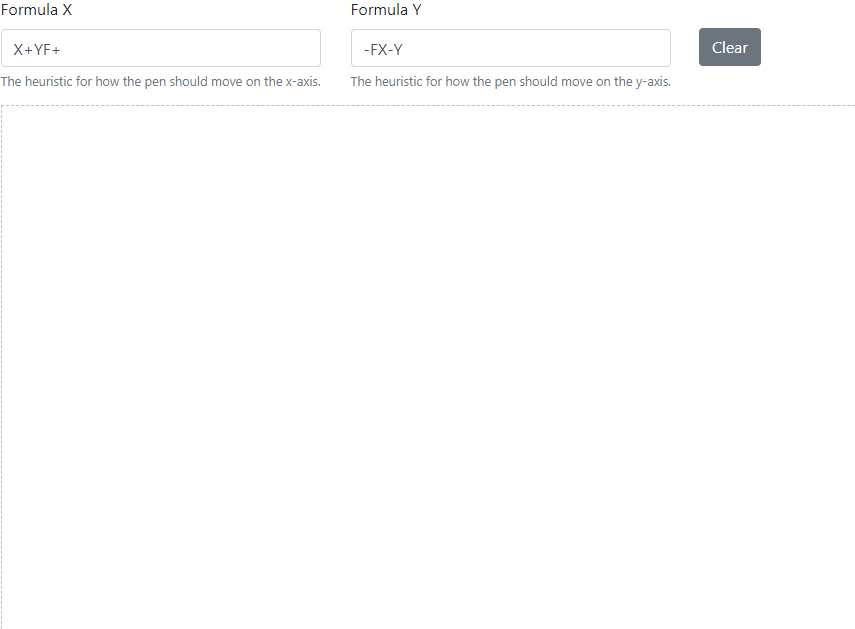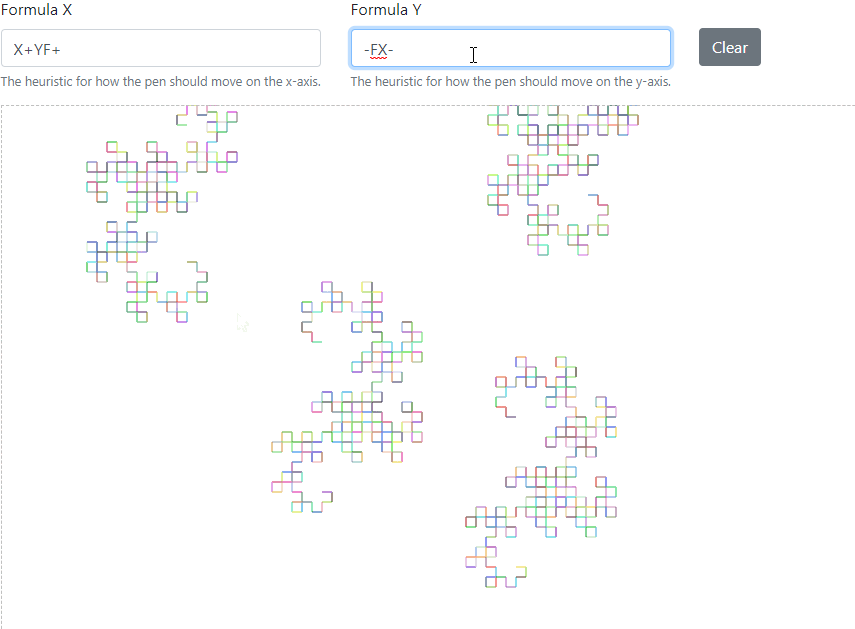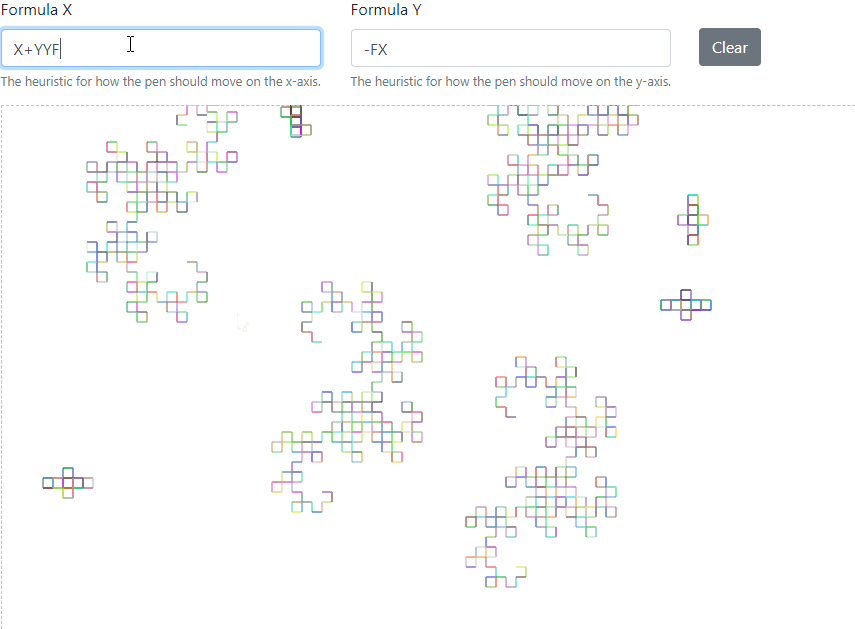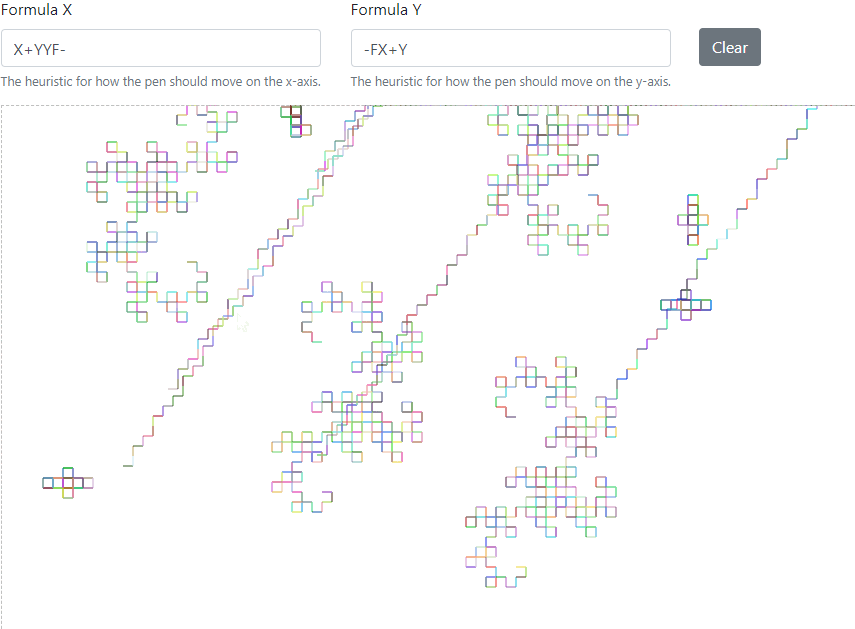
This is a demo of using a [Lindenmayer system](https://en.wikipedia.org/wiki/L-system) to draw patterns using a basic implementation of the programming language [Logo](https://en.wikipedia.org/wiki/Logo_(programming_language)). The pattern is drawn using a heuristic based upon a formula for X and Y movement. The formula is defined using the grammar shown below. The default value is the [Dragon](https://en.wikipedia.org/wiki/L-system#Example_6:_Dragon_curve) pattern!

The project is demonstrated using React, Javascript, and the HTML5 canvas. Run it on [Codepen](https://codepen.io/anon/pen/GLjOOe).

## Screenshot

Try the online [demo](http://primaryobjects.github.io/lsystems/).

![Screenshot](https://raw.githubusercontent.com/primaryobjects/lsystems/master/screenshot.gif)

## Grammar

A lindemayer system consists of a formal grammar, which defines the movement, steps, and direction for the pen to take. This project's grammar is defined below.

```

X = Run the formula for X

Y = Run the formula for Y

F = Move forward by n steps

+ = Turn right by 90 degrees

- = Turn left by 90 degrees

```

From the above set of simple rules, complex patterns can emerge on the canvas. For example, the default formula defines the so-called "Dragon" pattern, which consists of a x-axis movement and a y-axis movement. The definition is listed below.

```

X: X+YF+

Y: -FX-Y

```

For formula X, the grammar dictates that we first execute the X-axis formula for the pen, turn right by 90 degrees, execute the Y-axis formula, move forward (drawing a line), turn right by 90 degrees.

We follow a similar set of steps for formula Y. Since the recursive nature of the grammar would continue running infinitely, we limit the execution of the pattern to a specified number of steps, thus completing the pattern.

## Example Formulas to Try

#### Cross

```

X: X+YF+

Y: -FX

```

#### Diagonal

```

X: X+YYF-

Y: -FX+Y

```

## License

MIT

## Author

Kory Becker

http://www.primaryobjects.com/kory-becker