https://github.com/psygo/misc_algorithms
General Test and Useful Algorithms
https://github.com/psygo/misc_algorithms
Last synced: 6 days ago
JSON representation
General Test and Useful Algorithms
- Host: GitHub
- URL: https://github.com/psygo/misc_algorithms
- Owner: psygo
- Created: 2018-08-12T20:03:13.000Z (over 7 years ago)
- Default Branch: master
- Last Pushed: 2018-08-21T03:24:00.000Z (over 7 years ago)
- Last Synced: 2024-12-29T05:43:03.788Z (12 months ago)
- Language: Jupyter Notebook
- Homepage: http://fanaro.com.br/telecom-nostalgia-and-python-basics/
- Size: 630 KB
- Stars: 0
- Watchers: 2
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# What's inside this Repo?
This is a collection of famous algorithms, which I mainly used to learn more about Python and programming. For more info, visit [fanaro.com.br](http://fanaro.com.br/).
Among them, you will find:
1. Sieve of Eratosthenes
1. Dijkstra's Shortest Path
1. Solution to Problem 51 from Project Euler
1. Erlang's Queueing B Function and Table Generator
## Sieve of Eratosthenes
This is an ancient and simple algorithm created by Eratosthenes of Cyrene, a Greek mathematician. It is one of the most efficient ways of generating primes.
The core of the algorithm is to scratch out all multiples of primes. For example, we first scratch out all of the multiples of 2, then of 3, then of 5, etc. Naturally, the only numbers remaining in the list will be primes.
Two classic improvements have also been added: firstly, you need only to check numbers above and including the square of prime being checked, because the numbers below it will either have been already scratched out by prior primes or are primes; and, secondly, you only need to check multiples of numbers up to the root of the biggest number in the list, since the numbers above it will be checked during the algorithm.
There are other more modern improvements that could be implemented, but, for the sake of simplicity, I'll leave it like this. For more info, you can check [Wikipedia](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes).
## Dijkstra's Shortest Path
Dijkstra's algorithm calculates the shortest path from one node to another within a graph. It is a greedy and very simple algorithm which updates the shortest path every time it checks a new node.
Its implementation usually is usually coupled with special properties (like only checking for roads if you want to do an interstate route search) of the graph/map to lower the complexity of the method, since checking every node can oftentimes be too computationally expensive. In this file, though, only the basic algorithm is implemented. For more info, check [Wikipedia](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm).
## Solution to Problem 51 from Project Euler
Problem 51 is found [here](https://projecteuler.net/archives). It asks you to find the family of 8 numbers containing only primes which have replaceable digits that also yield other primes. For example, 56003 is a prime which can have its 0-digits replaced by others and still yield 6 primes: 56113, 56333, 56433, 56663, 56773 and 56773.
The solution found in this repo (with the files `solve_51.py` and `answer_51.py`) uses pure brute force and can be very inefficient. It first finds all the possible combinations of digits to be replaced and then tries to see if those can make a family of primes by replacing them with other ones. For example, the number of combinations of digits of a 5-digit number would be .
As mentioned before this is very expensive. A first and obvious improvement would be to scratch out the primes which were checked to have families too small to solve the problem. Other improvements use several properties of prime numbers which I didn't know, you can take a look at them [here](https://blog.dreamshire.com/project-euler-51-solution/).
Another detail worth mentioning is that using the *Sieve of Eratosthenes* to solve this problem may not be a good use of your computer, since primes up to 1 million (you always need primes up to  to calculate the families for numbers with 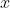 digits) are required. I advise you to use a file with the calculated primes, which can also be found inside the repo.
## Erlang's Queueing B Function and Table Generator
The Erlang B function yields the probability of blockage in a queueing system, given n and the normalized traffic . The formulas can be found [here](https://en.wikipedia.org/wiki/Erlang_(unit)#Erlang_B_formula) and an alternative explanation [here](http://abstractmicro.com/erlang/helppages/mod-b.htm).
Usually, though, you actually have B and n and want to find the traffic E; or you have B and E and want to find n. This used to be done with [tables](http://2.bp.blogspot.com/-iaCH0pVu1iE/Uoh7AZydqSI/AAAAAAAAAFM/ur6uipfGaxc/s1600/Erlang+B.PNG) but nowadays you can implement it in code, and that's what we have here.
To find n, a brute force search was implemented, which finds an n with a smaller or equal probability of blockage given a certain normalized traffic.
To find E, a more refined algorithm can be implemented, which uses gradient descent, since the derivative of  is a continuous function (it could kind of also be done for the other case...).

I've also implemented a less clever search - and an Erlang Table Generator - which only halfs the search interval every time it gets closer to the target. This seems to be a better implementation actually, since it's much less computationally expensive, and it also doesn't have convergence problems due to a learning rate.