https://github.com/ramytanios/fractional-pdes-fem
C++ code for pricing options under Feller-Levy models using the Finite Element Method
https://github.com/ramytanios/fractional-pdes-fem
feynman-kac finite-element-method option-pricing partial-differential-equations
Last synced: about 1 month ago
JSON representation
C++ code for pricing options under Feller-Levy models using the Finite Element Method
- Host: GitHub
- URL: https://github.com/ramytanios/fractional-pdes-fem
- Owner: ramytanios
- Created: 2020-02-17T18:56:45.000Z (about 5 years ago)
- Default Branch: master
- Last Pushed: 2020-09-02T09:27:26.000Z (over 4 years ago)
- Last Synced: 2025-02-07T05:30:26.646Z (3 months ago)
- Topics: feynman-kac, finite-element-method, option-pricing, partial-differential-equations
- Language: C++
- Homepage:
- Size: 2.73 MB
- Stars: 0
- Watchers: 1
- Forks: 2
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Option Pricing under Feller-Lévy models.
* This repository contains the C++ codes for my work as a research assistant at the Seminar for Applied Mathematics at ETH Zürich.
* The topic of my project was: Option Pricing under Feller-Lévy models.
* The codes contain the Finite Element Method implementation for option pricing.
## Overview
The arbitrage-free price of financial products with payoff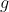 
at time 
, is given by
&space;=&space;\mathbb{E}[e^{-rT}g(X_T)&space;|&space;X_t=x] "V(t,x) = \mathbb{E}[e^{-rT}g(X_T) | X_t=x]")
.
The stock price process follows dt&space;+&space;a(X_{t^-})^{1/\alpha}d&space;L_t^{\alpha},&space;\&space;\&space;\&space;X_0=x, "dX_t = b(X_{t^-})dt + a(X_{t^-})^{1/\alpha}d L_t^{\alpha}, \ \ \ X_0=x,")
, where _{t\ge0} "(L_t^{\alpha})_{t\ge0}")
is an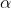 
-stable Lévy process, and hence the stock price is a jump process.
Using the Feynman-Kac theorem, the fractional partial differential equation governing the price of the option is given by
&space;-&space;b(x)\partial_xv(t,x)&space;+&space;a(x)(-\partial_{xx})^{\alpha/2}v(t,x)&space;+&space;rv(t,x)&space;=&space;0,&space;&&space;\text{in}\&space;\mathbb{R}_{>0}\times\mathbb{R}_{\ge0},&space;\\&space;v(0,x)&space;=&space;g(x),&space;&&space;\forall&space;x\in\mathbb{R}_{\ge0}.&space;\end{array}\right. "\label{pricing_eq} \left\{ \begin{array}{@{}ll@{}} v_t(t,x) - b(x)\partial_xv(t,x) + a(x)(-\partial_{xx})^{\alpha/2}v(t,x) + rv(t,x) = 0, & \text{in}\ \mathbb{R}_{>0}\times\mathbb{R}_{\ge0}, \\ v(0,x) = g(x), & \forall x\in\mathbb{R}_{\ge0}. \end{array}\right.")
where 
the risk free interest rate, and 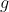the payoff.
Finally, the finite element method is applied to the above equation to solve for the option price process. However, a special numerical treatment is required for the discretization of the fractional laplace operator ^{\alpha/2} "(-\Delta)^{\alpha/2}")
given by ^{-(1-\beta)}=&space;\frac{2\sin(\pi(1-\beta))}{\pi}&space;\int_{-\infty}^{\infty}&space;\text{e}^{2(1-\beta)&space;x}&space;(\mathcal{I}-\text{e}^{2x}\Delta)^{-1}dx "(-\Delta)^{-(1-\beta)}= \frac{2\sin(\pi(1-\beta))}{\pi} \int_{-\infty}^{\infty} \text{e}^{2(1-\beta) x} (\mathcal{I}-\text{e}^{2x}\Delta)^{-1}dx")
, and that is taken care of in this project.