Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/renatogeh/gospn
A free, open-source inference and learning library for Sum-Product Networks (SPN)
https://github.com/renatogeh/gospn
classification dataset deep-learning golang gonum graph hacktoberfest image-reconstruction inference natural-language-processing pgm probability spn statistics
Last synced: 2 months ago
JSON representation
A free, open-source inference and learning library for Sum-Product Networks (SPN)
- Host: GitHub
- URL: https://github.com/renatogeh/gospn
- Owner: RenatoGeh
- License: bsd-3-clause
- Created: 2016-06-22T20:25:16.000Z (over 8 years ago)
- Default Branch: dev
- Last Pushed: 2019-01-16T01:35:10.000Z (almost 6 years ago)
- Last Synced: 2024-10-15T06:09:13.395Z (3 months ago)
- Topics: classification, dataset, deep-learning, golang, gonum, graph, hacktoberfest, image-reconstruction, inference, natural-language-processing, pgm, probability, spn, statistics
- Language: Go
- Homepage:
- Size: 25.7 MB
- Stars: 23
- Watchers: 7
- Forks: 5
- Open Issues: 11
-
Metadata Files:
- Readme: README.md
- Contributing: CONTRIBUTING.md
- License: LICENSE
Awesome Lists containing this project
README
GoSPN
=====
[](https://travis-ci.org/RenatoGeh/gospn)
[](https://goreportcard.com/report/github.com/renatogeh/gospn)
[](https://godoc.org/github.com/RenatoGeh/gospn)
[](https://github.com/RenatoGeh/gospn/blob/dev/LICENSE)

My crude (and slightly terrifying) rendition of Renee French's Go [Gopher](https://blog.golang.org/gopher) writing what's on his mind.
GoSPN: A Sum-Product Network (SPN) Library
------------------------------------------
### Overview
Sum-Product Networks (SPNs) are deep probabilistic graphical models
(PGMs) that compactly represent tractable probability distributions.
Exact inference in SPNs is computed in time linear in the number of
edges, an attractive feature that distinguishes SPNs from other PGMs.
However, learning SPNs is a tough task. There have been many advances in
learning the structure and parameters of SPNs in the past few years. One
interesting feature is the fact that we can make use of SPNs' deep
architecture and perform deep learning on these models. Since the number
of hidden layers not only doesn't negatively impact the tractability of
inference of SPNs but also augments the representability of this model,
it is very much desirable to continue research on deep learning of SPNs.
This project aims to provide a simple framework for Sum-Product
Networks. Our objective is to provide inference tools and implement
various learning algorithms present in literature.
### Roadmap
## All
- [ ] Unit tests
- [ ] Support for continuos variables
## Inference
- [x] Soft inference (marginal probabilities)
- [x] Hard inference (MAP) through max-product algorithm
## Structure learning
- [x] Gens-Domingos learning schema (LearnSPN) [1]
- [x] Dennis-Ventura clustering structural learning algorithm [2]
- [x] Poon-Domingos dense architecture [3]
## Weight learning
- [x] Computation of SPN derivatives
- [x] Soft generative gradient descent
- [x] Hard generative gradient descent
- [x] Soft discriminative gradient descent
- [x] Hard discriminative gradient descent
## Input/Output
- [x] Support for `.npy` files
- [x] Support for `.arff` dataset format (discrete variables only)
- [ ] Support for `.csv` dataset file format
- [x] Support for our own `.data` dataset format
- [x] Serialization of SPNs
### References
- [1] *Learning the Structure of Sum-Product Networks*, R. Gens & P.
Domingos, ICML 2013
- [2] *Learning the Architecture of Sum-Product Networks Using
Clustering on Variables*, A. Dennis & D. Ventura, NIPS 25 (2012)
- [3] *Sum-Product Networks: A New Deep Architecture*, H. Poon & P.
Domingos, UAI 2011
### Looking to contribute?
See the [Contribution
Guidelines](https://github.com/RenatoGeh/gospn/blob/dev/CONTRIBUTING.md).
### Branches
- `dev` contains the development version of GoSPN.
- `stable` contains a stable version of GoSPN.
- `nlp` contains deprecated NLP model.
### Usage
#### As a Go library
GoDocs: https://godoc.org/github.com/RenatoGeh/gospn
Learning algorithms are inside the `github.com/RenatoGeh/gospn/learn`
package, with each algorithm as a subpackage of `learn` (e.g.
`learn/gens`, `learn/dennis`, `learn/poon`).
To parse an ARFF format dataset and perform learning with the
Gens-Domingos structure learning algorithm:
First import the relevant packages (e.g. `learn/gens` for Gens' structural
learning algorithm, `io` for `ParseArff` and `spn` for inference
methods):
```
import (
"github.com/RenatoGeh/gospn/learn/gens"
"github.com/RenatoGeh/gospn/io"
"github.com/RenatoGeh/gospn/spn"
)
```
Extract contents from an ARFF file (for now only discrete variables):
```
name, scope, values, labels := io.ParseArff("filename.arff")
```
Send the relevant information to the learning algorithm:
```
S := gens.Learn(scope, values, -1, 0.0001, 4.0, 4)
```
`S` is the resulting SPN. We can now compute the marginal probabilities
given a `spn.VarSet`:
```
evidence := make(spn.VarSet)
evidence[0] = 1 // Variable 0 = 1
// Summing out variable 1
evidence[2] = 0 // Variable 2 = 0
// Summing out all other variables.
p := S.Value(evidence)
// p is the marginal Pr(evidence), since S is already valid and normalized.
```
The method `S.Value` may repeat calculations if the SPN's graph is not a
tree. To use dynamic programming and avoid recomputations, either use
`spn.Inference` or `spn.Storer`:
```
// This only returns the desired probability (in logspace).
p := spn.Inference(S, evidence)
// A Storer stores values for all nodes.
T := spn.NewStorer()
t := T.NewTicket() // Creates a new DP table.
spn.StoreInference(S, evidence, t, T) // Stores inference values from each node to T(t).
p = T.Single(t, S) // Returns the first value inside node S: T(t, S).
```
Finding the approximate MPE works the same way. Let `evidence` be some
evidence, the MPE is given by:
```
args, mpe := S.ArgMax(evidence) // mpe is the probability and args is the argmax valuation.
```
Similarly to `S.Value`, `S.ArgMax` may recompute values if the graph is
not a tree. Use `StoreMAP` if the graph is a general DAG instead.
```
_, args := spn.StoreMAP(S, evidence, t, T)
mpe := T.Single(t, S)
```
### Dependencies
GoSPN is written in Go. Go is an open source language originally developed
at Google. It's a simple yet powerful and fast language built with
efficiency in mind. Installing Go is easy. Pre-compiled packages are
available for FreeBSD, Linux, Mac OS X and Windows for both 32 and
64-bit processors. For more information see .
#### GoNum
We have deprecated GNU GSL in favor of GoNum ().
GoNum is written in Go, meaning when installing GoSPN, the Go package
manager should automatically install all dependencies (including GoNum).
In case this does not occur and something like this comes up on the
screen:
```
cannot find package "[...]/gonum/stat" in any of
```
Enter the following commands:
```
go get -u gonum.org/v1/gonum/stat
go get -u gonum.org/v1/gonum/mathext
```
We have deprecated functions that made GoSPN independent of GoNum or GNU
GSL, so we recommend installing GoNum.
#### NpyIO
GoSPN supports `.npy` NumPy array dataset. We use
[NpyIO](https://github.com/sbinet/npyio) to read the file and reformat
into GoSPN dataset format. Go's `go get` should automatically install
NpyIO.
#### graph-tool (optional)
Graph-tool is a Python module for graph manipulation and drawing. Since
the SPNs we'll generate with most learning algorithms may have hundreads
of thousands of nodes and hundreds of layers, we need a fast and
efficient graph drawing tool for displaying our graphs. Since graph-tool
uses C++ metaprogramming extensively, its performance is comparable to a
C++ library.
Graph-tool uses the C++ Boost Library and can be compiled with OpenMP, a
library for parallel programming on multiple cores architecture that may
decrease graph compilation time significantly.
Compiling graph-tool can take up to 80 minutes and 3GB of RAM. If you do
not plan on compiling the graphs GoSPN outputs, it is highly recommended
that you do not install graph-tool.
Subdependencies and installation instructions are listed at
.
#### Graphviz (optional)
GoSPN also supports graph drawing with Graphviz. See `io/output.go`.
### Compiling and Running GoSPN
To get the source code through Go's `go get` command, run the following
command:
```
$ go get -u github.com/RenatoGeh/gospn
```
Then ensure all dependencies are pulled:
```
cd gospn && go build
```
### Updating GoSPN
To update GoSPN, run:
```
go get -u github.com/RenatoGeh/gospn
```
### Datasets
For a list of all available datasets in `.data` format, see:
* https://github.com/RenatoGeh/datasets
### Results
Some benchmarking and experiments we did with GoSPN. More can be found
at https://github.com/renatogeh/benchmarks.
#### Image classifications
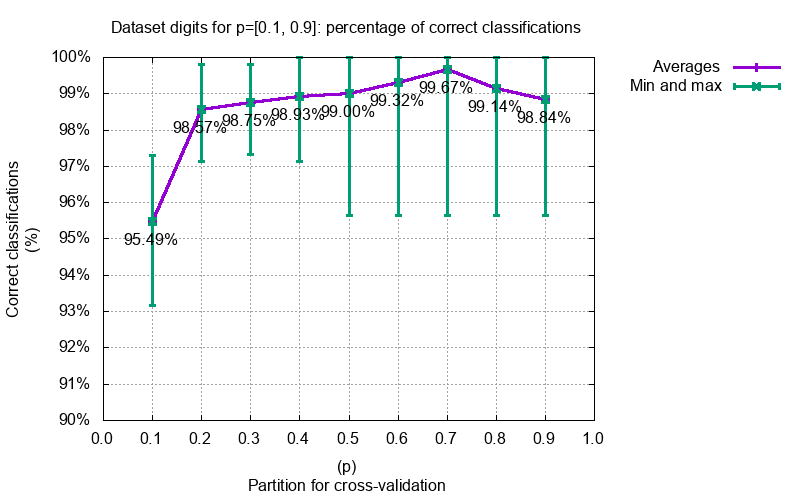
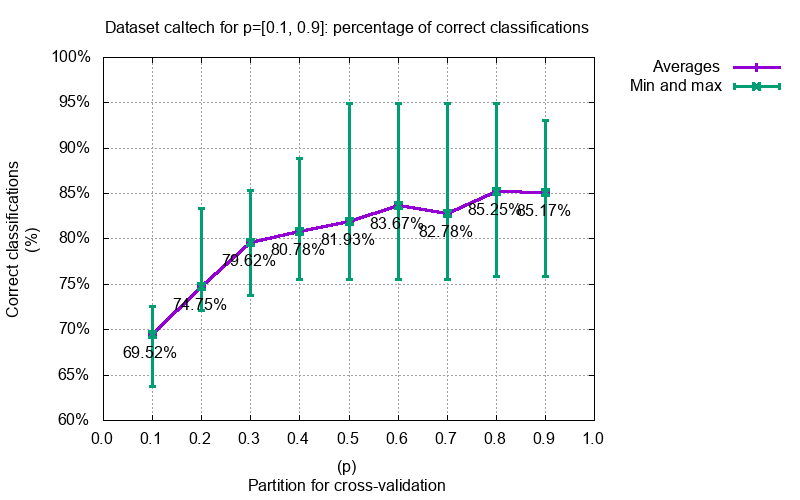
#### Image completions with prior face knowledge


#### Image completions without prior face knowledge


### Literature
The following articles used GoSPN!
- *Credal Sum-Product Networks*, D. Mauá & F. Cozman & D. Conaty & C.
Campos, PMLR 2017
* [pdf](http://proceedings.mlr.press/v62/mau%C3%A117a/mau%C3%A117a.pdf)
- *Approximation Complexity of Maximum A Posteriori Inference in
Sum-Product Networks*, D. Conaty & D. Mauá & C. Campos, UAI 2017
* [pdf](https://arxiv.org/pdf/1703.06045.pdf)
### Acknowledgements
This project is part of my undergraduate research project supervised by
Prof. [Denis Deratani Mauá](https://www.ime.usp.br/~ddm/) at the
Institute of Mathematics and Statistics - University of São Paulo. We
had financial support from CNPq grant #800585/2016-0.
We would like to greatly thank Diarmaid Conaty and Cassio P. de Campos, both
from Queen's University Belfast, for finding and correcting several
bugs.