https://github.com/robbypambudi/prak1_probstat2023_c_5025211042
https://github.com/robbypambudi/prak1_probstat2023_c_5025211042
Last synced: 2 months ago
JSON representation
- Host: GitHub
- URL: https://github.com/robbypambudi/prak1_probstat2023_c_5025211042
- Owner: robbypambudi
- Created: 2023-04-30T15:25:20.000Z (about 2 years ago)
- Default Branch: main
- Last Pushed: 2023-05-01T19:40:48.000Z (about 2 years ago)
- Last Synced: 2025-02-01T19:22:56.349Z (4 months ago)
- Language: R
- Size: 17.6 KB
- Stars: 0
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Prak1_Probstat2023_C_5025211042
- [Prak1\_Probstat2023\_C\_5025211042](#prak1_probstat2023_c_5025211042)
- [Prakikum Modul 1](#prakikum-modul-1)
- [Soal 1](#soal-1)
- [Soal 2](#soal-2)
- [Soal 3](#soal-3)
- [Soal 4](#soal-4)
- [Soal 5](#soal-5)
## Prakikum Modul 1
Nama : Robby Ulung Pambudi
NRP : 5025211042
Kelas: C
### Soal 1
>Probabilitas seorang bayi yang baru lahir berjenis kelamin laki-laki adalah 0,488. Jika kita asumsikan bahwa dalam satu hari di rumah sakit terdapat 10 kalahiran, maka :
a. Bagaimana pendistribusian banyak bayi laki-laki ? Tentukan distribusi dengan parameter yang sesuai
Pendistribusian banyak laki laki dalam 10 kelahiran dapat dihitung dengan menggunakan distribusi binomial, karena setiap kelahiran memiliki dua kemungkinan yaitu laki laki dan perempuan.
Dalam kasus ini, kita dapat menghitung probabilitas dari banyaknya bayi laki laki dalam 10 kelahiran dengan menggunakan distribusi binomial dengan parameter
- n = 10 (banyak kelahiran)
- p = 0.488 (probabilitas bayi laki laki)
```r
# Menghitung probabilitas banyaknya bayi laki laki dalam 10 kelahiran
dbinom(0:10, size = 10, prob = 0.488)
# Membuat grafik distribusi probabilitas
plot(dbinom(0:10, size = 10, prob = 0.488), type = "h", xlab = "Banyaknya bayi laki laki", ylab = "Probabilitas")
```
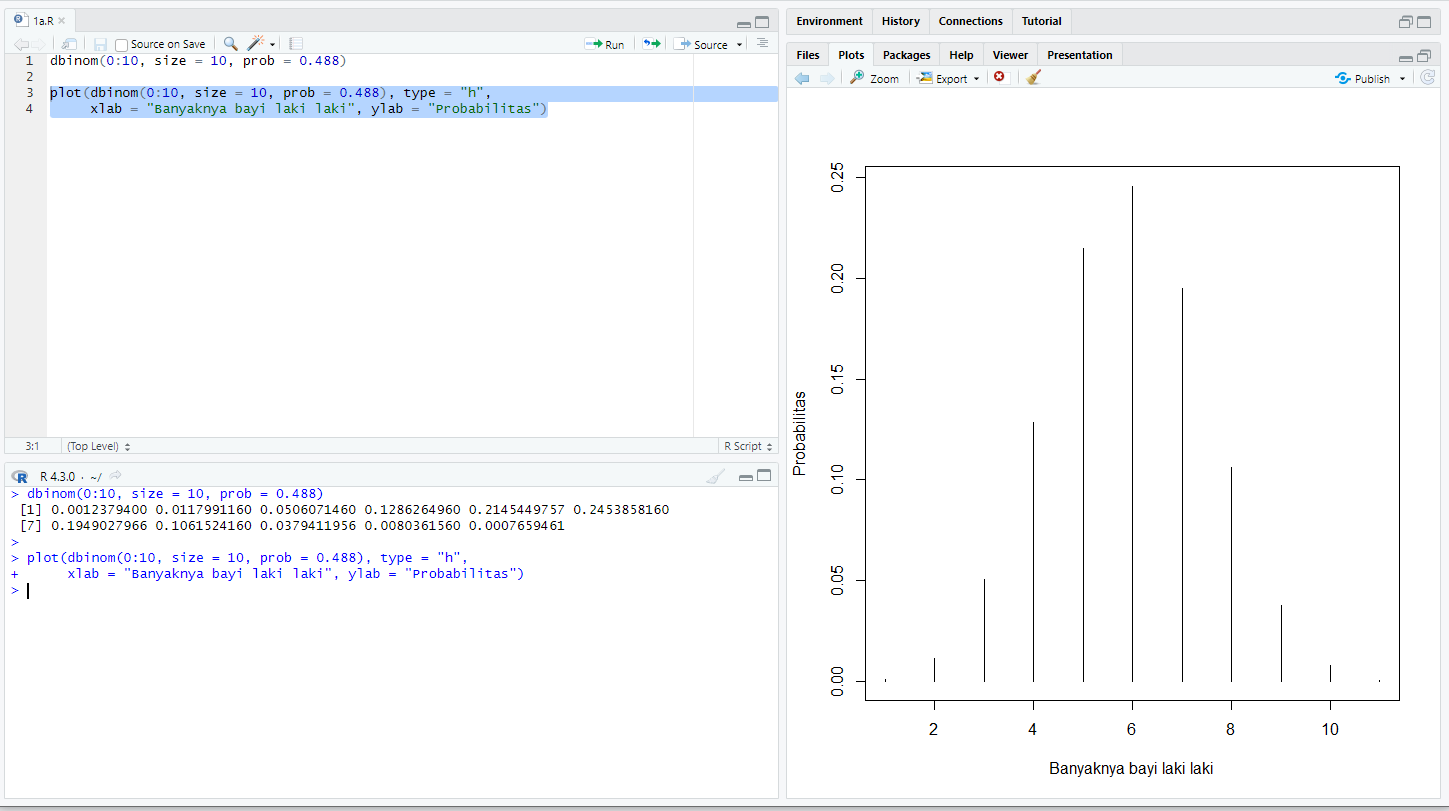
b. Berapa probabilitas bahwa tepat tiga bayi di antaranya berjenis kelamin laki-laki ?
Untuk menghitung probabilitas tepat tiga bayi di antaranya berjenis kelamin laki laki, kita dapat menggunakan fungsi dbinom dengan parameter
- x = 3 (banyaknya bayi laki laki)
- n = 10 (banyak kelahiran)
- p = 0.488 (probabilitas bayi laki laki)
```r
# Menghitung probabilitas tepat tiga bayi di antaranya berjenis kelamin laki laki
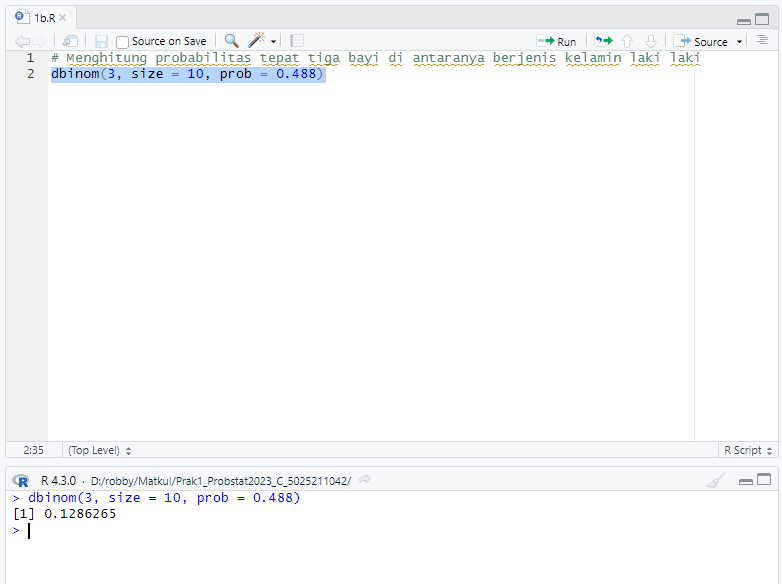
dbinom(3, size = 10, prob = 0.488)
```
```
## [1] 0.1286265
```
Yang artinya probabilitas tepat tiga bayi di antaranya berjenis kelamin laki laki adalah 0.1286265 atau 12.86265%
c. Berapa probabilitas bahwa kurang dari tiga bayi di antaranya berjenis kelamin laki - laki?
Untuk menghitung probabilitas bahwa kurang dari tiga bayi di antaranya berjenis kelamin laki laki, kita dapat menggunakan fungsi `pbinom`, yaitu fungsi yang menghitung probabilitas kumulatif dari distribusi binomial.
Berikut ini adalah sintaks untuk menghitung probabilitas kurang dari tiga bayi di antaranya berjenis kelamin laki laki dengan menggunakan fungsi `pbinom` dengan parameter
- x = 2 (banyaknya bayi laki laki)
- n = 10 (banyak kelahiran)
- p = 0.488 (probabilitas bayi laki laki)
```r
# Menghitung probabilitas kurang dari tiga bayi di antaranya berjenis kelamin laki laki
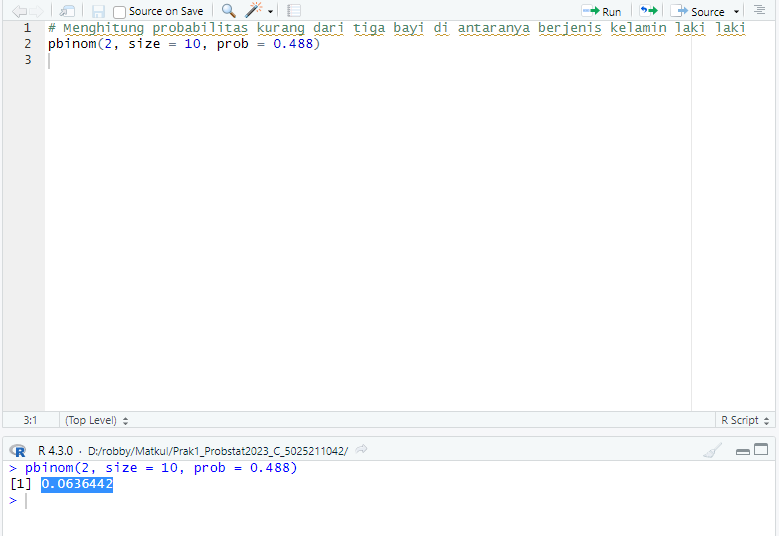
pbinom(2, size = 10, prob = 0.488)
```
```
## [1] 0.0636442
```
Yang artinya probabilitas kurang dari tiga bayi di antaranya berjenis kelamin laki laki adalah 0.0636442 atau 6.36442%
d. Berapa probabilitas bahwa tiga atau lebih bayi di antaranya berjenis kelamin laki-laki?
Untuk menghitung probabilitas bahwa tiga atau lebih bayi di antaranya berjenis kelamin laki laki, kita dapat menggunakan fungsi `pbinom`, yaitu fungsi yang menghitung probabilitas kumulatif dari distribusi binomial.
Kita perlu mengetahui bahwa 0, 1, atau 2 bayi laki laki adalah kebalikan dari tiga atau lebih bayi laki laki. Sehingga, kita dapat menghitung probabilitas tiga atau lebih bayi di antaranya berjenis kelamin laki laki dengan menghitung probabilitas kebalikannya, yaitu 0, 1, atau 2 bayi laki laki.
Berikut ini adalah sintaks untuk menghitung probabilitas tiga atau lebih bayi di antaranya berjenis kelamin laki laki dengan menggunakan fungsi `pbinom` dengan parameter
- x = 2 (banyaknya bayi laki laki)
- n = 10 (banyak kelahiran)
- p = 0.488 (probabilitas bayi laki laki)
```r
# Menghitung probabilitas tiga atau lebih bayi di antaranya berjenis kelamin laki laki
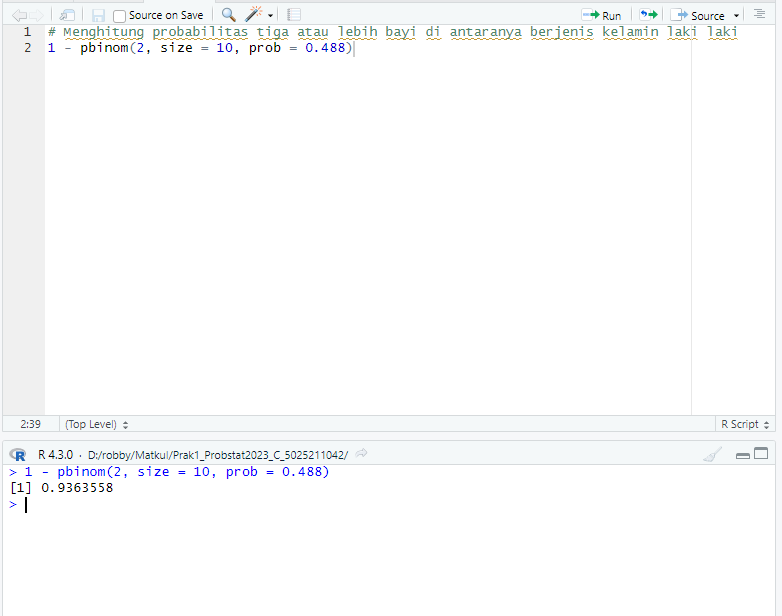
1 - pbinom(2, size = 10, prob = 0.488)
```
```
## [1] 0.9363558
```
Yang artinya probabilitas tiga atau lebih bayi di antaranya berjenis kelamin laki laki adalah 0.9363558 atau 93.63558%
e. Berapa nilai harapan dan simpangan baku dari banyak laki-laki?
Untuk menghitung nilai harapan dan simpangan baku bayi laki-laki, kita dapat menggunakan rumus matematis berikut ini :
- Nilai Harapan: $E(X) = n * p$
- Simpangan Baku: $SD(X) = \sqrt{n * p * (1 - p)}$
Dalam hal ini, nilai n adalah 10 dan nilai p adalah 0.488. Sehingga, kita dapat menghitung nilai harapan dan simpangan baku bayi laki-laki dengan menggunakan sintaks berikut ini :
```r
# Menghitung nilai harapan bayi laki laki
nilai_harapan = 10 * 0.488
simpangan_baku = sqrt(10 * 0.488 * (1 - 0.488))
# Menampilkan nilai harapan dan simpangan baku bayi laki laki
print(paste("Nilai harapan bayi laki laki adalah", nilai_harapan))
print(paste("Simpangan baku bayi laki laki adalah", simpangan_baku))
```
```
Nilai harapan bayi laki laki adalah 4.88
Simpangan baku bayi laki laki adalah 1.58068339650924
```
f. Gambarkan histogram pendistribusian banyak bayi laki-laki
Untuk menggambarkan histogram pendistribusian banyak bayi laki laki, kita dapat menggunakan fungsi `hist` dalam bahasa R. Kita perlu menghasilkan serangkain nilai pada interval diskrit dari 0 hingga 10 yang merupakan jumlah kemungkinan bayi laki laki. Sehingga, kita dapat menggunakan fungsi `seq` untuk menghasilkan serangkain nilai pada interval diskrit dari 0 hingga 10. Kemudian, kita dapat menggunakan fungsi `dbinom` untuk menghitung probabilitas dari setiap nilai pada interval diskrit dari 0 hingga 10.
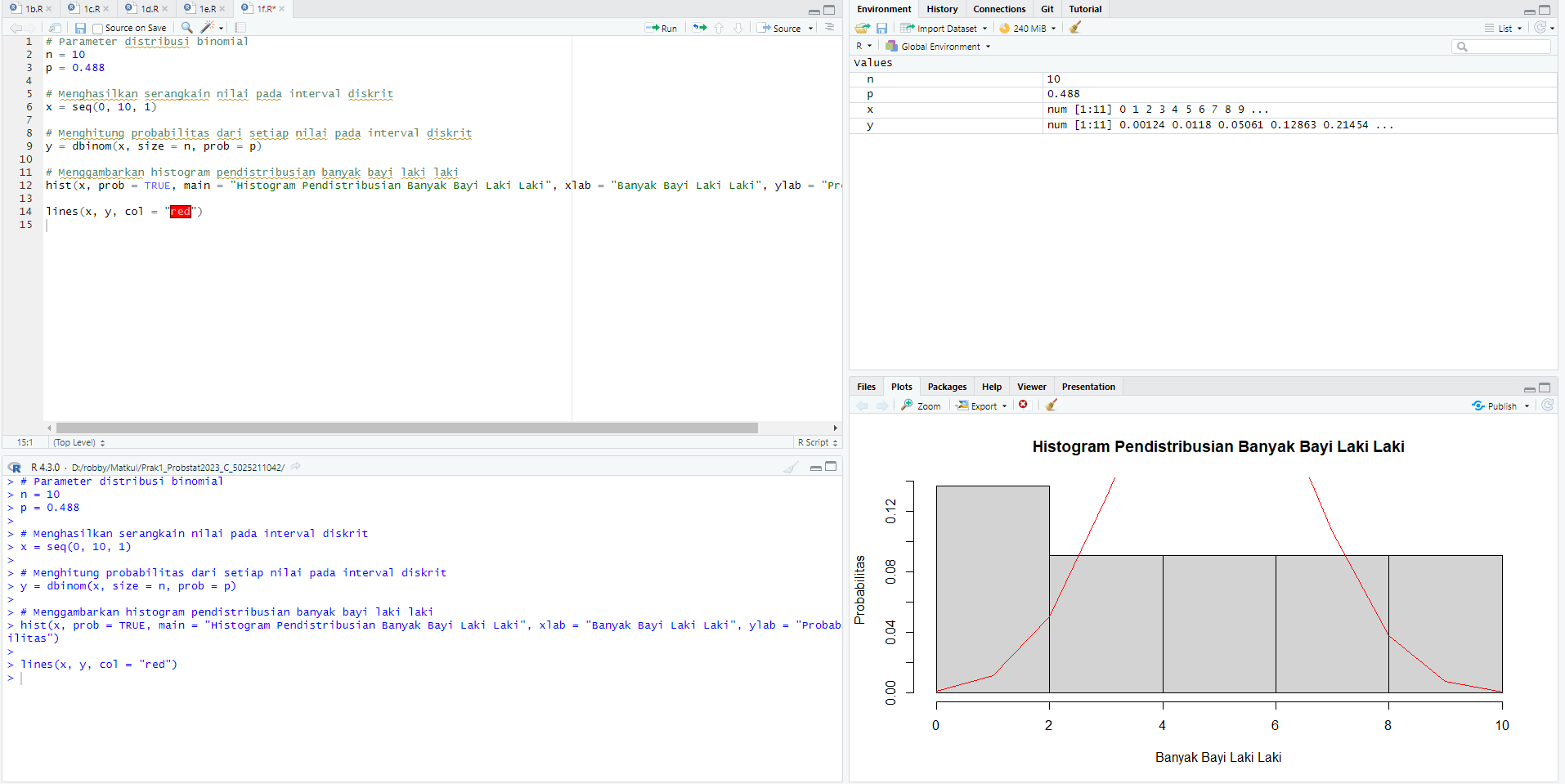
Berikut ini adalah sintaks untuk menggambarkan histogram pendistribusian banyak bayi laki laki dengan menggunakan fungsi `hist`
```r
# Parameter distribusi binomial
n = 10
p = 0.488
# Menghasilkan serangkain nilai pada interval diskrit
x = seq(0, 10, 1)
# Menghitung probabilitas dari setiap nilai pada interval diskrit
y = dbinom(x, size = n, prob = p)
# Menggambarkan histogram pendistribusian banyak bayi laki laki
hist(x, prob = TRUE, main = "Histogram Pendistribusian Banyak Bayi Laki Laki", xlab = "Banyak Bayi Laki Laki", ylab = "Probabilitas")
lines(x, y, col = "red")
```
### Soal 2
> Misalkan banyak kematian karena kanker tulang untuk seluruh pekerja di pabrik ban dalam 20 tahun ke depan adalah 1,8.
a. Bagaimana pendistribusian banyak kematian karena kanker tulang? Tentukan
distribusi dengan parameter yang sesuai.
Untuk menentukan distribusi dengan parameter yang sesuai, kita perlu mengetahui bahwa banyak kematian karena kanker tulang adalah diskrit dan tidak negatif. Sehingga, kita dapat menggunakan distribusi Poisson untuk menentukan distribusi dengan parameter yang sesuai.
Untuk menentukan parameter dari distribusi Poisson, kita perlu mengetahui bahwa nilai harapan dari distribusi Poisson adalah 1.8. Sehingga, kita dapat menggunakan nilai harapan untuk menentukan parameter dari distribusi Poisson.
Dalam hal ini, nilai harapan adalah 1.8. Sehingga, kita dapat menentukan parameter dari distribusi Poisson dengan menggunakan sintaks berikut ini :
```r
# Menentukan parameter dari distribusi Poisson
jumlah_kematian = 1.8
waktu = 20
# Menampilkan parameter dari distribusi Poisson
lamda = jumlah_kematian / waktu
print(paste("Parameter dari distribusi Poisson adalah", lamda))
```
```
## [1] "Parameter dari distribusi Poisson adalah 0.09"
```
b. Ada 4 kematian akibat kanker tulang yang dilaporkan di kalangan pekerja
pabrik ban, apakah itu peristiwa yang tidak biasa? Hitung probabilitas
berdasarkan distribusi yang telah dipilih.
Untuk menghitung probabilitas 4 kematian akibat kanker tulang dalam 20 tahun di pabrik bambu, kita dapat menggunakan fungsi `dpois` untuk menghitung probabilitas dari peristiwa tersebut. Berikut ini adalah sintaks untuk menghitung probabilitas dari peristiwa tersebut :
```r
# Menghitung probabilitas dari peristiwa tersebut
dpois(4, lambda = 0.09)
```
```r
# [1] 2.498459e-06
```
Artinya, probabilitas dari peristiwa tersebut adalah 2.498459e-06. Sehingga, peristiwa tersebut adalah peristiwa yang tidak biasa. Karena probabilitas dari peristiwa tersebut adalah sangat kecil.
c. Berapa peluang paling banyak 4 kematian akibat kanker tulang?
Untuk mencari peluang paling banyak 4 kematian akibat kanker tulang, kita perlu menjumlah probabilitas dari 0 hingga 4. Sehingga, kita dapat menggunakan fungsi `ppois` untuk menghitung probabilitas dari peristiwa tersebut. Berikut ini adalah sintaks untuk menghitung probabilitas dari peristiwa tersebut :
```r
# Menghitung probabilitas dari peristiwa tersebut
ppois(4, lambda = 0.09)
```
```r
# [1] 0.9999998
```
Artinya, peluang paling banyak 4 kematian akibat kanker tulang adalah 0.9999998 atau 99.99998%. Sehingga, peluang paling banyak 4 kematian akibat kanker tulang adalah sangat besar.
d. Berapa peluang lebih dari 4 kematian akibat kanker tulang?
Untuk menghitung peluang lebih dari 4 kematian akibat kanker tulang, kita dapat menggunakan fungsi `ppois` untuk menghitung probabilitas dari peristiwa tersebut. Berikut ini adalah sintaks untuk menghitung probabilitas dari peristiwa tersebut :
```r
# Menghitung probabilitas dari peristiwa tersebut
1 - ppois(4, lambda = 0.09)
```
```r
# [1] 4.565562e-08
```
Artinya, peluang lebih dari 4 kematian akibat kanker tulang adalah 4.565562e-08 atau 0.000004565562%. Sehingga, peluang lebih dari 4 kematian akibat kanker tulang adalah sangat kecil.
e. Berdasarkan distribusi yang telah dipilih, berapakah nilai harapan dan standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban?
Untuk distribusi Poisson dengan parameter lambda, nilai harapan dan standar deviasi dapat dihitung dengan menggunakan rumus berikut ini :
- Nilai harapan = $\lambda$
- Standar deviasi = $\sqrt{\lambda}$
Sehingga, kita dapat menggunakan rumus tersebut untuk menghitung nilai harapan dan standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban. Berikut ini adalah sintaks untuk menghitung nilai harapan dan standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban :
```r
lambda = 0.09
# Menghitung nilai harapan dan standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban
nilai_harapan = lambda
standar_deviasi = sqrt(lambda)
print(paste("Nilai harapan banyak kematian akibat kanker tulang untuk pekerja pabrik ban adalah", nilai_harapan))
print(paste("Standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban adalah", standar_deviasi))
```
```
[1] "Nilai harapan banyak kematian akibat kanker tulang untuk pekerja pabrik ban adalah 0.09"
[1] "Standar deviasi banyak kematian akibat kanker tulang untuk pekerja pabrik ban adalah 0.3"
```
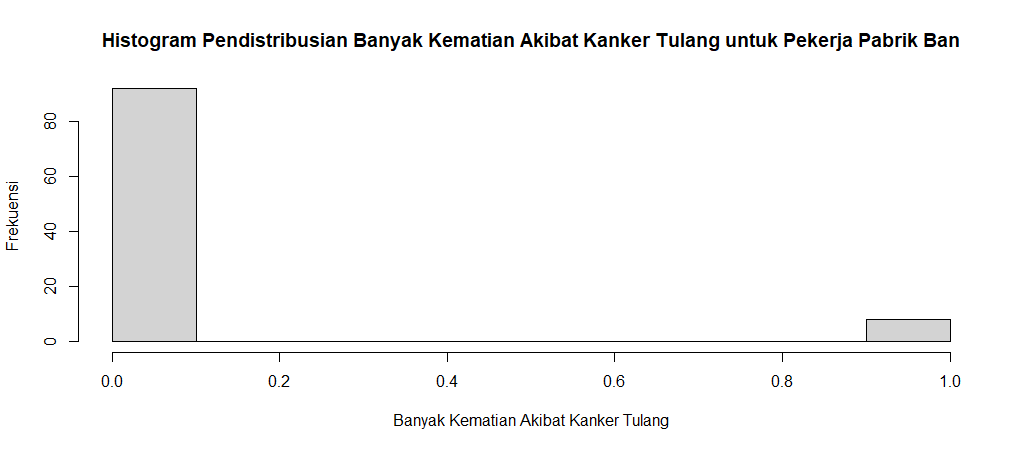
f. Gambarkan histogram pendistribusian banyak banyak kematian akibat kanker
tulang untuk pekerja pabrik ban.
Untuk menggambarkan histogram pendistribusian banyak banyak kematian akibat kanker tulang untuk pekerja pabrik ban, kita dapat menggunakan fungsi `rpois`, rpois merupakan fungsi yang digunakan untuk menghasilkan sampel acak dari distribusi Poisson. Berikut ini adalah sintaks untuk menggambarkan histogram pendistribusian banyak banyak kematian akibat kanker tulang untuk pekerja pabrik ban :
```r
n = 10
lambda = 0.09
# Menghasilkan sampel acak dari distribusi Poisson
sampel = rpois(n, lambda)
# Menggambarkan histogram pendistribusian banyak banyak kematian akibat kanker tulang untuk pekerja pabrik ban
hist(sampel, main = "Histogram Pendistribusian Banyak Kematian Akibat Kanker Tulang untuk Pekerja Pabrik Ban", xlab = "Banyak Kematian Akibat Kanker Tulang", ylab = "Frekuensi")
```
g. Gunakan simulasi untuk memeriksa hasil sebelumnya.
Kita dapat menggunakan simulasi untuk memeriksa hasil sebelumnya. Dalam simulasi ini, kita akan menghasilkan banyak kematian akibat kanker tulang dalam 20 tahun dengan mangambil sample sebanyak 1000 kali. Kemudian menghitung proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang. Berikut ini adalah sintaks untuk melakukan simulasi :
```r
# Parameter distribusi Poisson
lambda = 0.09
# Menghasilkan banyak kematian akibat kanker tulang dalam 20 tahun dengan mangambil sample sebanyak 1000 kali
n_simulasi = 1000
n_deaths = rep(0, n_simulasi)
# Menghitung proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang
for (i in 1:n_simulasi) {
n_deaths[i] = rpois(1, lambda = lambda * 20)
}
# Menghitung proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang
prop = mean(n_deaths >= 4)
print(paste("Proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang adalah", prop))
# Menghitung proporsi kasus di mana terjadi 4 atau kurang kematian akibat kangker tulang
prop = mean(n_deaths <= 4)
print(paste("Proporsi kasus di mana terjadi 4 atau kurang kematian akibat kangker tulang adalah", prop))
```
```
"Proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang adalah 0.121"
"Proporsi kasus di mana terjadi 4 atau kurang kematian akibat kangker tulang adalah 0.963"
```
h. Bandingkan hasil simulasi dengan 2D
Berdasarkan hasil simulasi, proporsi kasus di mana terjadi 4 atau lebih kematian akibat kangker tulang adalah 0.121. Sedangkan, berdasarkan hasil perhitungan menggunakan fungsi `ppois`, proporsi kasus di mana terjadi 4 atau lebuh kematian akibat kangker tulang adalah 0.000004565562%.
Kemudian untuk hasil simulasi proporsi kasus di mana terjadi 4 atau kurang kematian akibat kangker tulang adalah 0.963. Sedangkan, berdasarkan hasil perhitungan menggunakan fungsi `ppois`, proporsi kasus di mana terjadi 4 atau kurang kematian akibat kangker tulang adalah 0.9999999999999999. .
Dari data diatas terdapat perbedaan hasil simulasi dengan hasil perhitungan, namun perbedaan tersebut tidak terlalu signifikan. Hal ini dikarenakan simulasi yang dilakukan hanya sebanyak 1000 kali. Sehingga, semakin banyak simulasi yang dilakukan, maka hasil simulasi akan semakin mendekati hasil perhitungan.
## Soal 3
> Diketahui Nilai X = 3 dan v = 10. Tentukan :
a. Fungsi probabilitas dari distribusi Chi-Square
Fungsi probabilitas dari distribusi Chi-Square dapat dihitung dengan menggunakan rumus berikut ini :
$$f(x) = \frac{1}{2^{\frac{v}{2}}\Gamma(\frac{v}{2})}x^{\frac{v}{2}-1}e^{-\frac{x}{2}}$$
debgan $\Gamma$ adalah fungsi gamma dengan parameter $\frac{v}{2}$.
Untuk x = 3 dan v = 10, maka fungsi probabilitas dari distribusi Chi-Square adalah :
$$f(3) = \frac{1}{2^{\frac{10}{2}}\Gamma(\frac{10}{2})}3^{\frac{10}{2}-1}e^{-\frac{3}{2}}$$
$$f(3) = \frac{1}{2^{5}\Gamma(5)}3^{4}e^{-\frac{3}{2}}$$
$$f(3) = \frac{1}{32\Gamma(5)}81e^{-\frac{3}{2}}$$
$$f(3) = \frac{1}{32(4!)}81e^{-\frac{3}{2}}$$
$$f(3) = \frac{1}{32(24)}81e^{-\frac{3}{2}}$$
$$f(3) = \frac{1}{768}81e^{-\frac{3}{2}}$$
$$f(3) = \frac{81}{768}e^{-\frac{3}{2}}$$
$$f(3) = 0.0235333$$
Untuk menghitung nilai probabilitas dalam R, kita dapat menggunakan fungsi `dchisq`. Berikut ini adalah sintaks untuk menghitung nilai probabilitas dari distribusi Chi-Square :
```r
# Menghitung nilai probabilitas dari distribusi Chi-Square
x = 3
v = 10
# Menghitung nilai probabilitas dari distribusi Chi-Square
prob = dchisq(x, v)
print(paste("Nilai probabilitas dari distribusi Chi-Square adalah", prob))
```
```
"Nilai probabilitas dari distribusi Chi-Square adalah 0.0235332590781547"
```
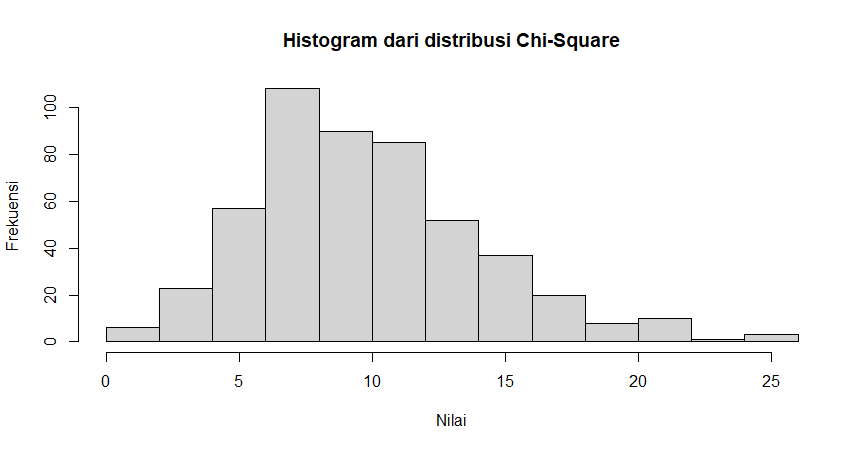
b. Histogram dari distribusi Chi-Square dengan 500 data acak
Untuk menghasilkan sampel acak dari distribusi Chi-Square, kita dapat menggunakan fungsi `rchisq`. Berikut ini adalah sintaks untuk menghasilkan sampel acak dari distribusi Chi-Square :
```r
# Menghasilkan sampel acak dari distribusi Chi-Square
sample = rchisq(500, v)
# Membuat histogram dari distribusi Chi-Square
hist(sample, main = "Histogram dari distribusi Chi-Square", xlab = "Nilai", ylab = "Frekuensi")
```
c. Nilai raatan $\mu$ dan $\sigma^2$ dari distribusi Chi-Square
Untuk menghitung nilai rata-rata dan varians dari distribusi Chi-Square, kita dapat menggunakan fungsi `mean` dan `var`. Berikut ini adalah sintaks untuk menghitung nilai rata-rata dan varians dari distribusi Chi-Square :
```r
# Menghitung nilai rata-rata dari distribusi Chi-Square
mean = mean(sample)
print(paste("Nilai rata-rata dari distribusi Chi-Square adalah", mean))
# Menghitung nilai varians dari distribusi Chi-Square
var = var(sample)
print(paste("Nilai varians dari distribusi Chi-Square adalah", var))
```
```
"Nilai rata-rata dari distribusi Chi-Square adalah 10.1172098876776"
"Nilai varians dari distribusi Chi-Square adalah 19.0266536541921"
```
### Soal 4
>Diketahui data bangkitan acak sebanyak 100 dengan mean = 45 dan sd = 5. Tentukan :
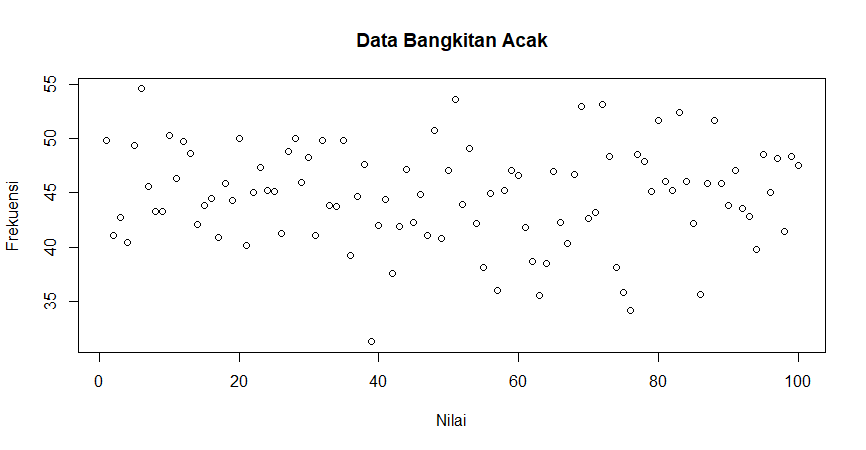
a. Fungsi probabilitas dari distribusi normal $P(X1 <= x <= X2)$, hitung z-scorenya dan plot data bankitan acaknya dalam bentuk grafik. Petunjuk (gunakan fungsi plot)
Untuk menghitung fungsi probabilitas dari distribusi normal, kita dapat menggunakan fungsi `pnorm`. Berikut ini adalah sintaks untuk menghitung fungsi probabilitas dari distribusi normal :
```r
mean = 45
sd = 5
n = 100
# Generate data bangkitan acak
sample = rnorm(n, mean, sd)
x1 = 40
x2 = 50
# Calculate z-score
z1 = (x1 - mean) / sd
z2 = (x2 - mean) / sd
# Menghitung fungsi probabilitas dari distribusi normal
prob = pnorm(z2) - pnorm(z1)
# Plot data bangkitan acak
plot(sample, main = "Data Bangkitan Acak", xlab = "Nilai", ylab = "Frekuensi")
```
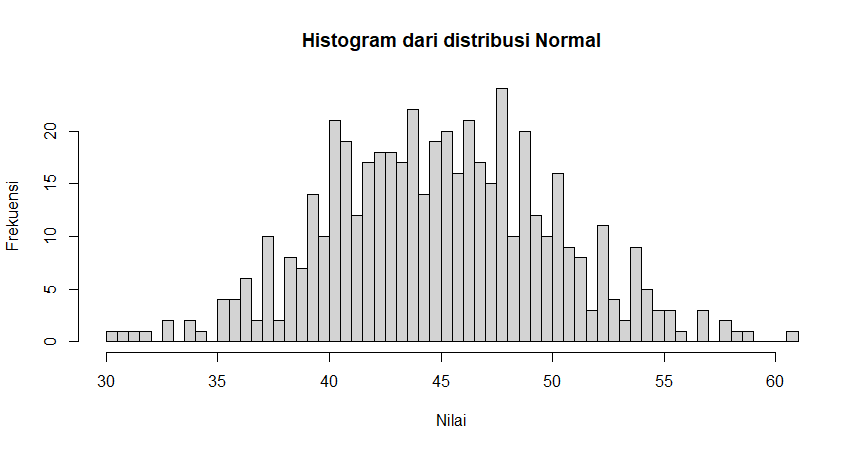
b. Gambarkan histogram dari distribusi Normal dengan breaks 50
Untuk menghasilkan sampel acak dari distribusi normal, kita dapat menggunakan fungsi `rnorm`. Berikut ini adalah sintaks untuk menghasilkan sampel acak dari distribusi normal :
```r
# Menghasilkan sampel acak dari distribusi normal
sample = rnorm(500, mean, sd)
# Membuat histogram dari distribusi normal
hist(sample, breaks = 50, main = "Histogram dari distribusi Normal", xlab = "Nilai", ylab = "Frekuensi")
```
c. Nilai varian dari hasil data bangkitan acak distribusi normal
Untuk menghitung nilai varians dari distribusi normal, kita dapat menggunakan fungsi `var`. Berikut ini adalah sintaks untuk menghitung nilai varians dari distribusi normal :
```r
# Menghitung nilai varians dari distribusi normal
var = var(sample)
print(paste("Nilai varians dari distribusi normal adalah", var))
```
```
"Nilai varians dari distribusi normal adalah 22.5594544435109
```
### Soal 5
>Kerjakanlah menggunakan distribusi T-Student
a. Berapa probabilitas terjadinya suatu peristiwa acak X kurang dari -2,34 dengan 6 derakat kebebasan?
Untuk menghitung nilai probabilitas dari distribusi T-Student, kita dapat menggunakan fungsi `pt`. Berikut ini adalah sintaks untuk menghitung nilai probabilitas dari distribusi T-Student :
```r
x = -2.34
df = 6
# Menghitung nilai probabilitas dari distribusi T-Student
prob = pt(x, df)
print(paste("Nilai probabilitas dari distribusi T-Student adalah", prob))
```
```
"Nilai probabilitas dari distribusi T-Student adalah 0.0289219701335075"
```
b. Berapa probabilitas terjadinya suatu peristiwa acak X lebih dari 1,34 dengan 6 derajat kebebasan?
Untuk menghitung nilai probabilitas dari distribusi T-Student, kita dapat menggunakan fungsi `pt` dengan menambahkan argumen `lower.tail = FALSE` karena kita ingin menghitung nilai probabilitas dari distribusi T-Student yang lebih dari 1,34. Berikut ini adalah sintaks untuk menghitung nilai probabilitas dari distribusi T-Student :
```r
x = 1.34
df = 6
# Menghitung nilai probabilitas dari distribusi T-Student
prob = pt(x, df, lower.tail = FALSE)
print(paste("Nilai probabilitas dari distribusi T-Student adalah", prob))
```
```
"Nilai probabilitas dari distribusi T-Student adalah 0.11437999241044"
```
c. Berapa probabilitas terjadinya suatu peristiwa acak X kurang dari -1,23 atau lebih besar dari 1,23 dengan 3 derajat kebebasan
```r
x1 = -1.23
x2 = 1.23
df = 3
# Menghitung nilai probabilitas dari distribusi T-Student
prob = pt(x1, df) + pt(x2, df, lower.tail = FALSE)
print(paste("Nilai probabilitas dari distribusi T-Student adalah", prob))
```
```
"Nilai probabilitas dari distribusi T-Student adalah 0.306355992486918"
```
d. Berapa probabilitas terjadinya suatu peristiwa acak X berada di antara -0,94 dan 0.94 dengan 14 derajat kebebasan?
```r
x1 = -0.94
x2 = 0.94
# Menghitung nilai probabilitas dari distribusi T-Student
prob = pt(x2, df) - pt(x1, df)
print(paste("Nilai probabilitas dari distribusi T-Student adalah", prob))
```
```
"Nilai probabilitas dari distribusi T-Student adalah 0.583436595003192"
```
e. Berapa nilai t-score dengan 5 derajat kebebasan yang memiliki luasan 0,0333 suatu persegi di bawah kurva dan di sebelah kiri t-score tersebut?
```r
df = 5
prob = 0.0333
# Menghitung nilai t-score
t = qt(prob, df)
print(paste("Nilai t-score adalah", t))
```
```
"Nilai t-score adalah -2.33734195836503"
```
f. Berapa nilai t-score dengan 25 derajat kebebasan yang memiliki luasan 0,125 suatu persegi di bawah kurva dan di sebelah kanan t-score tersebut?
```r
df = 25
prob = 0.125
# Menghitung nilai t-score
t = qt(prob, df, lower.tail = FALSE)
print(paste("Nilai t-score adalah", t))
```
```
"Nilai t-score adalah 1.17771600333508"
```
g. Berapa nilai t-score dengan 11 derajat kebebasan yang memiliki luasan 0.75 suatu persegi di bawah kurva dan di antara t-score tersebut dan negetaif dari nilai t-score tersebut?
```r
df = 11
prob = 0.75
# Menghitung nilai t-score
t = qt(prob, df) - qt(prob, df, lower.tail = FALSE)
print(paste("Nilai t-score adalah", t))
```
```
"Nilai t-score adalah 1.39489065511976"
```
h. Berapa nilai t-score dengan 23 derajat kebebasan yang memiliki luasan 0,0333 suatu persegi di bawah kurva dan di luar interval antara t-score tersebut dan negatif dari nilai t-score tersebut?
```r
df = 23
prob = 0.0333
# Menghitung nilai t-score
t = qt(prob, df) + qt(prob, df, lower.tail = FALSE)
print(paste("Nilai t-score adalah", t))
```