https://github.com/sciml/polychaos.jl

A Julia package to construct orthogonal polynomials, their quadrature rules, and use it with polynomial chaos expansions.
https://github.com/sciml/polychaos.jl

differential-equations julia julia-language orthogonal-polynomials polynomial-chaos-expansions polynomials quadrature quadrature-integration quadrature-rules scientific-machine-learning uncertainty-propagation uncertainty-quantification

Last synced: 7 days ago
JSON representation

A Julia package to construct orthogonal polynomials, their quadrature rules, and use it with polynomial chaos expansions.

• Host: GitHub
• URL: https://github.com/sciml/polychaos.jl
• Owner: SciML
• License: mit
• Created: 2019-01-15T19:14:32.000Z (almost 6 years ago)
• Default Branch: master
• Last Pushed: 2024-10-17T14:09:01.000Z (about 1 month ago)
• Last Synced: 2024-11-06T20:33:39.851Z (14 days ago)
• Topics: differential-equations, julia, julia-language, orthogonal-polynomials, polynomial-chaos-expansions, polynomials, quadrature, quadrature-integration, quadrature-rules, scientific-machine-learning, uncertainty-propagation, uncertainty-quantification
• Language: Julia
• Homepage: https://docs.sciml.ai/PolyChaos/stable/
• Size: 4.13 MB
• Stars: 118
• Watchers: 14
• Forks: 26
• Open Issues: 20
• Metadata Files:
  • Readme: README.md
  • License: LICENSE.md

Awesome Lists containing this project

README

        
# PolyChaos -- Orthogonal Polynomials, Quadrature, and Polynomial Chaos

[![Join the chat at https://julialang.zulipchat.com #sciml-bridged](https://img.shields.io/static/v1?label=Zulip&message=chat&color=9558b2&labelColor=389826)](https://julialang.zulipchat.com/#narrow/stream/279055-sciml-bridged)

[![Global Docs](https://img.shields.io/badge/docs-SciML-blue.svg)](https://docs.sciml.ai/PolyChaos/stable/)

[![codecov](https://codecov.io/gh/SciML/PolyChaos.jl/branch/master/graph/badge.svg)](https://codecov.io/gh/SciML/PolyChaos.jl)

[![Build Status](https://github.com/SciML/PolyChaos.jl/workflows/CI/badge.svg)](https://github.com/SciML/PolyChaos.jl/actions?query=workflow%3ACI)

[![ColPrac: Contributor's Guide on Collaborative Practices for Community Packages](https://img.shields.io/badge/ColPrac-Contributor%27s%20Guide-blueviolet)](https://github.com/SciML/ColPrac)

[![SciML Code Style](https://img.shields.io/static/v1?label=code%20style&message=SciML&color=9558b2&labelColor=389826)](https://github.com/SciML/SciMLStyle)

[![Code DOI](https://zenodo.org/badge/165908711.svg)](https://zenodo.org/badge/latestdoi/165908711)

[![Paper@arXiv](https://img.shields.io/badge/arXiv-2004.03970-green.svg)](https://arxiv.org/abs/2004.03970)

A Julia package to construct orthogonal polynomials, their quadrature rules, and use it with polynomial chaos expansions.

## Tutorials and Documentation

For information on using the package,

[see the stable documentation](https://docs.sciml.ai/PolyChaos/stable/). Use the

[in-development documentation](https://docs.sciml.ai/PolyChaos/dev/) for the version of

the documentation, which contains the unreleased features.

The package requires `Julia 1.3` or newer.

In `Julia` switch to the package manager

```julia

using Pkg

Pkg.add("PolyChaos")

```

This will install PolyChaos and its dependencies.

Once that is done, load the package:

```julia

using PolyChaos

```

That's it.

Let's take a look at a simple example.

We would like to solve the integral

![equation](https://latex.codecogs.com/gif.latex?%5Cint_0%5E1%206%20x%5E5%20%5Cmathrm%7Bd%7Dx.)

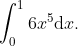
Exploiting the underlying uniform measure, the integration can be done exactly with a 3-point quadrature rule.

```@example mysetup

opq = Uniform01OrthoPoly(3)

integrate(x -> 6x^5, opq)

```

For more information please visit the [documentation](https://docs.sciml.ai/PolyChaos/stable).

## Citing

If you like `PolyChaos.jl`, consider citing our paper

```

@ARTICLE{2020arXiv200403970M,

       author = {{M{\"u}hlpfordt}, Tillmann and {Zahn}, Frederik and {Hagenmeyer}, Veit and {Faulwasser}, Timm},

        title = "{PolyChaos.jl -- A Julia Package for Polynomial Chaos in Systems and Control}",

      journal = {arXiv e-prints},

     keywords = {Electrical Engineering and Systems Science - Systems and Control, Mathematics - Numerical Analysis, Mathematics - Optimization and Control},

         year = 2020,

        month = apr,

          eid = {arXiv:2004.03970},

        pages = {arXiv:2004.03970},

archivePrefix = {arXiv},

       eprint = {2004.03970},

 primaryClass = {eess.SY},

}

```