https://github.com/sigma-py/orthopy
:triangular_ruler: Orthogonal polynomials in all shapes and sizes.
https://github.com/sigma-py/orthopy
chebyshev-polynomials chemistry engineering legendre-polynomials mathematics physics polynomials python quadrature spherical-harmonics zernike-polynomials
Last synced: 2 months ago
JSON representation
:triangular_ruler: Orthogonal polynomials in all shapes and sizes.
- Host: GitHub
- URL: https://github.com/sigma-py/orthopy
- Owner: sigma-py
- Created: 2017-08-20T13:59:37.000Z (over 8 years ago)
- Default Branch: main
- Last Pushed: 2024-02-15T11:37:29.000Z (almost 2 years ago)
- Last Synced: 2025-03-30T01:05:42.707Z (11 months ago)
- Topics: chebyshev-polynomials, chemistry, engineering, legendre-polynomials, mathematics, physics, polynomials, python, quadrature, spherical-harmonics, zernike-polynomials
- Homepage:
- Size: 4.27 MB
- Stars: 185
- Watchers: 8
- Forks: 18
- Open Issues: 8
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
- awesome-scientific-computing - orthopy - Compute orthogonal polynomials efficiently. (Other libraries and tools / Mesh tools)
README
All about orthogonal polynomials.
[](https://pypi.org/project/orthopy)
[](https://pypi.org/pypi/orthopy/)
[](https://github.com/nschloe/orthopy)
[](https://pepy.tech/project/orthopy)
[](https://discord.gg/hnTJ5MRX2Y)
[](https://github.com/nschloe/orthopy)
orthopy provides various orthogonal polynomial classes for
[lines](#line-segment--1-1-with-weight-function-1-x%CE%B1-1-x%CE%B2),
[triangles](#triangle-42),
[disks](#disk-s2),
[spheres](#sphere-u2),
[n-cubes](#n-cube-cn),
[the nD space with weight function exp(-r2)](#nd-space-with-weight-function-exp-r2-enr2)
and more.
All computations are done using numerically stable recurrence schemes. Furthermore, all
functions are fully vectorized and can return results in _exact arithmetic_.
### Installation
Install orthopy [from PyPI](https://pypi.org/project/orthopy/) with
```
pip install orthopy
```
### How to get a license
Licenses for personal and academic use can be purchased
[here](https://buy.stripe.com/aEUg1H38OgDw5qMfZ3).
You'll receive a confirmation email with a license key.
Install the key with
```
plm add
```
on your machine and you're good to go.
For commercial use, please contact support@mondaytech.com.
### Basic usage
The main function of all submodules is the iterator `Eval` which evaluates the series of
orthogonal polynomials with increasing degree at given points using a recurrence
relation, e.g.,
```python
import orthopy
x = 0.5
evaluator = orthopy.c1.legendre.Eval(x, "classical")
for _ in range(5):
print(next(evaluator))
```
```python
1.0 # P_0(0.5)
0.5 # P_1(0.5)
-0.125 # P_2(0.5)
-0.4375 # P_3(0.5)
-0.2890625 # P_4(0.5)
```
Other ways of getting the first `n` items are
```python
evaluator = Eval(x, "normal")
vals = [next(evaluator) for _ in range(n)]
import itertools
vals = list(itertools.islice(Eval(x, "normal"), n))
```
Instead of evaluating at only one point, you can provide any array for `x`; the
polynomials will then be evaluated for all points at once. You can also use sympy for
symbolic computation:
```python
import itertools
import orthopy
import sympy
x = sympy.Symbol("x")
evaluator = orthopy.c1.legendre.Eval(x, "classical")
for val in itertools.islice(evaluator, 5):
print(sympy.expand(val))
```
```
1
x
3*x**2/2 - 1/2
5*x**3/2 - 3*x/2
35*x**4/8 - 15*x**2/4 + 3/8
```
All `Eval` methods have a `scaling` argument which can have three values:
- `"monic"`: The leading coefficient is 1.
- `"classical"`: The maximum value is 1 (or (n+alpha over n)).
- `"normal"`: The integral of the squared function over the domain is 1.
For univariate ("one-dimensional") integrals, every new iteration contains one function.
For bivariate ("two-dimensional") domains, every level will contain one function more
than the previous, and similarly for multivariate families. See the tree plots below.
### Line segment (-1, +1) with weight function (1-x)α (1+x)β
|  |
|  |
|  |
|
| :---------------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------------: |
| Legendre | Chebyshev 1 | Chebyshev 2 |
Jacobi, Gegenbauer (α=β), Chebyshev 1 (α=β=-1/2), Chebyshev 2 (α=β=1/2), Legendre
(α=β=0) polynomials.
```python
import orthopy
orthopy.c1.legendre.Eval(x, "normal")
orthopy.c1.chebyshev1.Eval(x, "normal")
orthopy.c1.chebyshev2.Eval(x, "normal")
orthopy.c1.gegenbauer.Eval(x, "normal", lmbda)
orthopy.c1.jacobi.Eval(x, "normal", alpha, beta)
```
The plots above are generated with
```python
import orthopy
orthopy.c1.jacobi.show(5, "normal", 0.0, 0.0)
# plot, savefig also exist
```
Recurrence coefficients can be explicitly retrieved by
```python
import orthopy
rc = orthopy.c1.jacobi.RecurrenceCoefficients(
"monic", # or "classical", "normal"
alpha=0, beta=0, symbolic=True
)
print(rc.p0)
for k in range(5):
print(rc[k])
```
```
1
(1, 0, None)
(1, 0, 1/3)
(1, 0, 4/15)
(1, 0, 9/35)
(1, 0, 16/63)
```
### 1D half-space with weight function xα exp(-r)

(Generalized) Laguerre polynomials.
```python
evaluator = orthopy.e1r.Eval(x, alpha=0, scaling="normal")
```
### 1D space with weight function exp(-r2)

Hermite polynomials come in two standardizations:
- `"physicists"` (against the weight function `exp(-x ** 2)`
- `"probabilists"` (against the weight function `1 / sqrt(2 * pi) * exp(-x ** 2 / 2)`
```python
evaluator = orthopy.e1r2.Eval(
x,
"probabilists", # or "physicists"
"normal"
)
```
#### Associated Legendre "polynomials"

Not all of those are polynomials, so they should really be called associated Legendre
_functions_. The kth iteration contains _2k+1_ functions, indexed from
_-k_ to _k_. (See the color grouping in the above plot.)
```python
evaluator = orthopy.c1.associated_legendre.Eval(
x, phi=None, standardization="natural", with_condon_shortley_phase=True
)
```
### Triangle (_T2_)

orthopy's triangle orthogonal polynomials are evaluated in terms of [barycentric
coordinates](https://en.wikipedia.org/wiki/Barycentric_coordinate_system), so the
`X.shape[0]` has to be 3.
```python
import orthopy
bary = [0.1, 0.7, 0.2]
evaluator = orthopy.t2.Eval(bary, "normal")
```
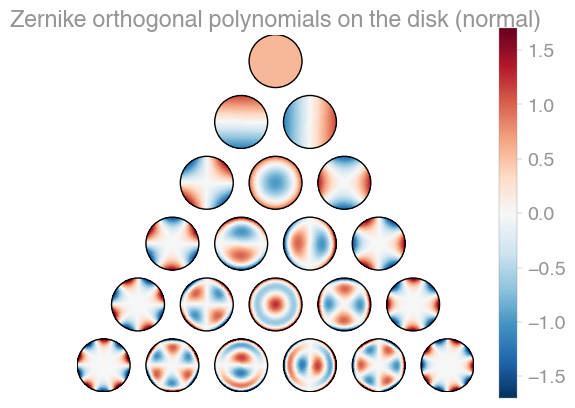
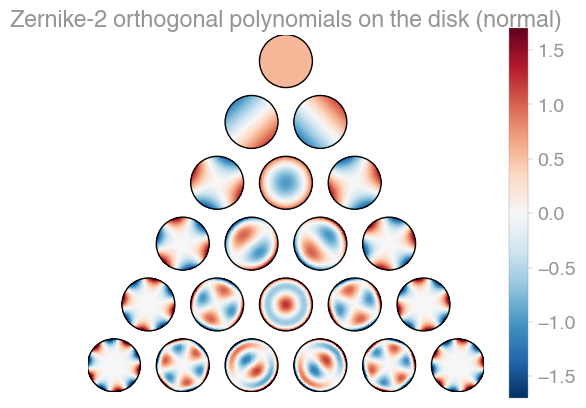
### Disk (_S2_)
|  |
|  |
|  |
|
| :------------------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------------------: |
| Xu | [Zernike](https://en.wikipedia.org/wiki/Zernike_polynomials) | Zernike 2 |
orthopy contains several families of orthogonal polynomials on the unit disk: After
[Xu](https://arxiv.org/abs/1701.02709),
[Zernike](https://en.wikipedia.org/wiki/Zernike_polynomials), and a simplified version
of Zernike polynomials.
```python
import orthopy
x = [0.1, -0.3]
evaluator = orthopy.s2.xu.Eval(x, "normal")
# evaluator = orthopy.s2.zernike.Eval(x, "normal")
# evaluator = orthopy.s2.zernike2.Eval(x, "normal")
```
### Sphere (_U3_)
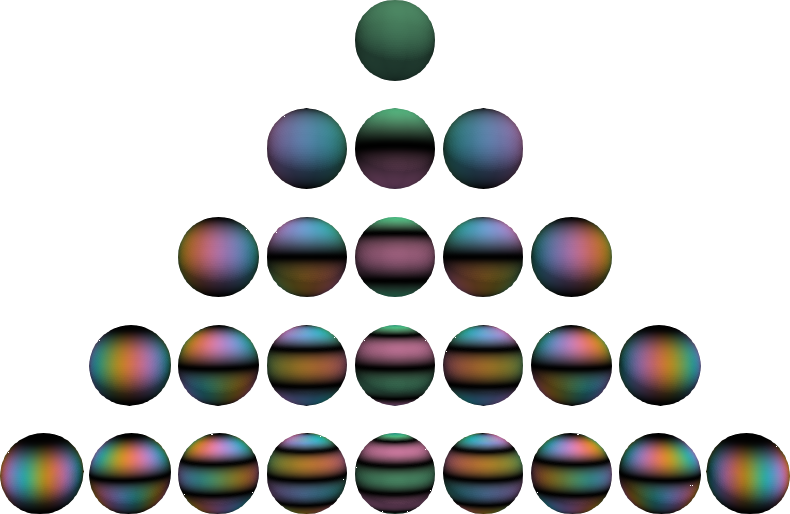
Complex-valued _spherical harmonics,_ (black=zero, green=real positive,
pink=real negative, blue=imaginary positive, yellow=imaginary negative). The
functions in the middle are real-valued. The complex angle takes _n_ turns on
the nth level.
```python
evaluator = orthopy.u3.EvalCartesian(
x,
scaling="quantum mechanic" # or "acoustic", "geodetic", "schmidt"
)
evaluator = orthopy.u3.EvalSpherical(
theta_phi, # polar, azimuthal angles
scaling="quantum mechanic" # or "acoustic", "geodetic", "schmidt"
)
```
### _n_-Cube (_Cn_)
|  |
| 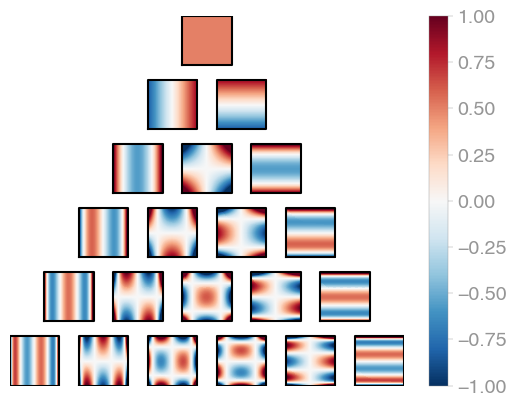 |
|  |
|
| :---------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------: | :---------------------------------------------------------------------------------------: |
| C1 (Legendre) | C2 | C3 |
Jacobi product polynomials.
All polynomials are normalized on the n-dimensional cube. The dimensionality is
determined by `X.shape[0]`.
```python
evaluator = orthopy.cn.Eval(X, alpha=0, beta=0)
values, degrees = next(evaluator)
```
### nD space with weight function exp(-r2) (_Enr2_)
|  |
| 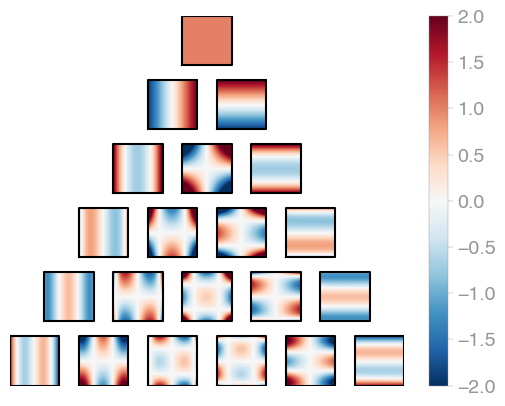 |
|  |
|
| :-----------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------------: |
| _E1r2_ | _E2r2_ | _E3r2_ |
Hermite product polynomials.
All polynomials are normalized over the measure. The dimensionality is determined by
`X.shape[0]`.
```python
evaluator = orthopy.enr2.Eval(
x,
standardization="probabilists" # or "physicists"
)
values, degrees = next(evaluator)
```
### Other tools
- Generating recurrence coefficients for 1D domains with
[Stieltjes](https://github.com/nschloe/orthopy/wiki/Generating-1D-recurrence-coefficients-for-a-given-weight#stieltjes),
[Golub-Welsch](https://github.com/nschloe/orthopy/wiki/Generating-1D-recurrence-coefficients-for-a-given-weight#golub-welsch),
[Chebyshev](https://github.com/nschloe/orthopy/wiki/Generating-1D-recurrence-coefficients-for-a-given-weight#chebyshev), and
[modified
Chebyshev](https://github.com/nschloe/orthopy/wiki/Generating-1D-recurrence-coefficients-for-a-given-weight#modified-chebyshev).
- The the sanity of recurrence coefficients with test 3 from [Gautschi's article](https://doi.org/10.1007/BF02218441):
computing the weighted sum of orthogonal polynomials:
```python
orthopy.tools.gautschi_test_3(moments, alpha, beta)
```
- [Clenshaw algorithm](https://en.wikipedia.org/wiki/Clenshaw_algorithm) for
computing the weighted sum of orthogonal polynomials:
```python
vals = orthopy.c1.clenshaw(a, alpha, beta, t)
```
### Relevant publications
- [Robert C. Kirby, Singularity-free evaluation of collapsed-coordinate orthogonal polynomials, ACM Transactions on Mathematical Software (TOMS), Volume 37, Issue 1, January 2010](https://doi.org/10.1145/1644001.1644006)
- [Abedallah Rababah, Recurrence Relations for Orthogonal Polynomials on Triangular Domains, MDPI Mathematics 2016, 4(2)](https://doi.org/10.3390/math4020025)
- [Yuan Xu, Orthogonal polynomials of several variables, arxiv.org, January 2017](https://arxiv.org/abs/1701.02709)
