Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/stevana/hot-swapping-state-machines2
Experiment with hot swapping pipelined state machines
https://github.com/stevana/hot-swapping-state-machines2
Last synced: 9 days ago
JSON representation
Experiment with hot swapping pipelined state machines
- Host: GitHub
- URL: https://github.com/stevana/hot-swapping-state-machines2
- Owner: stevana
- License: bsd-2-clause
- Created: 2024-02-03T14:33:52.000Z (9 months ago)
- Default Branch: main
- Last Pushed: 2024-03-07T13:30:50.000Z (8 months ago)
- Last Synced: 2024-03-08T10:58:17.037Z (8 months ago)
- Language: Haskell
- Homepage:
- Size: 325 KB
- Stars: 1
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- Changelog: CHANGELOG.md
- License: LICENSE
Awesome Lists containing this project
README
# Towards zero-downtime upgrades of stateful systems
## Motivation
Most deployed programs need to be upgraded at some point. The reasons vary from
adding new features to patching a bug and potentially fixing a broken state.
Even though upgrades are an essential part of software development and
maintenance, programming languages tend to not help the programmer deal with
them in any way.
The situation reminds me of a remark made by Barbara Liskov about deployment of
software (which is related to upgrades) in her Turing award
[lecture](https://youtu.be/qAKrMdUycb8?t=3058) (2009):
> "There’s a funny disconnect in how we write distributed programs. You write
> your individual modules, but then when you want to connect them together
> you’re out of the programming language and into this other world. Maybe we
> need languages that are a little bit more complete now, so that we can write
> the whole thing in the language."
There's one exception, that I know of, where upgrades are talked about from
within the language: Erlang/OTP. In OTP there's a library construct called
[*release*](https://www.erlang.org/doc/design_principles/release_structure),
which can be used to perform up- and downgrades. Furthermore, these up- and
downgrades can hot swap the running code resulting in zero-downtime and no
interruption of the service of connected clients.
If you haven't seen Erlang's hot swapping feature before, then you might want to
have a look at the classic [Erlang the
movie](https://www.youtube.com/watch?v=xrIjfIjssLE), which contains a
telecommunications example of this. If you prefer reading over watching, then
I've written an earlier
[post](https://stevana.github.io/hot-code_swapping_a_la_erlang_with_arrow-based_state_machines.html)
which starts off by explaining a REPL session which performs an upgrade (my
example isn't nearly as cool as in the movie though).
What is it that Erlang's releases and hot swapping facilities do? Can we steal
those ideas and build upon them? These are the main questions that motivated me
in writing this post.
Let's take a step back, ignoring Erlang for a moment, and ask ourselves: what
would good support for upgrades look like?
* Zero-downtime: seamless, don't interrupt existing client connections or
sessions;
* If there's any state then migrate it in a type-safe way;
* Backwards and forwards compatibility: old clients should be able to talk to
newer servers, and newer clients should be able to talk to old servers;
* Atomicity: upgrades either succeed, or fail and rollback any changes;
* Downgrades: even if an upgrade succeeds we might want to rollback to an
earlier version.
In the rest of this post I'd like to explore how we can achieve some of this.
## Terminology
Having defined some desirable characteristics of upgrades, let's move on to
defining what we mean by upgrades.
There are two notions I'd like clarify: what kind of software systems the
upgrades are targeting, and then how we represent programs and their upgrades.
### Software systems
There's different kinds of software systems one might want to upgrade.
1. Client-only, e.g. a compiler, editor, or some command line utility which
runs locally on your computer and doesn't interact with any server.
Downtime is typically not a problem, and the state of the program is
typically saved to disk. The operating system's package manager typically
takes care of the upgrades, with minimal user involvement. However there
are situations where one might like to perform an upgrade without first
terminating the old version of a client-only application, e.g. the
fix-and-continue debugging
[workflow](https://lispcookbook.github.io/cl-cookbook/debugging.html#resume-a-program-execution-from-anywhere-in-the-stack)
from Lisp and Smalltalk, [live coding
music](https://en.wikipedia.org/wiki/TidalCycles), or when working with
large data sets, e.g. in
[bioinformatics](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1386713/);
2. Client-server applications where the target of the upgrade is a *stateless*
component of the server, e.g. a front-end or a REST API. The stateless
components typically retrieve the state they need to service a request from
a stateful component, e.g. a database, but they don't maintain any state of
their own, which makes stateless components easier to upgrade. A common
strategy is to stick a load balancer in-front of the stateless
component(s), spin up the new version of the component while keeping the
old version around, and then (slowly) migrate traffic over to the new
version. Notice that this wouldn't necessarily work if there was state in
the components, as then the state of the old and new versions of the
components might diverge and potentially have unexpected results;
3. Client-server applications where the target of the upgrade is a *stateful*
component of the server, e.g. a database or a service with a stateful
protocol like FTP. Databases were designed for supporting upgrades, with
features like schema migrations and replication. The high-level idea would
be to spin up the new version, take a snapshot of the old database, start
logically replicating all new requests from the old to the new database
while also restoring the snapshot to the new database, once the new
database has caught up, we can switch over and tear down the old database.
Depending on the volume of the database and the rate of new traffic this
can still be a difficult operation.
A service like FTP, where once the user is connected they can "move around"
by e.g. changing the working directory and list the contents of the current
working directory, are typically not possible to upgrade without downtime.
The problem is that the response of one command depends on the history of
previous commands in that user sessions, and this state is transient. If
you think FTP is a silly protocol (it's), then consider the similarly
stateful POSIX filesystem API, with its file handles that can be opened,
read, written, and closed;
4. Distributed stateful systems, e.g. a distributed key-value database. This
is similar to the above, but the replication of data is performed all the
time rather than only at the moment an upgrade is performed. The
disadvantage is that we need more hardware and bandwidth, but on the other
hand it makes upgrades much easier. Distributed systems can typically
tolerate and repair some amount of faulty replicas, which allows for
rolling upgrades where we replace one of the server components at the time;
5. There's also [local-first](https://www.inkandswitch.com/local-first/)
systems, which are different to all the above. I've not had a chance to think
about upgrades in that context, so I won't talk about them any further.
In this post I'd like to focus on upgrading stateful systems, like
non-distributed databases and stateful services like FTP or filesystems.
Stateful systems arguably have the worst upgrade path of the ones listed above,
making them more interesting to work on. That said I hope that the techniques
can be used to simplify upgrades in the other kinds of systems too, and
potentially enabling other possibilities like better debugging experience and
live coding.
### Programs and their upgrades
Having defined what kind of systems we'd like to upgrade, let's turn our
attention to how we can represent programs and their upgrades.
We could choose to use the syntax of a specific programming language to
represent programs, but programming languages tend to be too big and
complicated. Or, we could be general and represent programs as λ-calculus terms
or equivalently Turing machines, but that would be too clumsy and too low-level.
A happy middle ground, which is easy to implement in any programming language
while at the same time expressive enough to express any algorithm at a desired
level of abstraction, is the humble state machine[^1]. There are different ways
to define state machines, we'll go for a definition which is a simple function
from some input and a state to a pair of some output and a new state:
```
input -> state -> (state, output)
```
where inputs, states and outputs are algebraic datatypes (records/structs and
tagged unions).
To make things concrete, let's consider an example where we represent a counter
as a state machine. One way to define such a state machine is to use the enum
`{ReadCount, IncrCount}` as input, set the state to be an integer and the output
to be a tagged union where in the read case we return an integer and in the
increment case we return an acknowledgment (unit or void type). Given these
types, the state machine function of the counter can be defined as follows (in
Python):
```python
def counter(input: Input, state: int) -> (int, int | None):
match input:
case Input.ReadCount: return (state, state)
case Input.IncrCount: return (state + 1, None)
```
Assuming our programs are such state machines, what would it mean to upgrade
them? I think this is where having a simple representation of programs where all
of the state is explicit starts to shine. By merely looking at the function type
of a state machine, we can see that it would make sense to be able to:
1. Extend the input type with more cases, e.g. a `ResetCount` which sets the
new state to `0`;
2. Refine an existing output with more data, e.g. we could return the old
count when we increment;
3. Extending the state, e.g. we could add a boolean to the state which
determines if we should increment by +1 or -1 (i.e. decrementing);
4. Refine an existing input, e.g. make `IncrCount` have an integer value
associated with it which determines by how much we want to increment.
I don't know if the above list complete, but it's a start.
If we go back to the list of criteria for good upgrade support, we can see how
some of the items there are more tangible now.
For example, typed state migrations means that if we change the state type from
`state` to `state'` then when we migrate to old to the new state using a
function of type `state -> state'`.
Similarly, what it means to support backwards compatibility is more clear now.
Imagine we upgrade from a server state machine:
```
input -> state -> (output, state)
```
to a new version that has the following type:
```
input' -> state' -> (output', state')
```
What would it take to still be able to serve old clients which make requests
using the old `input` type? If we had a function from `input -> input'` we could
upgrade the request, feed it to the new state machine and get an `output'` back,
we then see that we'd also need a way to downgrade the output, i.e. a function
`output' -> output`[^2].
Forward compatibility, i.e. an upgraded client sends an `input'` to a server
which haven't been upgraded yet (i.e. expects `input`), is a bit more tricky,
but again at least we can now start to be able to talk about these things in a
more concrete way.
One last thing with regard to how to represent programs. Our state machines run
entirely sequentially, which is a problem if we want to implement servers that
can handle more than one client at the time. A simple way adding parallelism is
make it possible to construct pipelines of state machines, where the state
machines run in parallel. Picture the state machines as processing stages on a
conveyor belt.
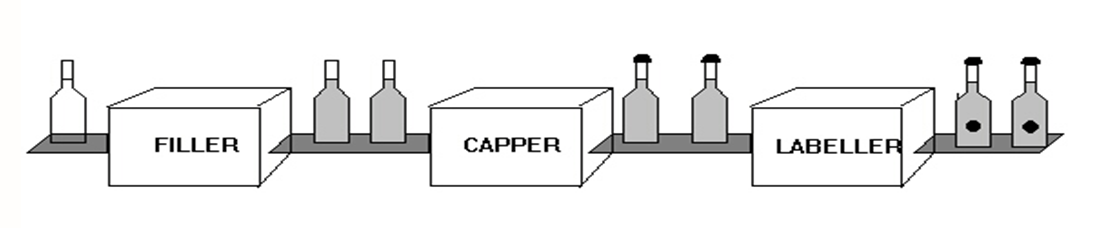
The conveyor belt in our case, i.e. our pipeline, will be queues which connect
the state machines.
A typical TCP-based service can then be composed of a pipeline that:
1. Accepts new connections/sockets from a client;
2. Waits for some of the accepted sockets to be readable (this requires some
`select/poll/io_uring`-like constructs);
3. `recv` the bytes of a request;
4. Deserialise the request bytes into an input;
5. Process the input using the a state machine to produce an output
(potentially reading and writing to disk);
6. Serialise the output into a response in bytes;
7. Wait for the socket to be writable;
8. `send` the response bytes back to the client and close the socket.
Each of these stages could be a state machine which runs in parallel with all
the other stages. Structuring services in this pipeline fashion was
[advocated](https://www.youtube.com/watch?v=U3eo49nVxcA&t=1949s) by the late Jim
Gray and more recently Martin Thompson et al have
[been](https://www.youtube.com/watch?v=qDhTjE0XmkE) giving
[talks](https://www.youtube.com/watch?v=_KvFapRkR9I) using a similar approach.
If a stage is slow, we can shard (or partition, using Jim's terminology) it by
dedicating another CPU/core to that stage and have even numbered requests to one
CPU/core while odd numbered requests go to the other. That way we effectively
double the throughput, without breaking determinism.
Let me just leave you with one final image. I like to think of state machines on
top of pipelines as a limited form of actors or Erlang processes (`gen_server`s
more precisely) that cannot send messages to which other process they like
(graph-like structure), but rather only downstream (DAG-like structure)[^3].
## Implementation
I hope that I've managed to convey what I'd like to do, why and where my
inspiration is coming from.
Next I'd like to make things more concrete with some code. But first I'd like to
apologies for my choice of using Haskell. I know it's a language that not that
many people are comfortable with, but its advanced type system (GADTs in
particular) helps me express things more cleanly. If anything isn't clear, feel
free to ask, I'm happy to try to explain things in simpler terms. Also if anyone
knows how to express this without GADTs, while retaining type safety, then
please let me know. The code doesn't add anything new to our previous
discussion, merely validates that at least some of it can be implemented, so
even if you can't follow everything you won't be missing out on anything
important.
A few notes on the implementation:
* To keep things simple we'll only implement linear pipelines. Each stage of the
pipeline runs in parallel with all other stages, thus giving us pipelining
parallelism à la assembly lines;
* The transformation at each stage is done via a state machine. The syntax of
state machines needs to be easily serialisable, so that we can send upgrades
over the wire;
* The remote end will need to deserialise and typecheck the receiving code in
order to assure that it's compatible with the already deployed code.
In the rest of this section we'll try to fleshing out details of the above.
### State machines
Typed state machines are represented using a datatype parametrised by the state,
`s`, and indexed by its input type, `a`, and output type `b`[^4]. For example
the `Id`entity state machine has the same input and output type, while if we
want to `Compose` to state machines then output type of the first needs to be
the same as the input type of the second, and so on.
```haskell
data T s a b where
-- Identity and composition.
Id :: T s a a
Compose :: T s b c -> T s a b -> T s a c
-- Introducing and incrementing integers.
Int :: Int -> T s () Int
Incr :: T s Int Int
-- Mapping over sum types.
Case :: T s a c -> T s b d -> T s (Either a b) (Either c d)
-- Read and update the state.
Get :: T s () s
Put :: T s s ()
-- Converting values from and to strings.
Read :: Read a => T s String a
Show :: Show a => T s a String
-- Forward composition.
(>>>) :: T s a b -> T s b c -> T s a c
f >>> g = g `Compose` f
```
### Example
To keep things concrete let's reimplement the counter example from above.
```haskell
type InputV1 = Either () ()
type OutputV1 = Either Int ()
pattern ReadCountV1 :: InputV1
pattern ReadCountV1 = Left ()
pattern IncrCountV1 :: InputV1
pattern IncrCountV1 = Right ()
counterV1 :: T Int String String
counterV1 = Read >>> counterV1' >>> Show
where
counterV1' :: T Int InputV1 OutputV1
counterV1' = Get `Case` (Get >>> Incr >>> Put)
```
Notice how the two operations' inputs and outputs are represented with an
`Either` over which the `Case` operates.
### Semantics
We can interpret our typed state machines in terms of the `State` monad as
follows.
```haskell
runT :: T s a b -> a -> s -> (b, s)
runT f x s = runState (eval f x) s
eval :: T s a b -> a -> State s b
eval Id = return
eval (Compose g f) = eval g <=< eval f
eval (Int i) = return . const i
eval Incr = return . (+ 1)
eval (Case f g) = either (fmap Left . eval f) (fmap Right . eval g)
eval Get = const get
eval Put = put
eval Read = return . read
eval Show = return . show
```
Using the above interpreter we can run our example from before.
```haskell
> runT counterV1 (show ReadCountV1) 0
("Left 0",0)
> runT counterV1 (show IncrCountV1) 0
("Right ()",1)
> runT counterV1 (show ReadCountV1) 1
("Left 1",1)
```
These runs only step the counter by one input at the time, things get more
interesting when state machines get streams of inputs via pipelines.
### Pipelines
Pipelines are represented by a type similar to that for typed state machines,
it's also indexed by the input and output types.
We can picture a pipeline as a conveyor belt with state machines operating on
the items passing through.
```haskell
data P a b where
IdP :: P a a
(:>>>) :: Typeable b => P a b -> P b c -> P a c
SM :: Typeable s => Name -> s -> T s a b -> P a b
type Name = String
```
Notice how the state type of the state machines is existentially quantified,
meaning each state machine can have its own state.
### Deployment
Pipelines can be deployed. Each state machine will be spawned on its own thread,
meaning that all state machines run in parallel, and they will be connected via
queues.
Given a pipeline `P a b` and an input `Queue (Msg a)` we get an output `Queue
(Msg b)`:
```haskell
deploy :: forall a b. (Typeable a, Typeable b)
=> P a b -> Queue (Msg a) -> IO (Queue (Msg b))
```
where `Msg` is defined as follows.
```haskell
data Msg a
= Item (Maybe Socket) a
| Upgrade (Maybe Socket) Name UpgradeData_
...
```
Think of `Msg a` as small wrapper around `a` which might contain a client socket
(so that we know where to send the reply), or an upgrade. Upgrades are targeting
a specific state machine in our pipeline, that's what the `Name` parameter is
for, and they also carry an untyped `UpgradeData_` payload which will come back
to shortly.
Given the above we can define deployment of pipelines as follows (I'll explain
each case below the code).
```haskell
deploy IdP q = return q
deploy (f :>>> g) q = deploy g =<< deploy f q
deploy (SM name s0 f0) q = do
q' <- newQueue
let go :: Typeable s => s -> T s a b -> IO ()
go s f = do
m <- readQueue q
case m of
Item msock i -> do
let (o, s') = runT f i s
writeQueue q' (Item msock o)
go s' f
Upgrade msock name' ud
| name /= name' -> do
writeQueue q' (Upgrade msock name' ud)
go s f
| otherwise ->
case typeCheckUpgrade f ud of
Just (UpgradeData (f' :: T t' a b) (g :: T () s t')) -> do
let (t', ()) = runT g s ()
case cast t' of
Just s' -> go s' f'
Nothing -> go s f
Nothing -> go s f
...
_pid <- forkIO (go s0 f0)
return q'
```
The identity pipeline simply returns the input queue. We deploy compositions of
pipelines by deploying the components and connecting the queues. Deploying state
machines is the interesting part.
When we deploy state machines, we first create a new queue which will hold the
outputs, we then fork a new thread which reads from the input queue and writes
to this new output queue, and finally we return the output queue. When reading
from the input queue there're two cases:
1. We can either get a regular `Item` in which case we step our state machine
using the `runT` function to obtain an output and a new state, we write the
output to the output queue and continue processing with the new state;
2. Or, if the `Msg` is an `Upgrade` we first check if the upgrade is targeting
this state machine by checking if the names match, if not we simply pass it
further downstream. If the names to match then we try to typecheck the
untyped `UpgradeData_`. If the typechecking succeeds, we'll get a new state
machine and a state migration function, which allows us to migrate the
current state and continue processing with the new state machine.
Next let's have a look at how upgrades are represented and typechecked.
### Upgrades
Upgrades are sent over the wire in a serialised format and deserialised at the
other end, so they need to be plain first-order data.
This means we can't merely send over our typed state machine type `t :: T s a
b`, or rather the receiver will have to reconstruct the type information. If
this sounds strange, the perhaps easiest way to convince yourself is to imagine
you receive `show t` and now you want to reconstruct `t`. When you call `read
(show t)` you need to annotate it with what type to read into, and that's the
problem: at this point you don't have the type annotation `T s a b`.
So the plan around this is to introduce a plain first-order datatype for
upgrades, which can easily be serialised and deserialised, and then use
*typechecking* to reconstruct the type information.
```haskell
data UpgradeData_ = UpgradeData_
{ oldState :: Ty_
, newState :: Ty_
, newInput :: Ty_
, newOutput :: Ty_
, newStateMachine :: U
, stateMigration :: U
}
deriving (Show, Read)
```
We can to typecheck the above untyped upgrade into the following typed version.
```haskell
data UpgradeData s a b = forall s'. Typeable s' =>
UpgradeData (T s' a b) (T () s s')
```
The way typechecking for upgrades work is basically the user needs to provide
the untyped types of the state, input and output types of the new state machine
as well as the state migration function, from the untyped types we can infer the
typed types which we then typecheck the new state machine and migration function
against.
```haskell
typeCheckUpgrade :: forall s a b. (Typeable s, Typeable a, Typeable b)
=> T s a b -> UpgradeData_ -> Maybe (UpgradeData s a b)
typeCheckUpgrade _f (UpgradeData_ t_ t'_ a'_ b'_ f_ g_) =
case (inferTy t_, inferTy t'_, inferTy a'_, inferTy b'_) of
(ETy (t :: Ty t), ETy (t' :: Ty t'), ETy (a' :: Ty a'), ETy (b' :: Ty b')) -> do
Refl <- decT @a @a'
Refl <- decT @b @b'
Refl <- decT @s @t
f <- typeCheck f_ t' a' b'
g <- typeCheck g_ TUnit t t'
return (UpgradeData f g)
```
Where untyped types are defined as follows:
```haskell
data Ty_
= UTUnit
| UTInt
| UTBool
| UTString
| UTPair Ty_ Ty_
| UTEither Ty_ Ty_
```
and typed types as follows:
```haskell
data Ty a where
TUnit :: Ty ()
TInt :: Ty Int
TBool :: Ty Bool
TString :: Ty String
TPair :: Ty a -> Ty b -> Ty (a, b)
TEither :: Ty a -> Ty b -> Ty (Either a b)
...
```
and the way we infer typed types from the untyped ones is done as follows:
```haskell
data ETy where
ETy :: Typeable a => Ty a -> ETy
inferTy :: Ty_ -> ETy
inferTy UTUnit = ETy TUnit
inferTy UTInt = ETy TInt
inferTy UTBool = ETy TBool
inferTy UTString = ETy TString
inferTy (UTPair ua ub) = case (inferTy ua, inferTy ub) of
(ETy a, ETy b) -> ETy (TPair a b)
inferTy (UTEither ua ub) = case (inferTy ua, inferTy ub) of
(ETy a, ETy b) -> ETy (TEither a b)
```
Now the only piece missing is untyped state machines and how to typecheck those
into typed ones.
```haskell
typeCheck :: U -> Ty s -> Ty a -> Ty b -> Maybe (T s a b)
data U
= IdU
| ComposeU U U
| IntU Int
| CaseU U U
| IncrU
| GetU
| PutU
| ReadU Ty_
| ShowU Ty_
```
I'll spare you from the
[details](https://github.com/stevana/hot-swapping-state-machines2/blob/main/src/TypeCheck/StateMachine.hs),
but the main ingredient is to use the `Data.Typeable` instances to check if the
types match up, similarly to how it was done above in `typeCheckUpgrade`.
### Sources and sinks
Almost there. When we deploy a pipeline `P a b` we need to provide a `Queue (Msg
a)` and get a `Queue (Msg b)`, what are we supposed to do with those queues? We
could manually feed them with items, but for convenience it's nice to have some
basic reusable adapters that we can connect these "garden hoses" to.
We call something that provides an input queue a `Source` and something that
consumes an output queue a `Sink`. Useful sources and sinks include
stdin/stdout, files, and TCP streams.
We can then implement a run function with the following type:
```haskell
run :: (Typeable a, Typeable b)
=> Source a -> Codec (Msg a) (Msg b) -> P a b -> Sink b r -> IO r
```
Where `Codec a b` contains a deserialiser from `ByteString` to `Maybe a` and a
serialiser from `b` to `ByteString`. We need this because our sources and sinks
produce and consume `ByteString`s.
### Remote upgrades
Putting it all together we can now create a TCP server for our counter:
```haskell
run (FromTCP "127.0.0.1" 3000) readShowCodec (SM "counter" 0 counterV1) ToTCP
```
If we run the above in a REPL, then from another terminal we can interact with
the server as follows.
```bash
# Get the current state of the counter.
$ echo 'Item "Left ()"' | nc 127.0.0.1 3000
Item "Left 0"
# Increment the counter.
$ echo 'Item "Right ()"' | nc 127.0.0.1 3000
Item "Right ()"
# Read the counter again.
$ echo 'Item "Left ()"' | nc 127.0.0.1 3000
Item "Left 1"
```
In order to make life a bit easier for ourselves, we can implement a simple TCP
client in Haskell and use from another REPL to achieve the same result.
```haskell
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV1))
```
```
Item "Left 0" -- The initial value of the counter is 0.
Item "Right ()" -- Two increments.
Item "Right ()"
Item "Left 2" -- The value is now 2
```
At this point, let's imagine we want to add a reset feature to our counter.
Reset takes no argument and returns nothing, so we use the unit type in both the
input and output types.
```haskell
type InputV2 = Either () InputV1
type OutputV2 = Either () OutputV1
pattern ResetCountV2 :: InputV2
pattern ResetCountV2 = Left ()
pattern ReadCountV2 :: InputV2
pattern ReadCountV2 = Right ReadCountV1
pattern IncrCountV2 :: InputV2
pattern IncrCountV2 = Right IncrCountV1
```
The state machine looks the same, except for the first `Case` where we update the
state to be `0`, thus resetting the counter.
```haskell
counterV2 :: T Int String String
counterV2 = Read >>> counterV2' >>> Show
where
counterV2' :: T Int InputV2 OutputV2
counterV2' =
(Int 0 >>> Put) `Case`
Get `Case`
(Get >>> Incr >>> Put)
```
Back in our REPL we can now do the upgrade, by sending over a type `erase`d
version of `counterV2`.
```haskell
let msg :: Msg ()
msg = Upgrade Nothing "counter"
(UpgradeData_ UTInt UTInt UTString UTString (erase counterV2) (erase Id))
nc "127.0.0.1" 3000 msg
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV2))
nc "127.0.0.1" 3000 (Item Nothing (show ResetCountV2))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV2))
```
Which yields the following annotated output.
```
UpgradeSucceeded "counter"
Item "Right (Left 2)" -- The counter's state is preserved by the upgrade.
Item "Left ()" -- Reset the counter.
Item "Right (Left 0)" -- The value is back to 0.
```
As a final example of an upgrade, let's do a more interesting state migration.
Let's say we want to add a boolean to the state which determines if `IncrCount`
should add by `1` or `-1` (i.e. decrement). This boolean can be toggled by the
user using a new operation, while the signatures of the other operations stay
the same as before.
```haskell
type InputV3 = Either () InputV2
type OutputV3 = Either () OutputV2
pattern ToggleCountV3 :: InputV3
pattern ToggleCountV3 = Left ()
pattern ReadCountV3, IncrCountV3, ToggleCountV3 :: InputV3
```
In order to implement the toggle operation we need to extend the syntax of our
state machines to be able to deal with booleans and products (the details can be
found
[here](https://github.com/stevana/hot-swapping-state-machines2/blob/main/src/Interpreter.hs)).
```haskell
counterV3 :: T (Int, Bool) String String
counterV3 = Read >>> counterV3' >>> Show
where
counterV3' :: T (Int, Bool) InputV3 OutputV3
counterV3' =
-- Toggle negates the boolean in the state (the second component).
(Get >>> Second Not >>> Put) `Case`
-- Reset resets the counter and the boolean back to false (i.e. incrementing).
(Int 0 :&&& Bool False >>> Put) `Case`
-- Reading the counter picks out the first component from the state.
(Get >>> Fst) `Case`
-- Incrementing or decrementing, depending on the boolean in the state.
(Get >>> If Decr Incr >>> (Id :&&& (Consume >>> Get >>> Snd)) >>> Put)
```
We can then upgrade to our new version of the counter as follows.
```haskell
let msg2 :: Msg ()
msg2 = Upgrade Nothing "counter"
(UpgradeData_ UTInt (UTPair UTInt UTBool) UTString UTString
(erase counterV3) (erase (Id :&&& Bool False)))
nc "127.0.0.1" 3000 msg2
```
Notice how the state is migrated using `Id :&&& Bool False`, i.e. create a pair
where the first component is the old value of the state (this is the current
count) and the second component is `False` (this is whether we are decrementing).
Here's a final example of how we can use the new counter.
```haskell
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show ToggleCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))
```
The above yields the following output.
```
UpgradeSucceeded "counter"
Item "Right (Right (Left 0))" -- The counter is 0.
Item "Right (Right (Right ()))" -- Two increments.
Item "Right (Right (Right ()))"
Item "Right (Right (Left 2))" -- The counter is 2.
Item "Left ()" -- Toggle to decrementing.
Item "Right (Right (Right ()))" -- Decrement.
Item "Right (Right (Left 1))" -- The value is 1.
```
## Discussion and future work
If we look back at the list, from the introduction, of properties that we wanted
from our upgrades, then I hope that I've managed to provide a glimpse of a
possible way of achieving zero-downtime upgrades with type-safe state migrations
that are atomic.
Downgrades can be thought of as an upgrade to an earlier version, although it
could be interesting to experiment with requiring an inverse function to the
state migration as part of an upgrade. That way the system itself could
downgrade in case there's more than N errors within some time period, or
something like that.
I didn't talk about backwards and forwards compatibility. We could probably use
an [interface description
language](https://en.wikipedia.org/wiki/Interface_description_language), such as
Avro or Protobuf, but it could also be interesting see if we could add input and
output migrations as part of upgrades (in addition to state migrations).
Especially in conjunction with being able to derive them generically and
[automatically](https://www.manuelbaerenz.de/essence-of-live-coding/EssenceOfLiveCoding.pdf)
from the schema change.
There's also a bunch of other
[things](https://github.com/stevana/hot-swapping-state-machines2/blob/main/TODO.md)
that I thought of while working on this, which I don't have any good answers for
yet. If you feel that I'm missing something, or if you know some answers or if
any of these problems sound interesting to work on, please do feel free to get
in [touch](https://stevana.github.io/about.html)!
Let me close by trying to tie it back to Barbara Liskov's remark about the need
for more complete programming languages. In a world where software systems are
expected to evolve over time, wouldn't it be neat if programming languages
provided some notion of upgrade and could typecheck our code *across versions*,
as opposed to merely typechecking a version of the code in isolation from the
next?
[^1]: State machines might seem like low-level clumsy way of programming, but
Yuri Gurevich has
[shown](https://www.microsoft.com/en-us/research/publication/103-evolving-algebras-1993-lipari-guide/)
that abstract state machines (state machines where state can be any
first-order structure) can avoid the Turing tarpit and capture any algorithm
at any level of abstraction. This result is a generalisation of the
Church-Turing thesis from computable functions on natural numbers to
arbitrary sequential algorithms.
In case you're not convinced by this theoretical argument, then here are a
couple of practical examples of state machine use from industry.
In Joe Armstrong's PhD
[thesis](http://kth.diva-portal.org/smash/record.jsf?pid=diva2%3A9492&dswid=-4551)
(2003), Joe gives an example of a big Ericsson telecommunications system
built in Erlang/OTP using a handful of library constructs (behaviours). The
most commonly used of these building blocks is `gen_server`, which is a
state machine. I've written a high-level summary of the ideas over
[here](https://stevana.github.io/erlangs_not_about_lightweight_processes_and_message_passing.html),
although I recommend reading his thesis and forming your own conclusions.
Leslie Lamport is another proponent of state machines. His TLA+ is basically
a language for describing state machines. See his article [*Computation and
State
Machines*](https://www.microsoft.com/en-us/research/publication/computation-state-machines/)
(2008) for an introduction. Fault tolerance in distributed systems is often
realised by means of replicated state machines, which Leslie helped develop
back in the 80s.
Jean-Raymond Abrial's B-method (a successor to Z notation) is also centered
around state machines and has been used to verify the automatic Paris Métro
lines 14 and 1 and the Ariane 5 rocket.
[^2]: Many years ago I had the pleasure to study interaction structures (aka
index containers aka polynomial functors). One of many possible way to view
these structures is as if they are state machines. One can construct a
category with the objects being interaction structures and then think about
what the morphisms must look like in order to satisfy the necessary
categorical laws.
I don't know much about category theory myself, but I remember that the
morphisms in the resulting category have two components and they look
exactly like those that we needed to be able to support backwards
compatibility.
There's also a strong [connection](https://arxiv.org/abs/0905.4063v1)
between this category and stepwise refinement or refinement calculus, which
at least intuitively has some connection with upgrades.
I suppose that there are more useful ideas to steal from there.
[^3]: This restriction makes it easier to make everything deterministic, which
in turn makes it easier to (simulation) test. I touch upon this in an
earlier
[post](https://stevana.github.io/erlangs_not_about_lightweight_processes_and_message_passing.html)
towards the end. I hope to expand upon this in a separate post at some point
in the future.
It also make it possible for the implementation to be more efficient. For
example, if we want to have a pipeline that takes the output of one state
machine and broadcasts it to two other state machines (on the same computer)
then in Erlang the output would be copied to the two state machines
downstream, whereas with pipelines we can do it [without
copying](https://stevana.github.io/parallel_stream_processing_with_zero-copy_fan-out_and_sharding.html).
[^4]: People familiar with Haskell's ecosystem might recognise that this is an
instance of
[`Category`](https://hackage.haskell.org/package/base-4.19.1.0/docs/Control-Category.html)
and partially an instance of
[`Cocartesian`](https://github.com/stevana/hot-swapping-state-machines2/blob/main/src/Classes.hs#L13),
plus some extras. In a "real" implementation we would want this datatype to
be an instance of `Cocartesian` instance as well as `Cartesian`.