Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/stla/scubature
Integration over simplices.
https://github.com/stla/scubature
haskell integration
Last synced: 3 months ago
JSON representation
Integration over simplices.
- Host: GitHub
- URL: https://github.com/stla/scubature
- Owner: stla
- License: gpl-3.0
- Created: 2022-07-22T18:27:20.000Z (over 2 years ago)
- Default Branch: main
- Last Pushed: 2022-12-12T09:54:26.000Z (about 2 years ago)
- Last Synced: 2024-09-29T17:41:58.578Z (4 months ago)
- Topics: haskell, integration
- Language: Haskell
- Homepage:
- Size: 47.9 KB
- Stars: 3
- Watchers: 2
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- Changelog: CHANGELOG.md
- License: LICENSE
Awesome Lists containing this project
README
# scubature
Pure Haskell implementation of simplicial cubature (integration over a simplex).
This library is a port of a part of the R package **SimplicalCubature**,
written by John P. Nolan, and which contains R translations of
some Matlab and Fortran code written by Alan Genz.
It is also a port of a part of the R package **SphericalCubature**, also
written by John P. Nolan.
In addition it provides a function for the exact computation of the integral
of a polynomial over a simplex.
___
## Integral of a function on a simplex
```haskell
integrateOnSimplex
:: (VectorD -> VectorD) -- integrand
-> Simplices -- domain of integration (union of the simplices)
-> Int -- number of components of the integrand
-> Int -- maximum number of evaluations
-> Double -- desired absolute error
-> Double -- desired relative error
-> Int -- integration rule: 1, 2, 3 or 4
-> IO Results -- values, error estimates, evaluations, success
```
### Example
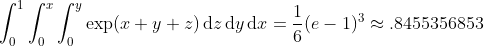
Define the integrand:
```haskell
import Data.Vector.Unboxed as V
:{
f :: Vector Double -> Vector Double
f v = singleton $ exp (V.sum v)
:}
```
Define the simplex (tetrahedron in dimension 3) by the list of its vertices:
```haskell
simplex = [[0, 0, 0], [1, 1, 1], [0, 1, 1], [0, 0, 1]]
```
Integrate:
```haskell
import Numeric.Integration.SimplexCubature
integrateOnSimplex f [simplex] 1 100000 0 1e-10 3
-- Results { values = [0.8455356852954488]
-- , errorEstimates = [8.082378899762402e-11]
-- , evaluations = 8700
-- , success = True }
```
For a scalar-valued integrand, it's more convenient to define... a scalar-valued
integrand! That is:
```haskell
:{
f :: Vector Double -> Double
f v = exp (V.sum v)
:}
```
and then to use `integrateOnSimplex'`:
```haskell
integrateOnSimplex' f [simplex] 100000 0 1e-10 3
-- Result { value = 0.8455356852954488
-- , errorEstimate = 8.082378899762402e-11
-- , evaluations = 8700
-- , success = True }
```
## Exact integral of a polynomial on a simplex
```haskell
integratePolynomialOnSimplex
:: (C a, Fractional a, Ord a) -- `C a` means that `a` must be a ring
=> Spray a -- ^ polynomial to be integrated
-> [[a]] -- ^ simplex to integrate over
-> a
```
### Example
We take as an example the rational numbers for `a`. Thus we must take a
polynomial with rational coefficients and a simplex whose vertices
have rational coordinates. Then the integral will be a rational number.
Our polynomial is
&space;=&space;x^4&space;+&space;y&space;+&space;2xy^2&space;-&space;3z.)
It must be defined in Haskell with the
[**hspray**](https://github.com/stla/hspray) library.
```haskell
import Numeric.Integration.IntegratePolynomialOnSimplex
import Data.Ratio
import Math.Algebra.Hspray
:{
simplex :: [[Rational]]
simplex = [[1, 1, 1], [2, 2, 3], [3, 4, 5], [3, 2, 1]]
:}
x = lone 1 :: Spray Rational
y = lone 2 :: Spray Rational
z = lone 3 :: Spray Rational
:{
poly :: Spray Rational
poly = x^**^4 ^+^ y ^+^ 2.^(x ^*^ y^**^2) ^-^ 3.^z
:}
integratePolynomialOnSimplex poly simplex
-- 1387 % 42
```
## Integration on a spherical triangle
The library also allows to evaluate an integral on a spherical simplex on the
unit sphere (in dimension 3, a spherical triangle).
### Example
For example take the first orthant in dimension 3:
```haskell
import Numeric.Integration.SphericalSimplexCubature
o1 = orthants 3 !! 0
o1
-- [ [1.0, 0.0, 0.0]
-- , [0.0, 1.0, 0.0]
-- , [0.0, 0.0, 1.0] ]
```
And this integrand:
```haskell
:{
integrand :: [Double] -> Double
integrand x = (x!!0 * x!!0 * x!!2) + (x!!1 * x!!1 * x!!2) + (x!!2 * x!!2 * x!!2)
:}
```
Compute the integral (the exact result is `pi/4 ≈ 0.7853981634`):
```haskell
integrateOnSphericalSimplex integrand o1 20000 0 1e-7 3
-- Result { value = 0.7853981641913279
-- , errorEstimate = 7.71579524444753e-8
-- , evaluations = 17065
-- , success = True }
```
## References
- A. Genz and R. Cools.
*An adaptive numerical cubature algorithm for simplices.*
ACM Trans. Math. Software 29, 297-308 (2003).
- Jean B. Lasserre.
*Simple formula for the integration of polynomials on a simplex.*
BIT Numerical Mathematics 61, 523-533 (2021).