https://github.com/stla/simplicialcubature
Multidimensional integration on simplices.
https://github.com/stla/simplicialcubature
haskell
Last synced: 7 months ago
JSON representation
Multidimensional integration on simplices.
- Host: GitHub
- URL: https://github.com/stla/simplicialcubature
- Owner: stla
- Created: 2017-12-28T00:05:59.000Z (about 8 years ago)
- Default Branch: master
- Last Pushed: 2018-02-13T00:19:36.000Z (almost 8 years ago)
- Last Synced: 2025-02-06T16:05:47.162Z (12 months ago)
- Topics: haskell
- Language: Haskell
- Homepage:
- Size: 90.8 KB
- Stars: 1
- Watchers: 3
- Forks: 1
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# simplicialcubature
Pure Haskell implementation of simplicial cubature (integration on a simplex).
```haskell
integrateOnSimplex
:: (VectorD -> VectorD) -- integrand
-> Simplices -- domain of integration (union of the simplices)
-> Int -- number of components of the integrand
-> Int -- maximum number of evaluations
-> Double -- desired absolute error
-> Double -- desired relative error
-> Int -- integration rule: 1, 2, 3 or 4
-> IO Results -- values, error estimates, evaluations, success
```
## Example
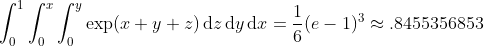
Define the integrand:
```haskell
import Data.Vector.Unboxed as V
f :: Vector Double -> Vector Double
f v = singleton $ exp (V.sum v)
```
Define the simplex:
```haskell
simplex = [[0,0,0],[1,1,1],[0,1,1],[0,0,1]]
```
Integrate:
```haskell
> import SimplexCubature
> integrateOnSimplex f [simplex] 1 100000 0 1e-10 3
Results { values = [0.8455356852954488]
, errorEstimates = [8.082378899762402e-11]
, evaluations = 8700
, success = True }
```
For a scalar-valued integrand, it's more convenient to define... a scalar-valued
integrand! That is:
```haskell
f :: Vector Double -> Double
f v = exp (V.sum v)
```
and then to use `integrateOnSimplex'`:
```haskell
> integrateOnSimplex' f [simplex] 100000 0 1e-10 3
Result { value = 0.8455356852954488
, errorEstimate = 8.082378899762402e-11
, evaluations = 8700
, success = True }
```
## Integration on a spherical triangle
The library also allows to evaluate an integral on a spherical simplex on the
unit sphere (in dimension 3, a spherical triangle).
For example take the first orthant in dimension 3:
```haskell
> import SphericalSimplexCubature
> o1 = orthants 3 !! 0
> o1
[ [1.0, 0.0, 0.0]
, [0.0, 1.0, 0.0]
, [0.0, 0.0, 1.0] ]
```
And this integrand:
```haskell
integrand :: [Double] -> Double
integrand x = x!!0 * x!!0 * x!!2 + x!!1 * x!!1 * x!!2 + x!!2 * x!!2 * x!!2
```
Compute the integral (the exact result is `pi/4`):
```haskell
> integrateOnSphericalSimplex integrand o1 10000 0 1e-5 3
Result { value = 0.7853978756312796
, errorEstimate = 7.248620366022506e-6
, evaluations = 3282
, success = True }
```