Data

Tools

Indexes

Applications

Experiments

Awesome

An open API service indexing awesome lists of open source software.

https://github.com/szymon423/tsp-cpu-vs-gpu

Simple brute force approach to solve travelling salesman problem with CPU and GPU
https://github.com/szymon423/tsp-cpu-vs-gpu

cuda tsp

Last synced: 7 months ago
JSON representation

Simple brute force approach to solve travelling salesman problem with CPU and GPU

Awesome Lists containing this project

README 

          
# Travelling salesman problem CPU vs GPU



Rozpoczynając ten projekt przyjąłem podejście, w którym chciałbym wyznaczyć wszystkie możliwe permutacje dla danych n węzów, które reprezentują n miast, które nasz komiwojażer miałby odwiedzić. Ze względu na to, że istotny jest punkt startu, to sztucznie dokładając pierwsze miasto oraz obliczając n! możliwości uzyskujemy łącznie rozwiązania problemu dla n+1 miast, gdzie n! to liczba rozwiązań.



## Znaleziony kod

Na ten moment mam znaleziony działający algorytm, który oblicza wszystkie możliwe permutacje maksymalnie dla 12 węzłów. Dodając stały początkowy węzeł otrzymujemy rozwiązanie TSP dla 13 miast. Jednak nie do końca rozumiem jak działa to co gość, od którego mam kod zrobił. 



Link do znalezionego kodu, który liczy do max 12!



## Moje podejście

Staram się też jednak samemu napisać od podstaw taki algorytm, który zadziała na CUDA. W tym jednak pojawia się problem, bo mając klasyczne algorytmy wyznaczające wszystkie permutacje trochę ciężko wyznaczyć drogę, która pozwoli na zrównoleglenie obliczeń - a w zasadzie ja tego nie potafię zrobić. Rekurencja jest trudna w zrównolegleniu więc też odpada. Z tego powodu odrzuciłem kilka algorytmów:

 * prosty algorytm z rekurencją - zagnieżdżone n pętli

 * algorytm Heaps'a oraz QuickPerm są efektywne, jednak podczas działania nie widzę możliwości sensownego zrównoleglenia - nie zwracają wyników w leksykograficznej kolejności



Właśnie dwa ostatnie słowa to według mnie klucz do obliczeń równoległych.



## Kolejność leksykograficzna

Jeśli będziemy generować wszystkie możliwe permutacje w takiej właśnie kolejności zaczynając od najmniejszej oraz najbardziej intuicyjnej permutacji początkowej, którą będzie {1, 2, 3, ..., n}, wówczas mamy pewność, że wygenerujemy wszystkie możliwe permutacje realizując je po kolei aż do ostatniej, którą jest inwersją permutacji początkowej: {n, n-1, n-2, ..., 1}.



### Wszystko fajnie, tylko jak generować permutacje w kolejności leksykograficznej?



Ważne jest to, że leksykograficznie w naszym przypadku oznacza po prostu rosnąco, czyli tak jakbyśmy posortowali wyniki dla jakiegoś algorytmu, tak żeby liczba tworząca następną permutację była najmniejszą z wszystkich możliwych następnych permutacji. Przykład dla 3 elementów, 3! = 6. 




  

    i arr[0] arr[1] arr[2]

  

   1 1 2 3 

   2 1 3 2 

   3 2 1 3 

   4 2 3 1 

   5 3 1 2 

   6 3 2 1 






Znalazłem gościa, który bardzo fajnie wyjaśnił o co biega na tym filmiku na YT ale postaram się wyjaśnić to też tutaj.



### Wyznaczanie następnej permutacji w kolejności leksykograficznej

  

Wyznaczmy następną permutację dla n = 7 elementowej tablicy: {3, 2, 6, 7, 5, 4, 1}.

Indeksując kazdy element od 0 do n-1, możemy przedstawić tę tablicę za pomocą prostego wykresu:



    




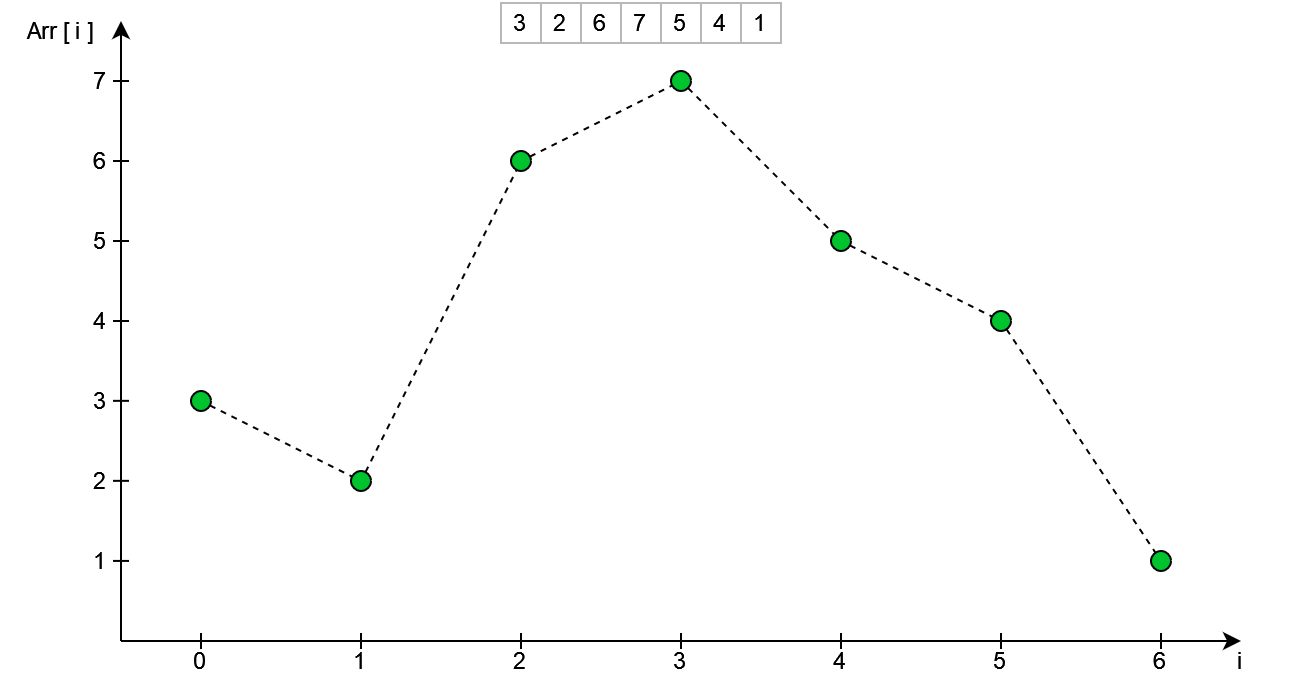
Następnym krokiem jest znalezienie wierzchołka - patrząc z prawej strony. W kodzie wykonane zostanie to przez iterowanie się od końca tablicy do początku - sprawdzając przy tym czy aktualny element jest mniejszy od poprzedniego.



    




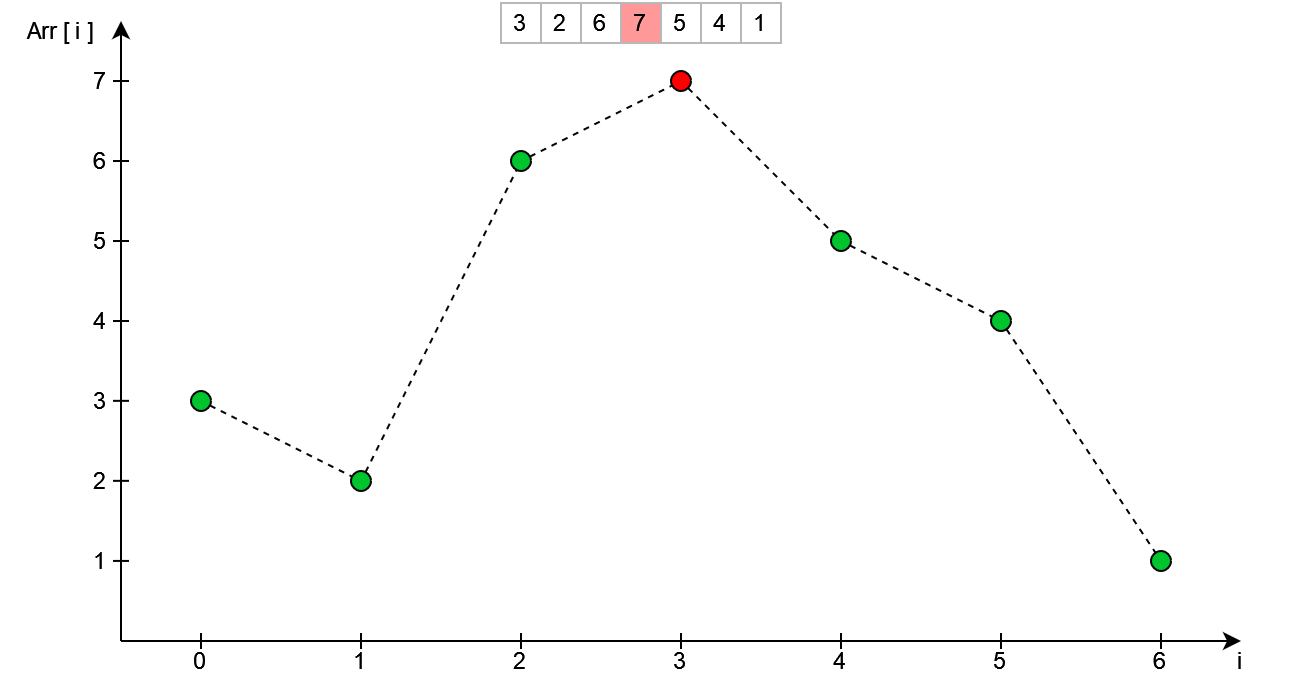
W tym przypadku jest to element o indeksie i = 3, został oznaczony na czerwono. W celu wyznaczenia kolejnej permutacji musimy zamienić miejscami wyznaczony właśnie element z poprzednim (o indeksie i - 1 = 2). Uzyskana wówczas tablica jest następująca:



    




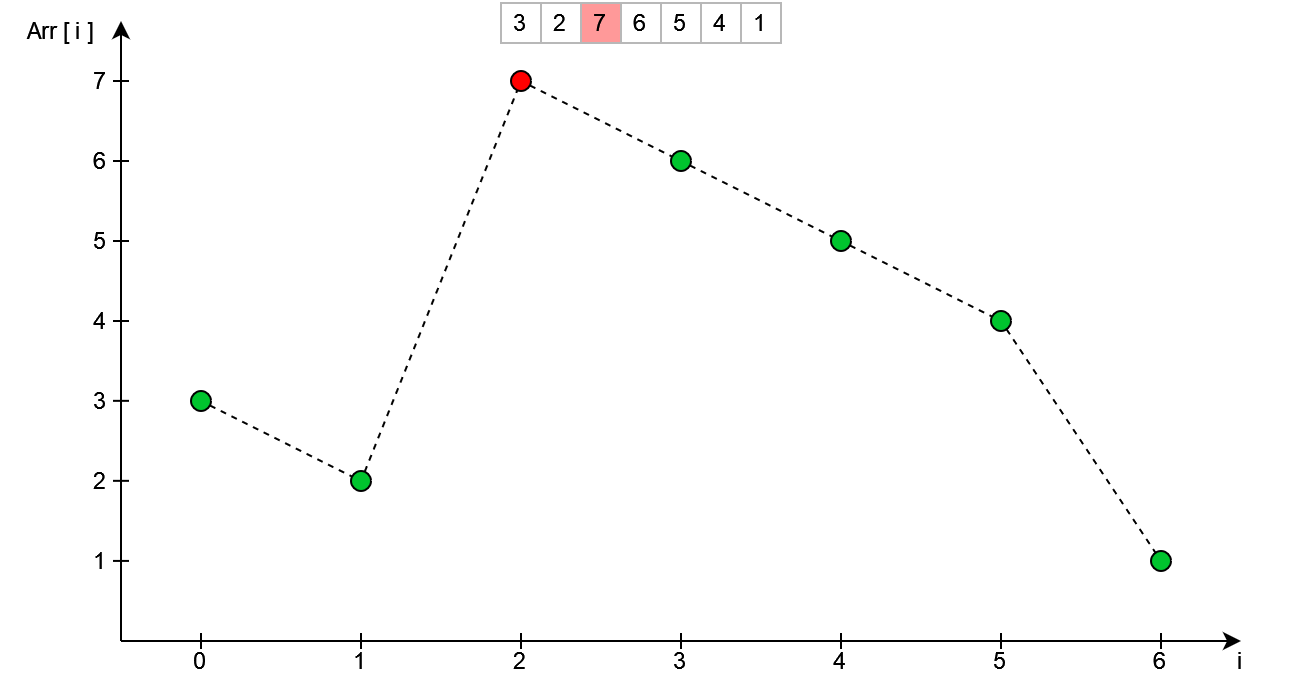
Nie jest to jednak ostateczny układ liczb, oznaczający końcową permutację. Aby ją uzyskać musimy posortować rosnąco wszystkie elementy znajdujące się na prawo od nowego miejsca w którym znajduje się wierzchołek (bez niego samego). Zostało to przedstawione poniżej - wierzchołki oznaczone na niebiesko.



    




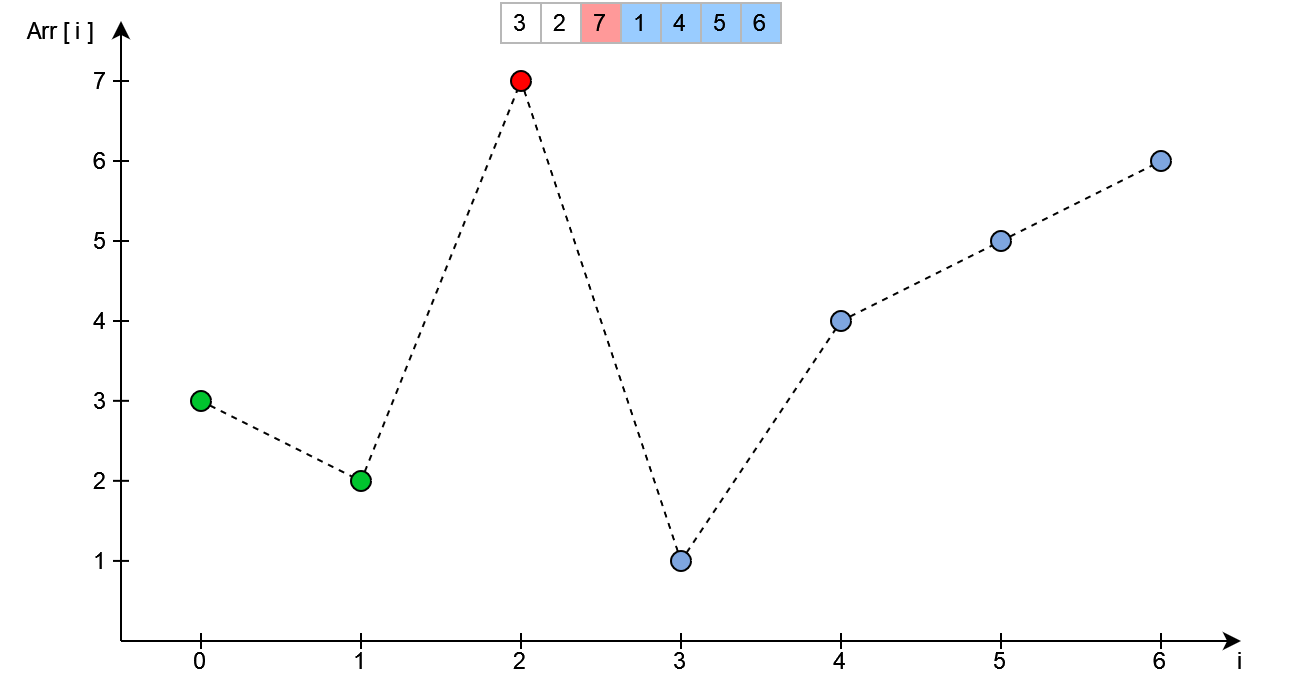
Uzyskana w ten sposób tablica będzie najmniejszą z wszystkich możliwych kolejnych permutacji tablicy początkowej. Należy jednak dodatkowo rozpatrzyć jeden przypadek, w którym algorytm działa inaczej - pokazano go na poniższej tablicy.



    

  

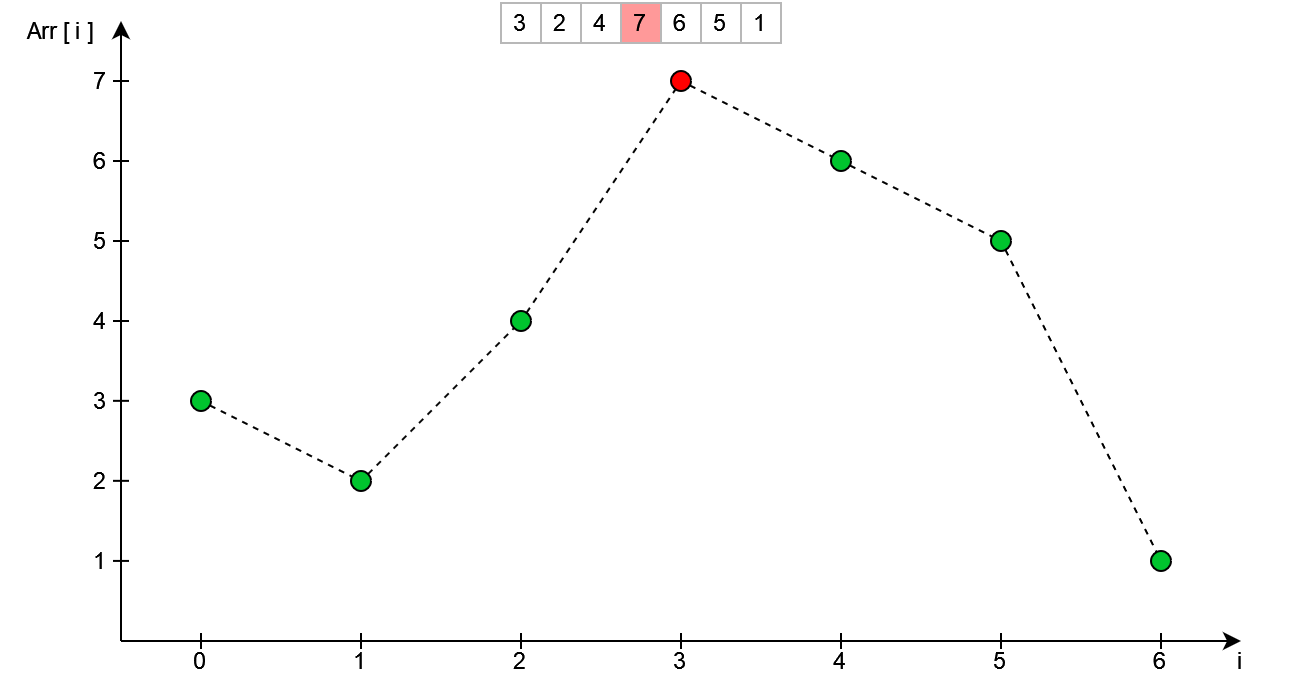
Jak widać na powyższym rysunku, znaleziony został pierwszy wierzchołek (maksimum lokalne) oraz znajduje się on pod indeksem i = 3. Zamieniając kolejnością elementy i = 3 oraz i = 2, oraz sortując elementy dla i > 2, nie uzyskalibyśmy kolejnej permutacji w kolejności leksykograficznej. 

  

Jest to spowodowane przez fakt, że na prawo od wierzchołka znajdują się liczby, które są mniejsze od samego wierzchołka i są również większe od elementu o indeksie i = 2. W takim przypadku należy wybrać najmniejszy z elementów znajdujących się na prawo od miejsca w którym chcemy dokonać zmian (indeks i = 2). W tym przypadku najmniejszy z dostępnych elementów znajduje się pod indeksem i = 5. Tak więc następuje zamiana elementów o indeksach i = 2 oraz i = 5 tak jak pokazano na poniższym rysunku.



    

  

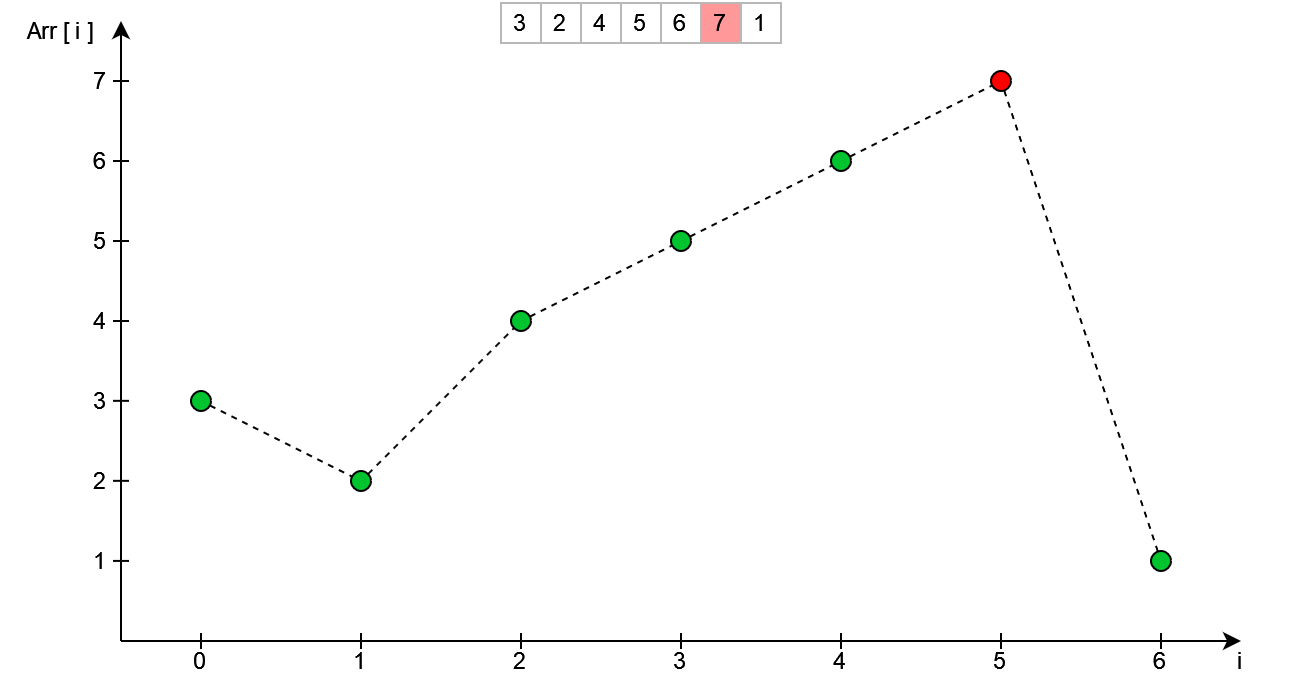
Kolejnym krokiem tak jak poprzednio jest posortowanie poszczególnych elementów - w tym przypadku dla indeksów i > 2. Zostało to przedstawione poniżej.



    



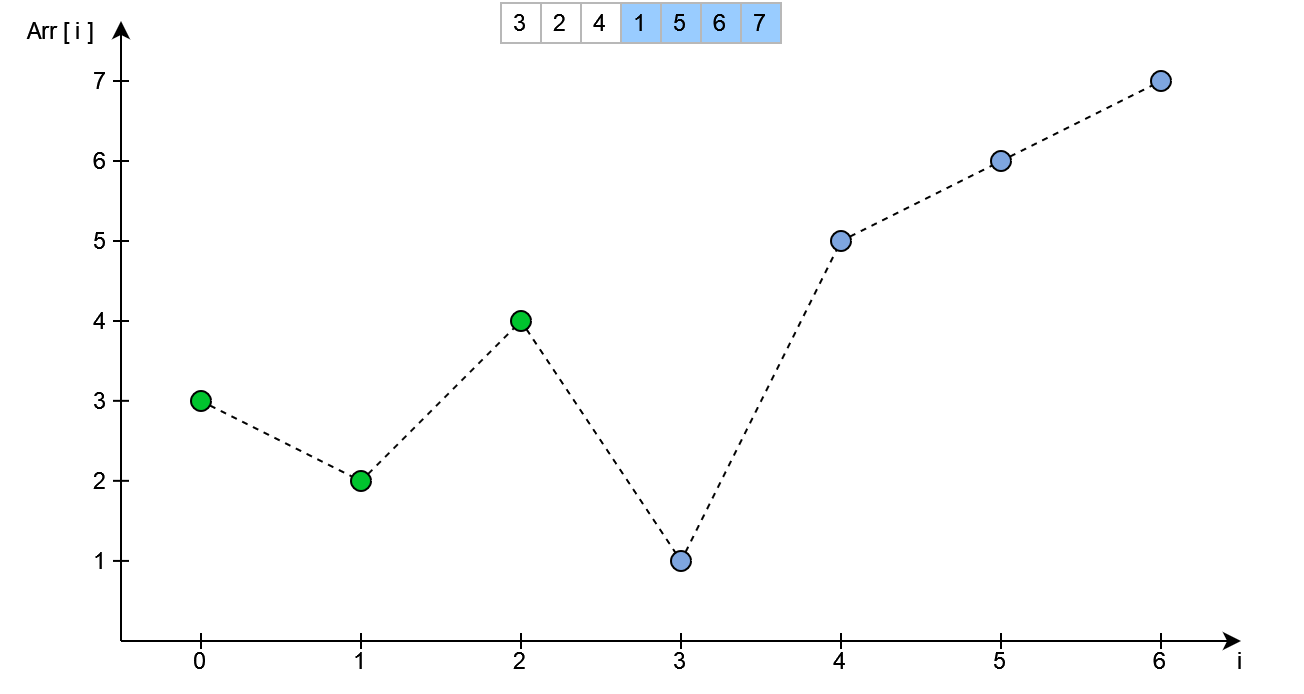
W ten sposób możemy uzyskać kolejną permutację dla dowolnego przypadku - ograniczeniem jest brak możliwości występowania elementów o jednakowej wartości pod różnymi adresami. W TSP jednak nie występuje taka zależność.

  

## Wyznaczanie i-tej permutacji

Aby móc równolegle obliczać kolejne permutacje potrzebujemy znać zbiór permutacji początkowych, od których poszczególne wątki będą przeprowadzać obliczenia związane z wyznaczeniem kolejnych permutacji.



    



Powyższa grafika przedstawia przestrzeń do wyznaczenia wszystkich iteracji dla zbioru składającego się z 4 elementów. Wszystkich permutacji jest 4! = 24. Chcąc realizować te peramutacje równolegle korzystając z uprzednio przedstawionego algorytmu musimy poznać pierwszą permutację dla każdego podzbioru permutacji - zostały one rozróżnione kolorami. Elementy o indeksach i = 0, 6, 12, 18 są pierwszymi w każdym podzbiorze. Musimy więc wyznaczyć permutacje początkowe dla tych elementów.

  

Korzystając z tego, że wyznaczamy permutacje w kolejności leksykograficznej możemy obliczać jaka będzie i-ta permutacja za pomocą sprytnego algorytmu opartego na silniowym systemie pozycyjnym (Factorial number system)

  

### Factorial number system

Zeby zrozumieć o co chodzi chcę przywołać analogię do systemu dziesiętnego. W systemie dziesiętnym liczby zapisywane są za pomocą ciągu cyfr, gdzie docelowa wartość liczby stworzonej przez ten ciąg jest liczona na bazie dziesiętnej:



    




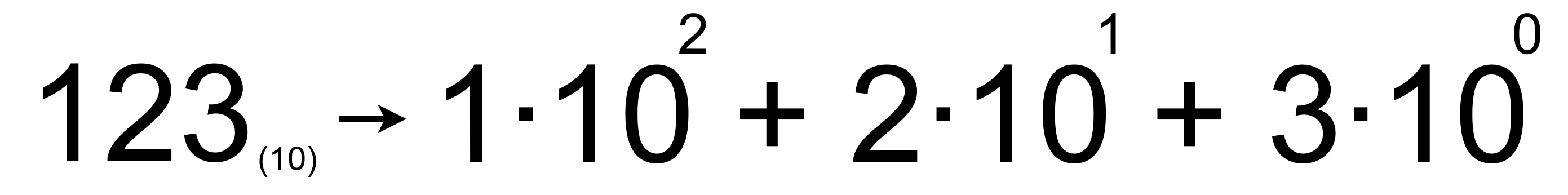
W przypadku systemu silniowego bazą zapisu jest silnia. Liczbę z systemu dziesiętnego możemy przenieść do systemu silniowego realizując operację rozkładu za pomocą dzielenia z resztą. Dla przykładu rozważmy znów 123:






   Dzielna Dzielnik Reszta z dzielenia 

   123 1 0

   123 2 1 

   61 3 1 

   20 4 0

   5 5 0 

   1 6 1 



  



Wykonane operacje:

  

1. W pierwszym kroku dzielimy liczbę 123 przez 1, efektem tego jest liczba 123 oraz 0 reszty,

2. Następnie dzielimy wyżej uzyskany rezultat przez kolejną liczbę jaką jest 2 - uzyskujemy 61 całości oraz 1 reszty,

3. Liczbę 61 dzielimy przez kolejny dzielnik jakim jest 3 co daje 20 całości i 1 reszty,

4. Liczbę 20 dzielimy przez 4 co daje 5 całości i 0 reszty,

5. Liczbę 5 dzielimy przez 5 co daje 1 całości i 0 reszty,

6. Liczbę 1 dzielimy przez 6 co daje 0 całości i 1 reszty.

  

W powyższym zestawie operacji istotny jest zapis reszty. Reprezentacją liczby 123 (system dziesiętny) w systemie silniowym jest ciąg 1:0:0:1:1:0!

  

### Co to ma wspólnego z i-tą permutacją?

  

To jest ciekawe ponieważ, chcąc wyznaczyć i-tą permutację na zbiorze n elementów ułożonych w kolejności leksykograficznej w początkowej permutacji np: dla n = 4   :   1, 2, 3, 4 możemy obliczyć reprezentację silniową liczby która określa numer permutacji, który chcemy uzyskać. Obliczmy np 4 permutację na powyższym zbiorze. 



Na początek zrobimy to ręcznie:

  




   Zbiór początkowy 1 2 3 4 

   Permutacja 1 1 2 4 3 

   Permutacja 2 1 3 2 4 

   Permutacja 3 1 3 4 3 

   Permutacja 4 1 4 2 3 






Zapiszmy teraz numer permutacji którą chcemy uzyskać w reprezentacji silniowej.




   Dzielna Dzielnik Reszta z dzielenia 

   4 1 0

   4 2 0 

   3 3 2 



  

 

Wiemy teraz, że reprezentacja silniowa liczby 4 wynosi:




   2 0 0 





  

Ten ciąg liczb jest bardzo ważny. Musimy jednak go zmodyfikować ponieważ każda z cyfr w tym ciągu odnosi się do cyfry w permutacji początkowej, w której mamy 4 cyfry, tak więc, żeby nasz ciąg miał 4 cyfry, dopisujemy z jego lewej strony zera, tak by dopełnić do odpowiedniej liczby cyfr. Tak więc docelowy ciąg będzie w postaci:




   0 2 0 0 






Na tej podstawie możemy obliczyć jakie elementy należy poddać permutacji. Zabawa polega na tym, że iterujemy się przez poszczególne cyfry powyższego ciągu od lewej do prawej. Każda kolejna cyfra oznacza jaką liczbę ze zbioru cyfr wchodzących w skład permutacji początkowej ułożonej leksykograficznie:




   liczba 1 2 3 4 

   indeks 0 1 2 3 






Pierwsza liczba w ciągu silniowym to 0, oznacza to, że jako pierwszą cyfrę do docelowej permutacji należy wybrać element na zerowej pozycji z początkowego zbioru liczb. Będzie to 1. Następnie ze zbioru dostępnych elementów usuwamy jedynkę oraz aktualizujemy indeksy. Kolejna cyfra to 2. Oznacza to, że na drugiej pozycji w docelowej permutacji znajdzie się liczba o indeksie 2 ze zbioru dostępnych elementów - jest nią 4. Realizujemy ten algorytm dla pozostałych elementów, tak jak pokazano na poniższym rysunku:



    




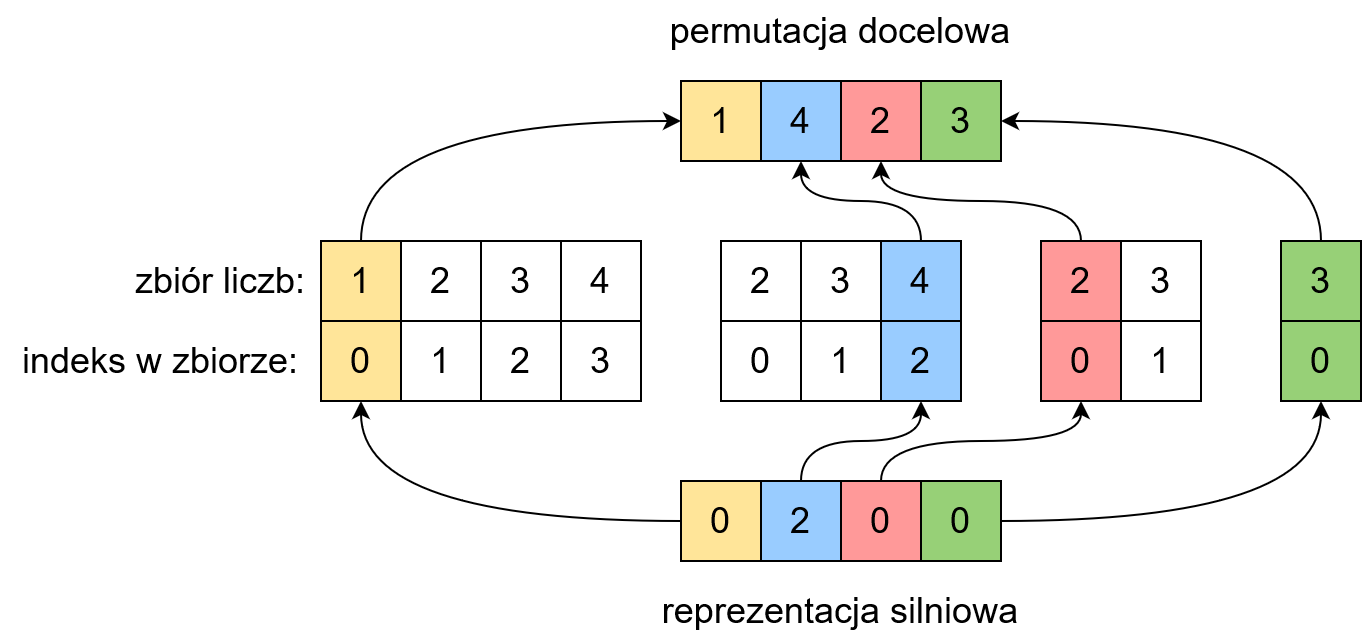
Jak widać, uzyskana permutacja jest dokładnie taka sama jak ręcznie wyznaczona wcześniej.

  

# Obliczenia równoległe



Podejście jakie planuję przyjąć jest dwojakie:

 * każdy i-ty wątek liczy i-tą permutację. 

 * każdy z wątków oblicza kolejne permutacje dla swojej grupy, która definiowana jest przez permutację początkową wyliczoną na podstawie rozkładu silniowego



## i-ty wątek liczy i-tą permutację



Problemem w tym podejściu jest fakt, że nie mamy nieskończoność wątków, tylko 1024 * 1024 * 64 = 67 108 864. Oznacza to, że jednorazowo będziemy mogli obliczyć nawet 11! permutacji, ponieważ 11! = 39 916 800. Chcąc obliczyć pozostałe permutacje, będziemy musieli wszystkie wątki ponownie zaprzęc do roboty, tak, żeby obliczyły pozostałe permutacje gdy ich łączna ilość przekracza ~67 milionów.



### Uzyskane rezultaty

Niestety efekty obliczeń nie są satysfakcjonujące. GPU jest przy aktualnym algorytmie wolniejsze od CPU...

Tak prezentują się czasy obliczeń dla poszczególnej liczby węzłów:





    

    




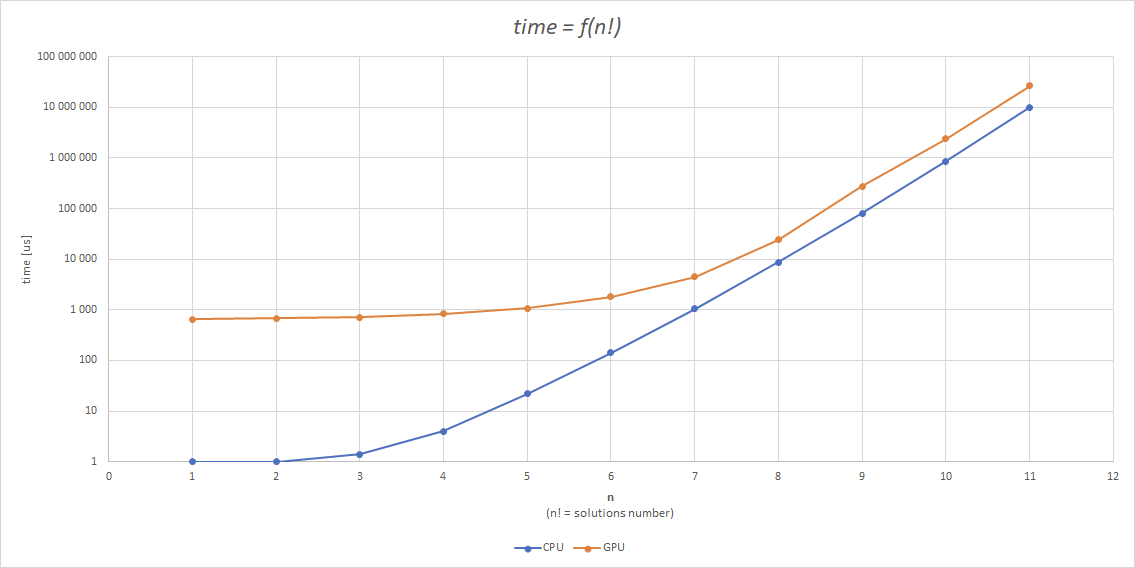
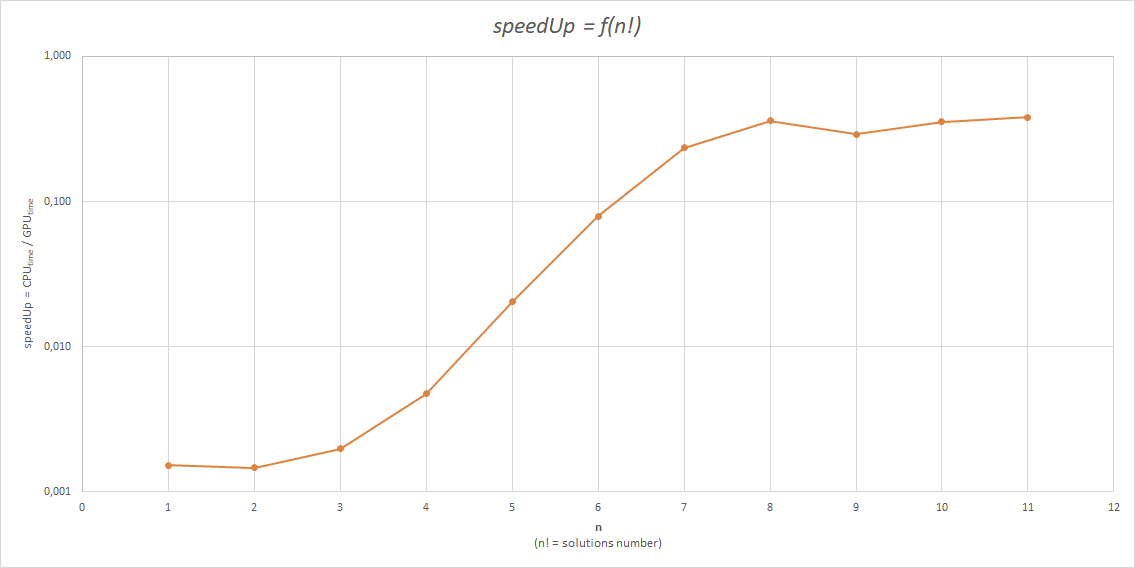
Jak widać, tego typu podejście nie jest wydajne oraz w zasadzie zrównoleglenie tego procesu w tem sposób powoduje jego spowolnienie.



## i-ty wątek wyznacza grupę permutacji rozpoczynając od k-tej permutacji



W tym przypadku za pomocą jednej grupy wątków, możemy obliczyć wszystkie permutacje "jednocześnie". Algorytm składa się z czterech kroków:

* wyznaczenie pierwszej permutacji dla danego wątka za pomocą rozkładu silniowego,

* wyznaczenie wszystkich pozostałych permutacji w kolejności leksykograficznej jakie ma wygenerować ten wątek,

* lokalne wyznaczenie permutacji o minimalnej funkcji celu (długości),

* globalne wyznaczenie minimum pośrud minimów lokalnych.





    

    




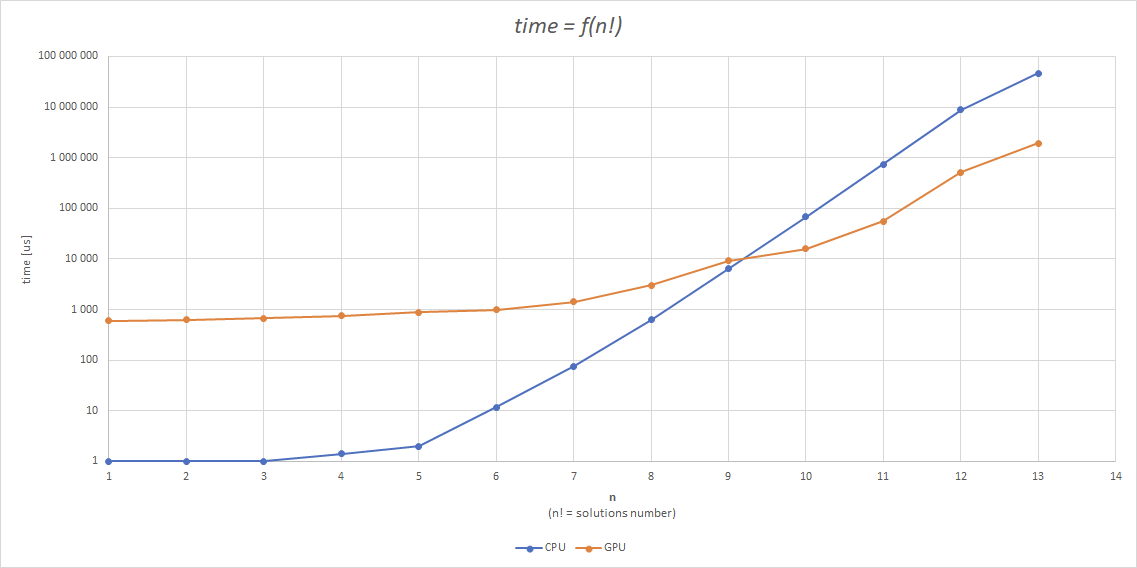
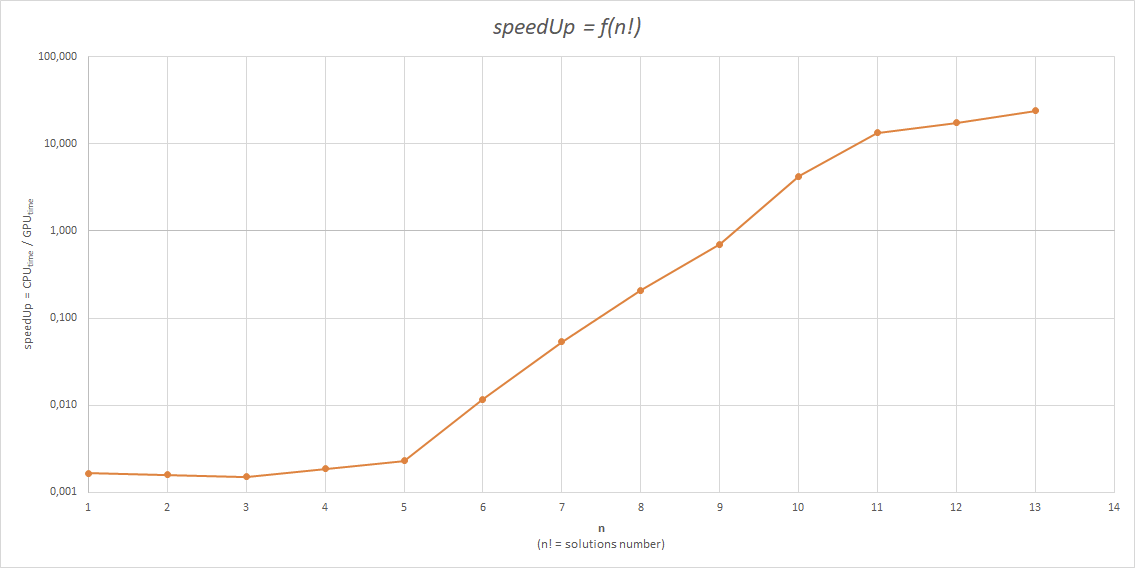
Jak widać w tym przypadku rezultaty są dużo lepsze. W najlepszym przypadku uzyskane przyspieszenie obliczeń skraca ich czas 24 krotnie.  



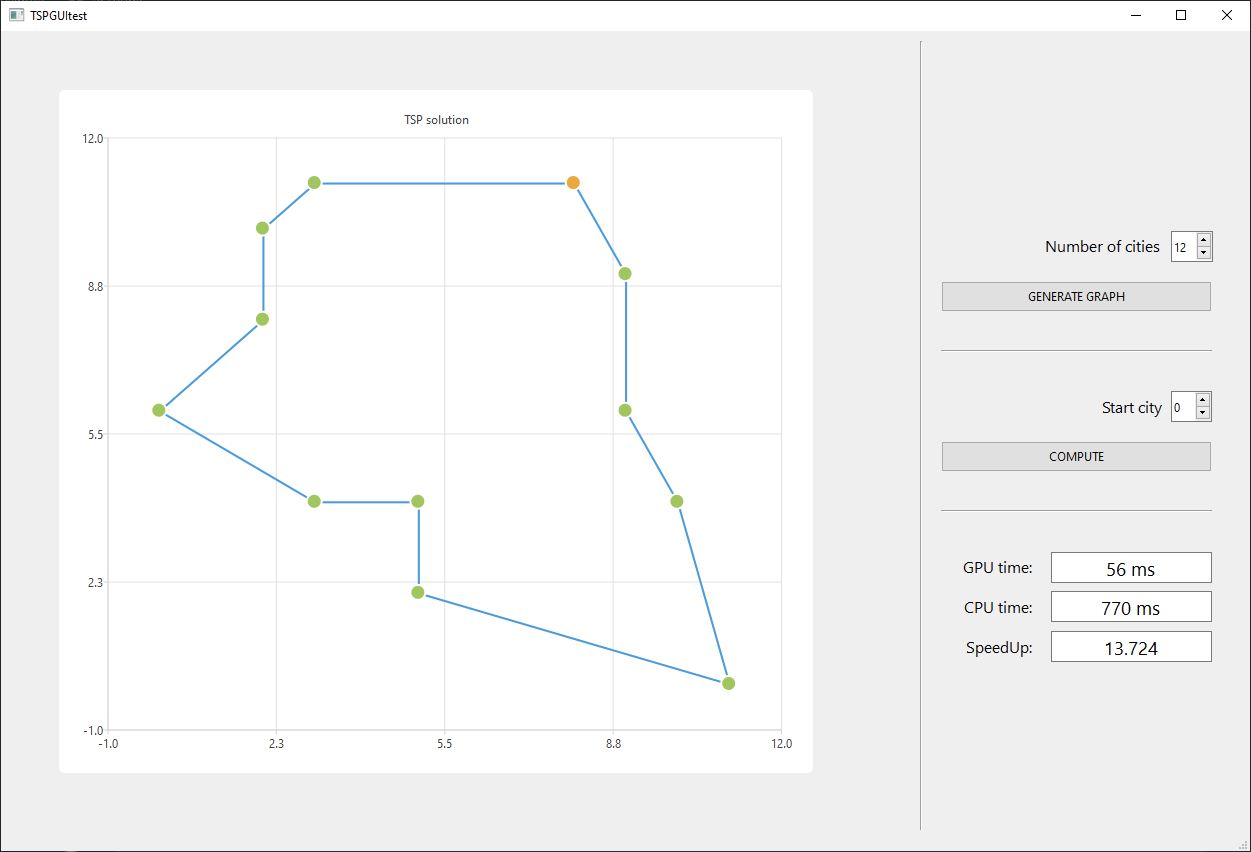
## Dorzucone zostało GUI do wygodnego testowania, nie jest jeszcze idealne, ale spełnia swoją rolę





    



  

Jak widać powyżej, możemy wybrać liczbę miast do odwiedzenia (m), oraz na tej podstawie wylosować mapę miast. Położenie konkretnego punktu na mapie jest wybierane jako punkt o współrzędnych okreslonych jako liczba całkowita z zakresu od o do m.

  



    



  

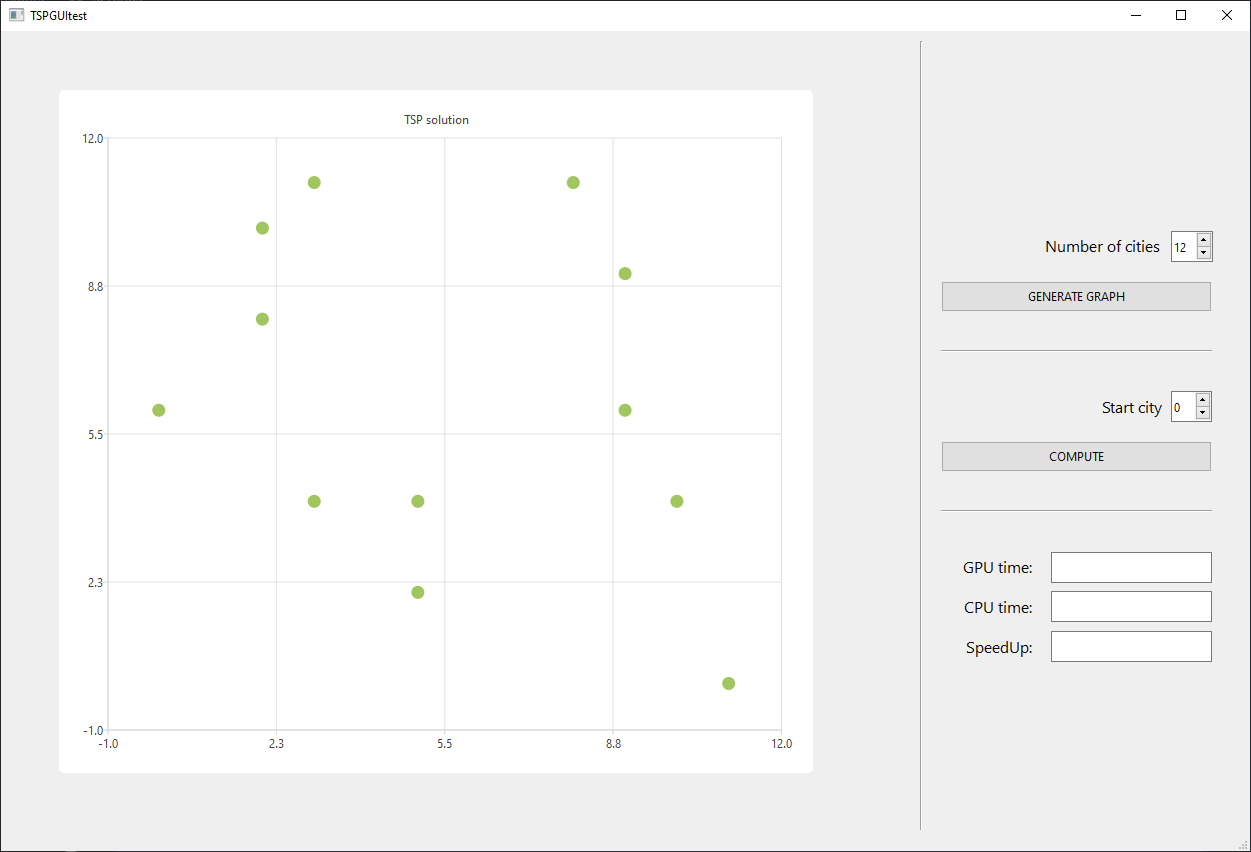
Na podstawie wygenerowanej mapy oraz punktu startowego możemy rozpocząć obliczenia, których rezultat pokazywany jest w formie ścieżki łączącej poszczególne miasta oraz dodatkowo wyświetlana jest informacja o czasach obliczeń dla GPU oraz CPU wraz ze współczynnikiem przyspieszenia.